混合模糊系统的权值参数优化算法
2022-07-23王贵君
陈 雪,王贵君
(1.天津市第六十三中学,天津 300190;2.天津师范大学数学科学学院,天津 300387)
0 引言
模糊系统是输入-输出和状态变量定义在模糊集上的一个非线性映射,其核心是由若干IF-THEN规则所组成的知识库.文献[1-2]利用Stone-Weierstrass定理证明了Mamdani模糊系统的逼近性,并通过叠代分层来简化多个变量的模糊系统内部规则数目.文献[3-4]针对T-S模糊系统引入串联-叠加分层方法给出分层后该系统的输入-输出表达式和计算公式,并侧重于对分层后的T-S模糊系统的逼近性和规则总数进行了研究.文献[5]将Mamdani和T-S模糊系统统一起来建立了广义分层模糊系统,并讨论了分层混合模糊系统的规则数变化和逼近性能.这些结果为Mamdani模糊系统和T-S模糊系统的进一步应用提供了理论基础.
事实上,以往人们主要是对单独的Mamdani模糊系统或T-S模糊系统进行讨论,关注焦点是如何通过不同分层输入方法来缩减模糊规则总数,且分层后的模糊系统须保持逼近性能.文献[6]基于混沌序列和BP算法设计了混沌BP混合算法,从而提高了全局搜索能力及收敛速度;文献[7]提出了一种综合遗传算法和梯度下降法优势的混合遗传算法,以便强化系统的学习能力;文献[8-10]给出了一种在GA算法中融合BP算法的混合学习算法,并以此来实现模糊逻辑系统的自学习,从而达到全局最优和快速搜索.文献[11]基于混合模糊系统通过调控参数重新选取系统参数,证明了该模糊系统对连续可微函数具有逼近性,并且在强化条件下该系统可达二阶逼近精度.然而,该文对混合模糊系统的权值参数优化却并未涉及.本文将基于文献[11]引入的混合模糊系统,通过构造权值梯度向量建立误差函数,进而依据BP算法和遗传算法对梯度向量实施权值参数优化,以便获得全局优化的权值参数优化算法.
1 预备知识
事实上,一般模糊系统是基于知识体系或模糊规则的一类系统,它的本质是由若干模糊IF-THEN规则(简称IF-THEN)所构成的知识库.通常,Mamdani模糊系统和T-S模糊系统是两类常见的系统模型,它们不仅能处理语言信息,而且还能处理数据信息,两者的主要区别是模糊规则的后件输出不同.
Mamdani模糊系统IF-THEN规则形如:
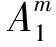
T-S模糊系统IF-THEN规则形如:
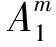
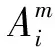
显然,两种模糊系统的IF部分相同,而THEN部分不同.此时,按照各自模糊规则,若采用单点模糊化、乘积推理机和中心平均解模糊化方法,∀x=(x1,x2,…,xd)∈U,得Mamdani模糊系统为
(1)
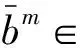
同理,也可获得T-S模糊系统的输出表示为
(2)
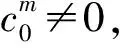
由于Mamdani模糊系统和T-S模糊系统具有相同的IF部分,但又各自具有不同特点,故将二者合并起来建立混合模糊系统是一个重要尝试.实际上,混合模糊系统不仅是原来两种模糊系统的自然推广,而且它还能同时发挥两种系统的各自优势.
2 混合模糊系统及其表示
文献[10]通过引入调控参数λ∈[0,1]将Mamdani模糊系统和T-S模糊系统合并起来建立了一种新混合模糊系统,其混合模糊推理规则形如:
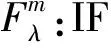
事实上,混合推理规则是通过调控参数λ∈[0,1]将两种模糊系统的THEN部分直接统一,而λ是决定混合模糊系统的一个关键参数.按混合推理规则、单点模糊化、乘积推理机和中心平均解模糊化给出混合模糊系统模型为
(3)
其中:x=(x1,x2,…,xd)∈U⊂d为混合模糊系统的输入变量;调控参数为Mamdani模糊系统中第m个推理规则的输出模糊集Bm的中心;为T-S模糊系统后件线性输出ym的系数;为第m条规则在分量xi处的前件隶属函数;Fλ(x)为混合模糊系统的输出.
特别地,当λ=0时,混合模糊系统(3)退化为Mamdani模糊系统;当调控参数λ=1时,混合模糊系统(3)退化为T-S模糊系统;当调控参数λ∈(0,1)时,正是本文所要讨论的混合模糊系统.
为简单起见,不妨选取前件模糊集为一致完备的三角形模糊数,则∀x=(x1,x2,…,xd)∈U及每个分量xi均满足
此时,由文献[12],公式(3)中分母满足
若令
则∀λ∈[0,1],混合模糊系统(3)可简化为
(4)
3 权值参数优化算法
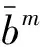
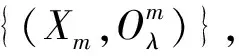
(5)

其中S=(d+2)M,亦即,误差函数Eλ可进一步具体表示为Eλ(W).
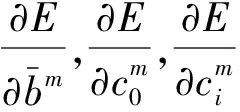
设∇Eλ(W)表示误差函数Eλ(W)的权值梯度向量,则梯度向量∇Eλ(W)也可表示为
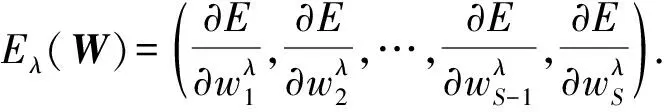
优化算法对任意调控参数λ∈[0,1],先通过输入变量引入动态学习常数与动量常数,获得权值参数的初始解.再采用动态调整交叉概率与变异概率,这样不仅可将BP算法和遗传算法合成,而且也能通过解码转换或搜索得到全局最优解.具体权值参数优化算法步骤如下:

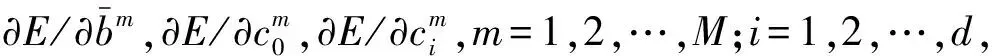
(6)
其中权值参数的差量为
且η[t1],α[t1]分别为学习常数与动量常数.
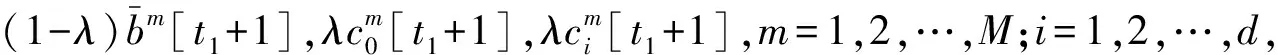
第四步如果‖∇E(W′[0])‖<ε,则输出权值参数向量W′[t1];否则,令t2=t1+1,并转第五步.
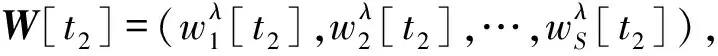
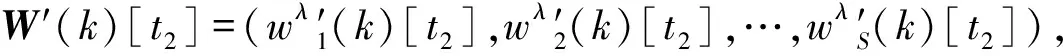

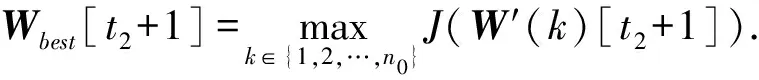
注1 显然,所给算法是依据传统的BP算法和遗传算法的合成所得.所不同的是,该算法是依赖于Mamdani模糊系统和T-S模糊系统合成的混合系统所有调节参数构成的权值梯度向量来依次优化,其中第一至四步隶属于BP算法,第五至八步隶属于遗传算法(GA).这里第四步中范数‖·‖是依据广义欧几里得度量界定,第五步采用二进制编码来表现种群个体更便于解码操作.
4 模拟实例
虽然BP算法具有较好的局部搜索能力,但却存在收敛速度慢和易陷入局部极小点的缺陷.GA算法是基于自然选择与种群进化形成全局寻优算法,它依据编码方式将调节参数转化成遗传空间中个体,并通过解码还原来优化参数,但它源于同一原始群体并非能搜索到全局最优解,甚至出现“近亲繁殖”现象.为克服两种算法的缺陷,本文结合BP算法与GA算法的各自优点对混合模糊系统的权值参数设计优化算法,并由此来提高算法收敛速度.综合所给算法给出流程图(见图1).
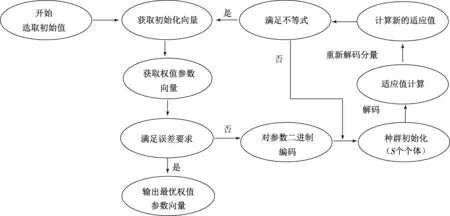
图1 所给算法的权值参数优化流程图
通过一个简单仿真模拟来说明该算法的有效性.为简单起见,选取调控参数λ=0.5来探究混合模糊系统输出的变化.设随机产生1 000组数据,其中前600组数据用于混合模糊系统的训练,后400组数据用于所构建模型的测试.首先,利用权值参数优化算法对混合模糊系统的权值参数进行优化,给定相关参数如下:种群总数n0=40,误差精度ε=0.001,迭代次数T=500,交叉概率设置为0.8,变异概率设置为0.01.按照所给算法的第一至八步得到训练误差图,如图2所示.再利用后400组数据测试该系统的性能,得到测试样本的误差,如图3所示.
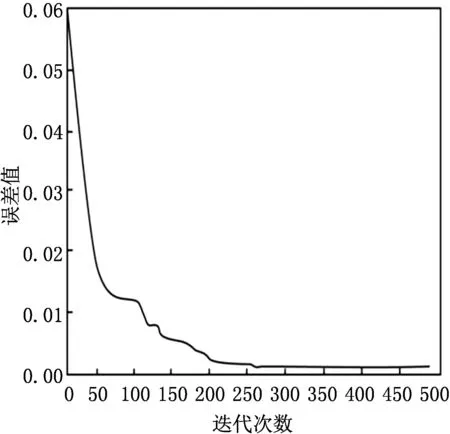
图2 权值参数优化算法训练的误差图
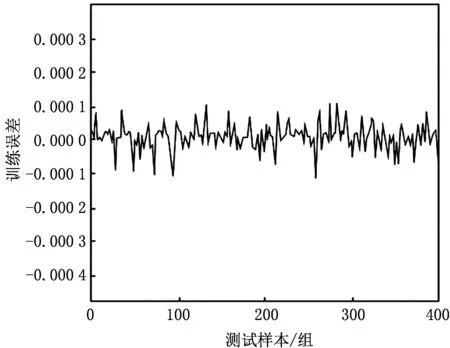
图3 测试样本模型的误差图
由图2看出,本文提出的权值参数优化算法大约经过420次迭代后曲线趋于稳定,混合模糊系统就可搜索到较优的权值参数向量,经测算得误差为8.192×10-4.再由图3知,对于后400组测试数据经测算该混合模糊系统的最大误差为1.093×10-4,平均误差为1.985 4×10-5.经权值参数优化算法后的混合模糊系统虽然有一定误差,但这两个误差在允许误差范围内.另外,改进后的混合模糊系统误差波动范围较小,这不仅在收敛速度上有明显提高,且节省了运行时间,也避免了系统陷入局部极值和随机性的问题.
事实上,所给算法主要对输入变量引入动态学习常数与动量常数,这不仅在加快BP算法搜索速度时达到对混合模糊系统权值参数的优化,而且可将优化后混合模糊系统权值参数作为GA算法的初始种群,进而把原来单个种群进化为多个种群,以便采用动态调整获取交叉概率与变异概率.当然,依据引理1的梯度向量∇E(W),也可通过BP算法与GA算法的相互调用将权值参数按照BP算法进行优化,再通过解码和搜索得到混合模糊系统的全局最优解和优化权值参数.
5 结论
本文基于Mamdani模糊系统和T-S模糊系统合成所建立的混合模糊系统设计了权值参数优化算法,该算法不仅可保证权值参数的全局优化,而且还能克服随机性等问题.仿真结果表明,该权值参数优化算法对混合模糊系统的所有调节参数具有良好的优化性能.此外,调控参数λ的取值对整体混合模糊系统具有重要影响,尤其当λ→0+和λ→1-时,混合模糊系统分别趋于独立的Mamdani模糊系统和T-S模糊系统.因此,如何优化调控参数λ的取值才能使混合模糊系统达到最佳逼近效果也是至关重要的.当然,这正是接下来需要探讨的问题.
