矩阵方程AXB+CYD=E的自反解与反自反解

张四保，邓 勇

(喀什大学数学与统计学院，新疆 喀什 844006)

设P∈n×n.若P*=P且P2=E，则称P为n阶广义反射矩阵.定义n×n如下两个特殊子空间：

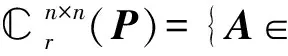
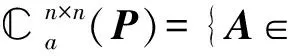
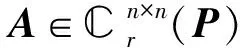
广义反射矩阵P的自反矩阵和反自反矩阵具有许多特殊性质，并被广泛应用到工程和科学计算之中[1].矩阵方程是计算数学领域非常活跃的研究课题之一.关于矩阵方程的解法有大量文献介绍[2-4].

对矩阵方程AXB+CYD=E.

(1)

利用矩阵的广义逆和广义奇异值分解，文献[5-6]给出了其可解条件及通解；文献[7-8]给出了求其自反(反自反)解的几种迭代算法；文献[9]给出了求耦合矩阵方程(1)自反解的梯度迭代算法；文献[10]讨论了受限的广义Sylvester矩阵方程的相容性和通解.自反矩阵和反自反矩阵在信息论、线性系统理论、线性估计理论等领域有着重要的实际应用.本文主要讨论矩阵方程(1)的自反和反自反解.

1 几个主要引理

设P∈n×n是一个广义反射矩阵，于是P可表示为如下形式[11]：

(2)

其中U=[U1，U2]是酉矩阵且U1∈n×r，U2∈n×(n-r).

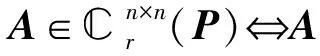
(3)

其中：A1∈r×r，A4∈(n-r)×(n-r)，U和U*如(2)式所示.

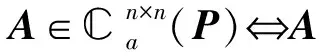
(4)

其中:A2∈r×(n-r)，A3∈(n-r)×r，U和U*如(2)式所示.

不失一般性，假设矩阵A，B，C，D，E∈n×n有如下分解：

(5)

其中：A1，B1，C1，D1，E1∈r×r；A4，B4，C4，D4，E4∈(n-r)×(n-r).

2 主要结果

定理1 给定矩阵A，B，C，D，E∈n×n和n阶广义反射矩阵P，则下列条件等价：

(6)

有解，其中

(7)

(3) 矩阵方程组

(8)

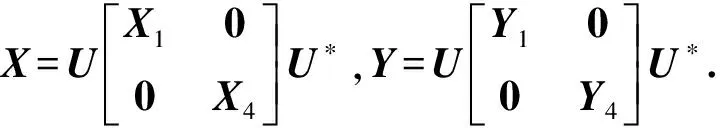
证明(2)⟺(3).将(7)式代入(6)式中，可得矩阵方程组(8).这意味着(2)⟺(3).

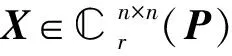
若矩阵方程组(8)有解，则

并且有AXB+CYD=E.

定理2 给定A，B，C，D，E∈n×n和n阶广义反射矩阵P，则下列条件等价：

(9)

有解，其中

(10)

(3) 矩阵方程组

(11)

有解，此时矩阵方程(1)的反自反解可表示为

证明证明过程类似于定理1，此处略去.

3 特殊情况

定理3 给定矩阵A，B，C，D，E∈n×n.若B1=B2=D1=D2=0或A1=A3=C1=C3=0，则下列条件等价：

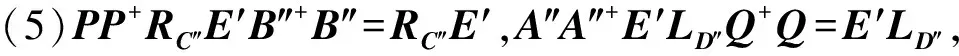
在此情况下，矩阵方程(1)的自反解可表示为

其中：

或

这里X1，Y1，J，J1，V，V1，W，W1，Z，Z1是保持运算的任意矩阵.

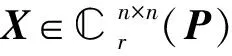
(12)

在此情况下，方程(12)的通解可表示为：

或

其中J，J1，V，V1，W，W1，Z，Z1是保持运算的任意矩阵.

定理4 给定矩阵A，B，C，D，E∈n×n.若B1=B2=D1=D2=0或A2=A4=C2=C4=0，则下列条件等价：

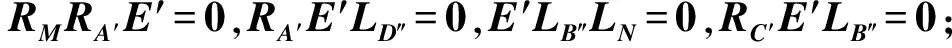
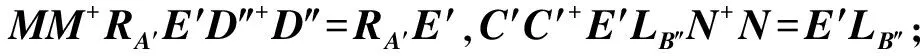
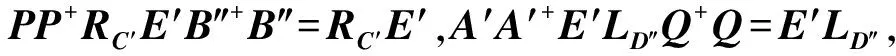
在此情况下，矩阵方程(1)的反自反解可表示为

其中：

或

这里X3，Y3，J，J1，V，V1，W，W1，Z，Z1是保持运算的任意矩阵.

证明证明过程类似于定理3，此处略去.