“数”“形”交错促理解

江苏连云港市灌云经济开发区实验学校（222299）张树伟

在小学数学中，数与形永远是并驾齐驱的，一直贯穿整个教学的始末，这与初中阶段的代数与几何不谋而合。代数的前身就是小学阶段的算术，几何的前身就是小学阶段的平面图形。到了高中、大学阶段，它们就会巧妙融合，衍生出一门新学科——解析几何，用代数知识解决几何问题，可以用函数图像反映数量关系，数与形合二为一，辩证统一，不分彼此。数形结合思想的萌芽就是建立在这样的背景下的，它可以看成是解析几何的萌芽阶段，在小学数学阶段起着至关重要的作用，既是一种重要的数学思想，又是一种解决数学问题的捷径和王牌武器。笔者结合自己的教学实践，谈谈教学中数形结合思想的渗透策略。

一、在数的概念中起步

万事开头难，数形结合思想的渗透最好从识数阶段开始，数域是小学学段的一个重头戏，既是基础，又是贯通全套教材的线索，更是全部数学知识赖以生存的土壤。但对于小学生而言数字的定义是朦胧的，因此，教师不妨借助图形，将可视化的图形与抽象的数字勾连起来，用清晰的图形线条来揭示算术概念中的本质，将抽象的运算转化成直观的图形，从而为学生构筑数学概念的楼宇，夯实地基。

在数学教学中，通过数字与图形的和谐统一和高度对应，引领学生经历构建概念、理解概念及应用概念的全套过程，以感性的图形来证明和诠释理性的概念，学生慢慢从感性材料中脱离表象，在思维深处建立抽象概念，这样的理性概念可谓根基浑厚。

如在教学“分数的初步认识”一课时，教师可借助各种各样的感性材料来揭示分数的内涵，从而让学生直观感知分数的存在与用途。

教师在设计情境时，用符号来深入刻画“一半”的意义。可以选用图形符号，也可以选用文字符号，还可以选用特殊字符，如等，在比较与商议中凸显符号的长处：简明 扼 要 、 形象直观，胜过千言万语。与此同时，也要让学生学会使用图形语言去表达分数。

在诠释分数概念之后，讲述符号背后的分数发展史，让学生接受数学历史文化的熏陶，充分感受分数的发展脉络。可以将各个历史阶段分数的表示法陈列出来，比如中国、埃及的先民们，都各自有独特的分数表示法（如图1），可惜这些表示法最终没有流传下来，直到人们发明了分隔符号“—”，这种表示法才算正式“落地”，并保留至今。最后，人们统一国际标准、创立数轴模型，在数轴上的整数坐标之间安插分数坐标。

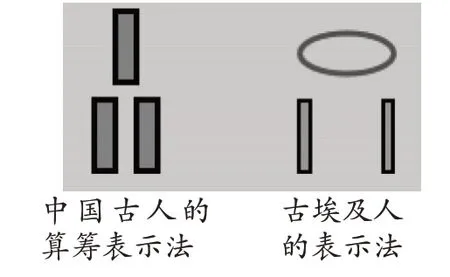
图1

除了借用这种半数半图的形式深刻揭示分数的含义，教师还可以为学生的理解途径和渠道提供形形色色的材料，将分数与整数统合到一条数轴上，帮助学生在完备的数域中捉摸分数的地位。

在整个小学阶段，许多数域（如小数、百分数等）的概念教学，教师都要精心设计，谋篇布局、通盘考虑，利用图形的直观优势，让“形”成为最佳的佐证材料，将“数”的来源和本质阐释清楚，打通图形与数字之间的壁垒，也让“形”成为学生思维向更高处攀升的跳板，学生对数字概念的认知自然会从浅薄走向深邃。

二、在数的运算中加速

在算术教学中，将算法背后的算理推向前台，直接呈现在学生面前，让学生在学习算法时不得不重视算理，应该成为教师教学的一大风向。教师应该用心在算术教学中渗透数形结合思想，用一些形象直观的图形，清楚地演绎出算理，帮助学生借助图形促进思维快速发展，以图形促进数字运算的可感可触，从而实现由算理到算法的“反哺”。

如在教学“两位数加两位数的进位加法”时，教师应该先指导学生摆小棒，尝试计算19+18，再如图2所示，结合小棒合并的直观图，一边对照小棒数量一边抽象出数字，利用小棒的捆数和竖式的对应性（1捆对应十位数字1，1根对应个位数字1），推演竖式计算的过程和原理，用摆小棒与列竖式“双线并行”的方法演绎“满十进1”的深刻道理。在这里，直观操作是为了攻克计算时的思维障碍和理解难点。

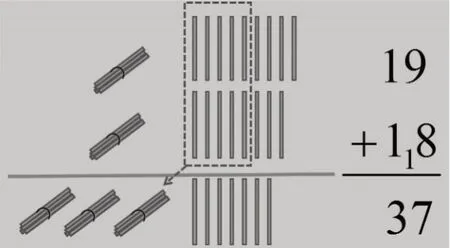
图2

在操作后，学生慢慢就会不依靠小棒，抽象出纯数字计算的整个流程。而在后续的教学中，直观图并没有失去利用价值，仍可以发挥余热，学生可以回顾学习经历，利用直观图来反思整个数字计算过程，为竖式计算的每一步追根溯源，看看每一步计算的来源，为每一步的运算找到原型和“母体”，为数字竖式计算找到与直观图形这一“母体”维系关系的“基因”。

因为竖式计算中的每一步都能找到它在直观图形中的“基因片段”，所以学生能轻易地理解并接受“满十进1”的合理性和必要性，实现算理与算法的高度统一。

又如在教学“分数乘、除法”的知识时，教师可以使用矩形塑料片作为直观材料，让学生通过分块、涂画的手工操作，将“数”的运算变换为对“形”的裁剪取舍，从而借助图形语言来认识并掌握分数乘、除法的算理。将数形结合的思想融入数学运算中，为图形和数字找到新的契合点，将算法的本质揭露无遗，为算理和算法齐头并进、水乳交融增添新料。

三、在解题中起飞

1.用数形结合化复杂为简单，厘清数量关系

数量关系是一切算式的存在基础，没有数量关系的数字就不可能存在于同一个算式中。课程标准指出，要从现实生活或具体情境中抽象出数量关系。数量关系不是凭空产生的，而是源于生活实际，缺少了现实生活情境支撑的数量关系就是空中楼阁，对一些应用题，分析其中数量关系反而成了重点和难点，列式计算倒是其次，因其数量关系繁多庞杂，学生很难全面掌握，想一个个记忆，更是难如登天。

如果充分运用数形结合思想，就会事半功倍，特别是巧妙运用线段图等直观地呈现各种复杂、不同类别的数量关系，更是起到快刀斩乱麻的作用，线段图就像是一把破解数量关系的万能钥匙。

如解决“快餐店、电玩城和数码城在香港路的同一边。快餐店距数码城280米，电玩城距数码城350米。快餐店距电玩城多少米？”这一问题时，大部分学生只会一根筋地认为快餐店与电玩城分别在数码城两侧，列式为280+350=630（米）。教师如果能引导学生用线段图来表示三者的位置关系，就会引起学生警觉：快餐店、电玩城和数码城各在什么位置呢？用线段图就能清楚、直观地展示两种可能，如图3。

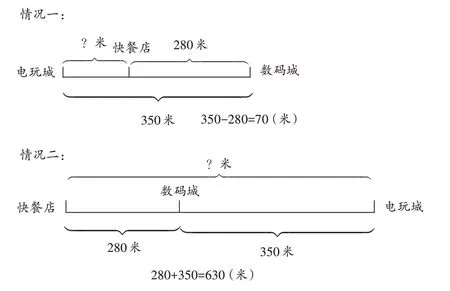
图3

直观的线段图不但可以激发学生的浓厚兴趣，还可以让复杂的关系变明朗，让抽象的问题变得形象具体，帮助学生从对比强烈、泾渭分明的线段图中提炼数量关系，建立基本的数学模型，提高解决问题的效率。

2.用数形结合化抽象为直观，巧解经典

如鸡兔同笼问题“已知鸡和兔一共有10只，一共有32条腿，求鸡和兔各有几只？”这类问题，传统解法林林总总，列方程解答、枚举法、假设法。方法虽多，但对于小学生来说却感觉处处受限、处处掣肘。比如中低学段的学生，对方程一无所知，用列举法容易挂一漏万、丢三落四，假设法的数量关系十分抽象，而且存在多种变化，虚实交错，真假难辨，弄得学生晕头转向，不知哪个条件是真实的，哪个条件是假设的。

那么，采用什么办法能够让低年级学生也能参透这个经典难题呢？答案就在眼前，非数形结合莫属。

如图4，先用圆圈表示10只动物。假设这10只动物全是鸡，那么每只鸡有2条腿，把腿补齐，只有20条腿，和总腿数相比，显然还有32-20=12（条）腿没着落。如果每只鸡再增加2条腿，这样一来就有12÷2=6（只）鸡需要“多长”2条腿，显然这是不可能的，那么只有6只鸡变成兔子，才能多出12条腿，于是得出兔子有6只，鸡有4只。

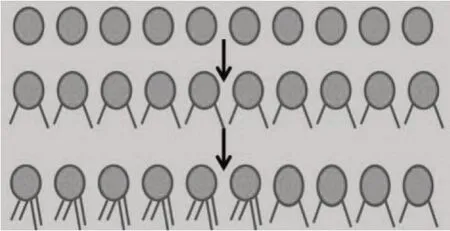
图4

在类似的教学中，都可以让学生按照题意画图，通过直观图将抽象的算术问题直观化，这种做法看似小儿科，其实迎合了儿童心理，因为小学生此时正处于动作运算阶段向逻辑运算阶段跃升的发育期，采用这种途径不但让问题变得简单，而且保护了学生的自信心。

四、在创新思索中发展

数形结合思想是小学数学中最常见的思想方法之一，也是学生最喜爱的数学思想方法之一。因为它符合儿童的思维特点，以形象、具体为主，以直观为核心。因此，在小学数学教学中教师要在数的概念建立、数的运算学习、问题的解决研究中等灵活使用数形结合思想，还要在学习创新、创新思考等层面做出必要的努力，以期通过数形结合思想方法的应用，让学生的数学学习变得更具智慧、更有深度。

以数学问题“林虹水果超市近期购进苹果120箱，比购进的橘子的3倍少15箱。问购进橘子多少箱？”的教学为例。

1.放手一试，发现端倪

首先采取放手策略，让学生在自主思考的前提下进行尝试。教学中教师切忌急躁，要给学生一个读懂问题信息、分析思考问题的机会，更要给他们一个自我体验的机会。

学生纷纷投入问题的研读和分析之中，并按照自己的思考进行解读。有学生提出：因为苹果的箱数与橘子箱数的3倍有关，所以就有120÷3=40（箱），再用40+15，得结果是55箱。也有学生提出新的思路：应该是120×3-15，结果是345箱，这样的思考才符合题意。

其次，引导学生对不同思考进行必要的甄别。随着不同结论的出现，学生也会惊讶无比。此时，就有学生提出疑问：同样的一个问题，为什么不同的思考会出现不一样的结果呢？这是没有道理的。疑问给学生以震撼，也诱使学生深思问题研究中的滋味。

2.运用方法，助力思考

有学生提出：可以用结论去验证，看看是不是有正确的结果。随着这个思路，学生便开始验算。在验算中学生发现，对于答案55箱，结合习题的关键点“比购进的橘子的3倍少15箱”，验算发现，55×3-15=150（箱），不符合习题中的信息“120箱”，它是错误的。再验算345箱，345×3-15，无须计算下去，一眼就能看出这个答案多么滑稽。

面对此情景，教师就得引导学生开动脑筋，寻找记忆中的方法策略。此时，画图策略就会被提出。紧接着，学生就积极参与到画线段图来研究问题的学习之中。经过一段时间的画图，以及对图例的解读，学生发现：120箱比橘子箱数的3倍少15箱，因此补上15箱后的数量正好是橘子箱数的3倍，得120+15=135（箱），135÷3=45（箱）。随着验算的开展，他们发现这个思考是可靠的。

就在此时，也有学生提出：看线段图，可以把120箱平均分成3份，每份40箱，还要把少的那15箱也平均分成3份，每份5箱，把它们合起来也是45箱。话音一落，课堂就掀起一片争论声，随着思考和争辩的推进，学生终于发现这一思考也是有道理的。由此，创新思考的“种子”就会在学生的脑海中埋下。

总之，在小学数学教学中，教师应有意识地渗透数形结合思想，以“形”的直观弥补“数”的抽象，以“数”的准确反哺“形”的粗略，变抽象为具体，化无形为有形，实现代数与几何两大数学分支的早期融合。