电网频率小扰动下虚拟同步发电机统一模型关键参数辨识
2022-07-22曲玉博刘鹏辉郭向伟杜少通
朱 军 曲玉博 刘鹏辉 郭向伟 杜少通
电网频率小扰动下虚拟同步发电机统一模型关键参数辨识
朱 军 曲玉博 刘鹏辉 郭向伟 杜少通
(河南理工大学电气工程与自动化学院,河南 焦作 454003)
针对并网逆变器的虚拟同步发电机控制策略多样化,建立统一的虚拟同步发电机线性化模型,提出逆变器实际输出等效惯量和阻尼系数的辨识方法,量化其对电网的支撑能力。从电网频率扰动的角度出发,同时考虑逆变器采样环节的锁相环与滤波器的影响,建立能够表征虚拟同步发电机动静态调节性能的小信号统一模型。根据所建立的模型,利用零极点法分析控制参数对系统的影响,采用电网频率扰动与负荷扰动激励出系统功率动态信息,基于多新息理论的随机梯度法辨识出逆变器输出等效惯量和阻尼系数。最后搭建系统仿真模型,验证分析及辨识方法的正确性和有效性。
虚拟同步发电机(VSG);统一模型;等效阻尼;等效惯量;参数辨识
0 引言
光伏、风电等新能源发电依靠并网逆变器并入电网,这些电力电子逆变器设备具有控制灵活、响应速度快的优点,但是随着电力系统中电力电子设备的增多,这些装置本身低惯量无阻尼的特点会对电力系统的稳定运行造成影响。虚拟同步发电机(virtual synchronous generator, VSG)技术是利用控制算法模拟同步发电机的模型,使逆变器具有阻尼与惯量特性,能够在电网频率、电压发生波动时主动参与系统的调频调压服务,改善系统的运行状态。VSG的提出为提高电网对新能源的消纳能力提供了新思路。
VSG概念最早由荷兰学者在“VSYNC”项目中提出[1],随后学者们针对VSG开展了不同的研究。文献[2]介绍了VSG的原理、拓扑、应用及存在的问题,对理解VSG技术具有很好的参考意义。文献[3]梳理了采用虚拟惯量和阻尼的各种控制技术,讨论了惯量与阻尼技术存在的问题及未来研究思路。文献[4-6]介绍了光伏VSG技术,分析VSG在光伏逆变器中的调频调压等功能,以及在光储微电网应用中的一些问题。文献[7]将VSG与转子交角下垂控制结合,并加入虚拟电抗解决逆变器电压利用率过低的问题,同时证明虚拟电抗的加入对有功功率分配的影响不大。文献[8]分析功率耦合机理,提出采用d轴电流表征功率耦合,通过在d轴电流加入补偿环节来补偿无功功率实现功率解耦。
VSG的参数设置直接影响系统的稳定性,而VSG的主要参数阻尼与惯量虽然是给定的,但经过一系列的信号采集、变换等控制后,系统输出的阻尼与惯量是否符合设定值尚未可知。因此,需要对VSG实际输出阻尼与惯量进行参数辨识。文献[9]建立VSG控制输出功率与指令功率的二阶模型,然后利用递推二乘法辨识出VSG输出的惯量及阻尼参数。文献[10]推导了VSG在离网、并网模式不同状态下的响应,采用曲线拟合的方法设计了一种互为验证的VSG参数辨识方法。文献[11]建立下垂控制和VSG控制的统一线性化模型,然后使用零阶保持器将系统无差离散化,并用智能算法辨识出VSG参数。
上述VSG参数辨识方法都是针对某一特定的VSG模型进行辨识,由于VSG模型的建立方法不统一,在面对不同VSG结构或VSG结构未知时则无法辨识。针对此问题,本文从实际电网频率频繁波动的角度考虑,采用电网频率扰动,并考虑逆变器采集电网频率时需要锁相环(phase locked loop, PLL),以及功率计算需要的滤波环节,建立完整的VSG控制小信号模型。然后通过系统的闭环零极点分析锁相环与滤波环节对系统性能的影响,将VSG模型分为降阶模型和全阶模型。通过电网频率扰动与负荷扰动实验,结合多新息随机梯度法,推导出统一模型VSG的关键参数辨识方法,定量辨识出采用VSG控制的逆变器实际输出的等效阻尼和惯量,量化其对电网的支撑作用,也可作为商用VSG控制逆变器的检验手段。
1 VSG基本原理
VSG技术是将同步发电机的转子运动方程引入逆变器的控制算法中,借助储能技术使逆变器也具有像同步发电机一样的调压调频能力。VSG技术主要包括主电路及控制算法部分,如图1所示。主电路包括新能源电源、储能系统、逆变器、滤波电路;控制算法部分包括功率控制环、电压电流控制环及正弦脉宽调制(SPWM)。

图1 VSG主电路及控制算法部分
由图1可知,采用VSG控制的逆变器包含电压电流环控制、VSG控制算法、滤波电路及线路阻抗。文献[12]建立了包含VSG控制算法、滤波电路及线路阻抗、电压电流环控制在内的逆变器完整小信号状态空间模型。通过对特征根的分析可知,滤波电路及输电线路等参数主要影响系统的高频段特征根,系统的频率响应则分布在低频段,主要受VSG功率控制环的影响,而电压电流环控制响应时间远快于系统频率响应,故VSG模型可忽略电压电流环、滤波电路及线路阻抗的影响,只考虑功率环。
由于逆变器提供的阻尼与惯量只与功频控制环节有关,与无功环无关,故本文只研究有功控制环节。有功控制部分包含虚拟调速器与转子运动方程的模拟,而由于建模方法选取的不同,虚拟调速器与转子运动方程的模拟方式也不同。如转子运动方程的阻尼转矩参考角频率采用电网角频率g[13],此时阻尼转矩参与系统动态调节过程;参考角频率采用额定角频率0[14],此时阻尼转矩参与动态与稳态调节过程。调速器同理,参考角频率可选取电网角频率g或额定角频率0,这就使VSG的建模多样化。为使VSG的参数辨识具有一般性,需建立统一的VSG模型以表征所有结构确定的VSG控制策略。在此基础上,将虚拟调速器的有功下垂系数分为动态和稳态有功下垂系数,分别控制其动态及稳态调节性能,建立统一的VSG控制模型。虚拟调速器及转子运动方程模拟方式为


考虑到电网角频率的测量需要锁相环环节,以及功率采集时避免波形较粗无法利用而需要的滤波器环节,得到电网角频率与输出功率为

式中:e为逆变器输出功率;PLL为PLL环节传递函数;t为滤波器传递函数。
由图1可计算得逆变器输出功率为
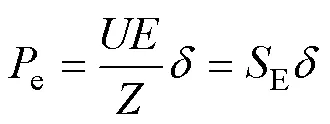
式中:、为电网电压和VSG输出电压;为逆变器输出阻抗;E为VSG功角与有功功率的增益。
参数辨识环节需要对系统施加一个扰动激励出系统的动态变化,由于VSG的惯量和阻尼是在频率波动时稳定系统频率、功率,因此选择模拟电网的频率波动,对电网频率施加扰动。将式(1)~式(3)线性化可得到计及功频控制环节、滤波环节、PLL环节的VSG控制模型,系统输出功率与电网角频率之间的传递函数为

式中:d=10+1,为等效动态阻尼系数,控制VSG的动态调节性能;s=20+2,为等效稳态阻尼系数,控制VSG的稳态调节性能。
功率环节的滤波器采用一阶低通滤波器,电网频率采集的锁相环采用同步旋转坐标系锁相环,其传递函数分别为
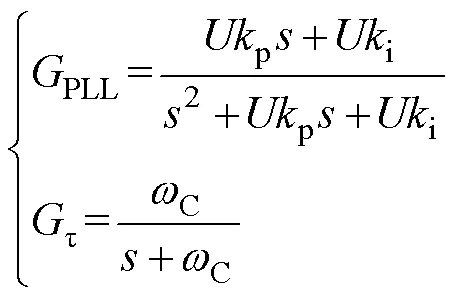
式中:C为滤波器截止频率;p为比例系数;i为积分系数。
结合式(4)和式(5)可知,由于一阶低通滤波器及PLL环节的加入,使系统从一个二阶系统升为五阶系统,辨识难度大大增加。
2 VSG模型分析
由第1节分析可知,PLL及滤波器的加入使系统模型升阶,增加了辨识的难度,由此,首先分析PLL及滤波器对系统性能的影响。
PLL传递函数PLL为二阶系统,对比二阶系统的标准形式得到其阻尼比及自然振荡频率n为

在控制系统中,为使系统具有较好的动态性能,二阶系统一般设置阻尼比=0.4~0.8[15],这里取=0.707,n设置为1~50Hz;为了使输出功率经过滤波后尽量减少谐波,同时避免功率滤波后波形失真,C设置为20~200Hz。联合式(4)和式(5),得到VSG控制包含PLL及低通滤波器在内的完整五阶模型如式(7)所示,画出其零极点分布如图2所示。

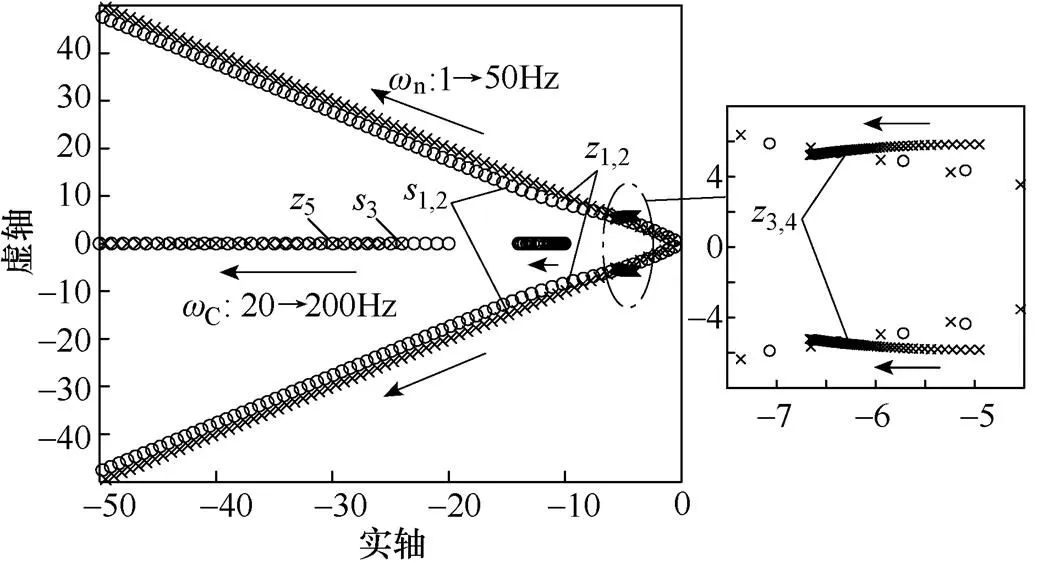
图2 含滤波器和锁相环的VSG零极点分布
由图2可知,滤波器参数C影响极点3,4、5和零点3,由于实轴上的零极点对系统阻尼的影响是随其靠近坐标原点的程度决定,越靠近坐标原点,对系统阻尼影响越大,因此极点5和零点3对系统阻尼的影响较小,可以忽略。由主导极点分析法可知,主导极点选取为最靠近虚轴而附近没有闭环零点的极点,极点1,2和零点1,2构成了一对偶极子,这对偶极子随着n的增大而逐渐远离虚轴,此时极点3,4就成为主导极点。而极点3,4受参数C的影响在靠近虚轴附近小范围内变动,C并没有改变其主导极点的地位,即C对其影响较小。
综合分析,滤波环节C参数对系统性能的影响较小,可以忽略。略去滤波器环节后系统模型变为

求出其闭环极点如式(9)所示,并画出其零极点分布如图3所示。


图3 只含锁相环的VSG零极点分布
由图3可知,极点3,4在省去滤波环节影响后仍为主导极点,验证了前文分析的正确性,其位置主要由功率参数、d、s决定,即系统的稳定性主要由参数、d、s决定。而偶极子1,2、1,2随n的增大逐渐远离虚轴,当其距离虚轴的距离超过主导极点的3~6倍以上时[15],即可忽略其影响,即PLL参数满足式(10)时,PLL环节可以忽略。
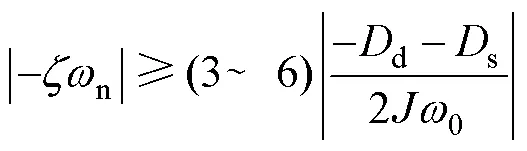
此外,从控制系统的响应角度分析,PLL影响了电网角频率的测量,使角频率原本的线性过程经过PLL环节变成了二阶系统的响应过程,而当二阶系统的阻尼比确定时,系统调节时间由自然振荡角频率n决定,n越大,调节时间越短,快速性越好,对电网角频率测量的影响就越小。
综合上述分析,滤波环节和PLL环节在满足要求时都可以省去,此时,记t=1、PLL=1,系统模型降为如式(11)的二阶系统。
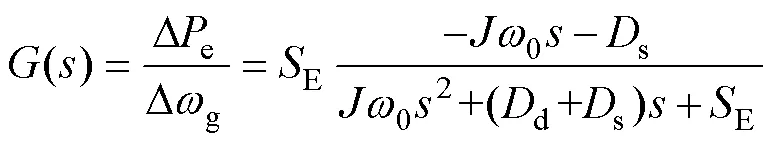
3 多新息随机梯度法VSG关键参数辨识
在前文建立的VSG模型基础上,参数辨识还需获得系统输入输出数据并确立等价准则。输入输出数据通过对电网频率施加扰动,激励出系统的功率动态过程而获得;等价准则即误差函数,是用来衡量模型与实际过程的接近程度。本文按照系统实际输出功率与辨识模型输出功率的误差建立准则函数如式(12)所示,令准则函数达到最小,即辨识模型与实际过程最接近,此时的参数估计即为所求。
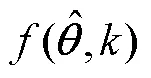
将准则函数极小化的过程即为参数优化过程,本文利用多新息理论结合随机梯度法的多新息随机梯度法进行参数优化。随机梯度法计算速度较快,多新息理论则能动态地利用观测数据,提高数据的利用率,同时加入加权值来调整当前时刻数据占的比重,具有较好的辨识精度。前文已经得出采用VSG控制的逆变器模型由于PLL及一阶低通滤波器的影响,系统模型分为降阶和全阶两种,下文分别考虑两种情况下的参数辨识。
3.1 VSG降阶模型参数辨识算法
当PLL参数满足式(10)时,则PLL=1,同时t=1,系统降为二阶系统,将其化简后得

其中

将其转化到离散域为

式中,为仿真周期。
则辨识模型输出为
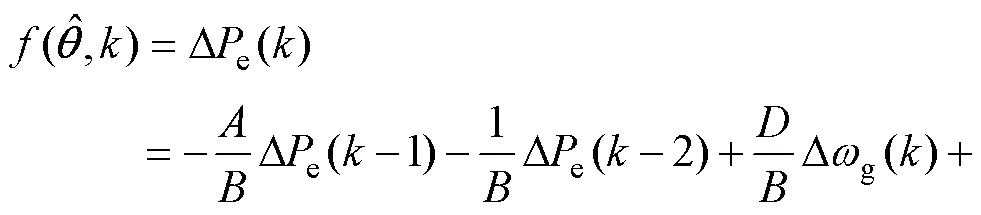

其中

将式(16)代入式(12)得到VSG模型参数辨识的误差函数,基于负梯度搜索原理推导出引入加权因子的多新息随机梯度法(weighted multi-new interest stochastic gradient method, WMISG)的VSG参数辨识算法为
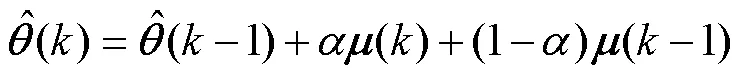




式中:为新息长度;为加权因子,用来控制当前时刻的修正项。
利用WMISG辨识VSG关键参数的步骤如下:
1)给定电网频率一个小扰动,激励出系统动态变化,收集输出功率数据()及电网频率数据g(),数据长度为。

5)令=+1,返回步骤3),直到=,辨识结束。
3.2 VSG全阶模型参数辨识算法
在并网模式下,当PLL参数不满足式(10)时,PLL的影响不能忽略,由于电网频率经过测量后为


其中
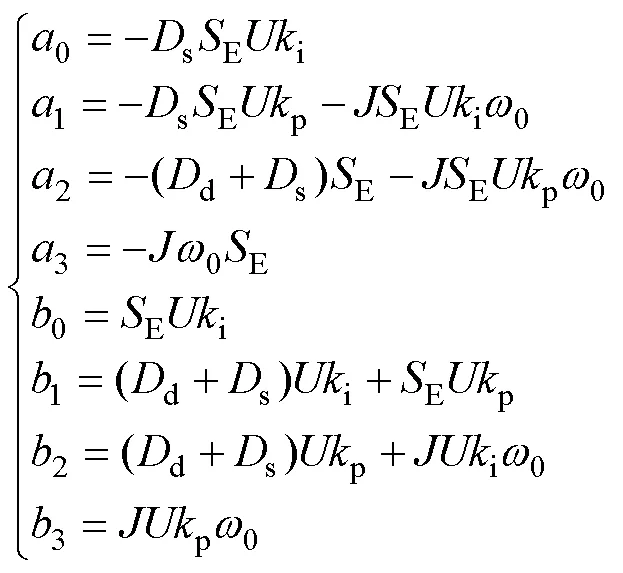
式(23)即为VSG系统的全阶模型,可对其进行分步辨识,首先进行VSG离网模式下的负荷扰动实验,辨识出系统的等效阻尼系数;再进行VSG并网模式下电网频率扰动实验,模拟并网模式下电网频率发生扰动的情况,辨识出系统的惯量。
1)负荷扰动参数辨识方法
逆变器离网模式下,令电网角频率g等于额定角频率0,此时系统的模型变为

式中,zds,为总等效阻尼系数。
由终值定理可得离网模式下VSG的稳态响应为

因此,VSG系统总等效阻尼系数为

由式(27)可知,离网模式下VSG控制在稳态时的输出功率变化量与系统角频率变化量的比值等于VSG的总等效阻尼系数。故通过VSG在离网模式下的甩负荷试验,测得其稳态时的输出功率数据与角频率数据,即可测得VSG的总等效阻尼系数。
2)并网频率扰动参数辨识算法
将式(23)VSG模型离散化后得

则其辨识模型输出为

其中

同样,运用3.1节所推导的WMISG对式(23)进行辨识,即可求出系统输出的动态、静态阻尼系数与虚拟惯量。其中,

4 仿真分析
4.1 VSG降阶模型参数辨识仿真
当VSG系统中不存在PLL或PLL参数满足式(10)而可以被忽略时,系统模型降为二阶系统。首先,在Matlab/Simulink中搭建如图1所示的系统,仿真参数设置见表1。

表1 仿真参数
首先对电网频率施加扰动激励输出系统动态过程。我国规定正常运行情况下的电网频率允许偏差为±0.2Hz,在仿真0.2s时对电网频率施加-0.1Hz的扰动,在2s时施加+0.1Hz的扰动,仿真时长4s,采样周期设置为10-5s。激励出系统的动态变化,测得VSG输出功率数据及电网角频率变化数据。其中PLL参数设置为n=100Hz,=0.707,即p=0.454 7,i=32.154 3,满足式(10)要求。图4为逆变器输出功率与电网角频率变化波形。

图4 逆变器输出结果
将测得的VSG输出功率与电网角频率数据代入辨识算法中,设置新息长度=3,则得到系统的辨识模型如式(32)所示,辨识得到系统d=2 889p,s=14 505p,=15.78kg·m2,辨识误差分别为3.7%、3.3%、5.2%。系统的辨识模型输出功率与实际输出功率对比如图5所示。

4.2 VSG全阶模型参数辨识仿真
首先进行VSG离网模式下的负荷扰动实验,参数设置见表1。初始设置逆变器带2kW负荷运行,在2s时切除1kW负荷,仿真时长4s,采样周期10-5s,角频率变化如图6所示。
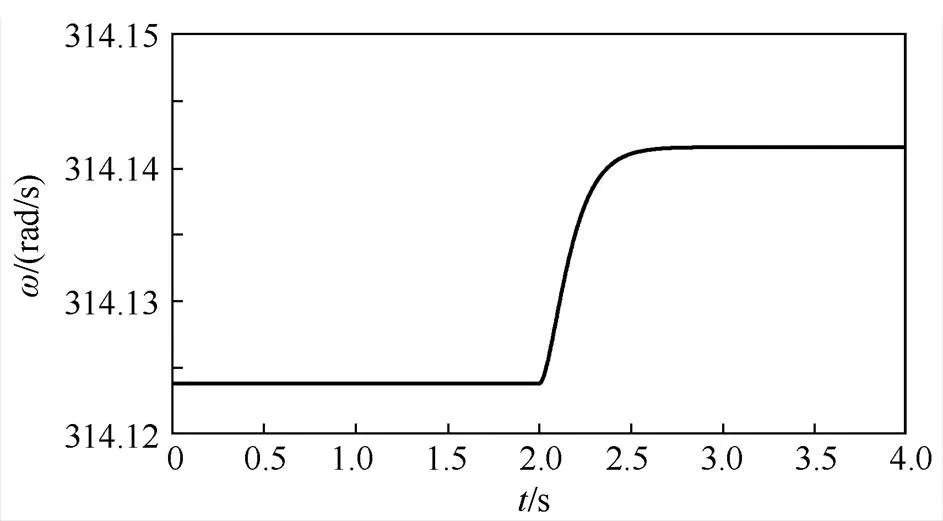
图6 VSG输出角频率变化
由式(27)可得,系统总等效阻尼系数z=s+d=-D/D,其中D=1 000W,为使D数据具有一般性,分别采集角频率在1~2s及3~4s时的数据取平均值后再作差,得到D=-0.018 52rad/s,则总等效阻尼系数z=53 995.73=17 187p。
进行并网模式电网频率扰动参数辨识实验前,首先验证PLL参数对系统性能的影响及式(10)的正确性,分别设置不同的PLL参数,对比PLL参数不同时对系统输出功率的影响,以及对电网角频率测量的影响。PLL参数设置见表2,对比结果如图7所示。
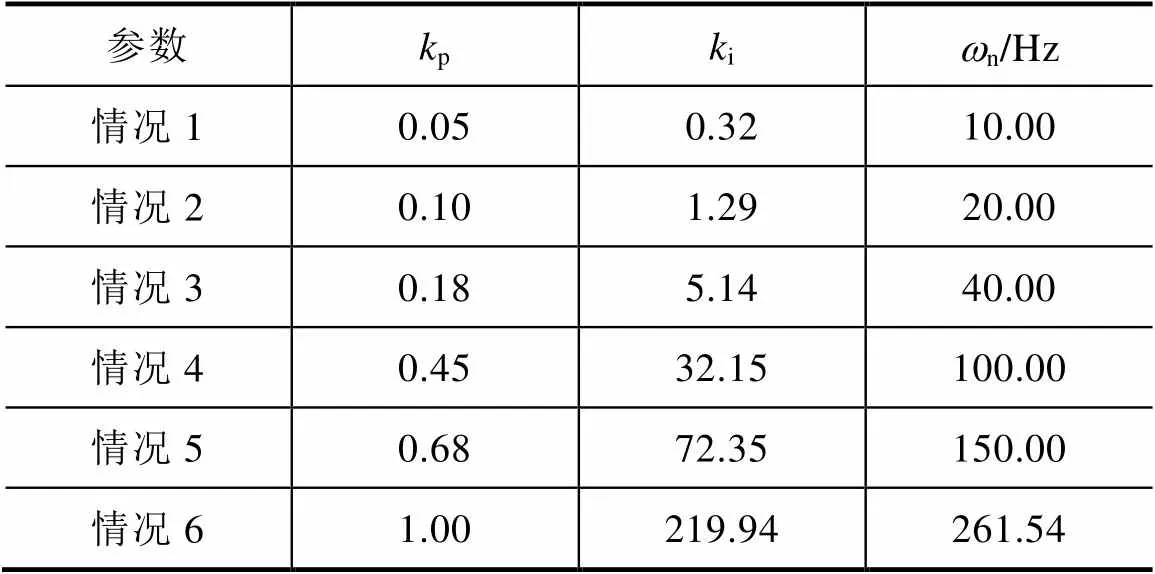
表2 PLL参数设置
从图7(a)可以看出,随着n的增大,PLL对电网角频率的影响过程越来越快。从图7(b)可以看出,当n参数较小,不满足式(10)时,系统输出功率曲线为1、2、3,峰值变化较大;当n满足式(10)时,输出功率曲线为4、5、6,输出功率几乎没有差异,验证了上述PLL对系统性能影响分析的正确性,即当PLL参数满足式(10)时,对系统输出功率的影响较小,可以忽略。

图7 PLL参数不同时VSG输出功率和电网角频率
经过上述分析与验证可知,滤波器环节对系统影响较小,可以略去。通过VSG离网实验估算PLL参数满足式(10)时,可以使用VSG降阶模型进行辨识;否则直接使用VSG全阶模型进行辨识。
VSG全阶模型参数辨识,电网频率扰动方法同上,采集输出功率及电网角频率变化数据,其中PLL参数设置为p=0.1,i=1.3,将仿真测得数据代入WMISG,得到参数辨识结果见表3。

表3 辨识结果
由表3可以看出,d的参数辨识结果与设定值误差较大,由第2节分析与PLL参数仿真验证可知,这是由于PLL本身为二阶系统,它在测量电网角频率时也产生了惯量和阻尼,当其自然振荡角频率较小时,响应过程变得缓慢从而把自身的惯量和阻尼叠加到整个系统中,而动态阻尼系数d则控制VSG在动态调节过程的阻尼,由图7(b)可知,曲线1、2在动态过程中的超调量较大,阻尼能力较弱,满足前述分析。因此,VSG参数辨识的结果实际上是包含PLL等影响在内的等效惯量和阻尼,即整个逆变器实际输出的等效惯量和阻尼。
上述仿真实验结果表明,本文所提的VSG模型能够正确表示VSG控制策略,VSG参数辨识方法能准确辨识出VSG等效惯量与阻尼。
5 结论
本文通过分析不同的VSG建模方法,基于电网的频率扰动建立了VSG的统一线性化模型,能够表征VSG的动态与静态调节性能,采用多新息随机梯度法定量辨识出逆变器输出的等效惯量与阻尼,在面对结构不同或未知的VSG时也能适用。仿真验证了模型及辨识方法的可行性,得到主要结论如下:
1)逆变器输出的惯量与阻尼不只是VSG中设定的惯量、阻尼,而是系统各控制环节叠加影响后的等效惯量与阻尼。
2)滤波器与锁相环参数设置适当时,其对系统的影响过程在短时间内完成,反馈不到系统的输出功率环上,此时可完成VSG模型的降阶。但当参数或结构未知时,可直接使用全阶模型进行辨识。
3)通过电网的频率扰动结合离网模式的负荷扰动获得系统动态过程数据,采用多新息随机梯度法进行参数辨识,数据利用率高,辨识算法简单有效,可准确识别出逆变器输出的等效阻尼与惯量大小,量化逆变器对电网的支撑作用。
[1] VISSCHER K, DE HAAN S W H. Virtual synchronous machines (VSGs) for frequency stabilisation in future grids with a significant share of decentralized gen- eration[C]//CIRED Seminar 2008: SmartGrids for Distribution, Frankfurt, 2008.
[2] CHEEMA K M. A comprehensive review of virtual synchronous generator[J]. International Journal of Electrical Power & Energy Systems, 2020, 120: 106006.
[3] 赵恩盛, 韩杨, 周思宇, 等. 微电网惯量与阻尼模拟技术综述及展望[J]. 中国电机工程学报, 2022, 42(4): 1413-1427.
[4] 高海力, 谭建成. 大型光储联合虚拟同步发电机技术综述[J]. 电气技术, 2018, 19(1): 1-4, 9.
[5] 陈文倩, 辛小南, 程志平. 基于虚拟同步发电机的光储并网发电控制技术[J]. 电工技术学报, 2018, 33(增刊2): 538-545.
[6] 陶银正, 蒲道杰, 毛福斌. 虚拟同步发电机技术及其在光储微电网中的应用[J]. 电气技术, 2016, 17(11): 36-40.
[7] 伍兴煌, 魏强. 使用虚拟阻抗的虚拟同步机转子角下垂控制[J]. 电气技术, 2020, 21(3): 31-36, 58.
[8] 姜静雅, 王玮, 吴学智, 等. 基于自适应无功功率补偿的虚拟同步机功率解耦策略[J]. 电工技术学报, 2020, 35(13): 2747-2756.
[9] 罗琴琴, 苏建徽, 林志光, 等. 基于递推最小二乘法的虚拟同步发电机参数辨识方法[J]. 电力系统自动化, 2019, 43(1): 215-221.
[10] 颜湘武, 王俣珂, 贾焦心, 等. 基于非线性最小二乘曲线拟合的虚拟同步发电机惯量与阻尼系数测量方法[J]. 电工技术学报, 2019, 34(7): 1516-1526.
[11] 于鸿儒, 苏建徽, 徐华电, 等. 并网逆变器虚拟惯性与阻尼的等效及辨识[J]. 中国电机工程学报, 2019, 39(20): 6034-6043, 6184.
[12] 曾德银, 姚骏, 张田, 等. 虚拟同步发电机多机并联系统的频率小信号稳定性分析研究[J]. 中国电机工程学报, 2020, 40(7): 2048-2061, 2385.
[13] 马铱林, 杨欢, 屈子森, 等. 改善虚拟同步发电机阻尼特性的设计方法[J]. 电网技术, 2021, 45(1): 269-275.
[14] 杨赟, 梅飞, 张宸宇, 等. 虚拟同步发电机转动惯量和阻尼系数协同自适应控制策略[J]. 电力自动化设备, 2019, 39(3): 125-131.
[15] 胡寿松. 自动控制原理[M]. 5版. 北京: 科学出版社, 2007.
Identification of key parameters of virtual synchronous generator unified model under small frequency disturbance of power grid
ZHU Jun QU Yubo LIU Penghui GUO Xiangwei DU Shaotong
(Shool of Electrical Engineering and Automation, He’nan Polytechnic University, Jiaozuo, He’nan 454003)
Aiming at the diversification of virtual synchronous generator (VSG) control strategies of grid-connected inverters, a unified linearization model of virtual synchronous generators is established, and the identification method of the inverter’s actual output equivalent inertia and damping coefficient is proposed to quantify its support capability to the grid. From the perspective of grid frequency perturbation and considering the influence of phase-locked loop and filter in the inverter sampling link, a unified small-signal model capable of characterizing the dynamic and static regulation performance of the virtual synchronous generator is established. According to the established model, the zero-pole method is used to analyze the influence of control parameters on the system. The grid frequency disturbance and load disturbance are used to excite the system power dynamic information, and the stochastic gradient method based on the multiple new interest theory is used to identify the equivalent inertia and damping coefficient of the inverter output. Finally, the system simulation model is built to verify the correctness and effectiveness of the analysis and identification methods.
virtual synchronous generator (VSG); unified model; equivalent damping; equivalent inertia; parameter identification
2022-03-28
2022-04-18
朱 军(1984—),男,博士,副教授,研究方向为新能源发电技术、特种电机驱动与控制。
国家自然科学基金(U1504506)
河南省科技攻关项目(202102210093、212102210256)
河南省高等学校青年骨干教师培养计划项目(2020GGJS055)
