基于改进中值滤波的手机玻璃瑕疵图像增强方法*

巩玉奇 ，陶晋宜 ，杨 刚

（1.太原理工大学 电气与动力工程学院，山西 太原 030024；2.西安电子科技大学 超高速电路设计与电磁兼容教育部重点实验室，陕西 西安 710071）

0 引言

滤波去噪以及图像增强作为玻璃瑕疵缺陷分割以及瑕疵分类的前序步骤，其处理效果直接影响瑕疵的分割以及分类[1-2]。边缘检测主要是依据图像像素强度的变化来筛选出可能存在的边缘的像素点[3]，其数学模型实际上是通过计算像素点亮度的一阶导数或者二阶导数来确定。但是玻璃瑕疵的多样性造成的瑕疵图像的获取难度相当之高，不同的瑕疵需要不同的打光角度[4]，也需要不同的相机架设角度[5]，而同一张玻璃上面会同时存在不同的瑕疵，本文的玻璃瑕疵图像获取必须是具有一定的泛化能力的，基于瑕疵图像获取的不精确性，才更加凸显出图像处理的关键之处。

常用的滤波方法包括时域滤波和频域的滤波，目前主要有以下几种：均值滤波、方框滤波、双边滤波、高斯滤波以及中值滤波等。针对目前实验所拍摄的玻璃瑕疵图像的噪声，中值滤波能够比较有效地去除图像的噪点影响[6]，但是中值滤波对于图像的有用的边缘信息也会进行处理，这样就会影响处理后的图片清晰度，虽然噪声会有效去除，但是其清晰度的降低和边缘信息的损失会给后期的图像增强和分割造成困扰。因此，本文在玻璃瑕疵图像滤波去噪的环节采用一种带有条件判断的中值滤波方式，结合直方图均衡化，有效做到图像处理和增强效果[7]。

1 中值滤波原理

1.1 经典中值滤波

中值滤波器是顺序统计滤波器的一种，即用目标像素点邻域的灰度中值来代替该点的像素值，其数学形式表示如下：

其中，（s，t）∈Sxy，g（x，y）为中值滤波的输出值，f（s，t）为原始灰度值。Sxy表示中心在（x，y）、尺寸为m×n 的矩形子图像窗口的坐标组。传统的中值滤波思想是快速将像素集合进行排序来寻找中值，算法的执行速度由快速排序算法的时间复杂度决定[8-9]，其思路是，每次排序都将像素点集合划分为两个相互独立的子集合，其中一个子集合中所有像素值都比另一个子集合中所有像素值小，然后按照这个方法继续对上面所述的两个字集合进行排序，一直到选取的滤波窗口里面的所有元素做到按照数值排序，中值滤波的输出是该序列中的中位数。该方法从图片左上角到右下角逐个像素进行中值滤波，遍历所有像素点，得到最终的输出结果。

1.2 改进中值滤波

经典的中值滤波把目标缺陷及其边缘也无选择的进行滤波，这是该方法的缺陷，因此本文引进一种算法，考虑到缺陷边缘与背景的灰度差异且瑕疵灰度要大于背景灰度，本文设置一个判断条件：如果目标像素点的灰度值是处在该邻域内的极大值一定范围内的数值（该“一定范围”是考虑到瑕疵边缘灰度值相近，目标点像素值可能并不是极大值但是其仍然是瑕疵边缘的缘故而设置的。其数值大小需要根据瑕疵图像的灰度值进行设置，这里用k 表示其波动范围），那这个像素点就很有可能是本文感兴趣的缺陷的边缘，则该点就不进行滤波处理，反之则进行滤波处理。该部分具体算法流程如图1所示，该算法就会很大程度降低图像滤波所带来的信息的损失。其中，p为目标像素点（x，y）处的灰度值，k 为设置的波动范围，max 为（x，y）点邻域内的极大值。

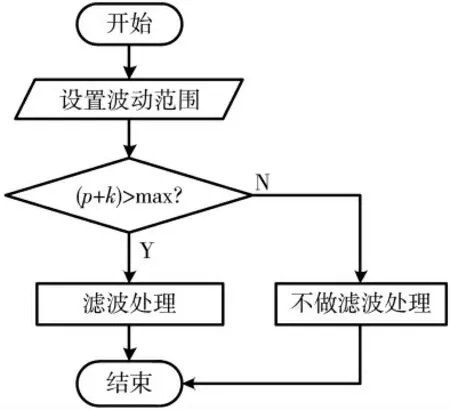
图1 改进中值滤波判断流程

2 直方图均衡化

图像的空间域处理是两大图像处理技术之一，图像空间域处理是对图像的像素进行处理的，空域滤波和灰度变换是常用的两种手段。直方图均衡化（Histogram Equalization）就是一种常用的灰度变换方法[10]。对于灰度级范围属于[0，L-1]的数字图像，其直方图可以表示如下：

其中，rk是第k 级灰度值，nk是图像中灰度值为rk的像素个数，即图像的灰度直方图表征的是高图像的灰度分布。一张面阵相机拍摄下的玻璃瑕疵图片的直方图如图2 所示。

图2 玻璃瑕疵直方图

其中横轴为灰度值，纵轴为次数histogram 为灰度值出现的次数，cdf 为该灰度值从小到大累计出现次数。在实际应用当中，通常先对直方图归一化，然后再做后续的处理，如果灰度图像的维数是M×N，归一化直方图可以表示为：

即p（rk）表示灰度级rk在图像中出现的概率的估计，归一化直方图所有分量之和等于1。直方图均衡化的基本思想是让输入图像的直方图分布变得更加均匀，这样就会使图像的灰度级增加，可以让图像的对比度整体增强。假设未处理前的图像在二维坐标系当中，令其灰度值在（x，y）处为f（s，t），处理后其灰度值为g（x，y），g（x，y）则可认为当f 转变为g 时，就实现了对图像效果的增强。综上，可将其转换函数表示为：g=EQ（f），这个映射函数EQ（f）必须满足两个条件（其中L 为图像的灰度级数）：

（1）为使输入图像的灰度排列不被打乱,在区间0≤f≤L-1 内，EQ（f）必为单调递增函数。

（2）为使转换前后灰度不发生动态变化，当0≤f≤L-1时，必有0≤g≤L-1。

3 实验及分析

3.1 实验方法

为了保证本实验的方法对手机盖板玻璃瑕疵图像处理的泛化性以及提升本算法的鲁棒性，本实验使用50 张现实中厂家生产淘汰的手机玻璃瑕疵盖板，其实验素材来自于蓝思手机玻璃盖板制造商，瑕疵包括划痕、坑点、崩边、墨点、压痕等不同种类的玻璃瑕[11-12]。由于实验室部分仪器的缺乏，因此采取面阵相机获取图像[13]，打光方式采用黑暗背景下LED 条形光源对称打光，反射的结构光被相机捕捉，瑕疵可见[11]，获得的图片分辨率为638×1350。

3.2 实验内容及结果

本实验主要用到的软件是Anaconda 以及MATLAB，通过Python 语言来实现算法的程序编写。首先对一张含有玻璃瑕疵的图片进行拍摄，获取其图像图像，用传统的中值滤波进行滤波处理，然后再用直方图均衡化对其进行增强处理，随后用MATLAB 三维显示其灰度值，如图3 所示。

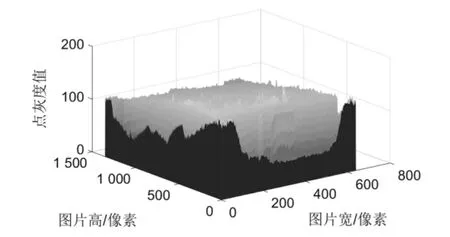
图3 原始玻璃瑕疵图像灰度值三维显示

经典方法处理后的图片用MATLAB 三维显示其灰度值效果，如图4 所示。

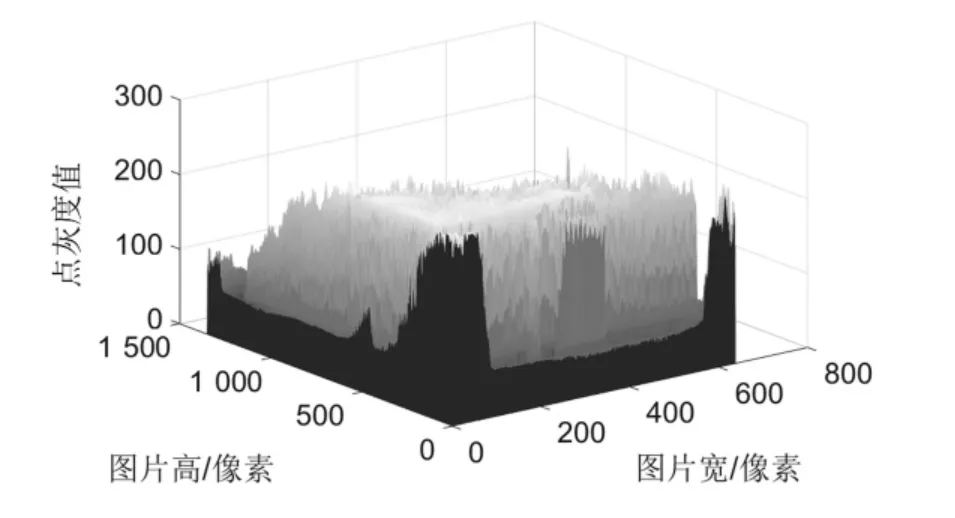
图4 经典方法处理后的灰度值三维显示

不难看出缺陷的可见度确实进行了增强，但是也发现图像整体灰度值偏亮[14]，这是由于本文实验所用的玻璃瑕疵都是有代表性的，一张图片上存在各种各样的瑕疵，且每种瑕疵的数量不止一个，这就造成了直方图处理后的整体效果变亮。有一种采用有限对比度动态四直方图均衡化方法在保持亮度和结构的情况下进行图像增强[15]，但是实验室下此方法对于本文玻璃瑕疵图像不适用。即便如此，经典的算法处理还是有效果的，只是其边缘信息会损失，与背景的对比度没有特别理想罢了。

下面用本文所述改进的算法对同一张图片进行处理，其灰度值三维显示如图5 所示。

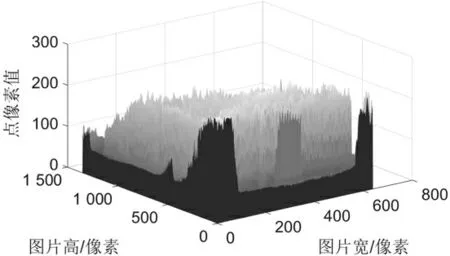
图5 本文方法处理后的图像灰度值三维显示

对比观察图4 和图5 可以发现，尖峰位置也就是图片有用信息的突显度更加明显，也就意味着瑕疵更加清楚，这正是因为本文方法对非瑕疵边缘信息的选择性滤波所起到的作用。虽然从图像的直观表达可以看到其效果的好坏，但是对带有噪声的图像进行去噪和增强处理之后的图片质量的评估，往往需要数据作为指标去支撑和衡量。下面从数据角度对本文的方法所处理的图片进行评估。本文首先引入峰值信噪比 （Peak-Signal-To-Noise Ratio，PSNR）来对图像质量进行评估。首先要知道信噪比（Signal-To-Noise Ratio，SNR），即信号和噪声的比值：

其中，μsig表示信号，σbg表示噪声。针对一张图像，信号值就是灰度值。分母有时候采用背景信号值得方差，其代表的物理意义是噪声的功率。然而对于高对比度黑色背景图，上式直接计算会是无穷大，因此本文改用信号均值与信号的标准差来衡量：

其中，σsig表示信号的标准差。这是信噪比的定义，然而对于图像评估而言，通常不知道感兴趣的像素点与噪点的区别，因此信噪比往往没办法直接得到，一味地用信噪比来衡量会让实验难度增加，往往效果也不尽人意，因此本文用峰值信噪比来评估图像处理结果质量。PSNR 是图像处理领域一个非常重要的测量指标，其简单地通过均方差（Mean Squared Error，MSE）来定义。两个m×n 的图像I 和K，均方差定义为：

峰值信噪比定义为：

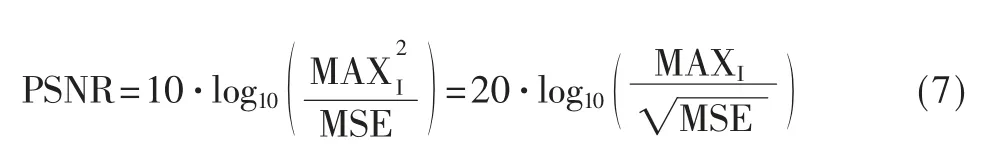
其中，MAXI表示图像点颜色的最大数值，本文中所有灰度图像的灰度范围均为0～255，因此MAXI=255。PSNR作为目前图像处理领域应用最为广泛的数值评估方式之一[16]，虽然很方便，但也有其相当明显的局限性，其局限性在于不够接近人眼的直观感觉。从其计算公式可以看到，它的评价指标是基于逐个像素点的，即一幅图像中的每个像素点对图像的质量结果输出的权重是相同的。这从人眼的角度看是非常不合理的，但是其局限性在本文玻璃瑕疵检测领域里面刚好被无限地弱化，因为玻璃瑕疵检测本身就是机器视觉领域的研究，对人眼观察时感受的不合理性对本文研究的影响本文不予考虑。PSNR 是基于MSE 定义的，两者的计算出发点都是遍历每个像素点的灰度值，是两张图对应像素的比较。除此之外本文还用另外一个指标——结构相似性（Structural Similarity Index Measurement，SSIM）来评价图像质量，其不仅考虑到对应像素的数值对比，还从图像的结构上对图像处理后整体的质量进行评估，其结果也会反映出本实验方法对于玻璃瑕疵边缘信息的保留程度。SSIM 公式基于样本x 和y 之间的3 个比较衡量：亮度（luminance）、对比度（contrast）和结构（structure）：

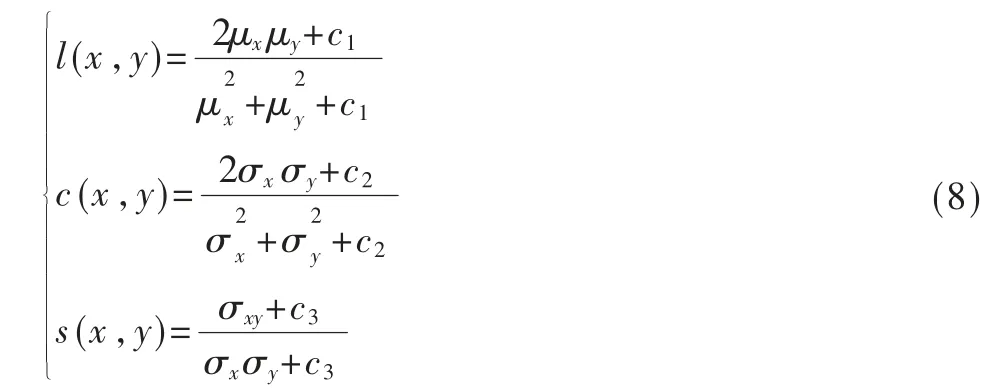
其中，μx为x 的均值，μy为y 的均值，为x的方差，为y 的方差；σxy为x 和y的协方差；c1=（k1×L）2、c2=（k2×L）2为两个常数，避免除零，L 为像素值的范围，数值为255，k1=0.01，k2=0.03 为默认值，一般取c3=c2/2。那么：

将α，β，γ设为1，可以得到：

每次计算的时候都从图片上取一个正方形窗口，然后不断滑动窗口进行计算，最后取平均值作为全局的SSIM[17]。

将经典方法得到的图像（图4）和本文方法所得到的处理后的图像（图5）分别与原始图像（图3）对比，求出这3 个评估数据，结果如表1 所示。

表1 单张玻璃3 项实验数据对比

从玻璃盖板生产厂商采购50 张带瑕疵的样本，其瑕疵种类齐全且数量足够。下面对这50 张图片按照本文所述思路依次进行处理，并对其图像质量的3 个评估数据进行记录并取平均值，从而得到表2。

表2 50 张图片3 项实验数据平均值对比

3.3 实验结果分析与结论

分析以上实验结果，从三维灰度显示的直观感受角度看，改进中值滤波后其瑕疵边缘信息损失极少，图片增强后对比度的提升也使瑕疵更加清楚；从数据定量的角度来看，3 项数据都有提升：MSE 提升了64.6%，PSNR提升了16.4%，SSIM 提升了7.6%。一般认为PSNR 在20 dB～30 dB 区间时，其图片质量较好，在30 dB～40 dB区间时，其图片质量很好。本文方法相对于经典方法，图片的PSNR 从27.44 dB 提升到31.95 dB，其效果还是比较理想的。SSIM 看似提升的幅度不高，但是这主要是因为其值最大为1，越接近1 效果越好，这造成了SSIM 在高水平下提升难度很大，结构相似度的提升正是因为玻璃瑕疵边缘信息保留完整的结果，0.947 的结构相似度也达到预期。综合以上结果，不论是从灰度三维显示的直观感受来看，还是从3 项评估指标来看，本方法效果有效。

4 结论

本文介绍了一种基于改进中值滤波的玻璃瑕疵图像增强方法，通过实验对比发现，本文改进的玻璃瑕疵图像增强办法相较于传统方法，玻璃瑕疵感官上的可见性以及处理后玻璃图像的质量都有所提升，3 项数据的提升幅度各有不同，但是作为图像重要评估标准的PSNR越过30 dB 的分界线，其质量的提高是显而易见的。从SSIM 数据来看，增强后的图像和原图在结构上相似度非常高，这意味着对玻璃瑕疵信息增强的同时并没有破坏其应有的瑕疵边缘。综上所述，本文方法对玻璃瑕疵图像边缘信息保留的同时也起到了滤波和增强效果，其结果也为接下来玻璃瑕疵图像的分割以及瑕疵分类奠定了坚实的基础。