基于模糊PID的振捣机器人重心控制系统研究
2022-07-21司癸卯
司癸卯,曾 强,乔 桐
(长安大学道路施工技术与装备教育部重点实验室,陕西西安 710064)
混凝土作为土木工程中广泛运用的材料,其在浇筑时必须振捣充填模板、钢筋与预埋件之间的间隙,同时排出裹挟在拌合物中的气泡从而达到密实成型效果[1-2]。目前,我国混凝土施工作业大多是由人工完成的,在实际振捣作业中,操作人员无法像机器一样稳定地对混凝土进行振捣作业,常使作业质量达不到要求。为了提高振捣混凝土构件质量,在很多规模大、质量要求高的施工作业中,往往会使用振捣机器人来进行振捣作业,以提高振捣效率和精度。
振捣机器人在进行振捣作业时,由于振捣棒及伸缩杆在作业过程中会根据实时作业情况不断地调整位置,将导致振捣机器人的重心产生变化。振捣机器人在重心变化时,往往会产生振动、倾斜、侧翻等不良情况,因重心变化而产生的振捣机器人位姿变化会极大地影响振捣质量,甚至会出现安全事故。因此,为了提高振捣质量,确保施工安全,对振捣机器人的重心进行实时控制是有必要的。控制振捣机器人重心的主要执行元件为液压机构,其响应时间相对较长,且控制精度较差[3],同时考虑到振捣机器人在作业过程中的复杂工况,传统的PID控制策略难以达到良好的控制精度要求。现采用一种基于模糊PID 的控制方法,通过对液压缸的伸缩量进行控制来实现配重块的实时运动。
1 重心控制系统模型
1.1 振捣机器人的结构原理
振捣机器人的结构如图1 所示,其主要由振捣装置、配重装置、机械臂以及底盘组成。在振捣作业时,振捣装置在机械臂的作用下到达指定工作位置,机械臂可以实现振捣装置在3 m 范围内的自由运动,在振捣装置到达指定工作位置时振捣器开始工作[4]。此时因为机械臂的伸缩,振捣机器人的重心开始变化,故为了控制其重心,防止振捣机器人发生倾覆,需要通过液压缸来实时调节配重装置的位置,以实现对振捣机器人重心的实时控制。考虑到重心控制过程中需要对配重块的移动速度、实时位置进行精确的控制,故而需要对液压系统进行理论分析和控制仿真,以实现对振捣机器人重心的准确控制。

图1 振捣机器人结构模型Fig.1 Structural model of vibrating robot
1.2 电液控制系统设计
根据实际工况分析,为保证施工质量和安全性,在振捣机器人作业过程中需要保证配重块与振捣装置随动。振捣机器人的配重装置由配重块和液压系统组成,配重块由一个移动油缸进行控制。当振捣机器人开始工作时,位置传感器检测机械臂的运动,并将运动信号发送给上位机,上位机中的软件对位置信号进行分析计算,得出配重装置所需要移动的距离,同时将信号传给控制器。控制器根据位移的距离控制方向阀的动作,在方向阀的作用下,液压系统中液压缸开始工作,推动配重装置与振捣装置随动,从而实现对振捣机器人重心的实时控制[5]。如图2 所示,T 为回油路,来自进油路P 的油液进入换向阀,通过对其接入工作位的控制而改变进入移动油缸的油液方向,从而控制配重块的移动方向。回路中的液压锁可以锁死液压回路,防止液压缸在配重装置的带动下滑动;溢流阀在液压回路中做安全阀用,防止液压回路中油液压力过高而产生安全事故。

图2 重心控制系统液压原理Fig.2 Hydraulic schematic diagram of gravity center control system
1.3 液压控制系统的数学模型
通过换向阀来控制移动油缸的移动,建立该液压系统液压缸和换向阀的线性化流量方程以及力平衡方程。
换向阀的线性化流量方程为
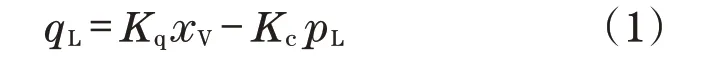
液压缸的线性化方程为

负载力平衡方程为

式中:xV为换向阀的阀芯位移;PL为阀的负载压力;qL为负载流量;Ff为配重块摩擦力;Kq为阀的流量增益;Kc为流量-压力系数;Ap为液压缸工作面积;Ctp为液压缸总泄漏系数;Vt为液压缸(含油管)总压缩容积;βe为封闭在阀和缸之间的油液等效体积弹性模量;Bp为配重块阻尼器阻尼;m为配重块质量;xV为换向阀阀芯位移;xL为配重块位移;Fk为外负载力。
各参数取值如表1所示。

表1 相关参数取值Tab.1 Value of relevant parameters
将上述数据带入传递函数中得

2 模糊PID控制系统
2.1 模糊PID自动控制策略
该控制系统使用PLC控制比例方向阀,并通过方向阀控制油缸,为了实现闭环控制,油缸选用带位置测量的单杆液压缸。在电液控制系统控制配重装置运动时,液压缸向PLC传输位置信号,PLC在接受信号后再将控制信号传给方向阀从而控制液压缸运动,此时液压缸的位置测量装置再次向PIC传输位置信号,实现控制系统的闭环,其原理如图3所示。

图3 控制系统流程Fig.3 Control system flow chart
考虑到振捣机器人在工作时,其配重装置的移动速度较慢、质量大,并且工作环境较为复杂,传感器的检测不一定精确。若采用普通的PID控制,很难排除现场复杂工况对控制系统的影响,故采用适应性和鲁棒性较好的模糊PID控制。模糊控制在实际应用中,可以减小因位移传感器测量误差而导致的重心控制系统失稳的状况,并且也可以尽量地减小现场光污染、噪声对控制系统的影响。其控制原理如图3所示。模糊自适应PID控制器中的输入e、ec分别表示移动油缸活塞杆的位移偏差和偏差的变化率,也就是配重装置被液压缸推动时的位移偏差及偏差变化率,通过模糊化和模糊推理将ΔKp、ΔKi、ΔKd作为模糊输出变量,在重心控制的过程中通过实时的检测位移偏差值对PID参数进行修正,从而实现对重心的控制。

图4 模糊PID控制原理Fig.4 Block diagram of fuzzy PID control principle
2.2 模糊规则与函数
在模糊控制器中主要执行模糊化、模糊推理和参数清晰化的运算,将e、ec作为输入,并对这2个变量模糊化,将其分成8个部分,根据变量输入值的大小,判断其在各个隶属度的百分比大小,确定其隶属度。
其中输入输出都设置为7个隶属度函数{NB,NM,NS,ZO,PS,PM,PB},其分别表示{负大,负中,负小,零,正小,正中,正大}[6]。根据实际工作情况确定e、ec的模糊论域为{-3,-2,-1,0,1,2,3}。ΔKp、ΔKi、ΔKd的变化范围:ΔKp为[-2,2],ΔKi为[-8,8],ΔKd为[-0.05,0.05]。其具体隶属度函数如图5所示。

图5 隶属度曲线Fig.5 Membership curve
在输入到输出之间的模糊化是需要确定具体的模糊规则,模糊规则的制定需要综合考虑到系统的稳定性、响应速度和超调量以及这三者之间的关系[7]。模糊规则的制定一般要根据2个输入的参数大小来确定比例系数、积分系数以及微分系数的大小。在PID 控制器的3 个输入量中,ΔKp、ΔKi、ΔKd分别决定着系统的响应速度、稳态偏差和动态特性。在控制过程中,应根据实际工作过程调节此3个参数。例如在液压缸运动初期,为了能够尽快地稳定重心,一般要求取较大的Kp值,但是为了防止在控制过程中产生较大的超调,在中期通常要减小Kp值,在控制末期要再次将Kp值调到较大值来减小静差;在系统中可以通过调节Kp值的大小来减小稳态偏差,在控制过程中系统往往会在初期产生超调,此时需要改变Kp值弱化积分的作用,在液压缸运动的中期,往往需要增大积分的作用以增加系统的稳定性;微分环节是考虑到系统的惯性过程而引入的参数,在液压缸运动过程中可能会出现移动距离偏差过大的情况,而微分系数则能够反映信号的变化趋势,及时地修正液压缸的运动[8]。
通过调节比例系数、积分系数和微分系数的大小可以实现对系统的响应速度、稳态误差以及动态特性的最优控制。该3个系数通过相互调节可以使系统获得良好的特性。其具体的模糊规则见表2。

表2 模糊规则表Tab.2 Fuzzy rule table
3 Matlab仿真
3.1 仿真模型设计
根据振捣机器人液压系统的模型和其传递函数,通过Simulink 对其液压缸的运动进行仿真[9]。为了更好地比较模糊PID 的控制特性,在仿真器内加入经典PID 控制,比较两者在稳定性、超调量和响应时间上的优劣[9]。Simulink 仿真模型如图6所示。仿真模型中输入信号为阶跃信号,通过Simulink 内置的PID 和fuzzy PID 控制模块对信号进行仿真。

图6 仿真模型Fig.6 Simulation model diagram
3.2 仿真结果分析
图7 为Simulink 仿真结果。模糊PID 控制下液压缸在1.47 s 时第一次到达指定位置,并在2.32 s 时进入稳定状态,虽然在到达稳定状态前有一个较小的波动,但是波动很快地被抑制了下去并进入稳态,而经典PID 在2.14 s 时到达指定位置并在6.73 s 时才进入稳定状态,同时模糊PID 的超调量也比经典PID 减少了0.02 m。可以得出模糊PID 在响应时间、超调量和稳定时间上都比经典PID优越。
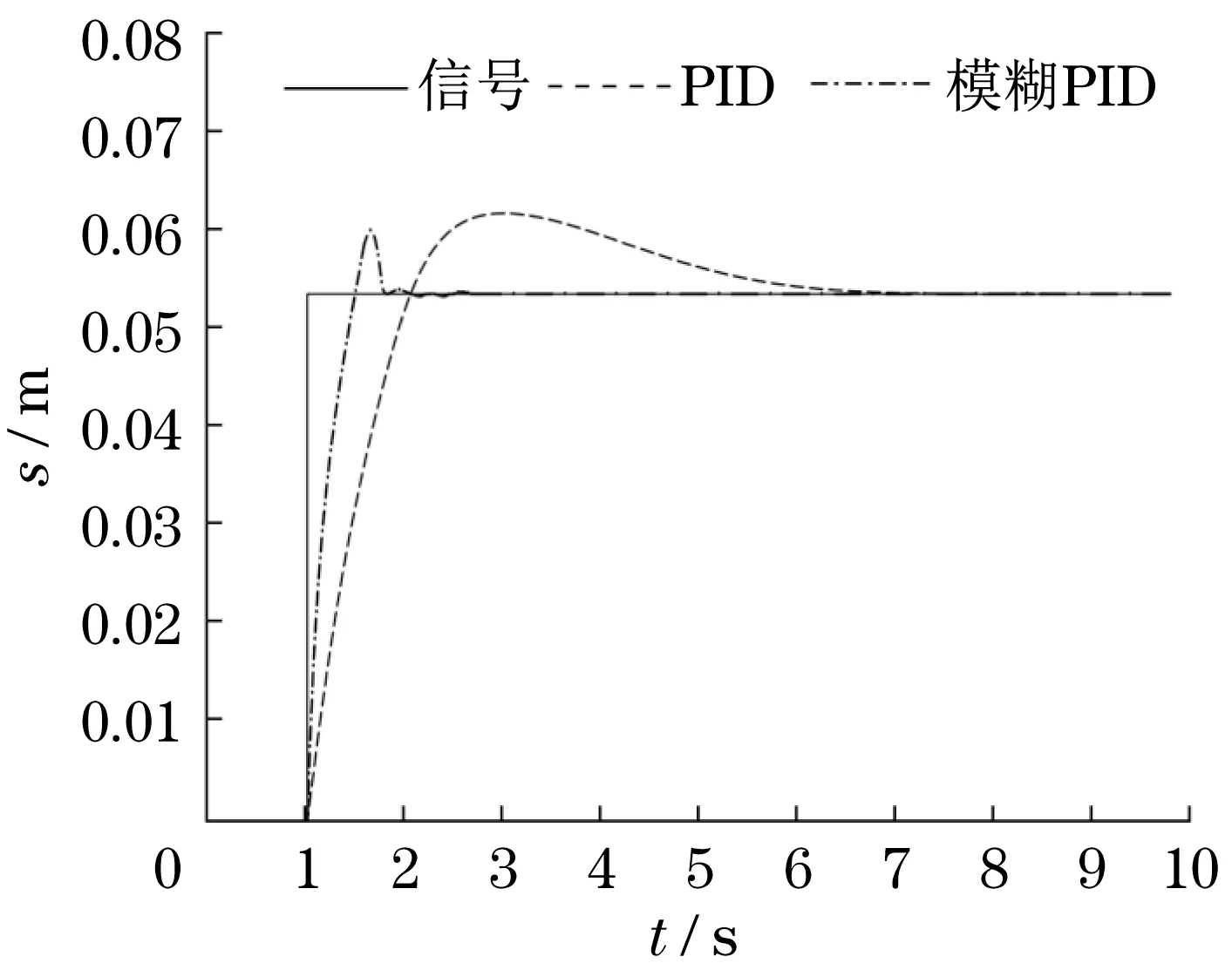
图7 Simulink仿真结果Fig.7 Simulink simulation results
4 结语
本文根据振捣机器人实际工作情况,设计了重心电液控制系统,并引入了模糊PID 控制策略,在Simulink 中构建了电液控制系统的仿真模型,通过对相关参数的调节使仿真结果达到了预期的效果,证明了所设计的电液控制系统可行、控制策略可靠,为振捣机器人的研制提供了理论依据。
