RP型刚柔机械臂螺栓结合部等效建模及结构特性分析

张文辉，闻 志，游张平，沈金淼，3，叶晓平

（1.南京晓庄学院电子工程学院，江苏南京 211167；2.浙江理工大学机械与自动控制学院，浙江杭州 310000；3.丽水学院工学院，浙江丽水 323000；4.浙江省航空航天金属导管塑性成形技术与装备重点实验室，浙江丽水 323000；5.浙江省文创产品数字化设计与智能制造重点实验室，浙江丽水 323000）

柔性操作臂相比刚性操作臂具有轻质、高速、能耗低等优点，近年来越来越受到产业界和学术界的关注［1-2］。目前，以Rotation-Parallel（RP）型为代表的刚柔机械臂正逐渐应用于医疗器械领域。该机械臂主要由一个旋转刚性臂通过移动基座连接一个末端柔性臂，具有较大的工作空间，能够实现平面内大范围快速移动和精确定位，因此对其进行深入研究具有重要意义［3］。但由于RP 型刚柔操作臂在运动过程中存在着大范围的刚体运动与小位移的弹性振动［4-5］，这种弹性振动会通过螺栓结合部影响机器人刚性臂杆的动态特性，并导致末端执行器的定位精度变差和工作效率的降低［6］。螺栓结合部是由多种复杂结合面之间相互耦合组成，从而使得螺栓结合部表现出一种不相容性、非线性等特性［7］，作为构件之间固定连接的主要形式之一，表现出的复杂动态特性对整个机械系统的结构特性产生较大的影响［8］。

螺栓联接因其具有可靠性强、拆卸方便等优点被广泛应用于结合部联接［9］。在整个机械系统中60%～80%的结构刚度和大约90%以上的结构阻尼均来自于结合部［10］，成为整个机械系统误差的主要来源，但由于其复杂的结构特性，无法采用传统的有限元方法对其直接进行建模和分析。因此，研究一种能够精确反映结合部特性的建模方法具有重要意义。

由于结合部相互接触的结合面构成一个封闭结构体，而结合面之间是由无数非连续接触的微凸体构成的，因此国内外学者试图从微观产生机理方面去揭示螺栓结合部的结构特性［11］。1966 年，Greenwood 等［12］根据粗糙表面之间的接触形态，率先提出GW 模型，为此类问题的解决开辟了新思路。Li 等［13］建立了粗糙表面与刚性平面之间的塑性变形模型。尤晋闽等［14］进一步考虑了微凸体在弹性、弹塑性以及完全塑性变形之间相互连续转化，提出了适用于粗糙接触表征的统计模型。Yoshimura 等［15］提出等效结合部的弹簧阻尼单元模型。李院生等［16］根据刚度等效原则，建立了单螺栓结合部的弹簧阻尼单元模型，并实验验证了模型的合理性。Hui 等［17］基于虚拟材料层法对螺栓结合部进行等效建模，并且通过基础特性参数计算出虚拟材料的弹性模量及泊松比。张学良等［18］用一层各向同性虚拟材料作为结合部的等效模型，研究结合部在法向、切向上的不同特性。Williams 等［19］利用弹簧单元模型，分析外载荷作用下结合部的变形与螺栓预紧力大小之间的关系。

综上，研究螺栓结合部受力状态，确立结合面接触面压与螺栓预紧力的关系表达式，建立螺栓结合部等效模型，推导螺栓结合部切向刚度方程和法向刚度方程，探究螺栓预紧力、螺栓直径、数目以及排列方式等对结合部动态特性的影响规律具有重要意义。

1 螺栓结合部等效建模

1.1 螺栓结合部受力分析

螺栓结合部在工作中受到预紧力F以及预紧力矩T的作用，具体如图1所示［20-21］。

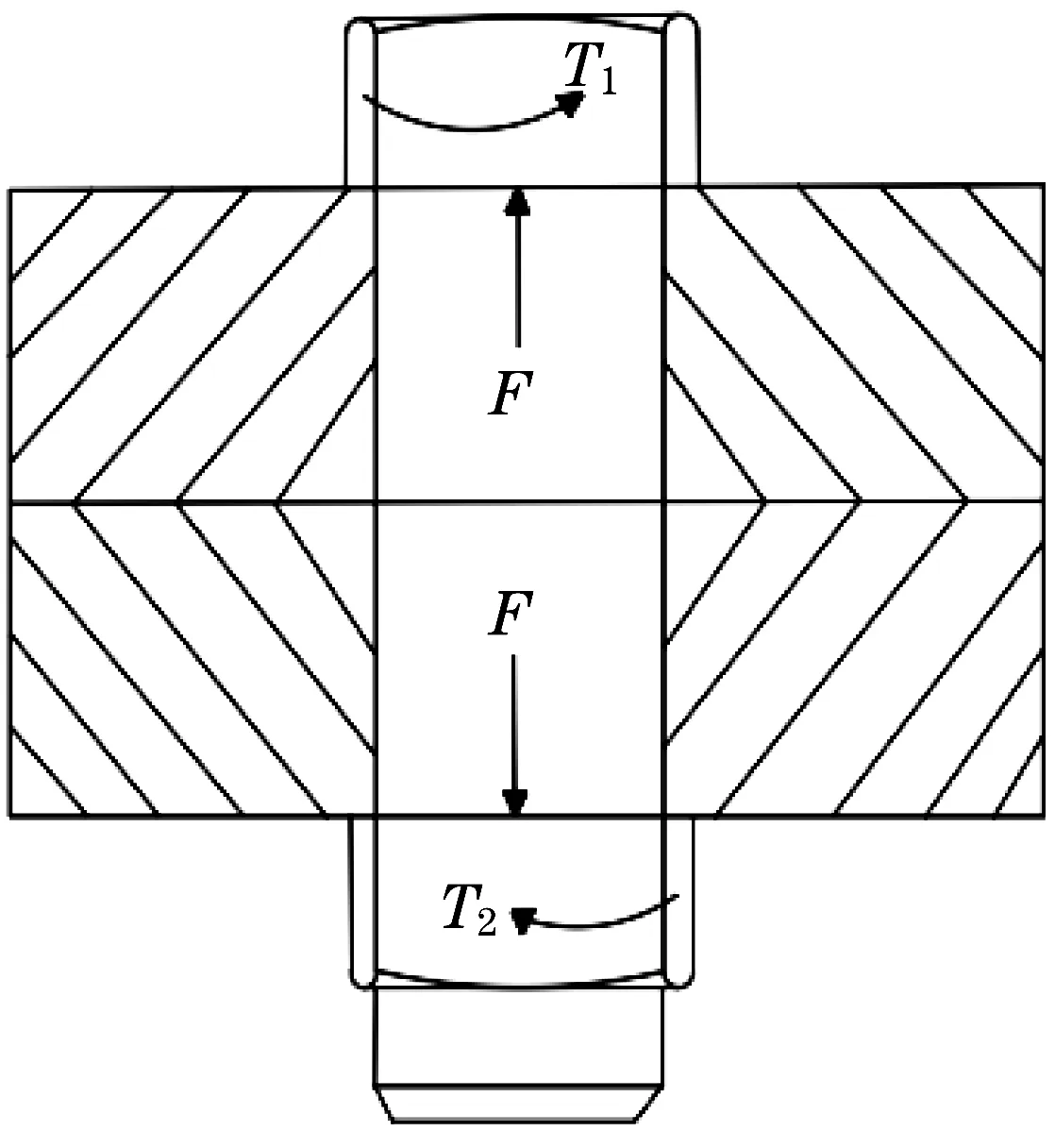
图1 螺栓结构受力Fig.1 Stress diagram of bolt structure

螺栓预紧力矩T由螺母与构件表面之间的摩擦力矩T1、螺旋副之间的摩擦阻力矩T2组成：

式中：μ为螺母摩擦系数；F为螺栓预紧力；r为螺母当量摩擦半径；D为螺母外径；d0为螺栓孔直径；d1为螺纹中径（d1=0.9d，d为螺纹的公称直径）；θ为螺纹升角；α为螺旋副的当量摩擦角。

将式（1）～式（4）联立，可得螺栓预紧力与预紧力矩之间的关系为

结合面接触面压Pn与螺栓预紧力F的关系可表示为

式中：S为结合面面积。

1.2 螺栓结合部等效建模

基于有限元法得到螺栓结合部的应力分布云图如图2 所示。当连接构件的螺栓受到预紧力作用时，在螺栓孔周围的一定区域内分布着不均匀的接触面压，并随着远离中心而越来越小，说明螺栓结合部的接触面压力影响具有局部性。

图2 螺栓结合部的应力分布云图Fig.2 Stress distribution nephogram of bolt joint

考虑到螺栓影响区域的区域局部性，给出螺栓影响区域的模型如图3所示。

图3 螺栓影响区域模型Fig.3 Bolt influence area model

图3 中，上、下构件通过一个直径为d0，螺栓头部直径为Dw的螺栓固定连接。从图中可以看出，螺栓的接触面压影响区域Dc整体上呈现截头圆锥体分布，进而影响着区域内的压应力呈现非线性分布。

根据Yoshimura 等［15］提出的弹簧等效理论，设计螺栓结合部等效模型如图4所示。

图4 中螺栓孔的周围均匀分布4 组弹簧单元，每组弹簧单元包括1 个法向单元和2 个切向单元。对每个弹簧单元采用由弹簧-阻尼器组成单元模块进行等效，如图5所示。

图4 弹簧单元模型Fig.4 Spring element model

图5 弹簧-阻尼器等效单元结构Fig.5 Spring damper equivalent element structure

2 螺栓结合部刚度特性函数方程

2.1 结合部法向刚度方程

为方便分析结合部法向载荷与法向刚度之间的关系，进行如下假设：①结合面之间为刚性光滑表面与粗糙表面之间的接触；②法向载荷对结合面上各部分载荷均相同。

单个弹性微凸体与一个刚性平面之间发生接触变形的模型如图6所示。

图6 微凸体法向变形模型Fig.6 Normal deformation model of micro convex body

将粗糙表面等效为多个微凸体，令单个微凸体的等效曲率半径为r，顶部的变形量为ξ，接触半径为a，法向载荷为Fn，根据赫兹接触理论可知，单个微凸体法向载荷Fn与顶部变形量ξ之间的关系为

式中：E为微凸体之间的等效弹性模量，且E=，其中E1、E2为两粗糙表面的弹性模量，μ1、μ2为两粗糙表面的泊松比。

根据法向刚度定义，对式（6）中的顶部变形量ξ求导，可得单个微凸体的法向刚度为

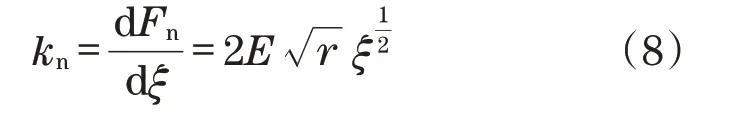
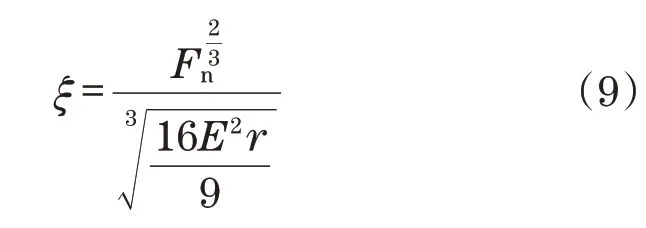
将式（9）带入式（8）整理可得微凸体法向刚度与法向载荷之间的关系为

将式（10）经过赫兹理论变换可得到法向刚度kn与接触面压pn之间的关系为

式中：αn、βn为单位面积上结合面的法向基础特性系数。

2.2 结合部切向刚度方程

在实际工况中，结合部不仅受到法向载荷Fn作用，同时也会受到切向载荷Fτ作用。当接触微凸体受到切向载荷作用时，微凸体会发生切向变形，具体如图7所示。

图7 微凸体切向变形模型Fig.7 Tangential deformation model of micro convex body

结合面切向变形量：

式中：μ为静态摩擦系数；K为粗糙表面等效切向模量；K1、K2为两粗糙表面切向模量；μ1、μ2为两粗糙表面的泊松比。

根据切向刚度定义，两微凸体接触时切向刚度为

将式（15）经过赫兹理论变换，可得切向刚度kτ与接触面压pn之间的关系表达式为

由于微凸体面积远小于接触面面积，将单个微凸体切向刚度kτ等效为单位面积上接触体切向刚度，可得切向刚度kτ与接触面压pn之间关系的函数方程为

式中：ατ、βτ为单位面积上结合面的切向基础特性系数。

则结合面总的法向刚度Kn和切向刚度Kτ为

式中：S为结合面的接触面积，m2。

3 基于ANSYS螺栓结合部结构特性分析

选用螺栓结合面材料参数如下［8］：45#钢，表面粗糙度为0.8 μm。滑座和柔性臂通过螺栓连接，其中柔性臂薄板尺寸为300 mm×100 mm×6 mm，刚性滑块基座尺寸为150 mm×150 mm×100 mm。单位面积上结合面的基础特性系数分别为αn=3.26，βn=0.60，ατ=0.27，βτ=0.48。

3.1 螺栓结合部力学特性分析

3.1.1 不同预紧力下螺栓结合部力学特性

对螺栓分别施加20、30、40、50 N·m 的载荷，并根据所建立的弹簧单元模型进行自由模态分析。

联立式（4）、式（5）带入式（12）和式（17），可得到不同预紧力矩下结合面的法向刚度和切向刚度值，具体见表1。

表1 不同预紧力矩下结合部刚度Tab.1 Joint stiffness under different pre tightening torques

利用有限元分析方法，基于ANSYS 得到不同预紧力下结合面压力云图如图8所示。

由图8 可知，螺栓结合部接触表面在不同的预紧力矩下，越靠近孔边缘的地方接触压力越大，远离孔边缘的接触压力逐渐减小。且当螺栓预紧力矩从20 N·m逐渐增大到50 N·m时，其接触压力最大值从971.12 MPa 增加到1 087.4 MPa，说明增大预紧力矩会增强接触面的压力强度。

图8 不同预紧力矩的压力云图Fig.8 Pressure nephogram of different pre tightening torques

3.1.2 不同型号螺栓结合部力学特性

选取常用的M6、M8、M10、M12 几种型号的螺栓，研究螺栓型号对结合面接触面压的影响规律。设定螺栓的预紧力矩40 N·m。利用ANSYS 有限元法得到接触表面的压力分布云图如图9所示。

图9 不同螺栓型号接触表面压力云图Fig.9 Pressure nephogram of contact surface of different bolt models

由图9 可知，在预紧力矩相同的情况下，当螺栓直径从M6 增加到M12 的过程中，其最大压力值分别为980.51、721.02、455.37、377.88 MPa，说明增大螺栓直径会减弱接触面的压力强度。

3.2 螺栓结合部模态频率特性分析

不同的螺栓数量对结合面的接触压力强度也不同，需要探究螺栓数量对结合部动态特性的影响机理。

基于Pro/E 建立不同螺栓数量下结合部模型如图8 所示，为保证结合面接触面压相同，设定每种方式总的预紧力矩均为40 N·m。

联立式（4）～式（17）解算，可得结合面的法向刚度为kn=2.38×1010N/m，切向刚度为kτ=1.59×109N/m。将PRO/E 模型导入ANSYS 进行联合仿真，可得前6阶固有频率，如图11所示。

图11 螺栓数量与固有频率关系Fig.11 Relationship between bolt quantity and natural frequency

由图11 可知，螺栓预紧力矩相同的情况下，随着螺栓连接数目的增加，结合部固有频率逐渐增大。因为在相同的螺栓预紧力矩作用下，结合部之间相互接触的微凸体数目逐渐增多，结构抵抗变形的能力增强，结合部刚度也随之增大，其固有频率也相应增大。因此，综合考虑图10（d）的排列方式更优。

图10 单一排列的不同数量螺栓模型Fig.10 Different number of bolt models with single arrangement

4 结语

螺栓结合部是刚柔机械臂的关键连接部件，本文基于等效模型分析其结构特性，研究了螺栓结合部受力状态，确立了结合面接触面压与螺栓预紧力的关系表达式，基于弹簧等效原理，建立了螺栓结合部等效模型；基于微凸体变形模型和赫兹接触理论，分别推导了螺栓结合部切向刚度方程和法向刚度方程；通过PRO/E 建立了螺栓结合部三维模型，采用ANSYS 进行了联合仿真，分析了螺栓预紧力和直径对结合部力学特性的影响规律和螺栓数目对结合部模态频率特性影响机理。