量子导引在量子通讯中的作用
2022-07-20杨挪亚
杨挪亚,李 崇
(大连理工大学物理学院,辽宁大连 116024)
0 引 言
1935 年,Einstein 等[1]提出EPR(Einstein-Podol‐sky-Rosen)佯谬,随后,Schrödinger 团队[2-3]提出量子纠缠的概念,从而揭示了量子理论的非局域特性,促使人们从理论和实验的角度来研究这种新的特性.量子非局域特性涉及量子关联[4]、量子纠缠[1-3]、量子导引[2-3,5]和Bell 非局域性[6]等一系列概念.同时,学者们也在研究如何利用量子非局域性进行高效、安全的计算、通讯和计量等,随之而来诞生了量子信息学[7]和量子计量学[8].
经过近30 年突飞猛进的发展,量子信息技术在理论和实验方面已经取得了显著的成果[9].量子非局域性在量子信息过程中的应用也取得了一定的进展,但是量子导引在量子通讯过程中的作用仍没有被研究清楚[10].量子导引作为量子非局域关联中重要的一种形式,具有非对称性、单配性等独特的性质,其中非对称性指量子导引双方的地位不相同,而单配性指量子导引在多体间不能自由分享.这些独特的性质在通讯过程中会满足若干特殊条件的通讯要求.因此,研究量子导引在量子通讯过程中的作用十分必要,量子导引也被视为多种量子信息过程中的一种有用资源.在与单边设备无关的量子密钥分发过程中,利用量子导引可以提高获取密钥的速率[11];在子通道识别任务中,使用任意导引态都优于非导引态,导引态能将任务完成得更好[12];在双方地位不对等的通讯过程中,必须利用量子导引的单向性才能使整个通讯过程安全、有效地完成[10].研究量子导引在量子隐形传态、远距离量子态制备和密集编码等已有量子通讯过程中的作用,提高协议的效率、安全性以及具体效果具有十分重要的意义.
本文主要研究通道量子导引在远程量子态制备和量子隐形传态这2 种量子通讯过程中发挥的作用.首先利用基于熵不等式的量子导引度量方式对选择的通道量子态进行度量,然后计算2 种过程中所使用通道量子态的保真度,再将得到的物理量进行比较,最终得到通道量子导引对量子通讯过程的影响.
1 基于熵不等式的量子导引度量
自Wisemen 等[5]提出量子导引的具体数学形式以来,发展了多种判定量子导引的不等式以及度量方式,其各有不同的适用范围及判定范围[13].为了度量量子态导引的程度与其参数的关系,本文选择使用基于熵不等式的量子导引度量方式,对Alice 与Bob 共享的某个两体量子态,可以用如下的公式计算量子态的导引[14]:

在量子通讯过程中,有多种不同的量子态可以作为量子通道使用.本文选取几种常用的典型量子通道,基于这些量子通道进行量子通讯过程,并研究这些量子通道的导引与保真度等物理量的关系.
二维Werner 态为[15]

2 保真度公式
保真度能定量地度量量子通讯过程中输入量子态与输出量子态之间的差别,关系到量子信息传递的可靠性,是量子通讯过程中非常关键的物理量.为了计算在量子通讯过程中使用多种量子通道的保真度等物理量,将二维量子态写成泡利矩阵的形式


同时,可以利用量子关联来描述远程量子态制备过程的质量,其表达式为[17]

式中E2和E3为式(7)中的系数.此公式适用于大多数的量子态,能定量地描述量子态的几何关联,是描述量子关联的一种简单、有效的形式.
在标准通道下的量子隐形传态过程中,当输入态为某一纯态|ψ>,通道量子态为二维量子态且包含贝尔态|ϕ+>时,其保真度公式为[20]

式中ρ为隐形传态过程中的通道量子态.而当通道量子态包含其他贝尔态时,将|ϕ+>换作包含的贝尔态即可.此公式计算的是标准通道下的量子隐形传态过程中,遍历所有输入态的保真度的平均值,但仅适用于输入态为纯态的情况.
本文只考虑较为简单的量子通讯过程,将利用已有公式对通道量子态进行计算,并得到相应的结果作比较.
3 结果与讨论
首先,以二维Werner 态即式(3)为例进行计算,根据式(1)可得


同理,利用式(9)计算得其量子关联为
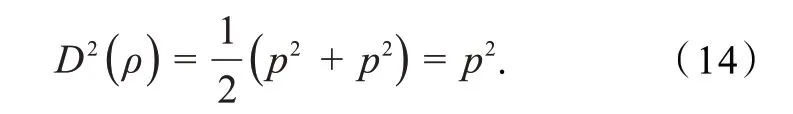
而在标准通道下的量子隐形传态过程中,利用式(10)可得二维Werner 态的保真度为

同样地,也可以计算得到二维Isotropic 态、X态(假定t=1/2)和α态的量子导引、量子关联及保真度.
对上述量子态来说,只有利用式(2)计算得SAB>0 时,量子态才为导引态.因此,相应的量子导引会出现拐点,拐点之后的量子态为导引态,本文重点关注拐点之后量子态的表现.一般来说,当远程量子态制备和量子隐形传态过程的保真度>5/6 时,才具有真正的量子效应.因此,在本文以下的讨论中,利用y=5/6 将对应的线段标注出来,用作与计算得到的保真度的对比,当计算得到的保真度均<5/6时,标注保真度的最大值.
对于远程量子态制备过程,将不同的量子态作为通道时,其量子导引、保真度和量子关联与对应参数的关系如图1 所示. 在远程量子态制备过程中,4 种量子态的导引态(量子导引>0)的保真度和量子关联比非导引态(量子导引<0)更高. 而对于导引态的部分,当量子态的导引性逐渐增强时,远程量子态制备过程的保真度提高,量子关联也同时变强,从而远程量子态制备过程的质量也变高. 因此,通道量子导引对远程量子态制备过程的保真度和量子关联具有正向影响,与远程量子态制备过程的质量同调.
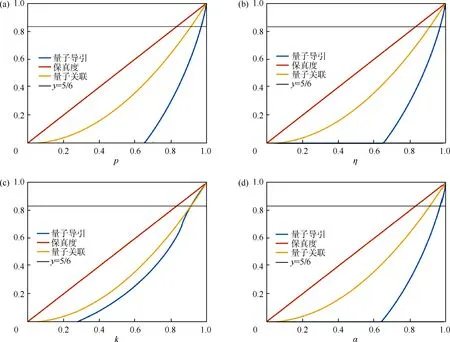
图1 远程量子态制备过程中不同通道量子态的物理量与其系数的关系
对于量子隐形传态过程,将不同的量子态作为通道时,其量子导引和保真度与对应参数的关系如图2 所示. 在量子隐形传态过程中,4 种量子态的导引态(量子导引>0)的保真度比非导引态(量子导引<0)更高. 而对于导引态的部分,当量子态的导引性逐渐增强时,量子隐形传态过程的保真度提高,从而量子隐形传态过程的质量也变高. 因此,通道量子导引对量子隐形传态过程的保真度具有正向影响,与量子隐形传态过程的质量同调.
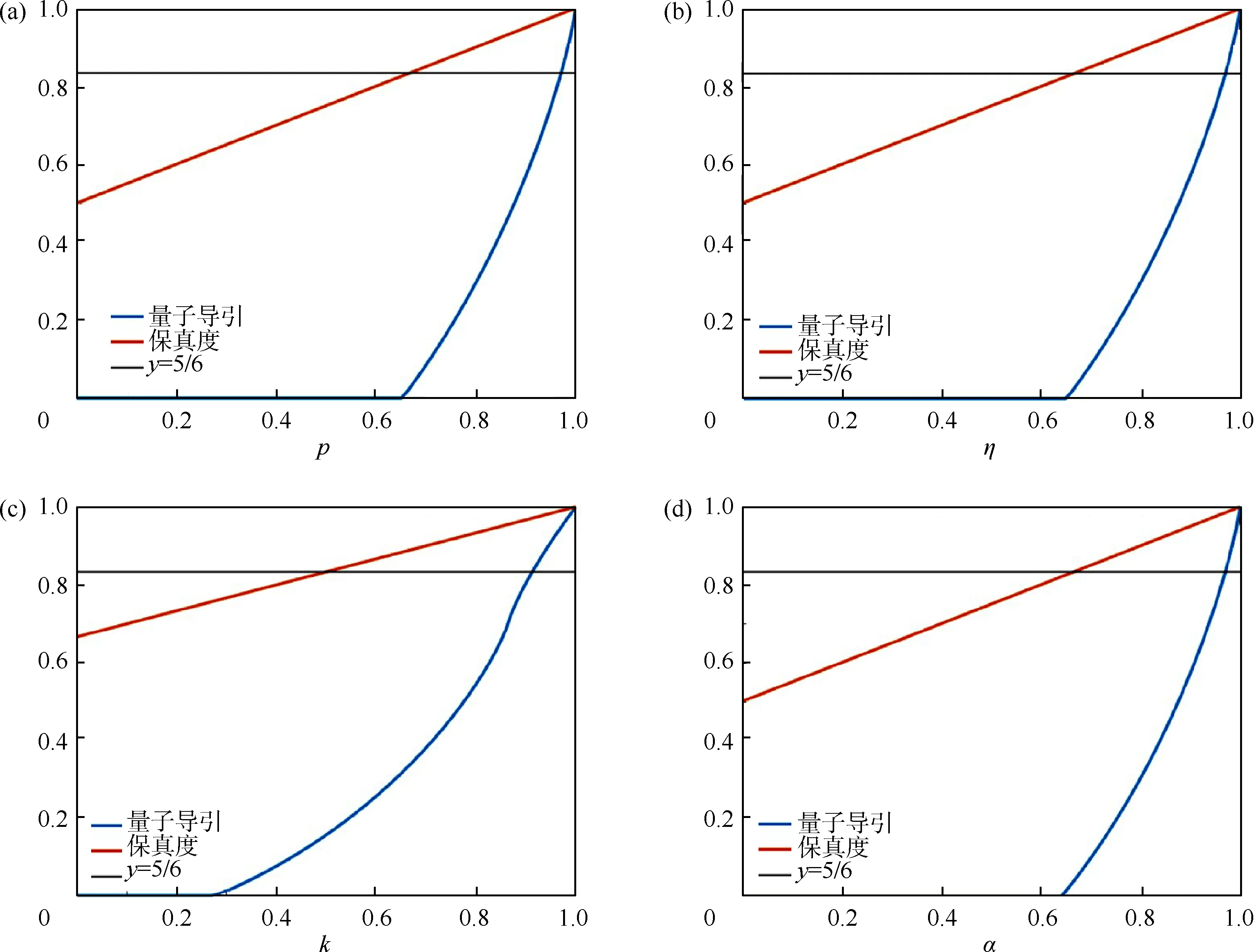
图2 量子隐形传态过程中不同通道量子态的物理量与其系数的关系
4 总结与展望
本文通过计算作为通道的二维Werner 态、Iso‐tropic 态、X 态和α态在远程量子态制备及量子隐形传态过程中通道量子态的量子导引和保真度等物理量,给出了通道量子态的量子导引和保真度等物理量与其参数的对应关系.计算结果表明,通道量子导引对2 种量子通讯过程中的保真度都具有正向影响.通道量子导引对更复杂的量子通讯过程的影响尚需进一步研究,希望这方面的研究结果能够促进量子信息技术发展,也能够让量子导引在量子信息领域有更多的应用.
