基于熵权AHP 修正-TOPSIS 评价模型在选择方面的应用研究

胡嘉峰, 王丽丽

(安徽理工大学数学与大数据学院, 安徽淮南,232001)

随着经济全球化发展, 国内外企业的竞争愈发激烈, 如何在不断发展中使企业处于不败之地, 原材料的采购就是企业竞争的优势之一。企业需要选择最合适的供应商, 而供应商选择问题一直是供应链研究中的热点, 对供应商的评价与选择是供应链中的一个重要环节, 也是供应链管理的重要内容。建筑供应商选择是一个动态的复杂多目标决策问题[1], 文献[2]通过定量分析而选择合作伙伴评估和准测量进行研究; 文献[3]给出了建筑供应链供应商选择的评价指标体系, 对灰色关联度问题和供应商选择模型问题进行探讨; 文献[4]运用TOPSIS 决策模型和熵权法确立最终因子, 构造了加权归一化矩阵, 并得出各方案的贴切度; 文献[5]在基于熵权TOPSIS模型的基础上, 对合作模式下运用模型对选择建筑材料供应商进行研究, 建立了建筑材料供应商指标评价体系, 并用熵权法确定指标的权重比例。用TOPSIS 选择模型对企业供应商进行评价和选择, 许多研究人员都进行了改进, 如将AHP 与TOPSIS[5]和熵权与TOPSIS[6]相结合进行权重计算优化。基于上述模型和方法, 可以发现, 大多数数据模型只考虑基于数据的客观情况, 不可避免地会导致与事实不一致的情况。因此基于该点出发, 本文将对传统的熵权TOPSIS 选择评价模型进行改进, 解决供应商的选择问题。

本文首先建立建筑材料的供应商选择指标评价体系, 基于熵权法初步确定9 个指标的权重因子并进行客观赋权, 再对熵权法的权重作为参考运用AHP 进行适度修正并主观赋权, 得到最终的修正权重后构建TOPSIS 评价模型并对供应商进行排序得出最重要的50 家供货商。最终与未经修正的权重结果进行对比, 证明出熵权AHP 修正-TOPSIS 评价模型最为科学合理。

1 企业供应商选择指标体系的建立

评价指标应当反应被评价对象的特征和属性, 所以选择供应商评价指标体系应该基于系统性、科学性、可测性等原则, 同时将定性指标和定量指标相结合[7]。根据以上原则, 本文通过分析供货商的订货与供货数据, 选取易于度量的指标体系(见表1)。

1.1 数据指标标准化

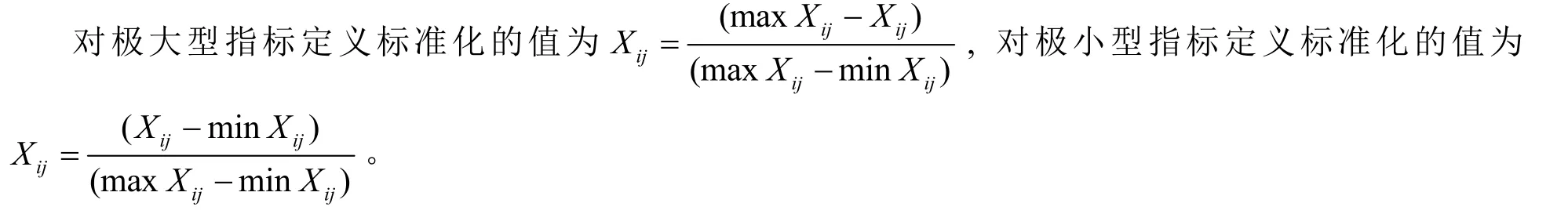
1.2 计算各个指标的熵值

1.3 计算各指标权重

2 建立熵权层次分析修正法

由于熵权法是根据数据自身混乱程度来比较各个指标的权重, 因此缺少主观性。本文通过加强人工干预, 以熵权法计算出的权重作为参考, 运用AHP 进行修正, 并通过修正得出最终的权重。常见的权重评定方法有层次分析法、德尔菲法和熵权层次分析修正法, 其对比见表2 所示。

表2 权重方法特征对比表

由表2 对3 种方法的比较可知, 熵权层次分析修正法能更加科学合理的确定供应商指标权重。运用该方法, 将熵权法得到的9 个指标的权重设置为二级指标, 新定义三个一级指标(绩效评价、战略意义、潜力估计), 算出一级指标的权重, 并通过一致性检验, 结合先前的二级指标的权重得到最终修正后的权重。

2.1 计算修正权重

2.1.1 构造判断矩阵

2.1.2 计算比较矩阵的特征值

将特征向量进行归一化处理作为权向量, 确定各因素的权重。

2.1.3 一致性检验

计算一致性比例CI/RI,当小于1.0 则满足。

计算出绩效评价、战略意义和潜力估计对应的权重分别为40.467%、51.219%和8.314%, 并且通过一致性检验。结合熵权法得到的二级权重, 得到的修正后指标权重。修正前后权重的对比图如图1 所示。

图1 修正前后权重对比图

由图1 可知, 供给弹性在修正前权重相对较大, 因其离散程度较大而在保障生产的重要性中较为次要, 故修正前的权重与实际情况矛盾。而修正后的供给弹性权重相对较小, 符合实际情况。供应量方差在修正前并未考虑, 修正后的权重给予考虑。因此, 修正后的权重更加科学合理。

2.2 建立最终TOPSIS 评价模型

TOPSIS 方法[10]即理想点法, 又称近似理想解排序法, 是一种方便有效的多目标决策分析方法, 按照问题的理想解和负理想解进行排序。理想解是方案中未存在的虚解, 指标值应与各方案的理想值一致。负理想解是方案的最差解, 指标值应是每个方案的最小理想值。TOPSIS 法通过标准化的数据矩阵,在多个目标中寻找理想解和负理想解, 通过计算评价目标与理想解和负理想解之间的距离, 然后进行距离的比较。最接近理想解并且最远离负理想解的方案是最佳方案。具体步骤如下:

(1) 将最终修正的指标权重数据导入到TOPSIS 模型中, 进行归一化处理, 并将归一化处理后的数据进行加权。

3 实验分析

3.1 数据描述

该研究数据来源于2021 年全国大学生数学建模竞赛。

(1) 企业订单数量: 第1 列为供应商名称, 第2 列为供应商供应的原材料类别, 第3 列和第4 例为企业每周向各供应商的订货量(m3)。值“0”表示所在对应的周企业没有向相应供应商订货。

(2) 供应商供应数量: 第1列为供应商名称, 第2列、第3列和第4列为各供应商每周供应量(m3), 值“0”表示所在对应的周供应商没有向企业供货。部分数据见表3 和表4。

表3 企业的订货量

表4 供应商的供货量

3.2 实验结果

表5 为未进行修正得出的最重要的50 家供应商信息排名结果分布表。

表5 未修正的结果分布

续表5

表6 为根据本文的方法得出的最重要50 家供货商[11]修正后的排名结果分布表。

表6 修正后结果分布

由表5 和表6 可知, 表5 在S108 后出现了明显的断层现象, 这是由于极大和极小指标选取造成的。而表6 其重要性程度分布均匀, 并且排名在前的供应商大多2 个或2 个以上指标表现出色, 或者大部分指标表现良好, 符合实际情况。S201 在表6 中排名第1 而在表5 中排名明显靠后, 基于对S201 的指标数据分析, 发现S201 供货量具有周期性, 会随季度影响而出现淡季和旺季, 而未修正的模型中并没有考虑到实际情况而导致偏差, 因此本文的模型更具有可行性。

4 结论

该模型在熵权法的基础上运用层次分析法赋权从而兼顾主观性与客观性, 使权重具有确定性和非确定性的特点。既解决了传统指标选择的单一问题, 又简化了靠近理想解排序法指标过多的问题, 从而提高了供货商选择的准确性, 强化了选择评价过程的科学性和合理性, 符合现实生活中的应用, 可以为各种选择问题提供参考依据。