基于混合效应的华北落叶松次生林单木冠长模型

夏 杰，周根苗，易 烜，王盼琦，吕 勇

（1. 中南林业科技大学 林学院，湖南 长沙 410004；2. 湖南省农林工业勘察设计研究总院，湖南 长沙 410007；3. 湖南省青羊湖国有林场，湖南 宁乡 410600）

树冠是林木进行光合、呼吸以及蒸腾作用等生理代谢的重要场所[1-2]。树冠大小与树木的生长潜力密切相关[3]，同时，树冠大小也能反映树木长期的竞争水平[4-5]。冠长是反映树冠大小及其垂直结构的重要指标，其常作为协变量应用于林木生长模型，用来预估树高、胸径生长量以及反映树木枯损等[4]。此外，冠长也是树冠上部进行外轮廓模拟与可视化的重要参数，可为树种识别提供树木冠形特征[6]。

考虑到林地条件和林分结构的复杂性，对冠长的大面积实地调查耗时费力。因此，国内外学者通常通过建立统计模型对其进行预测[7-8]。目前对冠长的研究常使用胸径作为自变量，通过线性或非线性回归进行预测[9]。一般地，使用回归方法构建模型，误差项（ε）需要满足独立、等方差且服从正态分布[10]。然而，林业数据通常在空间和时间上是自相关的[11]，上述假设往往不成立，从而导致对参数标准差的有偏估计[12]。非线性混合效应模型是一种参数受随机变量影响的回归模型，可以同时估计群体的平均效应和个体差异[13]。作为混合效应（线性、非线性）模型之一，非线性混合效应模型能够灵活有效地分析分组数据（纵向数据、重复观测数据、分块设计数据以及多水平数据等[14]），因此，其已被广泛应用于林木生长发育的拟合与预测。符利勇等[4]考虑到立地指数和样地对冠幅生长的随机影响，以湖南省黄丰桥国有林场的103 块杉木标准地为研究对象，构建了嵌套两水平非线性混合冠幅模型；Wang 等[10]发现以竞争指数（包括与距离有关的竞争指数、与距离无关的竞争指数）作为随机效应构建的杉木冠幅、冠长混合效应模型与基础模型相比，模型精度得到显著提升。

华北落叶松Larix principis-rupprechtii是我国独有树种，是华北地区针叶林带的主要树种[15-16]。因此对华北落叶松的研究尤为重要。但是目前关于华北落叶松次生林冠长的研究极少，尤其是应用非线性混合效应模型的研究更是寥寥无几[17]。然而这种模型相比传统模型具有很大的优势，本研究有助于预测华北落叶松的树木生长，能够为华北落叶松的生产、经营提供理论依据。

1 研究区概况

研究对象为华北落叶松次生林，研究区选择在山西省五台山伯强林场和关帝山庞泉沟国家级自然保护区两个华北落叶松次生林主要分布区。

山西省关帝山庞泉沟国家级自然保护区位于吕梁山脉中段，是华北第二高峰，位于111°22′～111°33′E、37°45′～37°55′N 之间，属暖温带及吕梁山半温润区。保护区内自然资源丰富，森林覆盖率高达86%。

五台山伯强林场位于“摔跤之乡”山西省忻州市，是中国四大佛教名山之一，介于112°50′ ～113°50′E，38°30′ ～39°15′N 之 间，属太行山系北端。五台山伯强林场属暖温带半湿润季风气候，森林群落主要由木本植物-乔灌木组成。华北落叶松是五台山地区的主要针叶林树种，多分布于半阴坡、阴坡，次生林以五台山北坡尤为集中[18]。

2 材料与方法

2.1 数据来源及处理

数据采集时间为2015 年7—9 月，数据采集地点位于山西省关帝山庞泉沟自然保护区和五台山伯强林场，在华北落叶松次生林集中分布区中选择无明显人为破坏及自然灾害的地块，根据不同的海拔和立地类型随机布设样地，共布设116 块20 m×20 m 华北落叶松次生林调查样地，其中关帝山庞泉沟自然保护区调查2 块100 m×100 m 固定样地（细分为50 块20 m×20 m 小样地），17块20 m×20 m 临时样地，共67 块20 m×20 m 调查样地；五台山伯强林场调查1 块100 m×100 m固定样地（细分为25 块20 m×20 m 小样地），24 块20 m×20 m 临时样地，共49 块20 m×20 m调查样地。

实测样地内各林分因子和立地因子。对于胸径≥5 cm 的林木进行每木检尺，实测其树高（0.1 m）、胸径（0.1 cm）和枝下高（0.1 m），其中枝下高及树高选用高精度超声波测高仪来测量。共调查华北落叶松次生林单木2 745 株，1 307 株位于关帝山庞泉沟自然保护区，1 438 株来源于五台山伯强林场[18]。

在所调查的116 块样地的2 745 株单木数据中，按4∶1 比例随机选取建模数据和检验数据，其中2 196 株单木数据作为建模数据，其余的549 株单木数据作为检验数据，各林木、林分因子见表1。

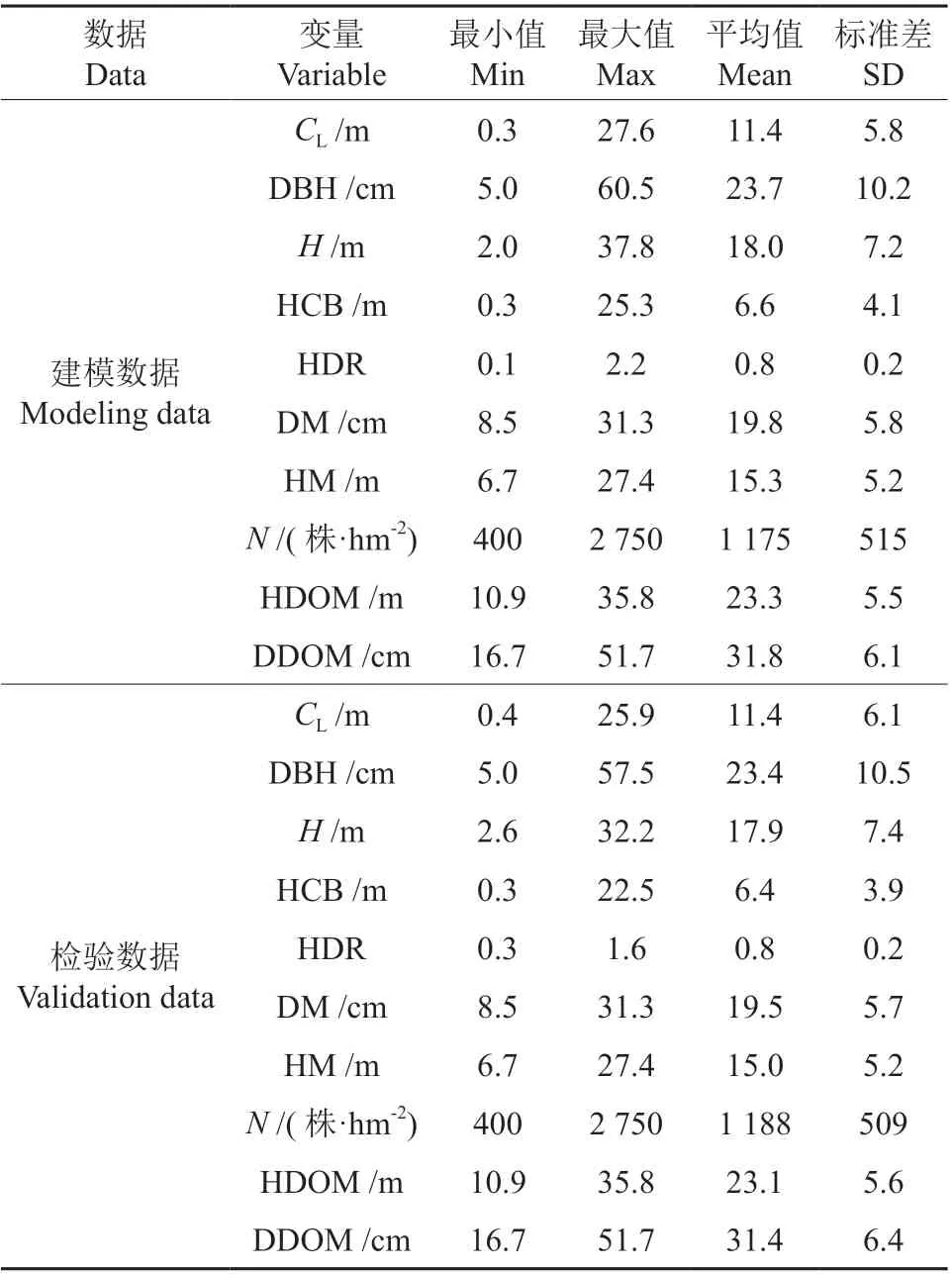
表 1 建模和检验数据变量因子信息†Table 1 Modeling and validation data variable factor information

2.2 研究方法

2.2.1 基础模型的选择

选择9 个常用的冠长-胸径模型作为候选模型（表2），利用拟合评价指标比较各候选模型的拟合效果与检验结果，从9 个候选模型中挑选出拟合精度最优、拟合误差最小的候选模型作为华北落叶松单木冠长的最优基础模型。

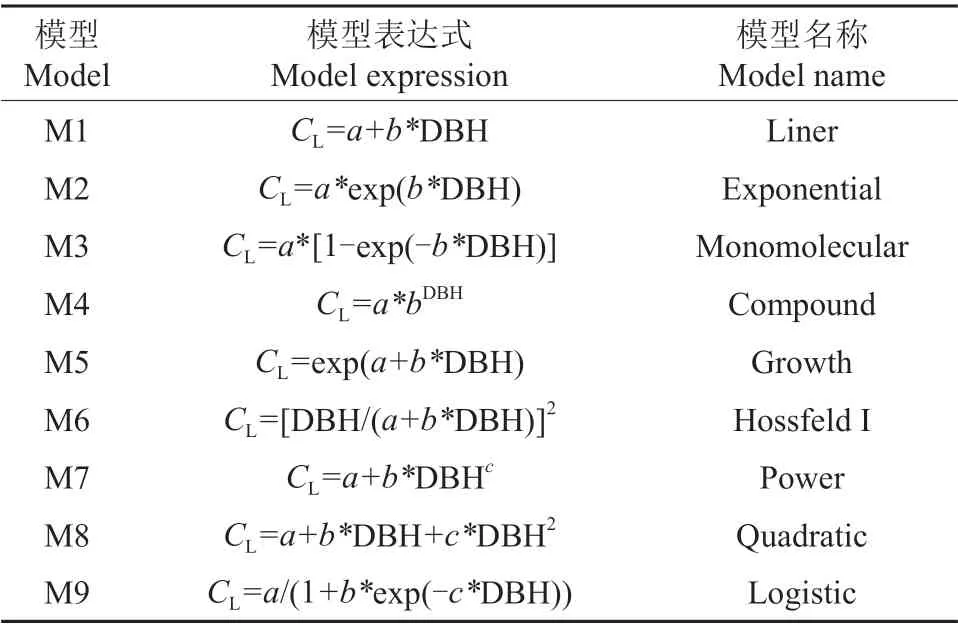
表2 9 个冠长-胸径单因子候选模型†Table 2 Nine candidate single factor models of crown length-diameter at breast height

2.2.2 协变量的筛选

在现实林分中林木冠长不仅仅只受胸径的影响，同时还会受到其他林木、林分因子的影响，因此本研究把这些因子作为协变量加入到上述选定的基础模型中，能够更好地提高模型精度且具有更好的生物学解释。利用SPSS 25.0 软件对其他各项林木、林分因子进行逐步回归分析，根据方差膨胀因子（VIF）剔除共线性严重（VIF ＞5）的因子，从而保留共线性弱且影响显著的因子[19]。采用再参数化方法，将显著因子引入到最优基础模型中，考虑显著因子在最优基础模型中的组合形式多样，对不同组合形式的再参数化模型进行比较分析，最终选择拟合效果最好的模型作为最优的华北落叶松再参数化（多变量）模型。

2.2.3 混合效应模型

混合效应模型有两种形式，一是线性混合效应模型（Linear Mixed Effects Model，简称LME），二是非线性混合效应模型（Nonlinear Mixed Effects Model，简称NLMES）[20]，目前这一方法被广泛地应用在生产、生活的各个领域中。林木生长发育过程在不同样地上具有显著的差异。在以往模拟林木林分因子时，建立的模型基本上都没有考虑到样地水平上的影响。因此本研究在充分了解混合效应模型原理方法的基础上，运用华北落叶松单木冠长数据建立含样地随机效应的单木冠长混合效应模型[21]。

确定再参数化模型后，进一步考虑样地对单木冠长的随机影响，本研究拟采用样地单水平的非线性混合效应模型[22]。

混合效应的一般表达式如下：

式中：yi与xi分别为第i个样地的因变量向量和自变量向量；λi为误差项；α与δi分别为固定效应参数向量和随机参数向量。

2.2.4 模型评价

利用R 语言软件对模型进行拟合，求解模型参数以及模型的评价指标。本研究采用确定系数（R2）、平均绝对误差（MAE）、均方根误差（RMSE）、赤池信息准则（AIC）及贝叶斯信息准则（BIC）对各个模型进行评价。

2.2.5 模型异方差

混合效应模型在参数效应和随机效应的方差协方差结构确定后，有两个问题必须要考虑：一是模型的异方差，二是数据的自相关性[23]。由于本研究的数据不是重复观测的单木冠长数据，故不需要考虑时间序列的相关即自相关性。通过观察模型残差图是否具有明显的喇叭状来判断其异方差性。误差方差协方差结构经常用到的有3 种形式，分别是指数函数（Var Exp）、幂函数（Var Power）和常数加幂函数（Var Const Power）[24]。

3 结果与分析

3.1 华北落叶松单木冠长基础模型的确定

基于R 语言软件NLS（Nonlinear Least Squares）函数对表2 中9 个候选模型分别进行拟合，将建模数据代入各个候选模型中，得到评价指标，对各评价指标进行比较分析。从表2 中可以看出，9 个候选模型可以分成两参数和三参数两部分。从表3 可知三参数中R2最高的为M9，两参数中R2最高的为M6，运用R 语言软件中的方差分析（ANOVA）对M6 与M9 这两个模型进行方差分析，判断这两种模型间是否具有明显的差异，如果有显著差异，说明参数适当增加会使模型更具有意义。本文中M6 与M9 的方差分析结果为F=32.831，P＜0.001，可知两个模型的差异性为显著，且具有三参数的模型M9 的确定系数（0.569 9）高于两参数模型M6（R2=0.563 4）；模型M9 的均方根误差（RMSE=3.812 7）小于M6（RMSE=3.841 3），模型M9 的平均绝对误差（MAE=3.022 3）小于M6（MAE=3.062 2），因此选择具有三参数的M9作为冠长模型的基础模型，公式为：

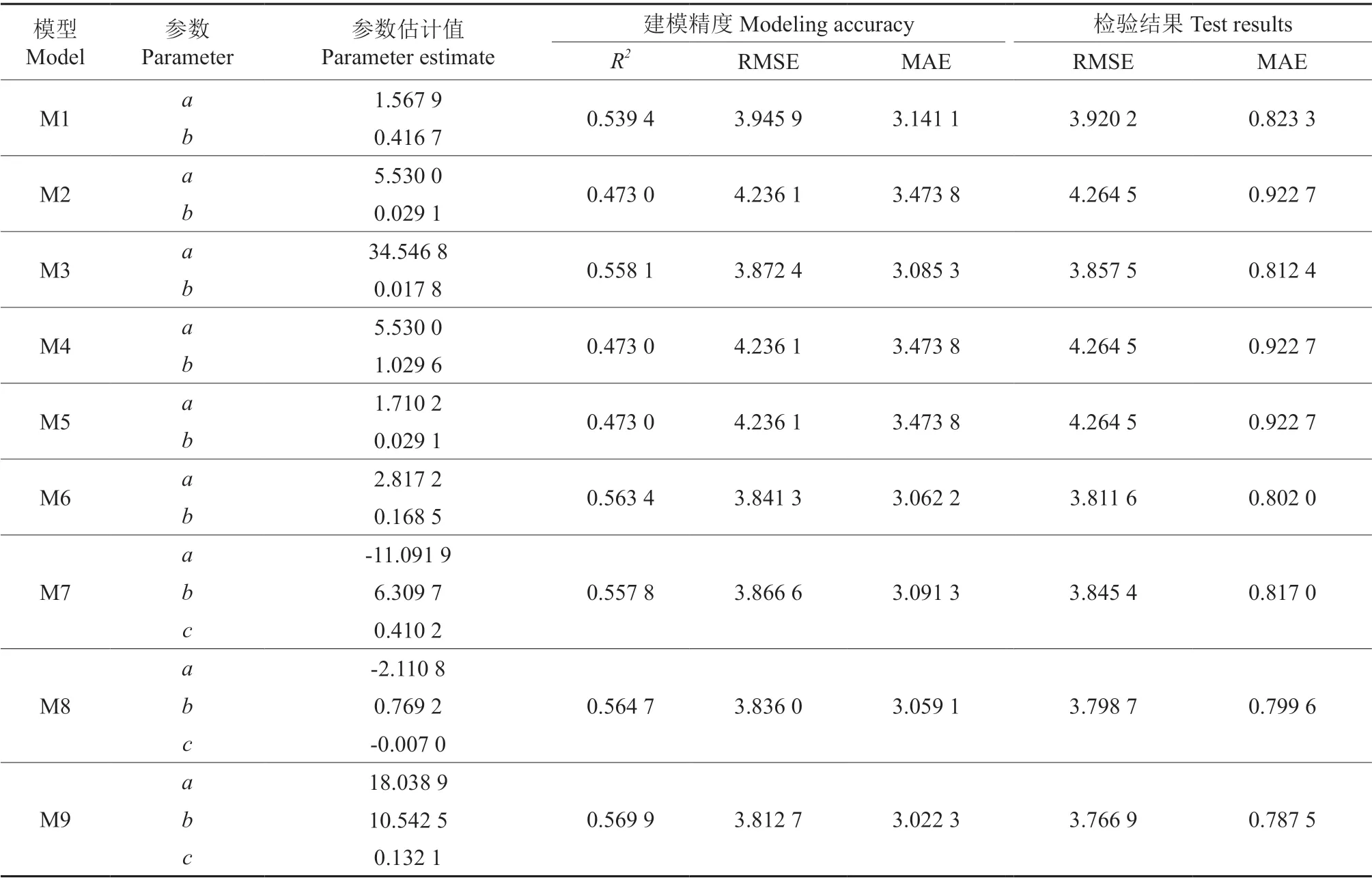
表3 各候选模型参数值及评价指标Table 3 Parameter values and evaluation indicators of each candidate model

CL=18.038 9/[1+10.542 5exp(-0.132 1DBH)]。（7）

3.2 华北落叶松单木冠长多变量模型的构建

利用SPSS 25.0 软件的线性分析对各林木、林分因子进行逐步回归分析，正常情况下模型的参数越多精度就会越高，本研究为了防止模型的过参数化，本着少因子、高精度、不共线的原则，选取方差膨胀因子（VIF）小于5的变量作为协变量（表4），选取了高径比（HDR）、公顷株数（N）作为协变量加入基础方程，通过R 语言软件的NLS 函数将各种组合方式分别进行拟合（表5），对比分析可知模型M9-6 在再参数化模型9 个组合方式中拟合效果最好，得出最佳拟合形式，结果见式（8），模型确定系数R2从0.569 9 上升到0.700 5，均方根误差RMSE 从3.812 7 下降到3.181 6，平均绝对误差MAE 从3.022 3 下降到2.410 7（表6）。

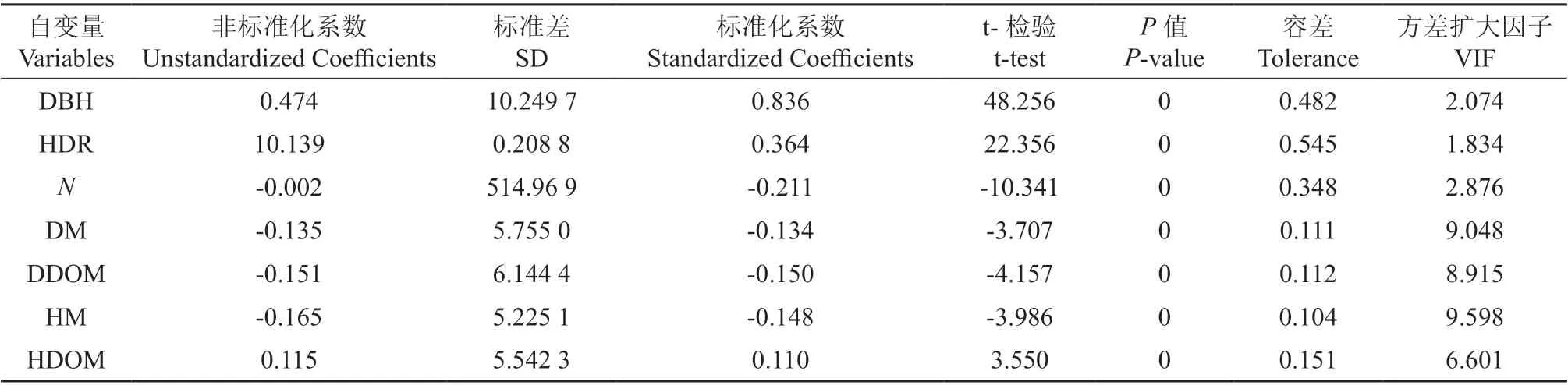
表4 模型中其他协变量的筛选Table 4 Selection of other covariates in the model

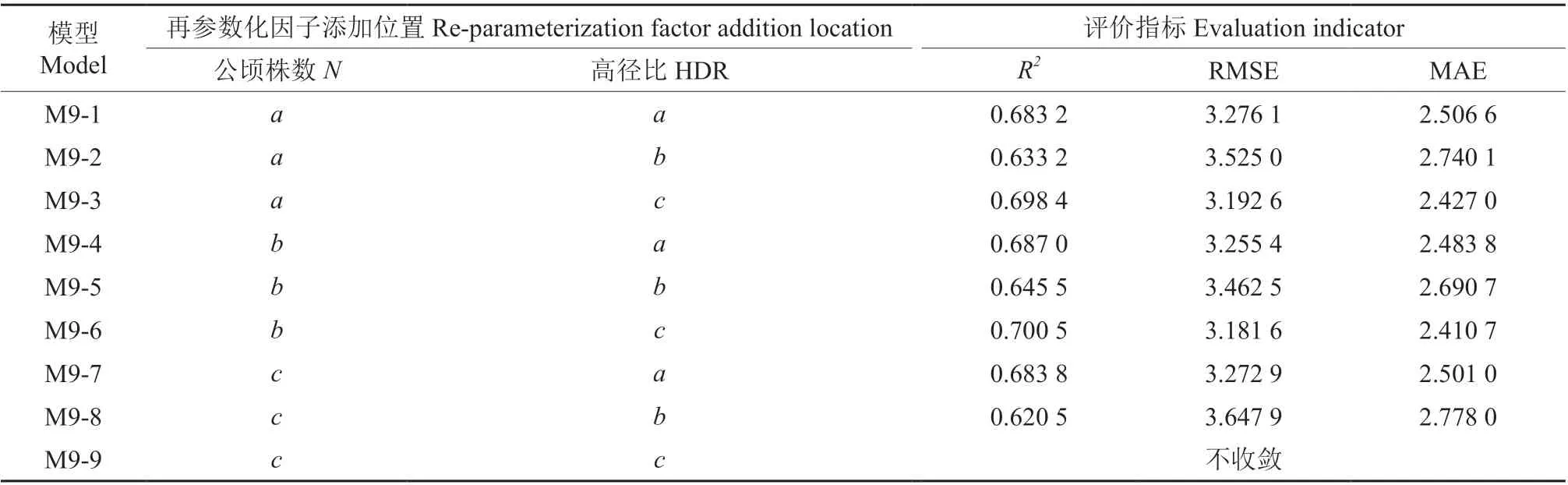
表5 再参数化不同组合形式的模型精度Table 5 Re-parameterizing different combinations of model accuracy

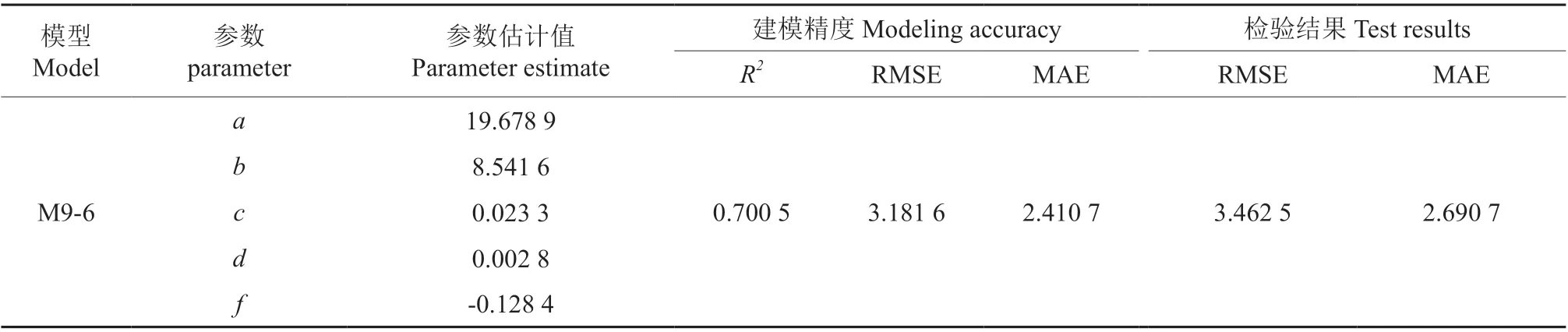
表6 模型M9-6 各参数值和评价指标Table 6 The parameter values and evaluation indexes of model M9-6

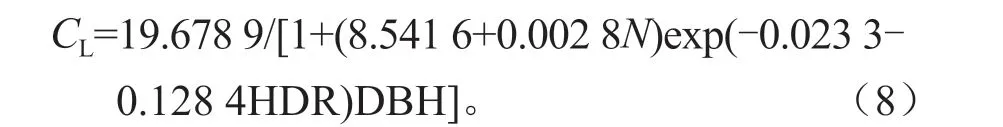
式中：CL为冠长；N为样方公顷株树；HDR 为树高和胸径之比；DBH 为胸径。

3.3 华北落叶松单木冠长混合效应模型的构建

考虑到本研究数据来源于116 块样地，本研究拟采用样地单水平作为随机因子来构建华北落叶松次生林单木冠长非线性混合效应模型，利用R 语言软件的NLME（Nonlinear Mixed-Effects Models）函数包对各组合形式的模型分别进行拟合，比较分析各组合形式非线性混合效应模型的评价指标（表7）。为了防止模型过度参数化，最终选定样地水平随机效应作用在固定参数a上（M10-1），详见式（9），该模型的精度最高，模型确定系数R2从0.700 5 提升到0.813 6，均方根误差从3.181 6 下降到2.512 0，平均绝对误差从2.410 7 下降到1.837 3（表8）。

表7 各混合效应组合形式拟合效果Table 7 Fitting effect of various mixed effect combinations

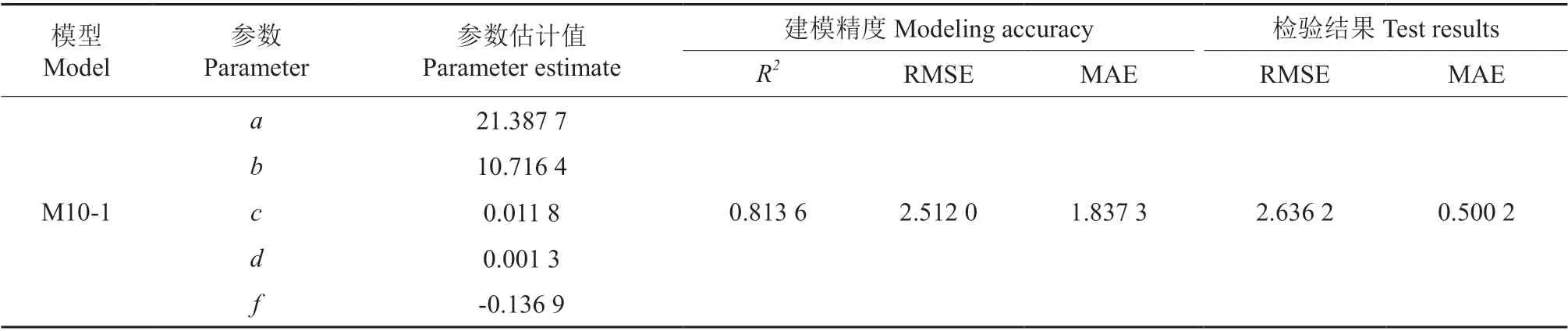
表8 模型M10-1 各参数值和评价指标Table 8 The parameter values and evaluation indexes of model M10-1

表9 各模型的参数值与评价指标Table 9 Parameter values and evaluation indexes of each model

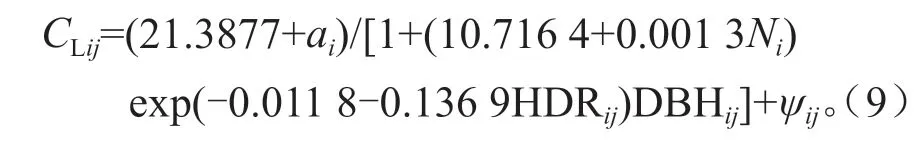
式中：CLij为第i个样方中的第j株的单木冠长；Ni为第i个样方的公顷株数；HDRij为第i个样方第j株单木高径比；DBHij为第i个样方第j株的单木胸径；ai为第i样方的随机效应参数；ψij为第i个样方第j株单木的误差项。

3.4 模型评价

绘制基础模型M9、再参数化模型M9-6 和混合效应模型M10-1 的残差图（图1），3 个模型的残差值都较为均匀地分布在X轴两侧，可以看出从基础模型到再参数化模型再到混合效应模型，模型的残差值分布得更加均匀且聚集在-2 到2 之间。

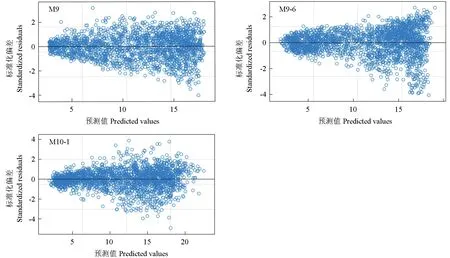
图1 各模型的残差分布Fig. 1 Residual distribution of each model

对基础模型（M9）、再参数化模型（M9-6）和混合效应模型(M10-1)进行比较分析，结果见表9。由表9 可知，模型的确定系数（R2）从基础模型M9 的0.569 9 提升到再参数化模型M9-6的0.700 5 再到混合效应模型M10-1 的0.813 6，提高了42.8%；模型的均方根误差从3.812 7 降低到3.181 6 再到2.512 0，降低了34.1%；模型的赤池信息准则从12 024.17 降低到11 239.63 再到10 564.37，降低了12.1%；模型的贝叶斯信息准则从12 046.92 降低到11 273.75 再到10 604.18，降低了12.0%，可以说明混合效应模型能够有效地提高冠长模型的精度。

3.5 混合效应模型异方差及其处理

通过混合效应模型（M10-1）的残差图（图2）可以看出，模型有明显的喇叭状，即有异方差性。本研究采用上述3 种常用的方差消除函数改善混合效应模型的异方差性，3 种形式的方差函数各评价指标结果见表9。从表10 可以看出，各评价指标都说明指数函数M11 优于幂函数M12 和常数加幂函数M13。从残差分布（图2）对比可以看出，加入上述3 种函数模型的残差值的分布均显示更为均匀，尤以指数函数M11 的残差分布图变化比较明显且显示得更为均匀地分布在X轴的两侧。

表10 以模型M11 为基础的考虑不同异方差函数的模拟结果Table 10 Simulation results of different heteroscedasticity functions are considered based on Model M11

图2 各模型的残差分布Fig. 2 Residual distribution of each model

4 结论与讨论

4.1 讨 论

冠长是描述树冠垂直结构、反映林木竞争的重要指标，构建冠长-胸径模型预测林木冠长对了解林分树冠结构、林分生长潜力具有重要意义。对于冠长-胸径模型的构建，国内外学者通常从常见的冠长模型中选取一个较好描述冠长与胸径关系的模型作为基础模型，然后，在此基础上引入对冠长生长影响显著的协变量（气候因子、土壤因子、地形地貌因子、林分因子[25-27]等），从而使得模型的精度更高，适用性更广。

本研究从9 个候选的冠长-胸径模型中，选取拟合精度最高（R2=0.569 9）、误差最小（RMSE=3.812 7，MAE=3.022 3）的Logistic 模型（M9）作为最优基础模型，其不仅具有良好的生物学解释，而且具有较好的适用性，与段光爽等[18]的研究结果一致。

为了改进冠长-胸径模型的预测精度，本研究还考虑了除胸径以外其他6 个林木、林分因子对冠长生长的影响。为了避免模型中变量过多导致模型参数增加，进而影响模型计算不收敛，采用逐步回归分析对6 个因子进行了显著性筛选。研究发现对象木高径比及其所在林分的公顷株数对冠长的影响最为显著。采用再参数化方法，将高径比、公顷株数引入Logistic 模型（M9），共有9 种组合形式，结果显示：分别将高径比、公顷株数加到最优基础模型参数c、b上，模型拟合效果最好，最优再参数化模型为M9-6。通过模型M9-6 的数学方程式可以看出冠长和公顷株数呈负相关关系，即随着林分密度的增长，林木的冠长会降低，这与刘学锋等[28]的研究结果一致，这一结论可以指导人工林的初值密度和抚育间伐时间。冠长和高径比也有一定的关联，即冠长可以反映木材的干形和木材品质。

在最优再参数化模型M9-6 的基础上，本研究引入了样地作为随机效应，构建了基于样地单水平的华北落叶松单木冠长混合效应模型，模型性能得到显著提高。研究发现，混合效应模型能有效提高树冠结构模型的精度。李春明等[29]在对比传统的回归模型方法与混合模型方法构建落叶松云冷杉林分断面积模型之后，得出混合模型方法精度更高的结果，说明运用混合模型方法能够有效地提高模型精度。符利勇等[4]通过引入立地指数和样地作为随机效应，提高了模型对杉木冠幅的预测精度。Wang 等[10]通过引入竞争指数（与距离无关、与距离有关）作为随机效应，同时提高了对冠幅与冠长的预测效果。

许多研究证明，引入随机效应可以纠正或减少自相关性和异方差[30]，在本研究中也发现了类似的结果。此外，本研究进一步引入了3 个方差函数来减少华北落叶松单木冠长混合效应模型的异方差性，结果发现降低残差异方差的最优函数是指数函数，这与Calama 等[31]的研究结果一致。本研究中未考虑到竞争以及气候等因子对冠长生长的影响，后续的研究中将会进一步考虑到林木间的竞争和气候对冠长的影响。

4.2 结 论

本研究以山西省116块样地的2 745株华北落叶松次生林为研究对象，比较9个冠长-胸径候选模型，选定Logistic 形式为最优基础模型（R2=0.569 9，RMSE=3.812 7，MAE=3.022 3）；考虑到现实林分中冠长不仅仅只受到胸径的影响，通过逐步回归分析加入高径比和公顷株数，比较不同的组合形式，最终确定M9-6 为最优拟合形式（R2=0.700 5，RMSE=3.181 6，MAE=2.410 7）；最后引入样地随机因子到再参数化模型，通过比较分析得到最佳拟合形式为样地随机因子作用在固定参数a上，加入样地随机因子的模型精度有了显著的提升（R2=0.8136，RMSE=2.5120，MAE=1.8373）。研究结果说明了样地对冠长的影响显著，为不同立地对冠长生长影响的合理性提供了支撑，其在提高精度的同时，也有利于指导华北落叶松区域性的森林经营，且本文的研究对象是单木，更具有实际应用价值。