基于新的参考光滑性指示子的改进的三阶WENO格式*

王亚辉

（郑州师范学院 数学与统计学院，郑州 450044）

引 言

可压缩流的数值求解是计算流体力学的主要研究内容之一.求解可压缩流Euler方程往往就是求解非线性双曲守恒律方程，其解往往会伴随一些比较复杂的流动，比如包含间断和光滑小尺度结构.在不产生虚假振荡的情况下捕捉间断，并尽可能多地求解小尺度结构，是数值格式的必要条件.在模拟复杂流动问题时，高精度阶方法往往比低精度阶方法的计算效率和效果要优越得多.在众多求解双曲守恒律的高精度数值格式中，加权本质无振荡(WENO)格式已成为最受欢迎的方法之一.WENO格式通过一组动态候选模板的低阶多项式的非线性组合来达到抑制虚假数值振荡的目的.其中加权过程是根据每个候选模板的光滑度评估其局部通量的贡献来执行的，具体地说，WENO格式中的光滑度指示子可以使格式向最优方向发展，并通过分配间断模板的基本零权重来避免跨间断的插值.

Liu等首先提出了WENO格式[1]，其主要构造思想是给出所有候选子模板的非线性权来凸组合ENO格式[2-5]来提高解在光滑区域的精度，而且在间断附近不会发生明显的振荡，即保持ENO格式的特性.该过程根据候选模板上解的光滑性指示子对局部数值通量的贡献进行加权来执行，使得包含间断的局部数值通量的模板权重基本上为零.然而，Liu等所提出的WENO格式有明显的缺点，即数值格式无法得到最优收敛精度阶.Jiang和Shu[6]解决了这一问题，并设计了一个新的光滑性指标子的计算方法，即所有低阶多项式的各阶导数的L2范数的归一化平方和，从而提出了经典的有限差分WENO(WENO-JS)格式.Henrick等[7]通过数值分析WENO-JS格式的各候选模板光滑性指示子发现，WENO-JS格式在具有一阶临界点的光滑区域无法保持最优的收敛精度阶，进而提出了WENO-M格式，用映射函数修改了非线性权，给出了使之满足格式最优收敛精度阶的充要条件.Borges等[8]发展了WENO-Z格式，该方法将全局模板高阶光滑性指示子纳入非线性权重的构造中.WENO-Z格式可以达到与WENO-M格式相同的收敛精度.由于该格式赋予间断模板较大的权重，所以该格式具有高分辨率与低耗散特性.文献[9]将WENO-Z格式推广到十一阶WENO格式，发展了七阶到十一阶WENO-Z格式.近几年来，许多学者又发展了具有高分辨率高精度的改进的WENO格式[10-11].

对于三阶WENO格式来说，虽然没有高阶WENO格式那么好的分辨率，但其仍然具有许多优点.比如，求解带有激波问题时具有很好的鲁棒性，并且使用网格点的规模较小，从而降低了边界处理和求解的难度，易于推广到非结构网格上.尽管三阶WENO格式具有以上的优点，但是很多学者仍不会采用它，主要的原因是经典的三阶WENO格式在光滑区域的精度在二到三阶之间，而在有临界点的区域退化为一阶精度.另外，由于三阶WENO格式计算成本较低，是比较理想的数值格式.恢复经典的三阶WENO格式的最优收敛精度阶和提高其分辨率成为了许多学者研究的方向，大多情况下利用WENO-Z格式的加权过程，可以解决提高分辨率和恢复最优收敛阶的问题.采用这种途径，Wu和Zhao[12]给出了一个改进的三阶WENO格式(WENO-N3).通过对候选模板的光滑度指示子与全局模板的光滑度指示子进行线性组合，设计了一个具有四阶精度的参考性光滑度指示子 τ4N.然而 τ4N不能使格式在临界点附近达到最优三阶收敛精度.为弥补这个缺陷，Wu等[13]用τ4Np的p幂形式改进了参考光滑度指示子，得到了WENO-Np3格式.最近，Xu和Wu[14]提出了另一个四阶参考光滑度指示子τ4P，这样得到的WENO-P3格式的耗散性更小.然而，该算法也只能在没有临界点的光滑区域实现三阶精度，在有临界点的光滑区域降到一阶准确度.在文献[15]中，笔者给出了三阶WENO格式的参考光滑度指示子 τ4Rp，理论分析表明，所得到的WENO-Rp3格式(p=1．5)在光滑区域(包括临界点)能达到三阶精度，并且WENO-R3格式(p=1)保持了ENO性质.在文献[16]中，笔者提出了一种修正模板的三阶WENO格式，通过改进经典WENO-JS3格式中各候选模板上数值通量的一阶多项式逼近，并加入二次项使模板逼近达到三阶精度，并且计算了新的数值通量，使新发展的格式(WENO-MS)在光滑区域(包括一阶临界点)具有三阶收敛精度，并且还通过引入一个可调函数 φ0使WENO-MS格式具有ENO特性.关于三阶WENO格式的其他改进格式可参考文献[17-18].

为了提高经典三阶WENO格式的计算分辨率和数值收敛精度，本文提出了一种新的全局参考光滑度指示子的计算方法.这里所采取的主要策略与文献[8]不同，它是通过候选子模板上重构多项式的导数的线性组合与整个全局模板上重构多项式的导数的L2范数逼近来计算得到的.其中会引入一个介于0和1之间的自由参数φ，通过调节该自由参数的值，可以获得不同的参考光滑性指示子，并且所获得的参考光滑性指示子的阶数比WENO-Z格式的更高.当自由参数取某些特定的值时，我们可以得到之前发展的三阶WENO格式[12-13].最后本文给出了一系列一维和二维数值算例验证新格式(WENO-Re3) 的性能.数值结果表明，与WENO-JS3、WENO-Z3和WENO-P3格式相比，WENO-Re3格式对精细光滑结构具有相当或更高的分辨率.

本文主要安排如下：第1节通过一维标量守恒律方程简要的回顾了三阶WENO格式；第2节提出了新的参考光滑度指示子的计算方法，并给出了WENO-Re3格式；第3节通过一系列一维和二维数值算例来说明了新格式的性能；第4节对全文进行了总结.

1 三阶WENO格式综述

在本节中，首先通过一维标量守恒律简要介绍一下三阶WENO有限差分格式：

1.1 三阶WENO格式

它们结合起来定义了格式的数值通量

这里的非线性权重ωk定义为

其中，常系数dk被称为理想权重，因为它们与的 线性组合保持最优三阶收敛到h(xj+1/2)，即

dk的具体值如下所示：

式(9)中的 0 ＜ϵ≤1是 为防止被零除而引入的小正参数， βk是第k个模板的光滑度指示子.Jiang和Shu[6]提出的光滑度指示子为

其具体形式为

Borges等[8]提出了一个WENO-Z权：

其中 ϵ =10-40，τ3=|β1-β0|是 一个三阶参考光滑探测子，它驱使非线性权重ωk(13)向最优权重dk靠近，并且比JS权重(9)快.当幂q=2时，WENO-Z格式在一阶临界点处可以达到最优的三阶，但在间断附近具有更多的耗散，一个不那么耗散的方法是设计一个足够的高阶参考光滑探测子，并且总是使用幂q=1.

为了为WENO-Z权设计一个合适的参考光滑探测子(13)，需要一个充分条件来恢复三阶WENO格式的最优阶精度.在文献[14]中，给出了三阶WENO格式达到三阶精度的一个充分条件：

方程(14)仅仅是一个充分条件，但不是必要条件.然而，这一条件为设计高阶参考光滑性指示子提供了有用的信息.

2 新的全局参考光滑性指示子

在本节中，我们为三阶WENO格式提出了一个新的参考光滑性度指标子 τ4Re.此参考光滑度指标子的构造策略是每个候选模板的重构多项式的一阶导数的线性凸组合与全局模板的重构多项式的一阶导数的L2范数逼近的平方和，与参考光滑性指标子 τ4P[14-15]相比，在数量上具有较少值，并且在光滑区域同样具有四阶精度.

首先，我们给出图1中候选子模板和全局模板的重构多项式，其重构多项式具体形式如下：

图1 三阶WENO数值通量的模板Fig.1 The stencils for the 3rd-order WENO numerical flux

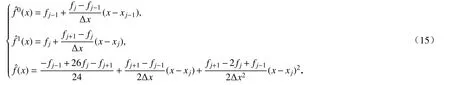
注1对式(16)进行简单地积分消参运算，可以得到全局参考光滑性指示子的表达式为

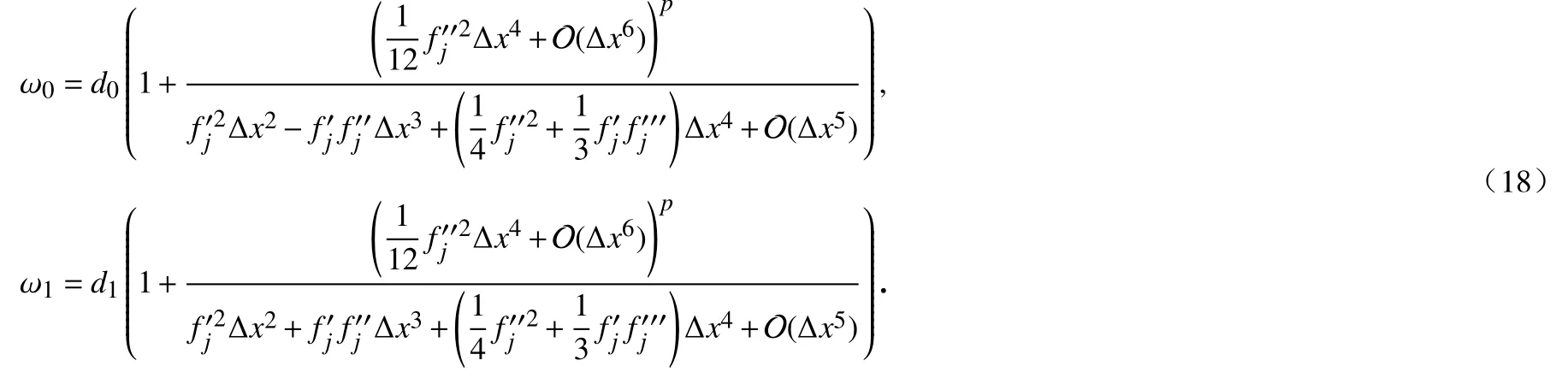
根据和的取值不同，可以分为如下两种形式：

通过式(19)与充分条件(14)相比，当p=1时，能够得出WENO-Re3在没有一阶临界点的光滑区域能实现最优精度阶，却在一阶临界点处只有一阶精度.然而当p=1．5时，WENO-Re3格式在一阶临界点的光滑区域也能实现最优精度阶.

注2若SC和SD分 别是包含在图1中全局模板S3的一个光滑子模板和一个间断子模板，则相应的光滑性指示子和非线性权重为

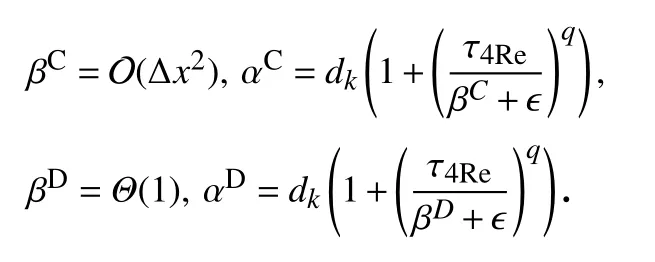
注意到τ4Re=Θ(1)，所以

那么

容易得到如下结论：当网格细化时，分配给间断模板SD的权重时，其权重ωD趋于零，因此WENO-Re3格式定义的非线性权重满足ENO性质.由于当p=1．5时的WENO-Re3格式在间断附近会产生明显的数值振荡[15]，所以在接下来的所有数值计算中取p=1， 自由参数

3 数值测试

在本节中，我们将通过一些经典数值例子来验证WENO-Re3格式的性能，并与其他WENO格式的分辨率进行比较.数值算例从简单的一维标量对流方程求解开始，然后是一维和二维Euler方程的数值求解.本文所有的格式和算例均采用局部Lax-Friedrichs通量分裂.时间推进采用三阶TVD-Runge-Kutta方法[5]：

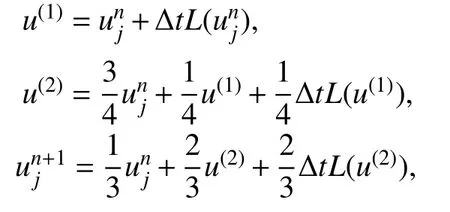
其中L(u)是对的近似.

除非另有规定，否则对于一维情形和二维情形的时间步长Δt分别为

其中σ 是CFL(Courant-Friedrichs-Lewy)条件数.在接下来的计算中取CFL数为0.6.

3.1 标量测试问题

在这一小节中，我们用具有周期边界条件的标量对流方程在不同初始值下的数值例子来验证新的WENO-Re3格式的良好性能.

例1（线性方程）考虑以下线性对流方程：

初值条件为

u(x,0)=u0(x).

首先在两组初始数据的线性方程(20)上检验WENO-Re3格式的数值收敛率：

时间步长设置为Δt=CCFL×Δx， 确保与空间精度兼容.误差的L1,L∞范 数是通过与t=2的精确解比较得出的，根据以下式子计算：

这里uexact,j表示精确值.表1和表2分别显示t=2时 初值(21a)的L1,L∞误差和收敛阶，表3和表4显示初值(21b)的结果.我们发现误差随着WENO-JS3、WENO-Z3、WENO-P3和WENO-Re3的顺序而减小，新的WENO-Re3格式能实现较好的收敛精度.相比之下，新的WENO-Re3格式的性能优于其他WENO格式.

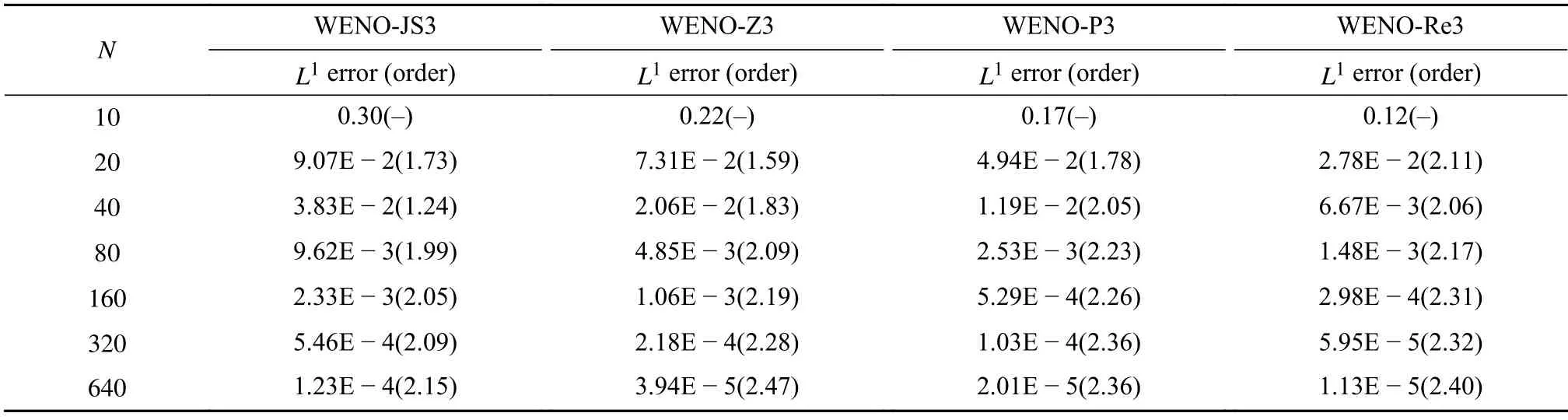
表1 线性对流方程(20)在初值(21a)下，不同格式在t =2的L1误差和收敛阶Table 1 L1 errors and convergence rates at t =2 of different schemes for linear advection eq.(20) with initial data (21a)

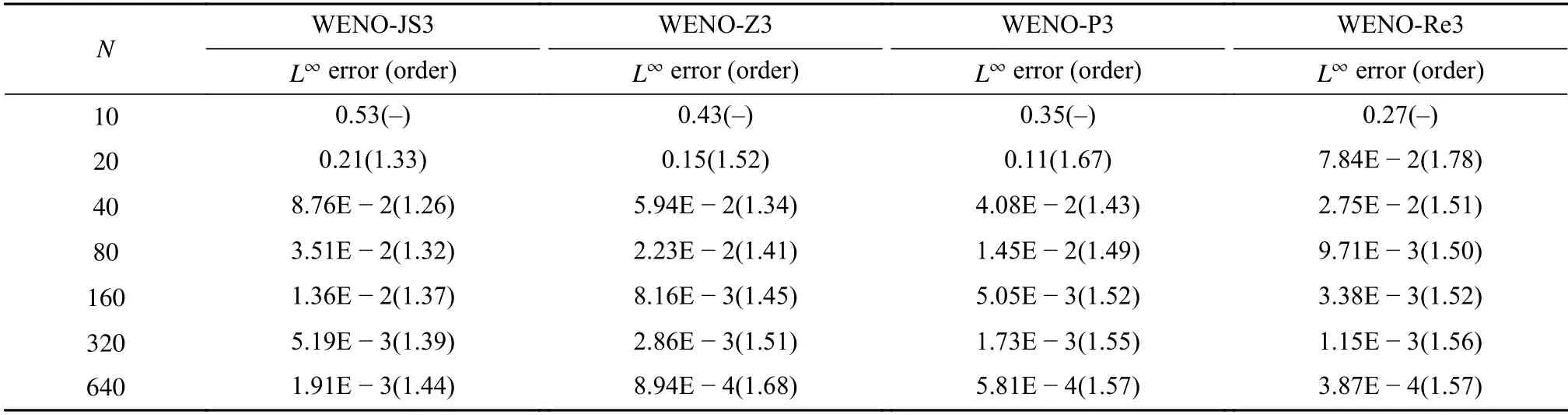
表2 线性对流方程(20)在初值(21a)下，不同格式在t =2的L∞误差和收敛阶Table 2 L∞ errors and convergence rates at t =2 of different schemes for linear advection eq.(20) with initial data (21a)

表3 线性对流方程(20)在初值(21b)下，不同格式在t =2的L1误差和收敛阶Table 3 L1 errors and convergence rates at t =2 of different schemes for linear advection eq.(20) with initial data (21b)

表4 线性对流方程(20)在初值(21b)下，不同格式在t =2的L∞误差和收敛阶Table 4 L∞ errors and convergence rates at t =2 of different schemes for linear advection eq.(20) with initial data (21b)

然后我们讨论WENO-Re3格式在长时间计算中的性能.具体来说，在式(20)上考虑如下初始条件：

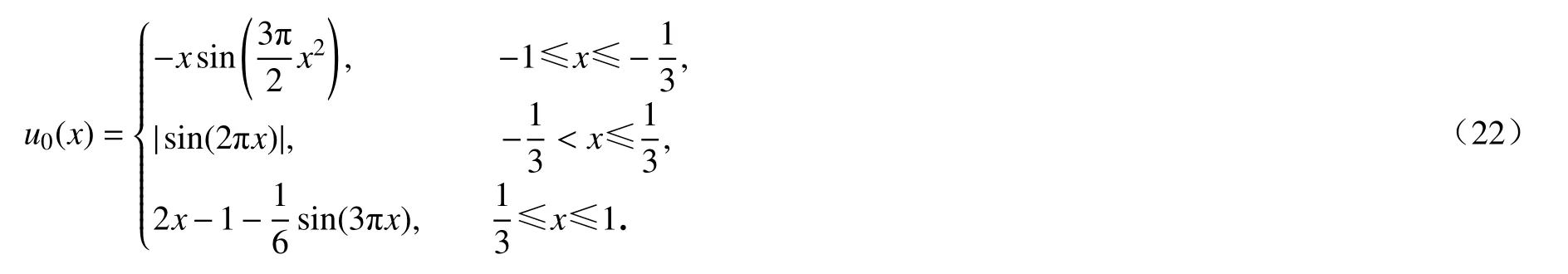
在计算域 - 1≤x≤1中 ，求解到时间为t=41， 其中 Δx=0．005.数值结果如图2所示，通过与其他WENO格式比较，可以清晰地知道在间断附近WENO-Re3的分辨率最好，并且耗散性最小.图3分别比较了WENO-Re3格式在不同参数 φ的数值结果，并且与WENO-R3格式[15]的数值结果相比较，可以清楚地知道，当参数时，WENO-Re3格式的分辨率最好，并且与WENO-R3格式[15]的分辨率大致相当.

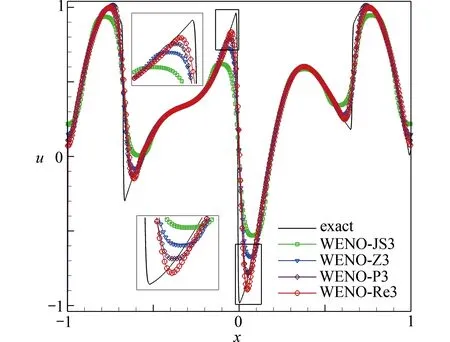
图2 线性对流方程(20)在初值(22)下，不同格式的数值解与解析解的比较，t =41，N=400Fig.2 Comparison of the analytical solution with the numerical solutions to linear advection eq.(20) with an initial value (22) at t=41, N =400

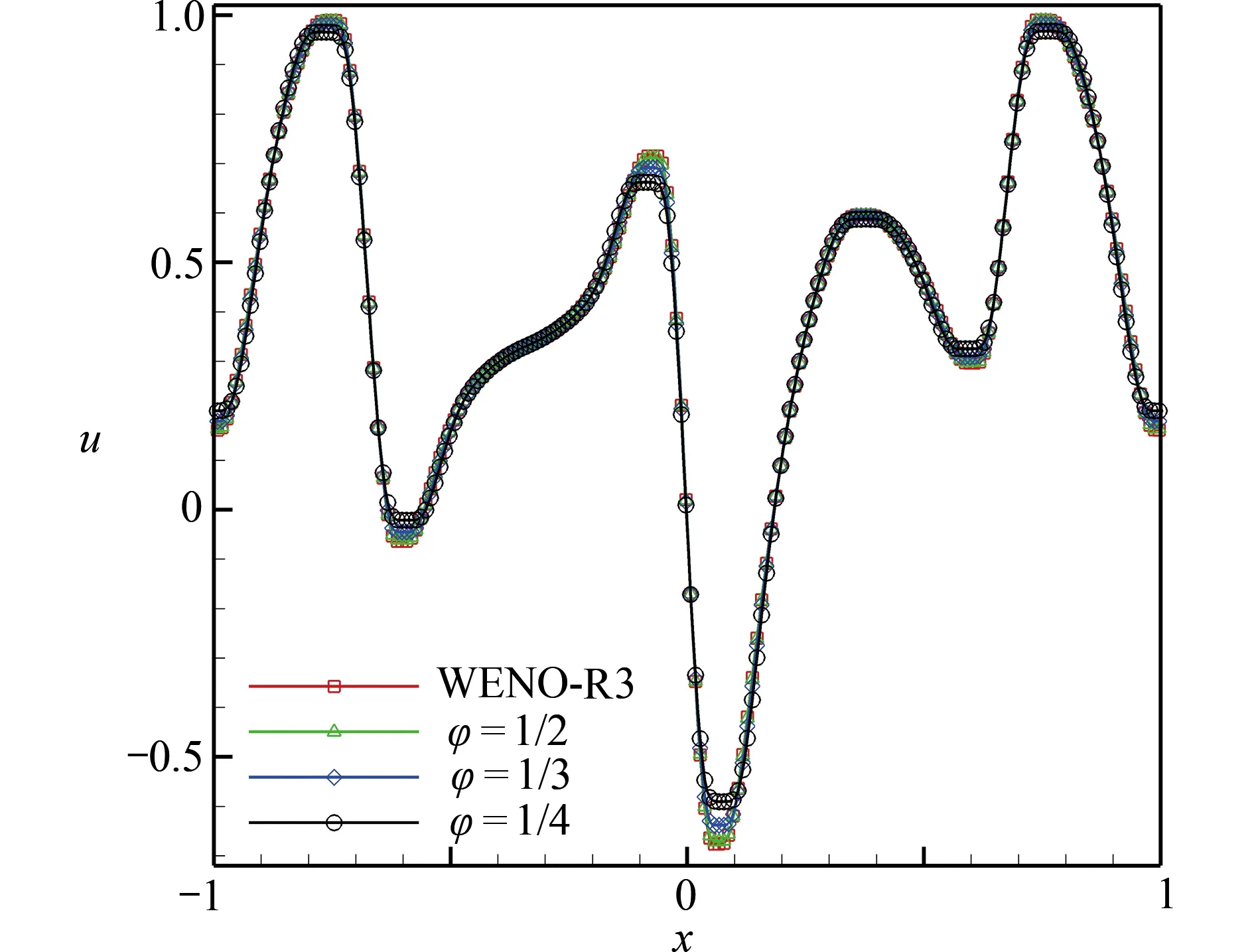
图3 线性对流方程(20)在初值(22)下，WENO-Re3格式在不同参数φ下的数值解比较，t =41，N=400Fig.3 Comparison of the numerical solutions of the WENO-Re3 scheme with different parameter φ values of linear advection eq.(20) with an initial value (22) at t =41,N=400

最后，我们求解线性对流方程(20)，初始条件包括Gauss波、方波、三角波和半椭圆波，如下所示：

其中G(x,β,z)=e-β(x-z)2，F(x,α,a)=a=0．5,z=-0．7， δ =0．005， α =10， β =ln2/(36δ2).这种情况的解包括接触间断、角点奇异和光滑区域.我们用时间步长 Δt=CCFL×Δx， 计算到最终时间为t=8.数值结果如图4和图5所示.数值结果表明，WENO-Re3格式的性能优于WENO-JS3、WENO-Z3和WENO-P3格式，并且与精确值之间的误差最小.所以基于新的光滑性指示子的三阶WENO-Re3格式比其他WENO格式具有更好的分辨率，并且WENO-Re3格式的耗散最小.

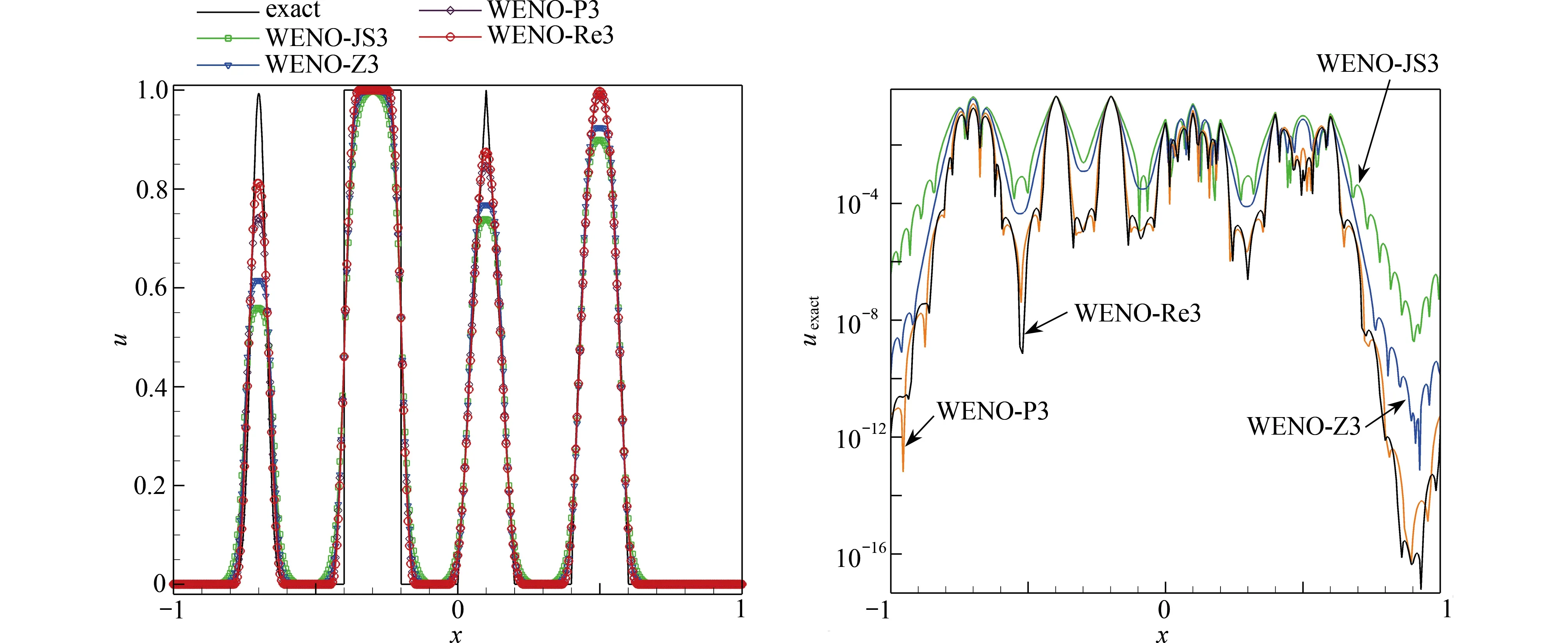
图4 线性对流方程(20)在初值(23)下，不同格式的数值解与解析解的比较，t =6，N=400Fig.4 Comparison of the analytical solution with the numerical solutions of linear advection eq.(20) with an initial value (23) at t=6, N=400

图5 线性对流方程(20)在初值(23)下，不同格式的数值解与解析解的比较，t =6，N =400（局部放大图）Fig.5 Comparison of the analytical solution with the numerical solutions to linear advection eq.(20) with initial value (23) at t=6, N=400(local encargement)

3.2 一维Euler系统

在这一节中，我们考虑一维Euler方程组：

其中

U=(ρ,ρu,E)T,F(U)=(ρu,ρu2+p,u(E+p))T.

状态方程为

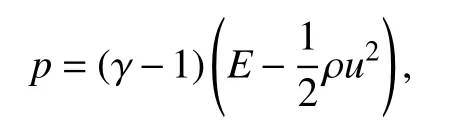
ρ,u,p和E分别是密度、速度、压强和总能，γ 是比容比.相应的Jacobi矩阵A(U)=∂F/∂U的特征值为

λ1=u-c,λ2=u,λ3=u+c,

这里c=(γp/ρ)1/2为声速.

例2 (一维Riemann问题)我们考虑具有如下形式的三个经典初值问题：

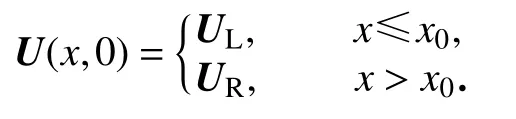
(ⅰ) Lax激波管[19-20]

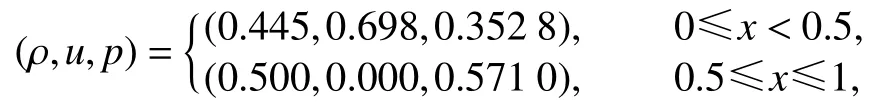
其中 γ =1．4 ， 网格尺度为 Δx=0．005， 计算时间为t=0．13.密度场的数值结果与精确的Riemann解进行了比较，如图6所示.明显地，WENO-Re3格式更高效，能更好地捕捉激波，并且耗散最小.

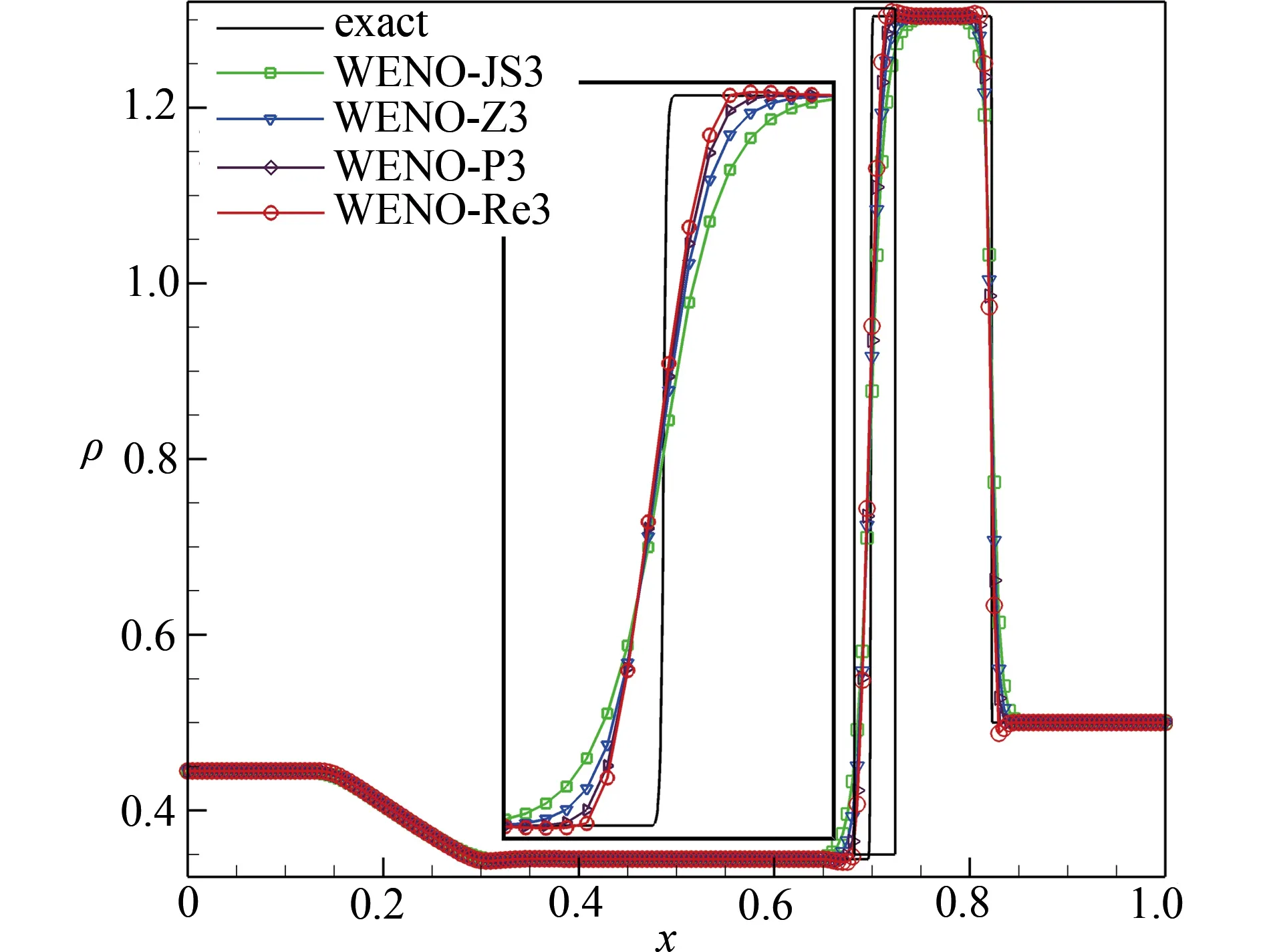
图6 Lax激波管问题[20]的数值结果，t =0．13，N=200Fig.6 Numerical results of the Lax problem[20], t =0．13,N=200

(ⅱ) 冲击波相互作用[19-20]

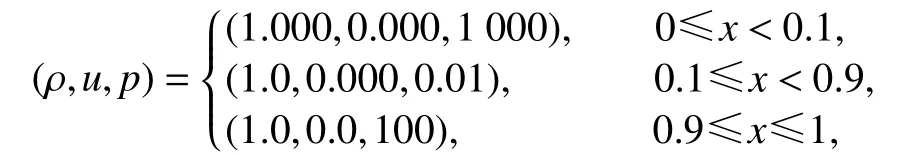
其中γ =1．4 .我们用网格尺度为Δx=0．0025 计 算到t=0．038.密度场的数值结果如图7所示.由于精确解是未知的，参考解是通过使用五阶WENO-JS格式[6]在3 201个网格点上获得的.明显可以得到，WENO-Re3格式更高效，并且在接触间断处的耗散的顺序是WENO-Re3 ＜ WENO-P3 ＜ WENO-Z3 ＜ WENO-JS3.图8分别比较了WENO-Re3在不同参数φ 的数值结果，可以清楚得到，当参数φ =1/2时，WENO-Re3格式的分辨率最好.

图7 冲击波相互作用的数值结果，t =0．038，N=400Fig.7 Numerical results of interacting blast waves, t =0．038,N=400

图8 不同参数φ 下，冲击波相互作用的数值结果，t =0．038，N=400Fig.8 Numerical results of interacting blast waves with different parameter φ values, t =0．038,N=400

(ⅲ) 一维激波等熵波作用(Titarev-Toro问题)[21]

我们计算[ -5,5]区域上的近似解，这里采用周期边界条件.初始条件为

其中γ =1．4.对于Titarev-Toro的冲击熵波测试问题，该流动包含明显的物理振荡，精确解无法得到，必须用数值方法来求解，参考解是用新的WENO-Re3格式在20 000个网格点下获得的.如图9所示，采用不同的WENO格式计算密度场的数值结果.通过与WENO-Z3和WENO-P3格式相比，WENO-Re3格式效率较好，分辨率高，并且耗散更少，特别是在捕捉高频波方面.

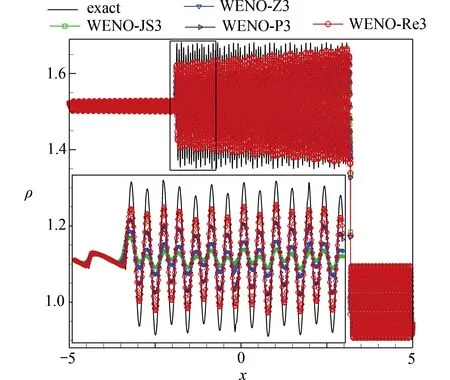
图9 激波等熵波相互作用(Titarev-Toro)[21]的密度分布，t=5，N=4001Fig.9 Density profiles of the shock entropy interaction (Titarev-Toro)[21],t=5, N=4 001

3.3 二维Euler系统

在本小节中，考虑二维可压缩Euler系统：

其中

这里 ρ，u，v，p和E分别是密度，x和y坐标方向上的速度分量，压力和总能量.另外，U是守恒变量的向量，F(U)是x方向的通量分量，G(U)是y方向的通量分量.对二维可压缩Euler方程进行了逐维求解.

例3 (二维Riemann问题)[22]计算域为[ 0,1]×[0,1]，初始条件设置为

这里边界条件为Dirichlet边界条件，比热比γ =1．4 .计算的最终时间为t=0．8.图10显示不同格式的数值结果，易得WENO-Re3格式比WENO-JS3、WENO-Z3和WENO-P3格式结构更为丰富，分辨率更高，并且耗散更小.

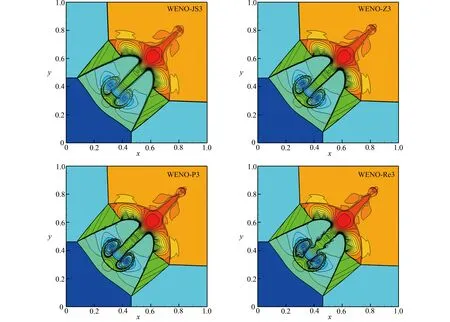
图10 不同格式关于二维Riemann问题[22]的密度等值线，Δ x=Δy=1/800，t=0．8Fig.10 Density contours of the 2D Riemann problem[22], Δx =Δy=1/800,t=0．8

例4 (双Mach反射问题)[23]激波在斜面上的二维双Mach反射描述了平面Mach激波在空气中撞击楔形物的反射现象.这种试验被广泛用于验证数值方法的性能.我们在 [ 0,4]×[0,1]上计算这个测试问题，输出在[0,3]×[0,1]上 的数值结果.起始在x=1/6处 施加一个右移Mach数为10的激波，激波前缘与x轴成 6 0°角.在沿底部边界x=0至x=1/6的区域内，为初始激波后流动赋值，其余区域采用反射边界条件.左边界为初始激波后流动赋值.对于x=4处的右侧边界都设置为零.上边界是用来描述Mach数为10的激波的精确运动.网格尺度Δx=Δy=1/480， 比热比 γ=1．4 ， 计算时间t=0．2.图11比较了WENO-Re3格式与WENO-JS3、WENO-Z3和WENO-P3格式的数值结果.可见WENO-Re3格式的分辨率比其他WENO格式要高，WENO-Re3较好地解决了Mach杆附近的不稳定性问题.

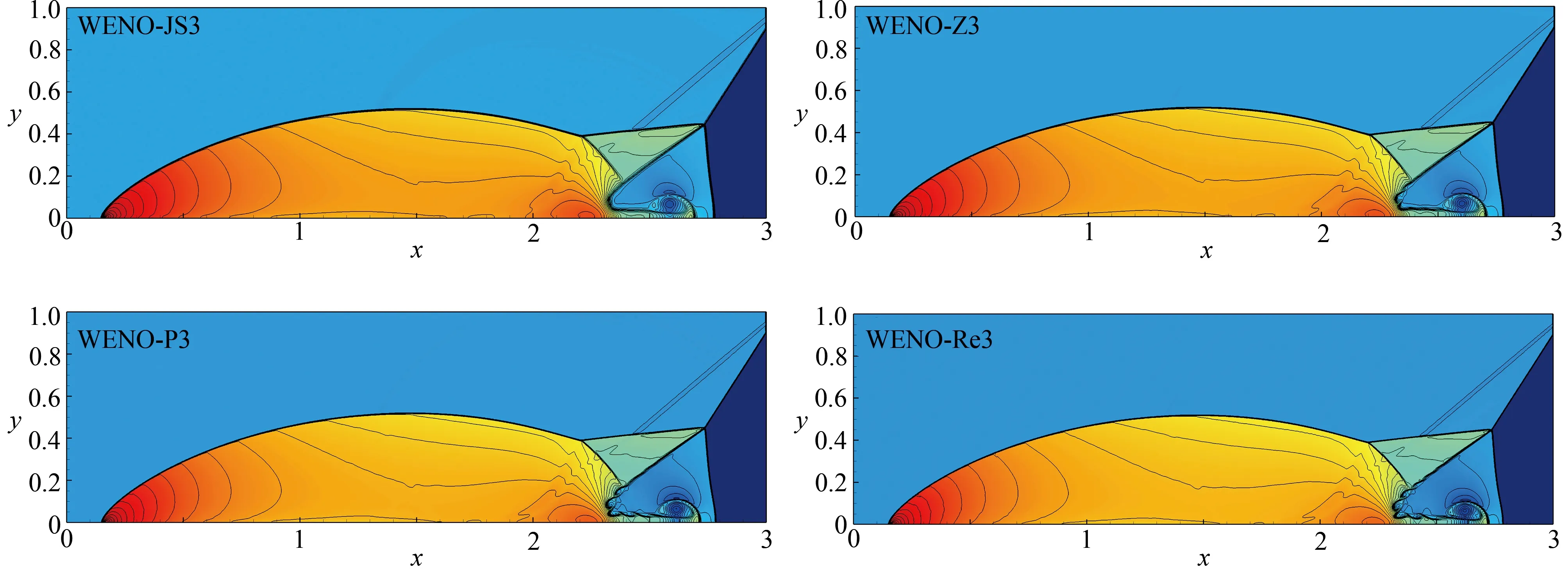
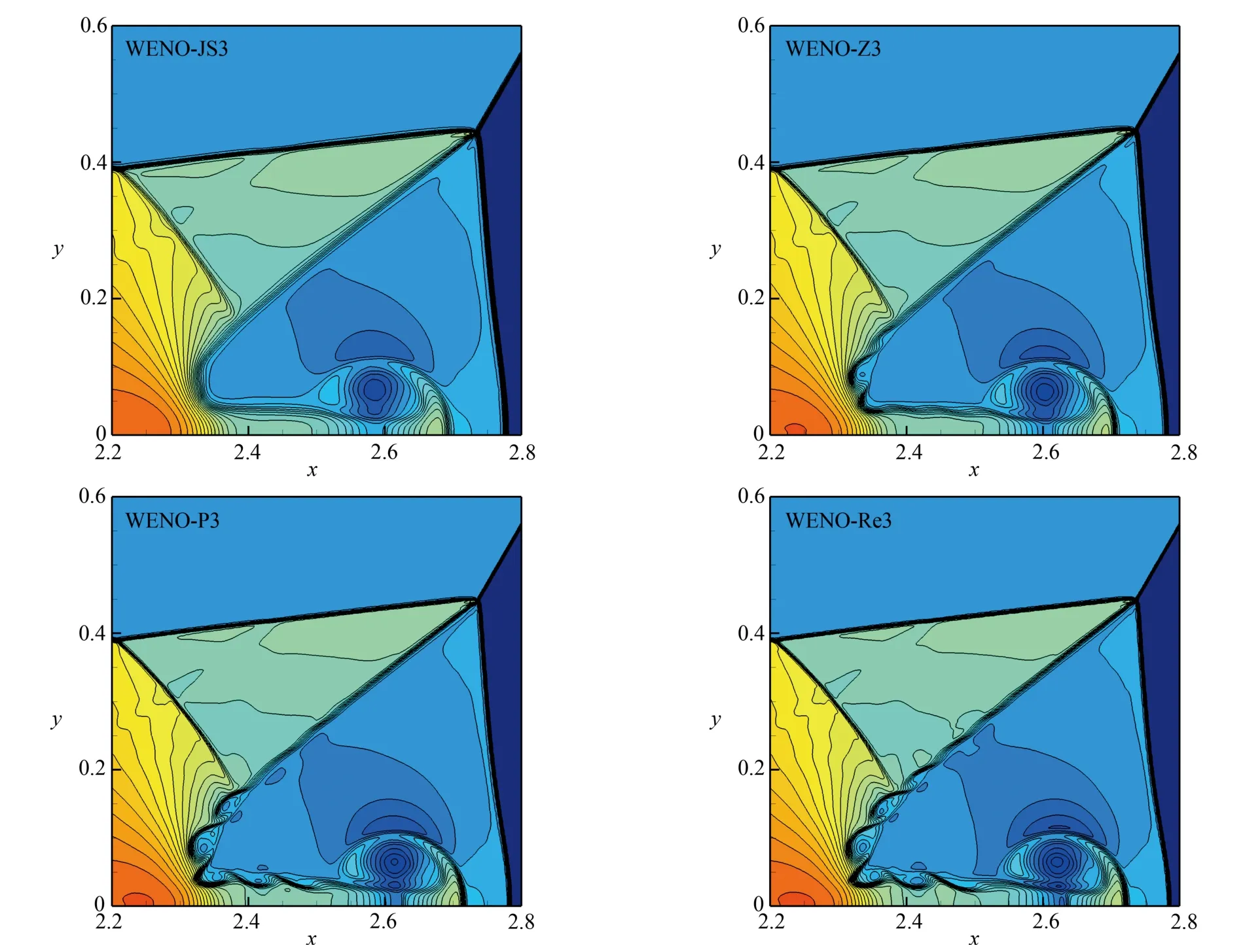
图11 双Mach反射问题在t =0．2 时 的密度等值线，网格点为1920×480Fig.11 Density contours of the double Mach reflection problem for t =0．2 on the 1 920×480 grid points

4 结 论

本文针对计算流体力学对高精度高分辨率的需求，基于降低经典的三阶WENO格式的数值耗散特性，提出了一种新的参考光滑性指示子的构造方法.其构造方法与经典的WENO-Z格式略有不同，具体实现途径是通过候选子模板的重构多项式导数的线性组合与整个全局模板上的重构多项式导数的L2范数逼近来获得的.其中引入一个介于0和1之间自由参数φ，并且通过调节该自由参数可以获得不同的参考光滑性指示子，并且获得的参考光滑性指示子的阶数比WENO-Z格式更高.本文通过一系列一维和二维数值算例验证了新格式的有效性.数值结果表明，与WENO-JS3、WENO-Z3和WENO-P3格式相比，WENO-Re3格式对精细光滑结构具有相当或更高的分辨率.

参考文献（ References ）：

［1］LIU X D, OSHER S, CHAN T.Weighted essentially non-oscillatory schemes[J].Journal of Computational Physics, 1994, 115（1）: 200-212.

［2］HARTEN A, OSHER S.Uniformly high-order accurate non-oscillatory schemes Ⅰ[J].SIAM Journal on Numerical Analysis, 1987, 24（2）: 279-309.

［3］HARTEN A, ENGQUIST B, OSHER S, et al.Uniformly high-order accurate essentially non-oscillatory schemesⅢ[J].Journal of Computational Physics, 1987, 71: 231-303.

［4］SHU C W, OSHER S.Efficient implementation of essentially non-oscillatory shock-capturing schemes[J].Journal of Computational Physics, 1988, 77（2）: 439-471.

［5］SHU C W, OSHER S.Efficient implementation of essentially non-oscillatory shock-capturing schemes Ⅱ[J].Journal of Computational Physics, 1989, 83（1）: 32-78.

［6］JIANG G S, SHU C W.Efficient implementation of weighted ENO schemes[J].Journal of Computational Physics, 1996, 126（1）: 202-228.

［7］HENRICK A K, ASLAM T D, POWERS J M.Mapped weighted-essentially-non-oscillatory schemes: achieving optimal order near critical points[J].Journal of Computational Physics, 2005, 207（2）: 542-567.

［8］BORGES R, CARMONA M, COSTA B, et al.An improved weighted essentially non-oscillatory scheme for hyperbolic conservation laws[J].Journal of Computational Physics, 2008, 227: 3191-3211.

［9］GEROLYMOS R A, SÉNÉCHAL S, VALLET I.Very-high-order WENO schemes[J].Journal of Computational Physics, 2009, 228（23）: 8481-8524.

［10］WANG Y H, DU Y L, ZHAO K L, et al.Modified stencil approximations for fifth-order weighted essentially nonoscillatory schemes[J].Journal of Scientific Computing, 2019, 81（6）: 898-922.

［11］FU L, HU X Y, ADAMS N A.A new class of adaptive high-order targeted ENO schemes for hyperbolic conservation laws[J].Journal of Computational Physics, 2018, 374: 724-751.

［12］WU X S, ZHAO Y X.A high-resolution hybrid scheme for hyperbolic conservation laws[J].International Journal for Numerical Methods in Fluids, 2015, 78（3）: 162-187.

［13］WU X S, LIANG J H, ZHAO Y X.A new smoothness indicator for third-order WENO scheme[J].International Journal for Numerical Methods in Fluids, 2016, 81（7）: 451-459.

［14］XU W Z, WU W G.An improved third-order WENO-Z scheme[J].Journal of Scientific Computing, 2018, 75:1808-1841.

［15］WANG Y H, DU Y L, ZHAO K L, et al.A low-dissipation third-order weighted essentially nonoscillatory scheme with a new reference smoothness indicator[J].International Journal for Numerical Methods in Fluid, 2020,92（9）: 1212-1234.

［16］王亚辉.求解双曲守恒律方程的三阶修正模板WENO格式[J].应用数学和力学, 2022, 43（2）: 224-236.（WANG Yahui.A 3rd-order modified stencil WENO scheme for solution of hyperbolic conservation law equations[J].Applied Mathematics and Mechanics, 2022, 43（2）: 224-236.（in Chinese））

［17］徐维铮, 孔祥韶, 吴卫国.基于映射函数的三阶 WENO 改进格式及其应用[J].应用数学和力学, 2017, 38（10）: 1120-1135.（XU Weizheng, KONG Xiangshao, WU Weiguo.An improved 3rd-order WENO scheme based on mapping functions and its application[J].Applied Mathematics and Mechanics, 2017, 38（10）: 1120-1135.（in Chinese））

［18］徐维铮, 吴卫国.三阶WENO-Z格式精度分析及其改进格式[J].应用数学和力学, 2018, 39（8）: 946-960.（XU Weizheng, WU Weiguo.Precision analysis of the 3rd-order WENO-Z scheme and its improved scheme[J].Applied Mathematics and Mechanics, 2018, 39（8）: 946-960.（in Chinese））

［19］LAX P D.Weak solutions of nonlinear hyperbolic equations and their numerical computation[J].Communications on Pure and Applied Mathematics, 1954, 7（1）: 159-193.

［20］SOD G A.A survey of several finite difference methods for systems of nonlinear hyperbolic conservation laws[J].Journal of Computational Physics, 1978, 27（1）: 1-31.

［21］TITAREV V A, TORO E F.Finite-volume WENO schemes for three-dimensional conservation laws[J].Journal of Computational Physics, 2004, 201（1）: 238-260.

［22］SCHULZ-RINNE C W, COLLINS J P, GLAZ H M.Numerical solution of the Riemann problem for two-dimensional gas dynamics[J].SIAM Journal on Scientific Computing, 1993, 14（6）: 1394-1414.

［23］WOODWAED P, COLELLA P.The numerical simulation of two-dimensional fluid flow with strong shocks[J].Journal of Computational Physics, 1984, 54（1）: 447-465.