气固两相弯管湍流场中圆柱状颗粒取向和沉积特性的研究*
2022-07-20石瑞芳林建忠
李 亮, 石瑞芳, 林建忠
(1.浙江大学 航空航天学院 流体工程研究所,杭州 310027;2.广东盈峰智能环卫科技有限公司,广东 佛山 528322)
引 言
气固两相流中,管道气力输送颗粒具有占地面积小、无污染、设置灵活、输送距离长等优点,因而广泛应用于机械制造、冶金、发电、材料工程、制药和食品生产等各个行业.气力输送过程中,颗粒在管道中的沉积会导致管道的堵塞,降低系统的效率甚至影响安全生产.可见,研究气力输送过程中颗粒在管道中的输运与沉积对工程应用具有重要意义.颗粒在管道壁面上的沉积与热泳力[1]、颗粒惯性力、重力[2]、Brown和湍流扩散[3]有关,是个复杂的过程.在以往的研究中,已有一些内容涉及颗粒在直管中的输运和沉积[4-8].然而,在实际应用中弯管的情形是很普遍的,弯管中的流体在离心力的作用下产生二次流,将颗粒输送至壁面附近的区域;颗粒本身也会在离心力作用下甩向弯道的外壁,这将导致颗粒在壁面沉积率的增加.因此,有必要研究颗粒流经弯管湍流场时的沉积特性.
目前,已有一些颗粒流经弯管湍流场的研究结果.Pui等[9]实验研究了Reynolds数100<Re<10 000、颗粒直径0.1 µm≤dp≤10 µm的情况下,颗粒流经弯管时的通过率,发现通过率既不依赖于弯管的曲率也不依赖于Re.Balásházy等[10]研究了颗粒的惯性碰撞和重力沉降,发现在吸入的情况下管道横截面中的二次流对沉积率没有显著影响.Lee和Gieseke[11]指出,对于颗粒直径0.035 µm≤dp≤1.3 µm、Reynolds数1 800<Re<15 600的情形而言,当颗粒的惯性沉降和Brown扩散同时起作用时,仅用以往的理论无法令人满意地预测颗粒的最小沉积率.Sato等[12]发现颗粒的沉积率随Stk和De的增加而提高,随弯道曲率的减小而降低.Wang等[13]指出,当Re较低时,直径为5 nm≤dp≤15 nm颗粒扩散损失的增加对弯管的取向比较敏感.Yook和Pui[14]发现在Dean数21≤De≤1 779的情况下,直径为3 nm≤dp≤50 nm颗粒的通过率随着粒径和De的增加而增加,而当De>200时, 曲率对通过率的影响可以忽略.Lin等[15]说明当Schmidt数Sc较小时,颗粒在管道中的分布主要由轴向速度决定,而当Sc远大于1的数量级时,二次流将主导颗粒的分布,颗粒的沉积区域随着De的增加而变得均匀.Wilson等[16]指出,在一定的Stk范围内,Re的增加并不会显著改变颗粒沉积率的变化趋势,而在0.1≤Stk≤0.4范围内,颗粒沉积率随Re的增加而显著增加;当Stk=0.15时,Re从10 250增加到30 750会导致沉积率从0.14增加到0.36.Ghaffarpasand等[17]发现,当1 426≤De≤2 885时,直径为3 nm≤dp≤17 nm颗粒的通过率随着曲率的增加而增加,而对Re的变化却不敏感.Lin等[18]指出,对直径为8 nm≤dp≤550 nm的颗粒,De对通过率的影响依赖于Sc;存在一个临界De,超过该临界De时,通过率由增加变为减少,而这个临界值依赖于Sc;De越大,颗粒的通过率越高.
以上所述的颗粒都是圆球形状,而在实际应用中,非圆球颗粒例如圆柱状或椭球状颗粒还是很常见的.非圆球颗粒在气流中的输运比圆球的情形复杂,因为颗粒的旋转及其取向与颗粒的平动存在耦合,而迄今为止,鲜有对非圆球颗粒流经弯管湍流场时颗粒取向和沉积特性的研究.圆柱状颗粒是非圆球颗粒中最典型的一类,因此,本文首先数值求解流体的平均运动、湍动能、耗散率和脉动速度方程,然后数值求解圆柱状颗粒的运动和取向方程,得到不同参数下颗粒取向沿流向不同截面和出口处的分布以及颗粒流经弯管时的沉积率.
1 圆柱状颗粒基本方程
圆柱状颗粒流经一个弯管的流场如图1所示,图中S是位于xOy平面的弯管的中线,r和θ是定义在横截面上的极坐标,u,v和w分别是r, θ和S方向的速度分量,a和R分别是弯管内径和曲率.

图1 弯管流场和坐标系Fig.1 The flow field of the curved tube and the coordinate system
在固定坐标系Oxyz上的圆柱状颗粒的取向可以由图2中的 φ和ψ确定,其中坐标系O123固定在颗粒上,方向3沿着颗粒的长轴,方向1是颗粒长轴在xOy平面上的投影方向,方向2是垂直于1O3平面的方向,φ是颗粒在xOy平面上的投影与x轴之间的夹角.本文假设颗粒为刚性圆柱状颗粒,绕颗粒的流动是Stokes流,颗粒对流体的影响忽略不计.
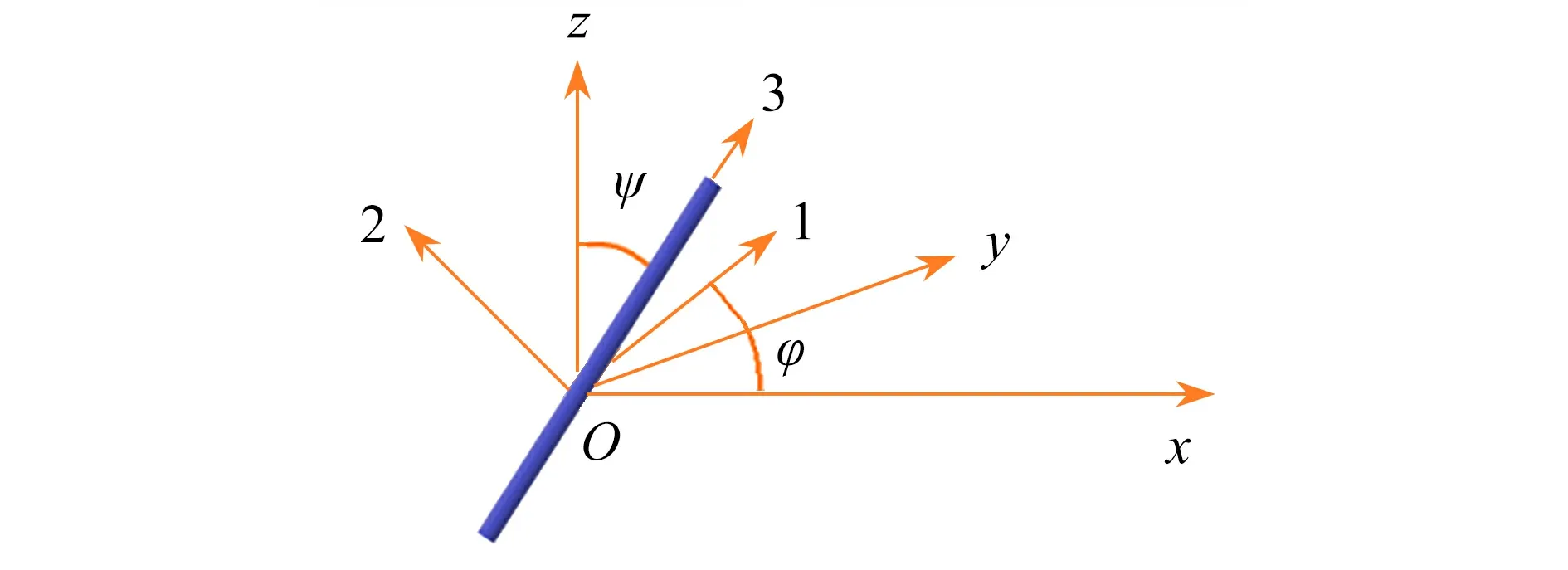
图2 两个坐标系
1.1 圆柱状颗粒数值计算模型
圆柱状颗粒在流体中运动的受力和速度模型采用Batchelor提出的细长体理论[19],即由圆柱状颗粒引起的流场扰动速度与由Stokeslet线分布引起的扰动速度相同,Stokeslet是Stokes流中的奇点施加到流体上的力,基于对Stokes方程的求解,可以得到该力以及由该力诱导的流场扰动速度.在细长体理论中,圆柱状颗粒被分为若干段,每一段施加到流体上的力用一个Stokeslet点力表示,沿着圆柱状颗粒主轴长度积分,便可以得到圆柱状颗粒诱导的流场扰动速度[20]:

式中u是流体的瞬时速度;xc是颗粒质心的坐标;vp和ω分别是颗粒的速度和角速度;l和p分别是颗粒长度和取向的单位矢量;s是沿颗粒主轴的无量纲坐标,-1≤s≤1;β是颗粒的长径比;b(s)是在s处颗粒横截面的形状因子(对于圆柱状颗粒b(s)=1);δ是单位矩阵;f(s)是流体施加在颗粒上的力.方程(1)左边的项是颗粒和流体在流场某一点的速度差.首先根据Gauss积分点将圆柱状颗粒划分为M段,然后在每一段上把f(s)变换成f(si),最后,将方程(1)右边积分转换为一系列f(si)的线性求和,这样就可以将方程(1)转换为3M个线性方程组:

式中lm是圆柱状颗粒第m段的长度,f(si)由求解方程(2)得到.通过对以下方程数值积分,便可获得流体施加在圆柱状颗粒上的合力F与合力矩L:

1.2 圆柱状颗粒运动方程
圆柱状颗粒在流体拖曳力、离心力和随机力作用下的运动方程如下所示[21],其中随机力基于Stokes-Einstein的色散理论:

式中m是颗粒质量;Rb是均值和方差为零的Gauss随机分布的随机向量;dpe是圆柱状颗粒的体积当量直径;kB是Boltzmann常数;T是温度;µ是流体的动力黏度;Δt是随机力作用的时间间隔;Ji是颗粒的惯性矩;Li是力矩分量;ωi是颗粒角速度分量;下标1、2和3表示坐标系O123中的3个分量.
以下方程用于将方程(5)中的力矩从坐标系O123转换为坐标系OrθS:

1.3 圆柱状颗粒的取向分布函数
圆柱状颗粒的取向分布函数Ψ由Fokker-Planck方程控制[22-23]:

式中ω是颗粒的角速度;D是旋转扩散系数;Rr是颗粒旋转的阻力系数[24];l是颗粒长度;ρ和ν分别是流体的密度和运动黏性系数.方程(7)右边的第一项表示流体作用力的影响,第二项是随机力影响.圆柱状颗粒的取向由分布函数Ψ描述,它表示颗粒取向位于某一角度范围内的概率.
1.4 颗粒碰撞模型
间步长为Δt= (u-vi)/, 这里u-是颗粒和流体的速度差颗粒在时间步长i的加速度.在下一时间步
当颗粒流过弯管时,颗粒会发生相互碰撞且有可能和管壁发生碰撞,这种碰撞会影响颗粒的平移和旋转速度从而影响颗粒的分布和通过率.如图3所示,假设两个圆柱状颗粒的碰撞为瞬时、非完全弹性碰撞,图中两颗粒接触点及其法线方向n由两颗粒的相对位置决定.本文圆柱状颗粒基于细长体理论建模,故一个颗粒被分成M段,每一段被视为一个单元,每个单元参与颗粒间碰撞的判断.在对方程(4)、(5)的积分过程中,变时i+ 1,如果颗粒1的i段质心与颗粒2的j段质心之间的距离在dp-dp/10到dp+dp/10的范围之内,则认为两个颗粒发生碰撞.如果距离小于dp-dp/10,则原始时间步长减少一半并重新计算.假设碰撞点O位于颗粒1的i段质心和颗粒2的j段质心连线的中点,l1和l2分别是从两个颗粒质心O1和O2到接触点O的矢量,从而定义法向矢量n=l1+l2.碰撞时两个颗粒沿法线方向获得一个冲量,碰撞后两个颗粒的平动速度和角速度取决于该冲量:

图3 两颗粒碰撞示意图Fig.3 Schematic of the collision between 2 particles

式中m和vp分别是颗粒质量和速度;下标1、2表示颗粒1和颗粒2;上标“′”表示碰撞后.基于碰撞定律得

式中e是恢复系数;vp1o和vp2o是碰撞前接触点处两个颗粒沿法向的速度分量.作用在两个颗粒上的力矩分别是In×l1和-In×l2,于是颗粒的旋转方程为

那么冲量I可以写成

当颗粒1与壁面碰撞时,颗粒2可视为壁面,此时m2和vp2分别视为无穷大和零.
2 流场基本方程
要解方程(2) ~ (8),首先要求解流场得到流场的瞬时速度u,该速度由平均速度U和脉动速度u′组成.
2.1 平均运动方程
假设流动为不可压且充分发展的湍流,连续性方程和Reynolds平均运动方程为

式中Ui是平均速度,由3个分量Ur,Uθ和US构成;P是平均压力;ρ和ν分别是流体密度和运动黏性系数;是Reynolds应力.定义平均轴向速度为

式中B=-∂P/∂S;µ是流体动力黏性系数;a是管道半径.定义无量纲参数如式(16)所示,用其对方程(14)无量纲化得方程(17):

2.2 Reynolds应力方程
方程(14)中的Reynolds应力由以下方程描述:
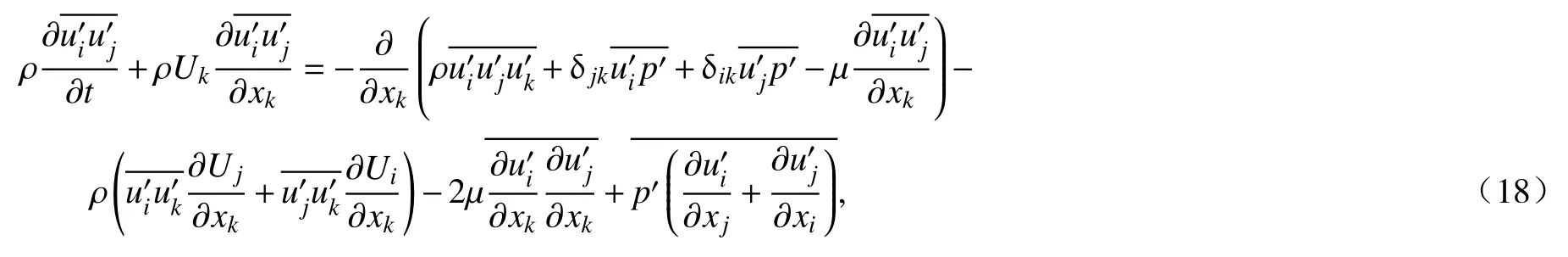
式中p′是脉动压力.方程(18)右边第一项的湍流扩散项可以模化为[25]

以上方程中包含的k和ε的修正方程为
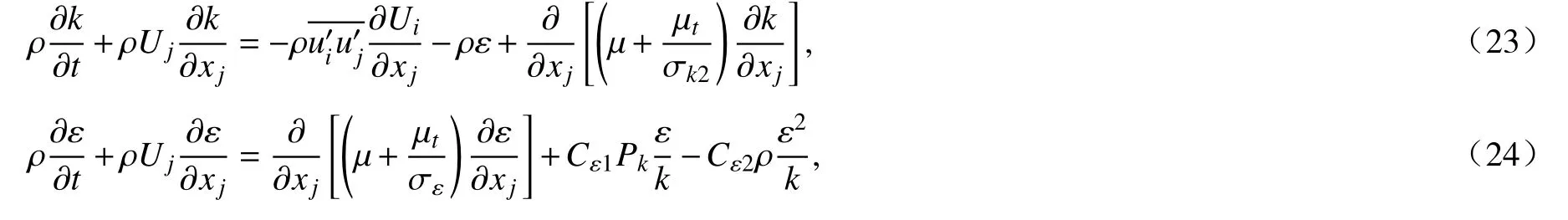
式中Cε1=1.44,Cε2=1.92, σk2=1.0, σε=1.3.
2.3 流体脉动速度
湍流扩散由流体脉动速度u′体现,一个湍流场可以用Fourier模式、单点速度关联表达式和标量能谱表示.均匀各向同性湍流中的速度场可以模拟不同模态之间的动力相互作用以及涡度场对流的运动学过程.Kolmogorov局部各向同性湍流的假设说明,小尺度湍流运动在统计上是各向同性的,流体的脉动速度u′与小尺度湍流运动有关.因此,可以选择均匀各向同性湍流模型来得到流体的脉动速度.为了得到流体的脉动速度u′,基于动力学模拟扫掠模型[28-29],用Fourier级数来表示u′:

式中ξ(n)和ζ(n)是满足平均值为零、标准差为的Gauss分布的随机矢量,其中N是常数,本文取N=100;频率ω(n)是标准差为u′的均方根的Gauss随机数;波数矢量k(n)是单位球面上各向同性的随机矢量.ω(n)和半径k(n)的分布函数由下式确定:

式中E(k)是 Karman-Pao湍流能谱;D(τ)是二阶关联函数.那么ω(n)和k(n)服从Cauchy分布:


3 数值模拟
3.1 求解步骤
1)求解方程(13) ~ (24)得到Ui,k和ε;
2) 求解方程(25) ~ (28)得到u′;
3)对颗粒位置、取向、速度和角速度进行初始化;
4)由方程(2)、(3)计算F和L;
5)由方程(6)将L从坐标系Oxyz变换到坐标系O123;
6)由方程(4)、(5)和方程(7)、(8)计算下一时间步的颗粒位置和取向;
7)返回步骤4),直到颗粒流出管道或沉积在管壁上;
8)计算颗粒的沉积率Dep=(Nin-Nout)/Nin,这里Nout和Nin分别是管道出口和入口的颗粒数.
3.2 数值模拟方法和相关参数
用有限体积法求解方程(7)、(8)和方程(13)、(14),采用SIMPLE格式处理速度-压力耦合项,对流项用幂律格式离散,该格式是一维对流-扩散型方程精确解的分段近似,能给出物理真实解.模拟中采用交错网格,压力、轴向速度US位于控制体中心,而横截面上的速度分量Ur和Uθ位于控制体的边界.壁面采用无滑移边界条件,标准壁面函数用于近壁区域的计算,最靠近壁面单元的中心与壁面的距离为y+=30.用显式Euler公式积分方程(4)、(5),得到下一时间步颗粒的速度和角速度.数值模拟中的相关参数为ρ=1.205 kg/m3,µ=1.808 ×10-5Pa·s,T=293 K,kB=1.38 × 10-23J/K,e=0.37.20 000个圆柱状颗粒初始均匀地分布于管道的入口,其取向沿各方向也是均匀分布,对中心线长度Lb=πR/2的90°弯曲管进行计算.
文中的Re,De和曲率的定义如式(16)所示,Stk定义为颗粒响应时间与流动特征时间之比:

式中ρp是颗粒密度;uτ是壁摩擦速度.
3.3 网格独立性及数值模拟方法验证
网格单元的数量为128(r) × 128(θ) × 256(S),在θ和S方向采用均匀网格、沿r方向的网格越靠近壁面越密.将r和θ方向的网格点从112变化为144、S方向网格点从240变化为272,进行网格的独立性验证,把每个物理量的所有归一化剩余误差小于10-4作为计算收敛的准则.
为了验证数值模型和方法,将本文数值模拟得到的管道出口处流场截面上沿水平中线上的平均轴向速度分布和轴向脉动速度的均方根与实验结果[31]进行比较,结果如图4所示,可见数值模拟结果与实验结果基本相符.
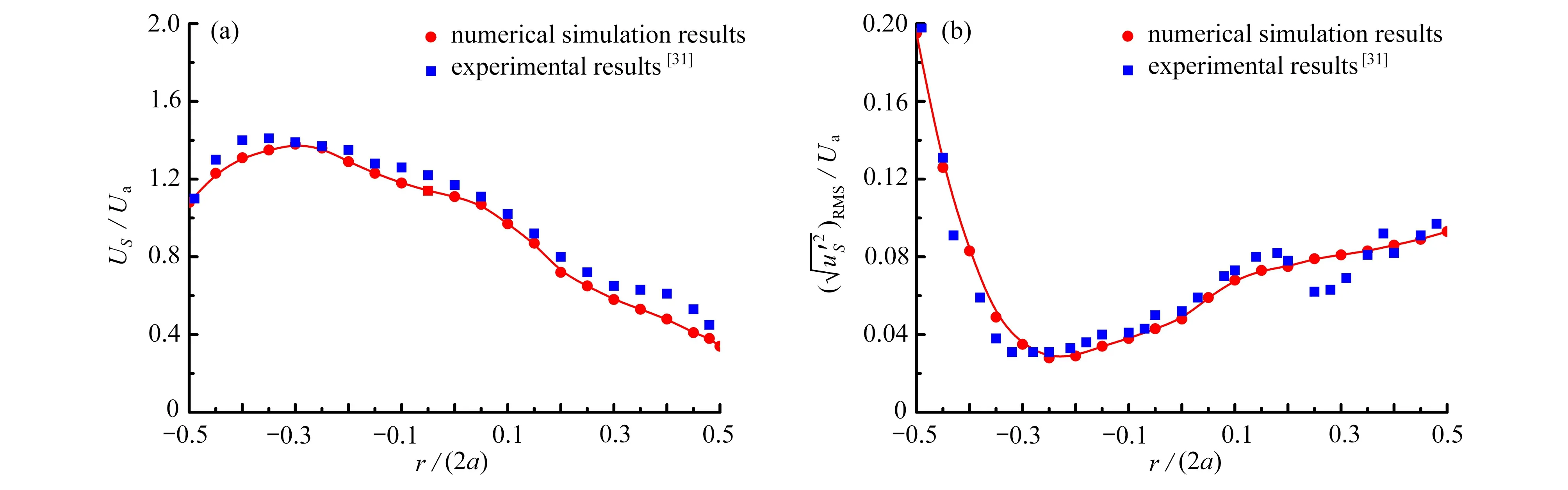
图4 平均轴向速度和轴向脉动速度均方根的分布(Re=10 500, De=2 460):(a)平均轴向速度;(b)轴向脉动速度均方根Fig.4 Distributions of the mean axial velocity and the RMS value of the fluctuating axial velocity (Re=10 500, De=2 460): (a) the mean axial velocity;(b) the RMS value of the fluctuating axial velocity
4 结果与讨论
4.1 颗粒取向在不同轴向位置的分布
不同轴向位置处横截面上颗粒平均取向分布如图5所示,图中横坐标 ϕ是颗粒的主轴与流场当地流线的夹角,通过对固定轴向位置横截面上所有颗粒的取向角进行平均得到,纵坐标是概率.流场中的速度矢量用速度的三个分量值计算得到,颗粒的取向矢量由求解取向分布函数方程(7)得到.由图可见,颗粒的平均取向从入口的各向同性分布沿流动方向变为非各向同性分布,颗粒的取向逐渐趋向于流动方向.由方程(5) ~ (8)可知,颗粒的取向由流体施加在颗粒上的力矩和Brown扩散所控制,后者使颗粒取向分布变得更加各向同性,那么颗粒取向趋向于流动方向是由前者的力矩所造成,力矩一方面使颗粒绕涡量轴旋转,另一方面使颗粒旋转后的取向趋向于流动方向.

图5 横截面上颗粒平均取向分布(Re=30 000, Stk = 1, De=2 200,β=8)Fig.5 Distributions of mean orientations of particles on the cross section (Re =30 000, Stk =1, De=2 200,β=8)
4.2 颗粒取向在出口截面处的分布
出口处横截面上Stk和De对颗粒平均取向分布的影响如图6、7所示.由图6可见,随着Stk的增加,颗粒取向趋向于流动方向的现象更明显.因为如方程(7)、(8)所示,颗粒的取向由流体阻力和Brown随机力控制,Brown随机力使颗粒的取向趋向均匀分布,削弱其占优取向的趋势,而对于Stk较大的颗粒而言,Brown随机力的作用相对较弱.

图6 不同Stk时,颗粒平均取向分布(Re=30 000, De=2 200, β=8)Fig.6 Distributions of particle orientations for different Stk values(Re =30 000, De =2 200, β=8)
从图7可以看出,随着De的增加,颗粒取向趋向于流动方向的现象变得不明显,因为De与曲率κ成正比(见式(16)),而弯管内二次流的强度与曲率κ成正比,大的De意味着大的二次流强度,二次流施加在颗粒上的力起着阻止颗粒取向趋向于流动方向的作用.

图7 不同De时,颗粒平均取向分布(Re =30 000, Stk=1, β=8)Fig.7 Distributions of particle orientations for different De values(Re=30 000, Stk=1, β=8)
出口横截面上Re和颗粒长径比β对颗粒平均取向分布的影响如图8、9所示.由图8可见,随着Re的增大,颗粒取向趋向于流动方向的现象减弱.其原因有两个方面,方程(2)、(4)表明,流体作用在颗粒上的力矩是由颗粒速度和流体瞬时速度之差产生的,而流体瞬时速度由平均速度U和脉动速度u′组成,平均速度及其所诱导的剪切率使颗粒旋转并导致取向趋向于流动方向,而随机的脉动速度导致颗粒旋转并使其取向趋向于各向同性分布.Reynolds数是表征湍流的重要参数,Reynolds数越大,最小涡的尺度越小,不同尺度的旋涡所包含的能谱分布越广,脉动速度的影响越大,于是颗粒取向趋向于流动方向的现象越不明显.另一方面,当Re较大时,流动中会出现较强的二次流,这也会阻碍颗粒的取向趋向于流动方向.

图8 不同Re时,颗粒取向分布(De=2 200, Stk=1, β=8)Fig.8 Distributions of particle orientations for different Re values(De=2 200, Stk=1, β=8)
在图9中,随着颗粒长径比β的增加,颗粒取向更趋向于流动方向.流体作用在颗粒上的力矩与涡的尺度有关,即大尺度和小尺度的涡分别对应于平均速度U和脉动速度u′,长径比小的颗粒受脉动速度u′的影响较大,于是颗粒取向趋向于流动方向的现象不明显.由图还可见,在大长径比的情况下,β对颗粒平均取向分布的影响较小,这与Krushkal和Gallily[32]得出的结论一致,该结论认为当颗粒长径比大于5时,颗粒的取向分布对长径比的变化不敏感.
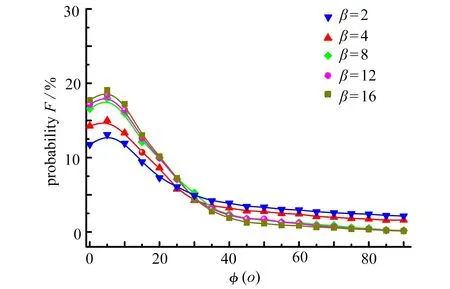
图9 不同β时,颗粒取向分布(Re=30 000, De =2 200, Stk=1)Fig.9 Distributions of particle orientations for different β values(Re=30 000, De =2 200, Stk=1)
4.3 Stk和颗粒长径比对颗粒沉积率的影响
本文采用的细长体理论将圆柱状颗粒分成M段,每一段都被视为采样单元作为与壁面碰撞的判断依据,如果某一段的质心与壁面之间的距离小于dp/2,则确定颗粒碰到壁面.当撞击壁面的颗粒碰撞速度较低时,颗粒将因不足以逃脱壁面吸引力而沉积在壁面上.模拟中当颗粒碰撞后垂直于壁面的速度分量小于或等于零时,就认为颗粒沉积在壁面上.如方程(4)、(5)所示,颗粒的沉积数量取决于颗粒轨迹,而该轨迹与作用在颗粒上的力、力矩和颗粒长径比有关.二次流会增强颗粒向壁面的传输从而提高颗粒的沉积率.
为了验证数值模拟颗粒沉积率结果的可靠性,本文计算了当颗粒长径比β=1时在不同Stk情况下颗粒流经弯管的通过率Pe=Nout/Nin,这里Nout和Nin是管道出口和入口的颗粒数,通过率Pe和沉积率Dep的关系为Dep=1 -Pe.图10是数值模拟结果与实验结果[17]的比较,可见两者吻合较好.

图10 不同Stk下的颗粒通过率(De=1 862, Re=10 500, β=1)Fig.10 The pass ratio of particles at different Stk values (De=1 862,Re=10 500, β=1)
图11是不同颗粒长径比(β)情况下沉积率与Stk的关系,可见沉积率并非Stk的单调函数,当Stk较小时,随机力对颗粒的影响大于惯性力的影响,近壁区的颗粒较容易被随机力驱使到达壁面,导致较大的沉积率.随着Stk的增加,随机力的作用逐渐减弱,近壁区中的颗粒到达壁面的数量减少,沉积率也逐渐降低,这与以往的圆球颗粒的通过率随着颗粒直径的增加而增加的结论[14]一致,因为Stk与颗粒直径成正比.当Stk进一步增加到Stk≈7时,惯性力的作用大于随机力的作用,较多的颗粒朝壁面附近运动并到达壁面,导致颗粒的沉积率有所回升,这与圆球情形的结论[12]是吻合的.
由图11还可知,颗粒沉积率随颗粒长径比β的增加而增加,其原因可分析如下:长径比越大的颗粒承受的惯性离心力越大,因而越容易在靠近弯管外侧壁面的区域聚集,这为颗粒的沉积提供了条件.另一方面,具有较大长径比颗粒的旋转导致颗粒更容易到达并沉积在壁面上.上述结论与直管情况下的结论一致,即刚性纤维的沉积率比圆球颗粒的沉积率高[33].

图11 不同颗粒长径比时沉积率与Stk的关系(Re=30 000, De=2 200)Fig.11 The relationship between the deposition rate and Stk at different particle aspect ratios (Re=30 000, De=2 200)
4.4 Re和De对颗粒沉积率的影响
图12和13分别给出了颗粒沉积率与Re和De的关系,可见沉积率随着Re和De的增加而增加,这与圆球情形[33]相同.Re和De较大的情况下,颗粒更容易被较强的二次流带向壁面,导致颗粒碰撞壁面从而沉积在壁面的可能性增大,这与式(16)中De与Re成正比的定义是吻合的.比较图12和13可知,在本文计算的Re和De范围内,Re对颗粒沉积率的影响比De的影响明显,在式(16)中,De与Re的关系相差一个曲率的因子κ,而κ小于1,所以这一结论也与式(16)中的定义吻合.

图12 不同Re下沉积率与Stk的关系(De=2 200, β=8)Fig.12 The relationship between the deposition rate and Stk at different Re values (De =2 200, β=8)

图13 不同De下沉积率与Stk的关系(Re =30 000, β=8)Fig.13 The relationship between the deposition rate and Stk at different De values (Re =30 000, β=8)
5 结 论
本文对圆柱状颗粒流经弯管湍流场时的取向与沉积特性进行了研究,首先求解流体平均运动、湍动能、耗散率和脉动速度方程,然后求解颗粒运动方程和取向的Fokker-Planck方程,得到颗粒取向在不同轴向位置和出口截面处的分布以及颗粒流经弯管时的沉积率,一些数值模拟结果与相关的实验进行了比较,讨论了各参数对颗粒取向以及沉积率的影响.研究结果表明,随着Stk和颗粒长径比β的增加以及De和Re的减少,颗粒的主轴更趋向于流动方向.颗粒流经弯管时的沉积率随着De,Re和颗粒长径比β的增加而增加,但随Stk的变化呈现非单调趋势,当Stk<7时,沉积率随Stk的增加而减少,当Stk>7时则相反.
圆柱状颗粒流经弯管湍流场时的取向分布和沉积率是一个复杂问题,本研究的数值模拟结果与圆球颗粒的结果进行了一些比较,开展圆柱状颗粒流经弯管湍流场的实验研究是将来需要进行的工作.
参考文献( References ):
[1]AKSHAT T M, MISRA S, GUDIYAWAR M Y, et al.Effect of electrospun nanofiber deposition on thermophysiology of functional clothing[J].Fibers and Polymers, 2019, 20(5): 991-1002.
[2]TIAN L, AHMADI G, WANG Z C, et al.Transport and deposition of ellipsoidal particles in low Reynolds number flows[J].Journal of Aerosol Science, 2012, 45: 1-18.
[3]TU C X, YIN Z Q, LIN J Z, et al.A review of experimental techniques for measuring micro- to nano-particleladen gas flows[J].Applied Sciences, 2017, 7(2).DOI: 10.3390/app7020120.
[4]SUN L, LIN J Z, BAO F B.Numerical simulation on the deposition of nanoparticles under laminar conditions[J].Journal of Hydrodynamics, 2006, 18(6): 676-680.
[5]PHARES D J, SHARMA G.A DNS study of aerosol deposition in a turbulent square duct flow[J].Aerosol Science and Technology, 2006, 40(11): 1016-1024.
[6]ARMAND P, BOULAUD D, POURPRIX M, et al.Two-fluid modeling of aerosol transport in laminar and turbulent flows[J].Journal of Aerosol Science, 1998, 29(8): 961-983.
[7]罗万清, 李海燕, 梁剑寒.基于Euler-Lagrange模型的电弧风洞喷管两相流模拟[J].应用数学和力学, 2020, 41(1):16-26.(LUO Wanqing, LI Haiyan, LIANG Jianhan.Simulation of 2-phase flow in the nozzle of the arc heated wind tunnel based on the Eulerian-Lagrange model[J].Applied Mathematics and Mechanics, 2020, 41(1): 16-26.(in Chinese))
[8]LIN J Z, YIN Z Q, GAN F J, et al.Penetration efficiency and distribution of aerosol particles in turbulent pipe flow undergoing coagulation and breakage[J].International Journal of Multiphase Flow, 2014, 61: 28-36.
[9]PUI D Y H, ROMAY-NOVAS F, LIU B Y H.Experimental study of particle deposition in bends of circular cross section[J].Aerosol Science and Technology, 1987, 7(3): 301-315.
[10]BALÁSHÁZY I, MARTONEN T B, HOFMANN W.Inertial impaction and gravitational deposition of aerosols in curved tubes and airway bifurcations[J].Aerosol Science and Technology, 1990, 13(3): 308-321.
[11]LEE K W, GIESEKE J A.Deposition of particles in turbulent flow pipes[J].Journal of Aerosol Science, 2006,25(4): 699-709.
[12]SATO S, CHEN D R, PUI D Y H.Particle transport at low pressure: deposition in bends of a circular cross-section[J].Aerosol Science and Technology, 2003, 37: 770-779.
[13]WANG J, FLAGAN R C, SEINFELD J H.Diffusional losses in particle sampling systems containing bends and elbows[J].Journal of Aerosol Science, 2002, 33(6): 843-857.
[14]YOOK S J, PUI D Y H.Experimental study of nanoparticle penetration efficiency through coils of circular crosssections[J].Aerosol Science and Technology, 2006, 40(6): 456-462.
[15]LIN J Z, LIN P F, CHEN H J.Research on the transport and deposition of nanoparticles in a rotating curved pipe[J].Physics of Fluid, 2009, 21(12): 122001.
[16]WILSON S R, LIU Y A, MATIDA E A, et al.Aerosol deposition measurements as a function of Reynolds number for turbulent flow in a ninety-degree pipe bend[J].Aerosol Science and Technology, 2011, 45(3): 364-375.
[17]GHAFFARPASAND O, DREWNICK F, HOSSEINIEBALAM F, et al.Penetration efficiency of nanometer-sized aerosol particles in tubes under turbulent flow conditions[J].Journal of Aerosol Science, 2012, 50: 11-25.
[18]LIN J Z, YIN Z Q, LIN P F, et al.Distribution and penetration efficiency of nanoparticles between 8~550 nm in pipe bends under laminar and turbulent flow conditions[J].International Journal of Heat and Mass Transfer,2015, 85: 61-70.
[19]BATCHELOR G K.Slender-body theory for particles of arbitrary cross-section in Stokes flow[J].Journal of Fluid Mechanics, 1970, 44(3): 419-440.
[20]MACKAPLOW M B, SHAQFEH E S G.A numerical study of the sedimentation of fiber suspension[J].Journal of Fluid Mechanics, 1988, 376(1): 149-182.
[21]MICHAELIDES E E.Brownian movement and thermophoresis of nanoparticles in liquids[J].International Journal of Heat and Mass Transfer, 2015, 81: 179-187.
[22]LEAL L G, HINCH E J.The effect of weak Brownian rotations on particles in shear flow[J].Journal of Fluid Mechanics, 1971, 46: 685-703.
[23]高振宇, 林建忠, 李俊.纤维悬浮剪切湍流中纤维旋转扩散系数的理论研究[J].应用数学和力学, 2007, 28(3): 263-269.(GAO Zhenyu, LIN Jianzhong, LI Jun.Theoretical research on the rotational dispersion coefficient of fiber in the turbulent shear flow of fiber suspension[J].Applied Mathematics and Mechanics, 2007, 28(3): 263-269.(in Chinese))
[24]CHEN S B, JIANG L.Orientation distribution in a dilute suspension of fibers subject to simple shear flow[J].Physics of Fluid, 1999, 11(10): 2878-2890.
[25]LIEN F S, LESCHZINER M A.Assessment of turbulence-transport models including non-linear RNG eddy-viscosity formulation and second-moment closure for flow over a backward-facing step[J].Computers and Fluids,1994, 23(8): 983-1004.
[26]LAUNDER B E.Second-moment closure and its use in modeling turbulent industrial flows[J].International Journal for Numerical Methods in Fluids, 1989, 9(8): 963-985.
[27]LAUNDER B E.Second-moment closure: present and future[J].International Journal of Heat and Fluid Flow,1989, 10(4): 282-300.
[28]FUNG J C H, HUNT J C R, MALIK N A, et al.Kinematic simulation of homogeneous turbulence by unsteady random Fourier modes[J].Journal of Fluid Mechanics, 1992, 236: 281-318.
[29]WANG L P, STOCK D E.Numerical simulation of heavy particle dispersion-scale ration and flow decay considerations[J].Journal of Fluids Engineering, 1994, 116(1): 154-163.
[30]DONG S, FENG X, SALCUDEAN M, et al.Concentration of pulp fibers in 3D turbulent channel flow[J].International Journal of Multiphase Flow, 2003, 29(1): 1-21.
[31]WEBSTER D R, HUMPHREY J A C.Experimental observations of flow instability in a helical coil[J].Journal of Fluids Engineering, 1993, 115(3): 436-443.
[32]KRUSHKAL E M, GALLILY I.On the orientation distribution function of nonspherical aerosol particles in a general shear flow, Ⅱ: the turbulent case[J].Journal of Aerosol Science, 1988, 19(2): 197-211.
[33]PODGÓRSKI A, GRADOŃ L, GRZYBOWSKI P.Theoretical-study on deposition of flexible and stiff fibrous aerosol-particles on a cylindrical collector[J].Chemical Engineering Journal and the Biochemical Engineering Journal, 1995, 58(2): 109-121.
