微曲输流管道振动固有频率分析与仿真*

袁嘉瑞， 丁 虎， 陈立群

（上海大学 力学与工程科学学院，上海 200444）

引 言

管道常见于化工、石油、核能和航空航天等领域内的各种工程设施中.受限于飞机结构，管道以各种形式与连接方式遍布于飞机全身，构成复杂的管路系统.在多重激励的耦合作用下，管道在工作过程中不可避免地会产生振动，在内部出现循环应力，致使管道出现疲劳损伤[1]，甚至会在某些极端振动环境下失效而导致液体泄漏并产生严重后果.因此，关于输流管道振动方面的问题一直以来都是热门课题.但是，大部分的研究都聚焦于具有理想结构管道的振动问题[2-11].例如，Ding等针对非线性连续系统，建立了与两个非线性隔振器耦合的输流管道非线性受迫振动动力学模型[12].Tan等基于Timoshenko梁理论，推导出了输流管道非线性耦合偏微分方程，揭示了超临界状态下管道受迫振动的多重共振响应[13].

然而由于加工误差、工程限制或受到长期载荷作用等因素，大多数管道存在初始几何缺陷，会出现轻微弯曲的现象.对于微曲管道的振动特性，很多学者也展开了相关研究，发现这些细小的缺陷会对结构的振动特性产生较大的影响.Ye等研究了流速在超临界范围内的输流微曲管道的横向自由振动特性[14].Akintoye等研究了热载荷作用下不同边界条件对微曲管道非线性动力学的影响[15].Li等研究了输送脉动流体的微曲管道的非线性振动[16].以上的研究都是基于Euler-Bernoulli梁理论对微曲输流管道进行动力学建模，并未考虑剪切变形和转动惯量的影响.而考虑这些因素后的Timoshenko模型不仅在分析短粗管道结构时比Euler-Bernoulli模型精确，而且在分析高频振动，如飞机上管路由于高频激励产生响应的情况时，具有更高的精度.

另一方面，具有复杂结构管道且考虑流体影响的振动问题，难以采用解析或半解析的方法进行分析.而借助有限元软件进行仿真，就能有效地模拟流体与管道之间复杂的耦合方式.ANSYS作为典型的有限元仿真软件[17-18]，其中的湿模态模块可以分析管道充液时的模态.然而，在计入流体速度以后，采用软件中的流固耦合模块进行模态分析时，只能计入流体对管道的压力影响，不能计入流体质量流动产生的影响.因此，无法分析流体流速对管道振动特征的影响.对此，李占营等基于ANSYS二次开发自定义管单元，建立了输流管道的有限元模型，能考虑流体流速的影响[19].随后，李继世等利用ANSYS中现有单元结构的优势，在ANSYS中通过引入自定义刚度、阻尼单元来等效流体流动的影响，实现了计入流体流动影响的管道固有振动特征计算[20].此外，胡效东等基于ANSYS商用软件，研究了管道湿模态振动特性[21]；田晓洁等通过ANSYS中的acoustic extension模块考虑了外部海水的附加质量作用，对气液两相流海洋立管进行了模态分析和动力学分析[22].需要指出的是，上述文献采用有限元软件进行数值分析的管道模型多为等截面的直管，对于常见于工程中的微曲管道的有限元数值仿真分析方法尚需要进一步研究.

本文首先提出了基于Timoshenko梁理论假设的微曲输流管道的动力学模型，通过广义Hamilton原理导出微曲管道横向振动的控制方程.通过Galerkin截断结合广义本征值方法，解析分析了输流管道横向振动的固有频率.基于ANSYS软件，分别用湿模态模块与流体等效影响法对充液与流体有流速的情况进行分析，实现解析分析结果与有限元数值仿真结果的相互验证.

1 理论模型

如图1所示，管道两端为简支边界，其纵向振动幅值微弱，可忽略不计，只考虑管道的横向振动.管道密度为ρp，跨度为L，横截面外径为D，内径为d，截面绕中性轴的转动惯量为Ip，剪切模量为G，弹性模量为E.管内介质为不可压缩流体，密度为ρf，以恒定的流速Γ在管内流动.v为管道的横向位移，Y(x)为管道的初始永久变形，可用正弦函数表示：

图1 微曲管道模型Fig.1 The physical model for a slightly curved pipe

式中A0为初始中点挠度，其值远小于管道跨度，可将管道与流体微元长度近似为dx.则微曲管道与流体的动能分别为

管道的应变势能为

其中σx和εx分别为正应力和Lagrange应变，τyx和γyx分别为表示剪应力和剪应变.管道应变-位移关系为

视管道材料为弹性材料，满足如下关系：

式中ks为Timoshenko管道的横截面形状系数，其定义式为

其中µ 为Poisson比.基于广义Hamilton原理

导出如下微曲管道横向振动的非线性偏微分-积分控制方程组：

略去控制方程中管道材料的非线性项，得到控制方程(8)的线性派生系统：

两端简支的边界条件可以表示为

2 Galerkin截断

将方程(9)的解离散成具有2n个广义坐标的常微分方程组，位移变量的表达式如下:

其中

由于管道为简支边界，ϕv(x)和 ϕφ(x)可选为

根据Galerkin截断思想，将式(13)代入式(9)，然后两式等号两边分别再同时乘以权函数，其形式与试函数相同，即ϕv(x)和 ϕφ(x).然后对x从0到L进行积分，得到如下矩阵形式的表达式：

其中M，G，K分别为积分后得到的质量、陀螺与刚度矩阵.根据系统振动规律，假设q=Qeiωt，Q为一维常数列向量.将其代入式(14)中，得到代数方程组：

上式存在非零解的条件为方程组的系数矩阵H的行列式为零：

确定截断阶数后，即可计算出微曲管道流固耦合振动的固有频率.

3 数值仿真

3.1 湿模态分析

本文采用ANSYS Workbench中的湿模态（modal acoustics）模块仿真计算液体无流速充液状态下的管道振动的固有频率和模态.

3.2 等效流体影响

根据控制方程(9)，考虑流体介质的影响主要为两个方面：质量和流速.在ANSYS中分别采用相应的等效方式：流体质量影响等效为附加质量，而由流速产生的陀螺项以及刚度变化可在仿真软件中分别等效为附加阻尼和附加刚度[17].相应地，考虑单元选择为Pipe288单元（二节点直线型管单元）以及Matrix27单元（自定义单元）.其中附加质量可直接在管单元截面参数中设置：

如图2所示，Lp为单元长度，L0为单元长度的二分之一，Vi，Vj分别为i，j节点沿y轴方向的位移，θz,j分别为i，j节点绕z轴方向的转角.单元中任意一点沿x，y，z三个方向的位移分别用U，V，W表示，其中y方向的位移形式如下：

图2 二节点线（管）单元模型示意图Fig.2 The model for a 2-node line element

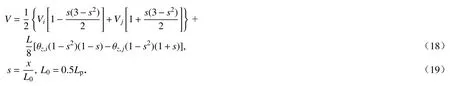
则可以将式(18)写成

式中NT为形函数.由输流微曲管道横向振动的控制方程(9)能够得到附加的等效刚度矩阵Ky为

同理，等效阻尼矩阵Cy为

由于本文仅考虑输流管道在y方向上的横向振动，则x，z方向均无附加刚度、阻尼矩阵.根据ANSYS中的位移阵列模式，节点位移定义为

则整体矩阵阶数应为12，按照上述位移顺序叠加x，y，z三个方向的等效刚度和阻尼矩阵，即可得到整体附加刚度和阻尼矩阵.在ANSYS中设置过程如下：1) 以xOy平面为基础，x方向为纵向，y方向为横向，通过Pipe288单元建立微曲管道的模型.由于管道初始变形远小于管道跨度，则单元两端点因初始变形产生的y轴方向坐标之差可以忽略，可近似认为单元长度等于其两端点的x轴坐标差值.2) 通过Matrix27单元定义相应的等效刚度、等效阻尼单元，并将其分配到每个Pipe288单元的两节点之间.3) 设置边界条件，只考虑约束单元在z轴方向上的自由度，最后，采用modal-QR damp模块进行分析.

4 固有频率

本文算例采用液压管道（1Cr18Ni9），基本参数由表1给出.采用四阶Galerkin截断计算管道的前四阶固有频率，并通过ANSYS软件仿真进行对比验证.

表1 1Cr18Ni9输流管道与流体参数Table 1 Physical parameters of the 1Cr18Ni9 pipe and fluid

图3显示了管道在充液状态下，两种方法求解得到的不同初始中点挠度下固有频率变化曲线，Galerkin截断结果与数值仿真结果几乎一致.结果表明，初始中点挠度对微曲管道的固有频率具有一定的影响，在充液状态时，随着初始弯曲幅度的增加，管道横向振动的固有频率会明显增大.

图3 初始中点挠度对充液状态微曲管道固有频率的影响：（a）第一和第二阶固有频率；（b）第三和第四阶固有频率Fig.3 Effects of the initial deflection on natural frequencies of the slightly curved pipe in a liquid-filled state: (a) the 1st and 2nd natural frequencies;(b) the 3rd and 4th natural frequencies

当考虑管内流体具有流速时，数值仿真过程采用等效流体影响法.图4给出了当流速达到60 m/s时，初始弯曲幅度对微曲管道横向振动固有频率的影响趋势.管道的固有频率变化趋势与充液状态下一致.但是，液体流动的速度会降低管道前四阶固有振动频率.

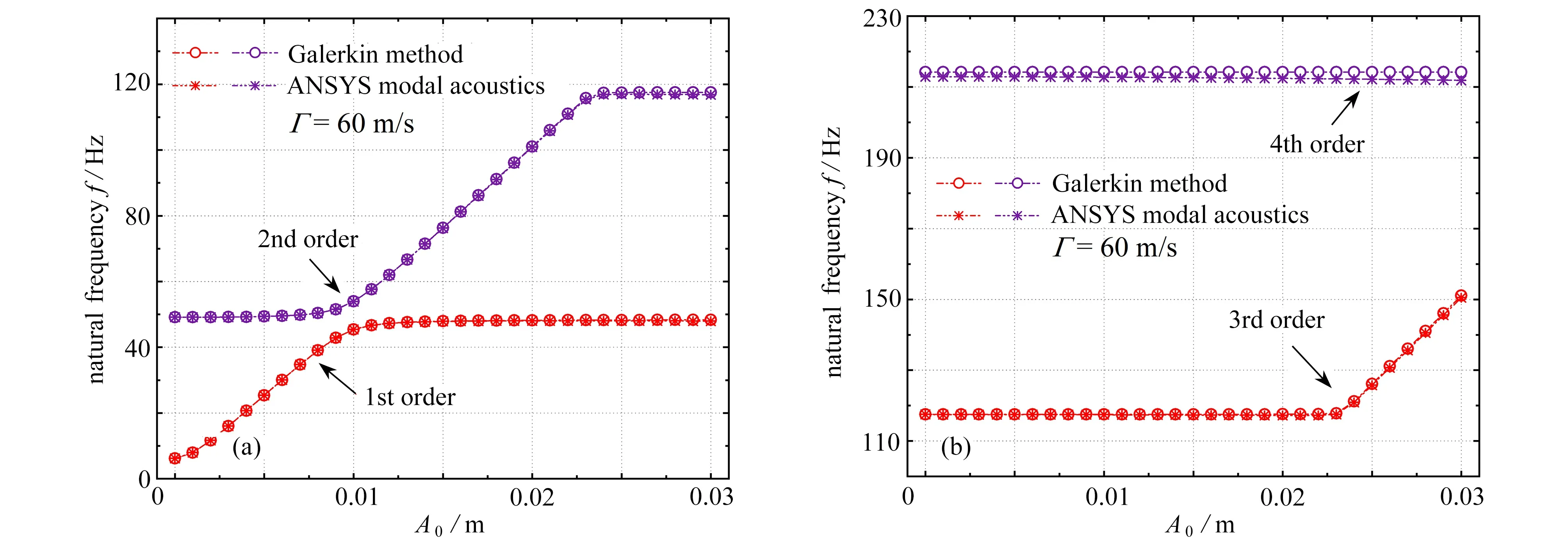
图4 弯曲幅度对微曲输流管道横向振动固有频率的影响：（a）第一和二阶固有频率；（b）第三和第四阶固有频率Fig.4 Effects of the initial deflection on natural frequencies of the slightly curved pipe with flowing fluid: (a) the 1st and 2nd natural frequencies;(b) the 3rd and 4th natural frequencies

图5、图6给出了不同流速下两种方法计算得到的微曲管道横向振动前四阶固有频率的对比.结果显示，微曲管道的固有频率随着管道内流速增大而减小，不同的弯曲幅度都存在临界流速，当达到临界流速时，管道的第一阶固有频率将降低至零.对比发现，较大的初始弯曲幅度会增大管道的临界流速.

图5 流速对微曲管道固有频率的影响（A0=0.003 m）：（a）第一和第二阶固有频率；（b）第三和第四阶固有频率Fig.5 Effects of the fluid velocity on natural frequencies of the slightly curved pipe (A0=0.003 m): (a) the 1st and 2nd natural frequencies;(b) the 3rd and 4th natural frequencies

图6 流速对微曲管道固有频率的影响（A0=0.006 m）：（a）第一和第二阶固有频率；（b）第三和第四阶固有频率Fig.6 Effects of the fluid velocity on natural frequencies of the slightly curved pipe (A0=0.006 m): (a) the 1st and 2nd natural frequencies;(b) the 3rd and 4th natural frequencies

5 结 论

本文以微曲输流管道为研究对象，基于Timoshenko梁理论，考虑了剪切变形与转动惯量的影响，建立了输流管道横向振动的动力学模型.并基于ANSYS采用等效流体影响法建立了计入流速影响的微曲管道模型.发展Galerkin截断与ANSYS数值仿真两种方法分析了管道的固有振动频率，通过对比，验证了本文建立的模型和发展的分析方法的正确性.

探讨了初始弯曲幅度和流体流速对微曲管道横向振动固有频率的影响.研究表明，初始弯曲幅度的增大会导致管道振动的部分阶固有频率增大，在考虑了流体对管道的影响后，微曲管道的固有频率随着管内流体流速的增大而逐渐减小.当流速达到临界时，管道振动的固有频率会降低至零，此时将会处于失稳状态.而且初始弯曲会增大管道的临界流速.总之，初始弯曲变形对输流管道振动特性影响较大.因此，为了获得正确可靠的结果，在分析输流管道的振动特性时，需要计入管道的几何缺陷或初始曲率的影响.

参考文献（ References ）：

［1］武新丽, 罗维东, 吴冬, 等.压力管道破坏的形式、原因与防止[J].中国科技信息, 2005（19）: 29, 46.（WU Xinli,LUO Weidong, WU Dong, et al.The form, cause and prevention of pressure pipe damage[J].China Science and Technology Information, 2005（19）: 29, 46.（in Chinese））

［2］郑哲敏.管道的振动[J].清华大学学报, 1956（1）: 32-36, 286.（ZHENG Zheming.Analysis of pipe vibrations[J].Journal of Tsinghua University, 1956（1）: 32-36, 286.（in Chinese））

［3］朱竑祯, 王纬波, 殷学文, 等.基于分层模型的功能梯度输流管道耦合振动[J].振动与冲击, 2019, 38（20）: 203-209.（ZHU Hongzhen, WANG Weibo, YIN Xuewen, et al.Coupled vibration of functionally graded pipes conveying fluid based on a multi-layered model[J].Journal of Vibration and Shock, 2019, 38（20）: 203-209.（in Chinese））

［4］YAMASHITA K, YAGYU K, YABUNO H.Nonlinear interactions between unstable oscillatory modes in a cantilevered pipe conveying fluid[J].Nonlinear Dynamics, 2019, 98（4）: 2927-2938.

［5］MAO X Y, DING H, CHEN L Q.Steady-state response of a fluid-conveying pipe with 3:1 internal resonance in supercritical regime[J].Nonlinear Dynamics, 2016, 86（2）: 795-809.

［6］TAN X, DING H, CHEN L Q.Nonlinear frequencies and forced responses of pipes conveying fluid via a coupled Timoshenko model[J].Journal of Sound and Vibration, 2019, 455: 241-255.

［7］肖斌, 周玉龙, 高超, 等.考虑流体附加质量的输流管道振动特性分析[J].振动与冲击, 2021, 40（15）: 182-188.（XIAO Bin, ZHOU Yulong, GAO Chao, et al.Analysis of vibration characteristics of pipeline with fluid added mass[J].Journal of Vibration and Shock, 2021, 40（15）: 182-188.（in Chinese））

［8］张挺, 林震寰, 林通, 等.内激励型振荡衰减流作用下输流管道动力不稳定分析[J].振动与冲击, 2021, 40（3）: 284-290.（ZHANG Ting, LIN Zhenhuan, LIN Tong, et al.Dynamic instability analysis of pipeline conveying fluid under action of internally excited oscillation attenuation flow[J].Journal of Vibration and Shock, 2021, 40（3）: 284-290.（in Chinese））

［9］GAO P X, YU T, ZHANG Y L, et al.Vibration analysis and control technologies of hydraulic pipeline system in aircraft: a review[J].Chinese Journal of Aeronautics, 2021, 34（4）: 83-114.

［10］LI Q, LIU W, LU K, et al.Flow-induced buckling statics and dynamics of imperfect pipes[J].Archive of Applied Mechanics, 2021, 91: 4553-4569.

［11］ZHOU K, NI Q, CHEN W, et al.Static equilibrium configuration and nonlinear dynamics of slightly curved cantilevered pipe conveying fluid[J].Journal of Sound and Vibration, 2021, 496: 115711.

［12］DING H, JIN J C, CHEN L Q.Nonlinear vibration isolation for fluid-conveying pipes using quasi-zero stiffness characteristics[J].Mechanical Systems and Signal Processing, 2019, 121: 675-688.

［13］TAN X, DING H, SUN J Q, et al.Primary and super-harmonic resonances of Timoshenko pipes conveying highspeed fluid[J].Ocean Engineering, 2020, 203: 107258.

［14］YE S Q, DING H, WEI S, et al.Non-trivial equilibriums and natural frequencies of a slightly curved pipe conveying supercritical fluid[J].Ocean Engineering, 2021, 227: 108899.

［15］AKINTOYE O O, OYEDIRAN A A.The effect of various boundary conditions on the nonlinear dynamics of slightly curved pipes under thermal loading[J].Applied Mathematical Modelling, 2020, 87: 332-350.

［16］LI Y D, YANG Y R.Nonlinear vibration of slightly curved pipe with conveying pulsating fluid[J].Nonlinear Dynamics, 2017, 88（4）: 2513-2529.

［17］刘燕, 张伟, 龚涛涛.轴向可伸缩复合材料悬臂梁的非线性振动研究[J].动力学与控制学报, 2020, 18（4）: 19-25.（LIU Yan, ZHANG Wei, GONG Taotao.Modeling and numerical analysis of an axially moving composite laminated cantilever beam[J].Journal of Dynamics and Control, 2020, 18（4）: 19-25.（in Chinese））

［18］王松松, 郭翔鹰, 王帅博.变截面Z型折叠机翼振动特性的有限元与实验分析[J].动力学与控制学报, 2020, 18（6）:84-89.（WANG Songsong, GUO Xiangying, WANG Shuaibo.Finite element and experimental analysis of vibration characteristics of variable cross-section Z-form folding wing[J].Journal of Dynamics and Control, 2020,18（6）: 84-89.（in Chinese））

［19］李占营, 王建军, 邱明星.航空发动机空间管路系统的流固耦合振动特性[J].航空动力学报, 2016, 31（10）: 2346-2352.（LI Zhanying, WANG Jianjun, QIU Mingxing.Dynamic characteristics of aero-engine pipe system considering fluid-structure coupling[J].Journal of Aerospace Power, 2016, 31（10）: 2346-2352.（in Chinese））

［20］李继世, 张大义, 王立, 等.考虑流体介质影响的管路模态特性分析[J].航空动力学报, 2019, 34（3）: 671-677.（LI Jishi, ZHANG Dayi, WANG Li, et al.Modal characteristics analysis for pipelines considering influence of fluid medium[J].Journal of Aerospace Power, 2019, 34（3）: 671-677.（in Chinese））

［21］胡效东, 梁泽华, 宗丹丹, 等.湿模态管道振动特性研究[J].机械设计与制造, 2021（8）: 300-304.（HU Xiaodong, LIANG Zehua, ZONG Dandan, et al.Study on vibration characteristics of wet-mode pipeline[J].Machinery Design& Manufacture, 2021（8）: 300-304.（in Chinese））

［22］田晓洁, 谢大帅, 刘贵杰, 等.基于ANSYS的气液两相流海洋立管流固耦合特性分析[J].振动与冲击, 2021, 40（7）:260-267.（TIAN Xiaojie, XIE Dashuai, LIU Guijie, et al.Analysis of fluid-structure interaction characteristics of gas-liquid two-phase flow marine riser based on ANSYS[J].Journal of Vibration and Shock, 2021, 40（7）: 260-267.（in Chinese））