细观等效理论预测再生混凝土宏观力学参数*

陈海玉， 徐福卫

（湖北文理学院 土木工程与建筑学院，湖北 襄阳 441053）

引 言

再生混凝土（recycled aggregate concrete, RAC）由水泥、砂子、原生骨料（aggregate, AG）及再生骨料（recycled aggregate，RAG）通过水化反应胶凝而成，相较于普通混凝土，其孔隙、微裂缝及裂纹体积分数明显增加[1].从细观层次看，普通混凝土可看成由原生骨料、界面过渡区和水泥砂浆组成的三相复合材料[2]；再生骨料表面附着有老水泥砂浆，因此从里到外，再生混凝土可以看作是由原生骨料、老界面层（old ITZ，OI）、老水泥砂浆（old cement mortar, OCM）、新界面层（new ITZ，NI）和新水泥砂浆（new cement mortar, NCM）[3]组成的五相复合材料.若将老界面层、老水泥砂浆和新界面层合成一个界面过渡区（interfacial transition zone，ITZ），再生混凝土亦可以看成是由原生骨料、界面过渡区和新水泥砂浆组成的三相复合材料.再生混凝土的界面过渡区和新水泥砂浆中含有较多的孔隙、微裂缝和裂纹，再生混凝土又可看成由原生骨料、界面过渡区、新水泥砂浆和孔隙组成的四相复合材料.

针对再生混凝土的宏观力学性能，国内外学者开展了众多的研究，取得了丰富的成果[4-9]，文献[10]在进行细观数值分析时将再生混凝土分成了原生骨料、界面过渡区和新水泥砂浆，但没有从细观组分的角度分析各组分对再生混凝土宏观力学参数的影响.根据复合材料中单个材料组分的性能和相对数量预测复合材料有效宏观力学参数，是进行复合材料力学分析的基本问题[11].预测复合材料的宏观力学参数最理想的方法是选择具有代表意义的典型体积单元进行应力和变形分析[12]，通过应力应变关系可以得到比较理想的结果.1889年和1929年，Voigt[13]和Reuss[14]分别提出了并联和串联弹模等效模型，这两种模型被广泛用于复合材料宏观力学参数的预测.后来自一致性方法[15]、田中音步方法[16]、最终估计方法[17]和PFM方法[18]等许多经典的均质化方法相继被提出，应用于非均质材料有效宏观力学参数的预测.1993年，Huang和Gibson[19]提出了一种用空心球分析复合材料有效弹模的数学方法.Paul[20]采用最小势能和最小余能原理得到了各向同性材料的弹性常数的上限和下限.Zimmerman等[21]和Yaman等[22]采用K-T模型研究了孔隙率对水泥砂浆弹性参数的影响，并将实验观察结果与理论结果进行了比较.Sanahuja等[23]将无序介质进行均化，利用匀质理论预测了水泥砂浆有效弹性模量的演变.李天一等[24]采用图像数字技术获得了混凝土试件内部细观结构，数值分析了骨料的形态、分布和体分比对混凝土强度的影响.陈青青等[25]采用入侵判定算法建立了含孔隙的混凝土细观模型.以上细观力学方法和模型采用不同的有效介质，近似考虑了夹杂物之间的弹性相互作用以预测复合材料的弹性参数，却忽略了各弹性参数之间的联系，预测的弹性参数也不够理想.

研究再生混凝土各细观组分对再生混凝土宏观力学参数的影响，对再生混凝土的数值仿真和配合比的设计具有重要意义.如何定量描述各组分（相）对再生混凝土宏观力学参数的影响，以及如何确定再生骨料掺量和孔隙率与再生混凝土宏观力学性能之间的定量关系等，还没有明确的结论.为了研究再生混凝土各组分、各相对其宏观力学参数的影响，本文假设再生骨料都是圆形或球形骨料，建立空心圆柱或空心球模型，利用扭转变形原理、细观等效理论和应力应变关系，推导了再生混凝土宏观等效力学参数的预测模型.

1 再生混凝土宏观等效力学参数推导

1.1 再生混凝土界面过渡区宏观等效力学参数

再生混凝土界面过渡区由老界面层、老水泥砂浆和新界面层三个层次组成.老界面层、老水泥砂浆和新界面层三者的各项材料性能比较接近，都具有较高的孔隙率，Poisson比十分接近，而这三个层次的材料从骨料表面依次黏结，从力学模型分析，符合Reuss串联模型，因此按照串联模型进行界面过渡区等效Poisson比

式中，fOI，fOM，fNI和 µOI，µOCM，µNI分别为老界面层、老水泥砂浆和新界面层的体分比和Poisson比.

为了求解界面过渡区的等效剪切模量，建立空心圆柱等效模型，将组成界面过渡区的三层组份看成是空心圆柱的三层圆环，如图1所示.

图1 界面过渡区空心圆柱等效模型Fig.1 The equivalent model for the hollow cylinder in the interfacial transition zone

根据肖建庄等[10]的研究结果，由不同强度废弃混凝土生产的再生骨料，老水泥砂浆的含量为40%左右.图1中的再生骨料中原生骨料粒径（RAG）为5 ～ 25 mm、老界面层厚度为50 µm，折算后不同骨料外面包裹的老水泥砂浆厚度为1.10 mm左右，新界面层厚度为50 µm.

假定空心圆柱在外力偶作用下各层之间无相对滑动，各层共同承担扭转力矩(式(3))，且扭转变形时具有相同的相对扭转角(式(4))，因此，借助扭转变形理论，空心圆柱各层组分的极惯性矩可以表述成下述形式(式(5))：

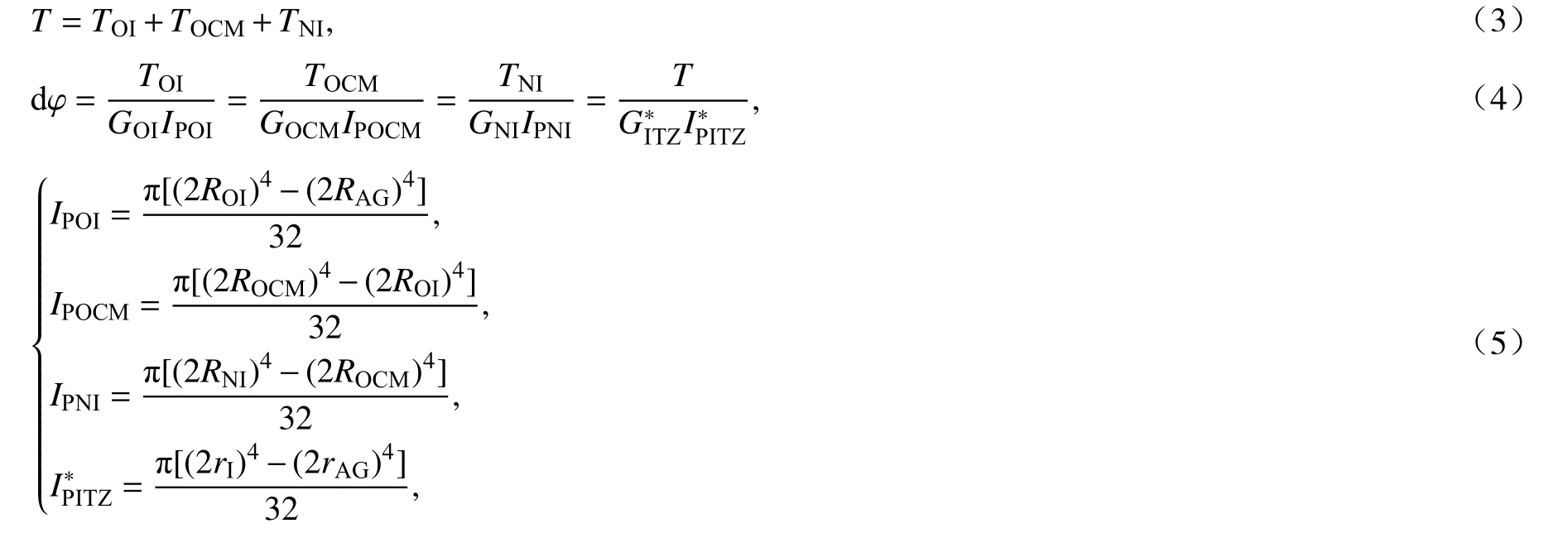
式中，T为界面过渡区整体和每层的扭矩；I为界面过渡区整体和每层的极惯性矩；G为 界面过渡区整体和每层的剪切模量；R为每层的内外半径.

由式（3）和（4）可求得等效界面过渡区的剪切模量

将式（5）代入式（6），求得剪切模量的具体表达式：

因此，老界面层、老水泥砂浆和新界面层组成的三层介质等效成一层厚度均匀的界面过渡区(如图2)，可以定量分析界面过渡区的宏观力学参数.

图2 界面过渡区均化等效示意图Fig.2 The homogenized equivalent schematic diagram of the interfacial transition zone

1.2 混凝土粗骨料的宏观等效力学参数

再生混凝土含有两类骨料，一类是再生骨料，一类是普通骨料.再生骨料是由原生骨料和界面过渡区（包含老界面层、老水泥砂浆和新界面层）组成，普通骨料由原生骨料和新界面层组成.建立由原生骨料为内层，界面过渡区（界面过渡层）为外层的骨料空心圆柱等效模型（如图3），假设骨料处于弹性状态下，内外层在外力偶矩的作用下具有相同的相对扭转角，从而求得再生粗骨料和普通骨料的等效剪切模量：

图3 骨料实心圆柱等效模型Fig.3 The equivalent model for the solid cylinder of recycled aggregates

界面过渡区包裹在原生骨料外面，受力过程符合Reuss的串联弹模等效模型.再生骨料四周承受水泥砂浆传来的应力，忽略各组分材料的横向变形，建立再生混凝土骨料横向串联弹模等效模型，因此再生骨料和普通骨料的等效Poisson比分别如式（12a）和（13a）所示：

再生骨料按照一定比例掺入原生骨料，与水泥、砂、水、添加料等拌和制备成再生混凝土，再生粗骨料和普通骨料的受力过程符合Voigt并联模型，可求解再生混凝土骨料的等效弹模和体积模量：

同理，可求得Poisson比和剪切模量：

骨料良好的级配有利于降低混凝土的孔隙率，根据混凝土用途的不同，对混凝土的级配要求也不一样.混凝土骨料都是由不同粒径的骨料按照一定的比例进行配置而成的，Walraven等[26]对Fuller提出的最大密度曲线理论进行了进一步优化，给出了不同粒径骨料累计体分比：

式中，代 表最大粒径骨料的半径值，Pr代表骨料半径小于r0的累计体分比，Pk一 般取0.75.对式（16）微分，可以得到不同粒径骨料在整个骨料中的体分比：

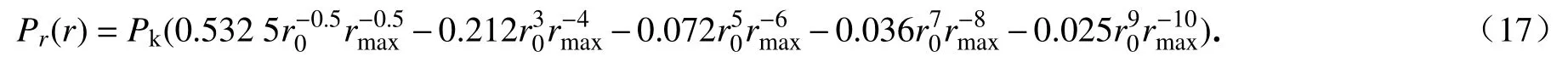
将体分比进行变换，可得到不同粒径骨料颗粒的占比：

式中，rmax，rmin分别为骨料的最大和最小半径.

应用统计学的理论可求得粗骨料的平均半径：

得到了混凝土骨料的平均粒径，则可求解得到混凝土骨料的平均粒径的Poisson比弹性模量剪切模量和体积模量

1.3 再生混凝土等效力学参数的求解

上述推导过程将界面过渡区与原生骨料等效成了再生骨料，此时可将再生混凝土看成再生骨料与新水泥砂浆组成的两相复合材料，再建立实心圆柱横向串联模型，可求解相应的剪切模量和Poisson比，从而求解再生混凝土等效的体积模量和弹性模量：

式中，GRAC， µRAC，ERAC和KRAC分别为再生混凝土等效基材的剪切模量、Poisson比、弹性模量和体积模量；GNCM，IPNCM分别为新水泥砂浆的剪切模量和极惯性矩；fNCM分别为再生混凝土骨料和新水泥砂浆的体分比.

1.4 多孔再生混凝土宏观等效力学参数

再生混凝土的宏观力学参数是混凝土整体宏观变形特性的反映.与应力分布和应力集中相反，等效模量对基体中小区域的局部几何量和物理量的变化不敏感.等效弹性模量和 体积模量可以通过平均法求得.为了获得再生混凝土的等效力学参数，假设再生混凝土由再生混凝土基材和孔隙两相材料组成，建立多孔再生混凝土简化模型（如图4所示）.根据M-T模型的均化思想，建立由一个单一的复合球体包含嵌入无限力学性能未知介质的三相球分析模型，再生混凝土基体设为基质材料，即Ωm区域，它的弹性常数用下标m表示，基材内部区域Ωp表示微裂纹或气孔，基材嵌入其外部等效均匀无限延伸Ωeq的区域，空心弹性球的内外半径分别为a和b.

图4 多孔水泥砂浆简化模型Fig.4 The simplified model for porous cement mortar

将三相球中的孔隙夹杂视为体积和剪切模量可忽略的固体材料.图5为外施均匀拉伸载荷F作用下的空心球分析模型，其中水泥砂浆基体为各向同性、均匀性和弹性.因此，在宏观尺度上，多孔水泥砂浆可以看作是准均质和准各向同性的.

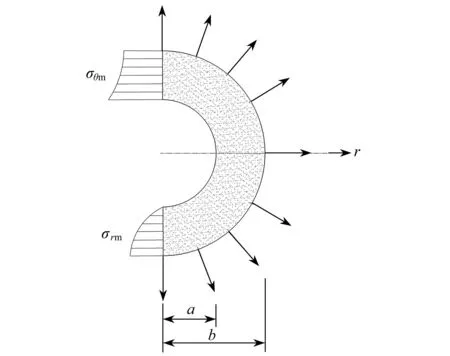
图5 空心球模型图Fig.5 The hollow ball model

从弹性空心球中取出一个六面体微单元，其应力状态如图6所示.在图中， σr为径向应力， σθ为环向应力，Kr表示辐射体的力量.由于几何形状和载荷作用均是对称的，微单元内不产生剪切应力.三相球的受力属于轴对称力学问题，忽略体力影响，在球极坐标系统下的偏微分方程为

图6 微单元的应力状态Fig.6 The stress state of the microelement

式中，ur表示球的径向位移.

球对称问题只有径向位移，其只与半径r有关，与φ 和 θ无关.因此根据微分方程的求解、空间几何关系和物理关系，可得位移分量和应力分量：

式中，A，B为待定系数.

引入球内外边界条件：

将式（28）、（29）的边界条件代入式（22），可得

式中，P为孔隙率，在三相球模型中，P=a3/b3.

等效剪切模量可通过建立孔隙和再生混凝土基材组成的两相空心圆柱等效模型求解，如图7所示.

图7 再生混凝土空心圆柱等效模型：（a）空心圆柱模型；（b）等效模型Fig.7 The equivalent model for the recycled concrete hollow cylinder: （a）the hollow cylinder model; （b）the equivalent model

由于孔隙不承担扭转荷载，整个截面的极惯性矩也就等于空心圆环的极惯性矩，从而得到整个截面的等效剪切模量：

式中，为 多孔再生混凝土的等效剪切模量，β0为空心圆柱的内外径之比.

孔隙所占据的体积相当于圆柱的内部空心圆柱，由于是空心圆柱等效模型，内部空心圆柱与整个圆环的体分比也就是横截面上的面积比，可得P=a2/b2，从而求得新水泥砂浆的等效剪切模量：

2 算例分析

为了验证以上细观等效方法的有效性，我们将预测结果与相关试验结果进行对比.现有相关实验研究主要集中在再生骨料取代率对再生混凝土力学参数的结果，肖建庄等[10]的研究结果表明再生骨料表面附着老水泥砂浆的质量占整个再生骨料的40.4%～45%，因此先要理清再生骨料取代率对再生混凝土孔隙率的影响.文献[27-29]的研究结果表明，随着再生骨料取代率的增加，再生混凝土中水泥砂浆的含量不断增加，其孔隙率也随之增加，如图8所示.再生混凝土总孔隙率随着再生骨料的增加由 9.8%增至 22.5%，是普通混凝土的2.29倍.对文献[25-27]的试验研究数据进行回归分析，得到如式（35）所示的再生骨料取代率与再生混凝土孔隙率的关系式，从而可以定量分析再生骨料的取代率对再生混凝土孔隙率的影响：

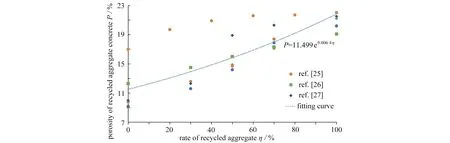
图8 再生骨料取代率对再生混凝土孔隙率的影响Fig.8 Effects of the recycled aggregate replacement rate on the recycled aggregate concrete porosity

式中，P为再生混凝土孔隙率；η为再生骨料取代率.

根据文献[10, 30-31]的研究结果，考虑到再生骨料表面附着老水泥砂浆的质量占整个再生骨料的40.4%～45%，本文假定再生粗骨料中老砂浆的质量占比42%，并根据体积密度关系将质量比换算成体分比，具体见表1.

表1 再生混凝土各组分材料参数表Table 1 Material parameters of recycled aggregate concrete

Yaman和Hearn等[22,32]利用实验得到了某普通高强混凝土不同孔隙率下的弹性模量.王海龙等[33]采用夹杂理论和M-T均化等效思想预测了不同孔隙率下等效弹性模量.文献[34-35]的试验研究结果表明，随着再生骨料取代率的增加，再生混凝土的弹性模量也随之降低.Ravindrarajah等[36]、周静海等[37]和宋灿等[5]的研究结果都发现了相似的现象.对上述研究结果的数据进行分析，与本文的预测结果进行对比，可以看出，试验研究结果与预测结果之间还是比较吻合的，试验结果的趋势线与预测曲线的吻合度还是较好的（如图9和图10所示），说明本理论预测方法和结果是有效的.实验数据的趋势线与预测曲线确实还存在一定的差异，可能是由于收集的研究结果数据量不够大的原因所致.图11显示了再生骨料取代率对再生混凝土Poisson比的影响，图12显示了孔隙率对再生混凝土的弹性模量与剪切模量影响趋势，也就是随着再生骨料取代率的增加，再生混凝土中水泥砂浆的含量也不断增加，孔隙率不断增加，再生混凝土的Poisson比随之不断增加，剪切模量和体积模量的都在不断降低，其主要原因是孔隙率存在于水泥砂浆中，孔隙的增加相应地就减少了水泥砂浆的含量，从而削弱了再生混凝土的力学性能.

图9 等效弹性模量的预测结果与相关文献数据对比情况Fig.9 Prediction results of the effective elastic modulus and experimental results from relevant literatures

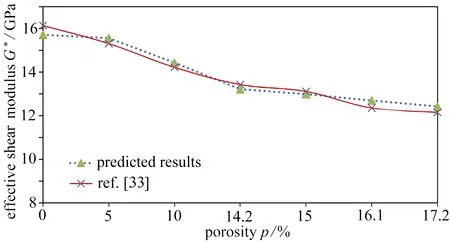
图10 等效剪切模量的预测结果与相关文献数据对比情况Fig.10 Prediction results of the effective shear modulus and experimental results from relevant literature

图11 再生取代率对再生混凝土等效Poisson比的影响Fig.11 Effects of the recycled aggregate replacement rate on effective Poisson’s ratio of the recycled aggregate concrete

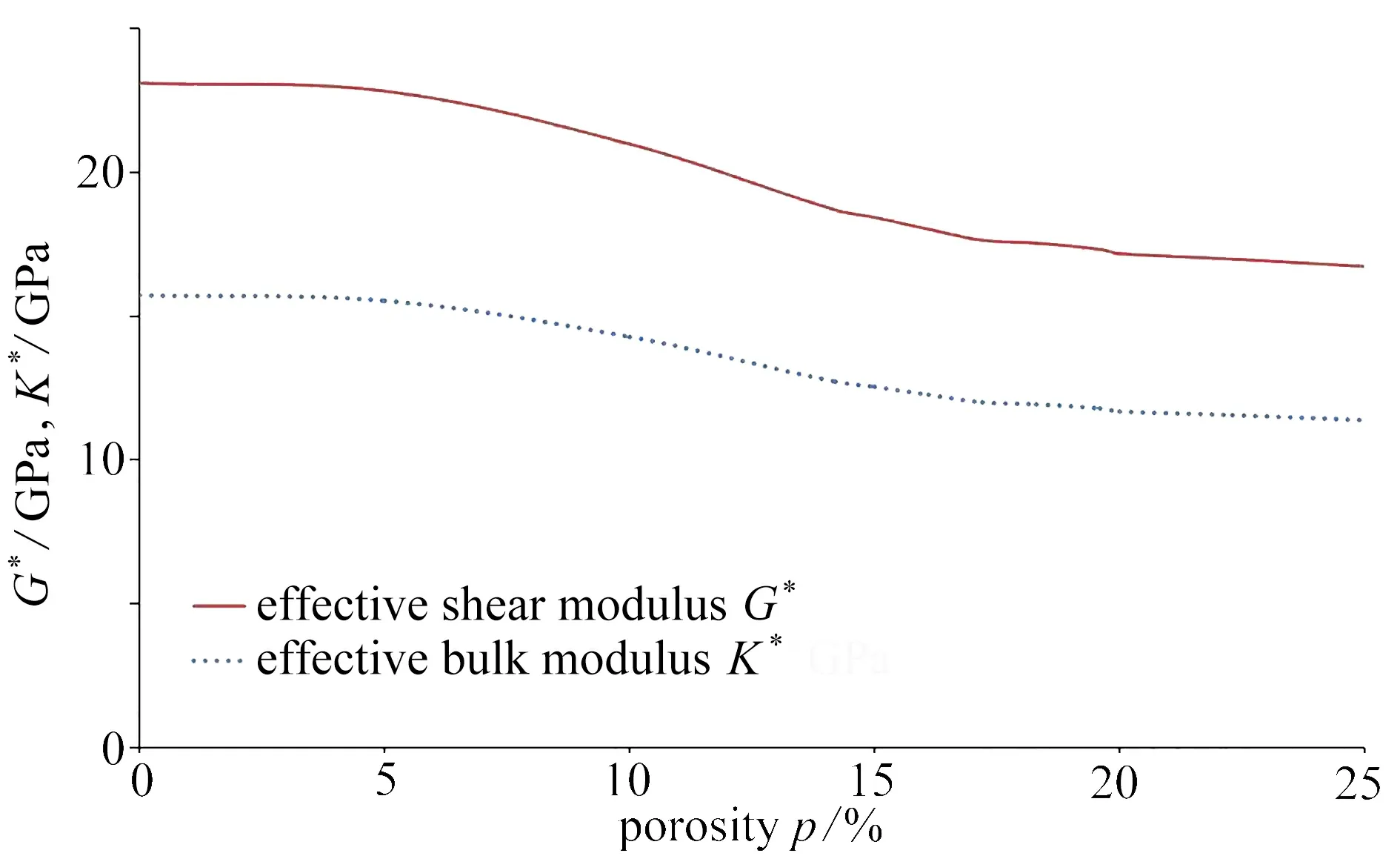
图12 孔隙率对再生混凝土等效剪切模量和体积模量的影响Fig.12 Effects of the porosity on the effective shear modulus and volume modulus of the recycled aggregate concrete

3 结 论

本文证明了利用扭转变形原理、串并联模型以及M-T模型的方法进行再生混凝土的弹性参数的等效预测是可行的.该方法相对比较简单，物理意义明确，为再生混凝土宏观力学参数的预测提供了一条简单实用的新方法，有利于再生混凝土基本力学性能的研究分析.

再生骨料由于自身的弱点，掺入天然骨料中制备再生混凝土，随着再生骨料取代率的增加，再生混凝土的水泥砂浆的含量也不断增加，其孔隙率也随之增加，从而影响再生混凝土的Poisson比不断增加，弹性模量、剪切模量和体积模量不断减少.模型的预测结果较好地反映了再生混凝土宏观力学参数随再生骨料取代率的增加不断变化的这一变化趋势.

参考文献（ References ）：

［1］李佳彬, 肖建庄, 孙振平.再生粗骨料特性及其对再生混凝土性能的影响[J].建筑材料学报, 2004, 7（4）: 390-395.（LI Jiabin, XIAO Jianzhuang, SUN Zhenping.Properties of recycled coarse aggregate and its influence on recycled concrete[J].Journal of Building Materials, 2004, 7（4）: 390-395.（in Chinese））

［2］李冬, 金浏, 杜修力, 等.骨料级配对二维模型混凝土单轴抗拉强度影响的理论研究[J].工程力学, 2017, 34（6）: 64-72.（LI Dong, JIN Liu, DU Xiuli, et al.A theoretical study on the influence of aggregate gradation on the tensile strength of 2-dimensional model concrete[J].Engineering Mechanics, 2017, 34（6）: 64-72.（in Chinese））

［3］王耀, 赵华玮, 胥民尧, 等.基于基面力概念的不同再生骨料取代率混凝土细观损伤研究[J].混凝土, 2018（7）: 76-80.（WANG Yao, ZHAO Huawei, XU Minyao, et al.Research on mesoscopic damage of concrete with different recycled aggregate replacement ratios based on base force element method[J].Concrete, 2018（7）: 76-80.（in Chinese））

［4］胡敏萍.不同取代率再生粗骨料混凝土的力学性能[J].混凝土, 2007（2）: 52-54.（HU Minping.Mechanical properties of concrete prepared with different recycled coarse aggregates replacement rate[J].Concrete, 2007（2）: 52-54.（in Chinese））

［5］宋灿, 陈爱玖.再生粗骨料对再生混凝土基本性能的影响[J].煤炭技术, 2011, 30（6）: 159-161.（SONG Can, CHEN Aijiu.Effect of recycled coarse aggregate on fundamental propertied of recycled concrete[J].Coal Technology,2011, 30（6）: 159-161.（in Chinese））

［6］XIAO J, LI W, CORR D J, et al.Simulation study on the stress distribution in modeled recycled aggregate concrete under uniaxial compression[J].Journal of Materials in Civil Engineering, 2013, 25（4）: 504-518.

［7］LASERNA S, MONTERO J.Influence of natural aggregates typology on recycled concrete strength properties[J].Construction and Building Materials, 2016, 115: 78-86.

［8］HE A, CAI J, CHEN Q J, et al.Axial compressive behaviour of steel-jacket retrofitted RC columns with recycled aggregate concrete[J].Construction and Building Materials, 2017, 141: 501-516.

［9］霍洪媛, 范程程, 陈爱玖.不同强度等级的再生骨料对再生混凝土基本力学性能影响[J].混凝土, 2017（2）: 60-62,65.（HUO Hongyuan, FAN Chengcheng, CHEN Aijiu.Influence of the recycled aggregate with different strength on recycled concrete[J].Concrete, 2017（2）: 60-62,65.（in Chinese））

［10］肖建庄, 刘琼, 李文贵, 等.再生混凝土细微观结构和破坏机理研究[J].青岛理工大学学报, 2009, 30（4）: 24-30.（XIAO Jianzhuang, LIU Qiong, LI Wengui, et al.On the micro- and meso-structure and failure mechanism of recycled concrete[J].Journal of Qingdao Technological University, 2009, 30（4）: 24-30.（in Chinese））

［11］CHRISTENSEN R M, LO K H.Solutions for effective shear properties in three phase sphere and cylinder models[J].Journal of the Mechanics and Physics of Solids, 1979, 27（4）: 315-330.

［12］LEE K J, WESTMANN R A.Elastic properties of hollow-sphere-reinforced composites[J].Journal of Composite Materials, 1970, 4（2）: 242-252.

［13］VOIGT W.Ueber die beziehung zwischen den beiden elasticitätsconstanten isotroper körper[J].Annalen der Physik, 1889, 274（12）: 573-587.

［14］REUSS A.Berechnung der fliessgrenze von Mischkristallen auf grund der plastizitatsbedingung für einkristalle[J].ZAMM Journal of Applied Mathematics & Mechanics Ztschrift fur Angewandte Mathematik und Mechanik, 1929, 9: 49-58.

［15］HILL R.A self-consistent mechanics of composite materials[J].Journal of the Mechanics and Physics of Solids,1965, 13（4）: 213-222.

［16］MORI T, TANAKA K.Average stress in the matrix and average elastic energy of materials with misfitting inclusions[J].Acta Metallurgica, 1973, 21（5）: 571-574.

［17］ZHENG Q S, DU D X.An explicit and universally applicable estimate for the effective properties of multiphase composites which accounts for inclusion distribution[J].Journal of the Mechanics and Physics of Solids, 2001,49（11）: 2765-2788.

［18］NI Y, CHIANG M.Prediction of elastic properties of heterogeneous materials with complex microstructures[J].Journal of the Mechanics and Physics of Solids, 2007, 55: 517-532.

［19］HUANG J S, GIBSON L J.Elastic moduli of a composite of hollow spheres in a matrix[J].Journal of the Mechanics and Physics of Solids, 1993, 41（1）: 55-75.

［20］PAUL B.Prediction of elastic constants of multiphase materials[J].Transactions of the AIME, 1959, 218: 1-19.

［21］ZIMMERMAN R W, KING M S, MOMTERIO P J M.The elastic modulus of mortar as a porous granular material[J].Cement & Concrete Research, 1986, 16（2）: 239-245.

［22］YAMAN I O, AKUAN H M, HEARN A.Active and non-active porosity in concrete part Ⅱ: evaluation of existing models[J].Materials and Structures, 2002, 35（2）: 110-116.

［23］SANAHUJA J, DORMIRUC M, CHANVILLARD G.Modelling elasticity of a hydrating cement paste[J].Ce-ment & Concrete Research, 2007, 37（10）: 1427-1439.

［24］李天一, 章青, 夏晓舟, 等.考虑混凝土材料非均质特性的近场动力学模型[J].应用数学和力学, 2018, 39（8）: 913-924.（LI Tianyi, ZHANG Qing, XIA Xiaozhou, et al.A peridynamic model for heterogeneous concrete materials[J].Applied Mathematics and Mechanics, 2018, 39（8）: 913-924.（in Chinese））

［25］陈青青, 张煜航, 张杰, 等.含孔隙混凝土二维细观建模方法研究[J].应用数学和力学, 2020, 41（2）: 182-194.（CHEN Qingqing, ZHANG Yuhang, ZHANG Jie, et al.Study on a 2D mesoscopic modeling method for concrete with voids[J].Applied Mathematics and Mechanics, 2020, 41（2）: 182-194.（in Chinese））

［26］WALRAVEN J C, REINHARDT H W.Theory and experiments on the mechanical behaviour of cracks in plain and reinforced concrete subjected to shear loading[J].HERON, 1991, 26（1A）: 26-35.

［27］张金喜, 张建华, 邬长森.再生混凝土性能和孔结构的研究[J].建筑材料学报, 2006, 9（2）: 142-147.（ZHANG Jinxi,ZHANG Jianhua, WU Changsen.Study on properties and pore structure of recycled concrete[J].Journal of Building Material, 2006, 9（2）: 142-147.（in Chinese））

［28］张剑波, 吴勇生, 孙可伟, 等.再生骨料混凝土孔隙结构的试验研究[J].硅酸盐通报, 2011, 30（1）: 239-244.（ZHANG Jianbo, WU Yongsheng, SUN Kewei, et al.Experiment and study on pore structure of recycled aggregate concrete[J].Bulletin of the Chinese Ceramic Society, 2011, 30（1）: 239-244.（in Chinese））

［29］余波, 刘才勇, 杨绿峰.再生粗骨料混凝土的孔隙率计算模型[J].混凝土, 2017（11）: 31-34.（YU Bo, LIU Caiyong,YANG Lüfeng.Computing model for porosity of recycled coarse aggregate concrete[J].Concrete, 2017（11）: 31-34.（in Chinese））

［30］沈大钦.再生骨料混凝土性能的研究[D].硕士学位论文.北京: 北京交通大学, 2006.（SHEN Daqin.Study of recycled aggregate concrete[D].Master Thesis.Beijing: Beijing Jiaotong University, 2006.（in Chinese））

［31］袁飚.再生混凝土抗压抗拉强度取值研究[D].硕士学位论文.上海: 同济大学, 2007.（YUAN Biao.On values of compressive strength and tensile strength of recycled aggregate concrete[D].Master Thesis.Shanghai: Tongji University, 2007.（in Chinese））

［32］YAMAN I O, HEARN N, AKTAN H M.Active and non-activ eporosity in concrete, part Ⅰ: experimental evidence[J].Material and Structure, 2002, 35（3）: 102-109.

［33］王海龙, 李庆斌.饱和混凝土的弹性模量预测[J].清华大学学报(自然科学版), 2005, 45（6）: 761-763,775.（WANG Hailong, LI Qingbin.Saturated concrete elastic modulus prediction[J].Journal Tsinghua University(Science and Technology), 2005, 45（6）: 761-763,775.（in Chinese））

［34］金昌.再生混凝土力学性能指标试验研究[D].硕士学位论文.武汉: 武汉理工大学, 2008.（JIN Chang.Experimental research on mechanical performance indexes of recycled concrete[D].Master Thesis.Wuhan: Wuhan University of Technology, 2008.（in Chinese））

［35］中华人民共和国住房和城乡建设部, 中华人民共和国国家质量监督检验检疫总局.混凝土结构设计规范:GB50010—2010[S].北京: 中国建筑工业出版社, 2011.（Ministry of Housing and Urban-Rural Development of the People’s Republic of China, General Administration of Quality Supervision, Inspection and Quarantine of the People’s Republic of China.Code for design of concrete structures: GB50010—2010[S].Beijing: China Architecture&Building Press, 2011.（in Chinese））

［36］RAVINDRARAJAH R, TAM C T.Properties of concrete made with crushed concrete as coarse aggregate[J].Magazine of Concrete Research, 1985, 37（130）: 29-38.

［37］周静海, 何海进, 孟宪宏, 等.再生混凝土基本力学性能试验[J].沈阳建筑大学学报(自然科学版), 2010, 26（3）: 464-467.（ZHOU Jinghai, HE Haijin, MENG Xianhong, et al.Basic mechanical properties of recycled concrete experimental study[J].Journal of Shenyang Jianzhu University(Natural Science), 2010, 26（3）: 464-467.（in Chinese））