基于四阶段应力-应变模型的深部巷道围岩弹塑性分析
2022-07-20李龙清
韩 征,李龙清
(1.中煤西安设计工程有限责任公司,陕西 西安 710054;2.西安科技大学 能源学院,陕西 西安 710054)
0 引 言
随着我国浅部煤炭资源的不断较少,为满足经济高速发展需求,煤炭开采表现出由东部向西部,由浅部向深部转移开采。然而,深部巷道围岩受“三高一扰动”的影响,极易表现出破裂范围广、变形大、支护结构严重失效等破坏特征;尤其对于软岩巷道,开挖后存在明显破裂区,且破裂区范围受开采扰动将不断增大[1-2]。围岩状态分布特征是评价深部巷道整体稳定性与定量支护设计可靠性的理论依据[3-5],岩石峰后破坏的力学行为又是确定围岩状态变化的重要基础,因此选取合理的峰后破坏模型,可使围岩状态的解析解更加接近于工程实际。
关于巷道围岩弹塑性分析问题首先由Fenner提出,之后Kastner进行了修正,但两者均将围岩视为理想弹塑性体,且忽略了峰后应变软化对围岩状态变化的影响。近年来,许多学者采用Mohr-Coulomb(M-C)或者Hoek-Brown(H-B)准则,结合理想弹塑性模型(简称EPM)、弹-脆塑模型(简称EBM)或应变软化模型(简称ESM)进行围岩弹塑性分析,但均忽略了中间主应力的影响[4-10]。试验表明,当考虑中间主应力对岩体屈服的影响时,其强度将提高30%左右[11-12]。张小波等[13]基于Drucker-Prager(D-P)准则,考虑中间主应力的影响,求得了围岩应力、变形及塑性区半径的封闭解,但D-P准则的塑性屈服面为一圆形,对于裂隙、节理较为发育的岩石材料而言,其应用准确性较差。此外,张常光等[14]将围岩划分为弹性区和塑性区,基于统一强度理论,获得了弹脆塑围岩状态的封闭解答,但对于深部巷道而言,其开挖后明显存在一个岩石力学性质较差的破裂区,该区承载能力较弱,是巷道支护的重点[1,3,15]。张强等[10]将围岩依次划分为弹性区、塑性承载区及破裂区,求得了围岩应力及变形的封闭解,但对于高围压状态下的围岩而言,当其由塑性承载区进入破裂区的过程中,其围岩参数(内摩擦角及黏聚力等)逐渐降低,进而引起全应力-应变曲线呈现连续下降的变化特征,而并非瞬时跌落,因此将围岩划分为弹性区、塑性区、软化区及破裂区更为合理。
鉴于此,基于统一强度理论,考虑围岩塑性承载及滞后连续软化特性,建立其应力-应变四阶段变化模型,并推导围岩应力场、位移场及塑性区半径的封闭解析解;同时,将该模型分别与理想弹塑性模型、弹脆塑模型、应变软化模型及塑性承载模型进行对比分析,并开展相关参数对该模型下围岩状态的影响,其研究结果可为高围压下巷道围岩稳定性评价与支护设计提供重要理论依据。
1 力学模型的建立
1.1 四阶段力学模型
图1为某矿不同围压下砂质泥岩全应力-应变曲线,由图可知,该岩石在三轴压缩过程中大约经历了4个阶段:弹性变形阶段、塑性流动阶段、应变软化阶段及残余流动阶段。因此可将围岩视为处于弹性区e、塑性区p、软化区s及破裂区c 4种应力状态,并建立如图2所示的巷道围岩力学模型。巷道开挖初期,围岩基本处于弹性状态,当其最大与最小主应力满足统一强度准则时,开始进入塑性状态,该状态并非无限的扩展,其扩展范围受软化区及破裂区的约束;当塑性区剪应变增量满足一定关系时,围岩开始由塑性状态进入应变软化状态,直到围岩参数达到某一残余值时,开始进入破裂状态,并最终在支护阻力的作用下达到稳定平衡状态[16-17]。开挖巷道特征:巷道开挖半径为a;无穷远处静水应力大小为σ0;支护阻力为pin;塑性区、软化区及破裂区半径分别为Rp、Rs和Rc。此外,Y和Yr分别为等效峰值强度及残余强度;ηi为各区围岩扩容系数,可由塑性势函数来确定;巷道围岩环向、径向应力及应变分别用σθi、σri和εθi、εri来表示。其中,下标“i”表示符号“p”、“s”和“c”,代表围岩3种不同区域。
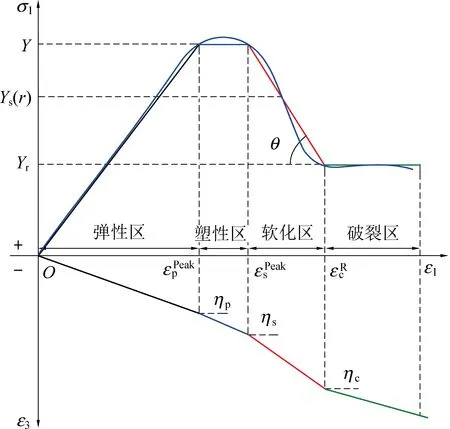
图1 砂质泥岩全应力-应变曲线Fig.1 Stress-strain curve of sandy mudstone
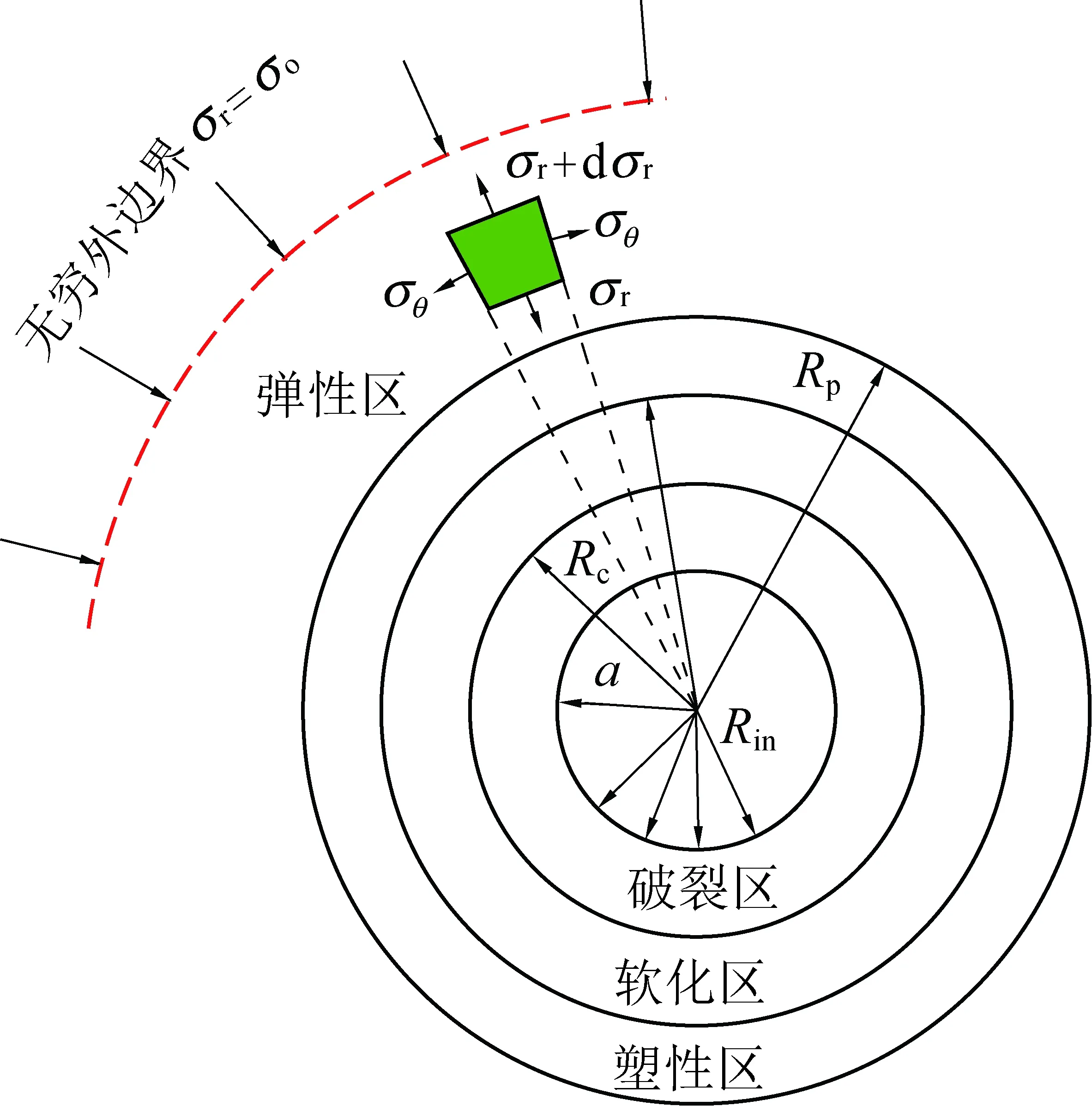
图2 深部巷道围岩力学模型Fig.2 Mechanical model of crack deep roadway
1.2 统一强度准则
统一强度理论(简称UST)是以双剪屈服准则为基础,考虑双剪单元体上全部应力分量和中间主应力对材料屈服失效的影响而建立的[14-15]。该理论适用于多种材料介质,其表达形式也不尽相同。在岩土工程中,常用材料的黏聚力(C)和内摩擦角(φ)来表示,且一般规定压应力为正,拉应力为负,则UST屈服函数可表示[13-14]为:
(1)
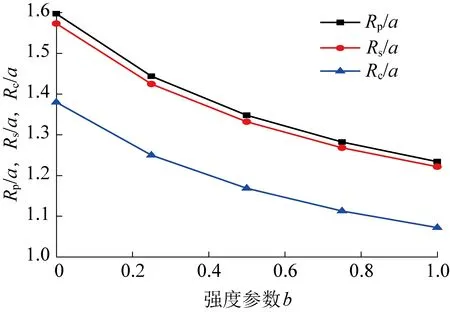
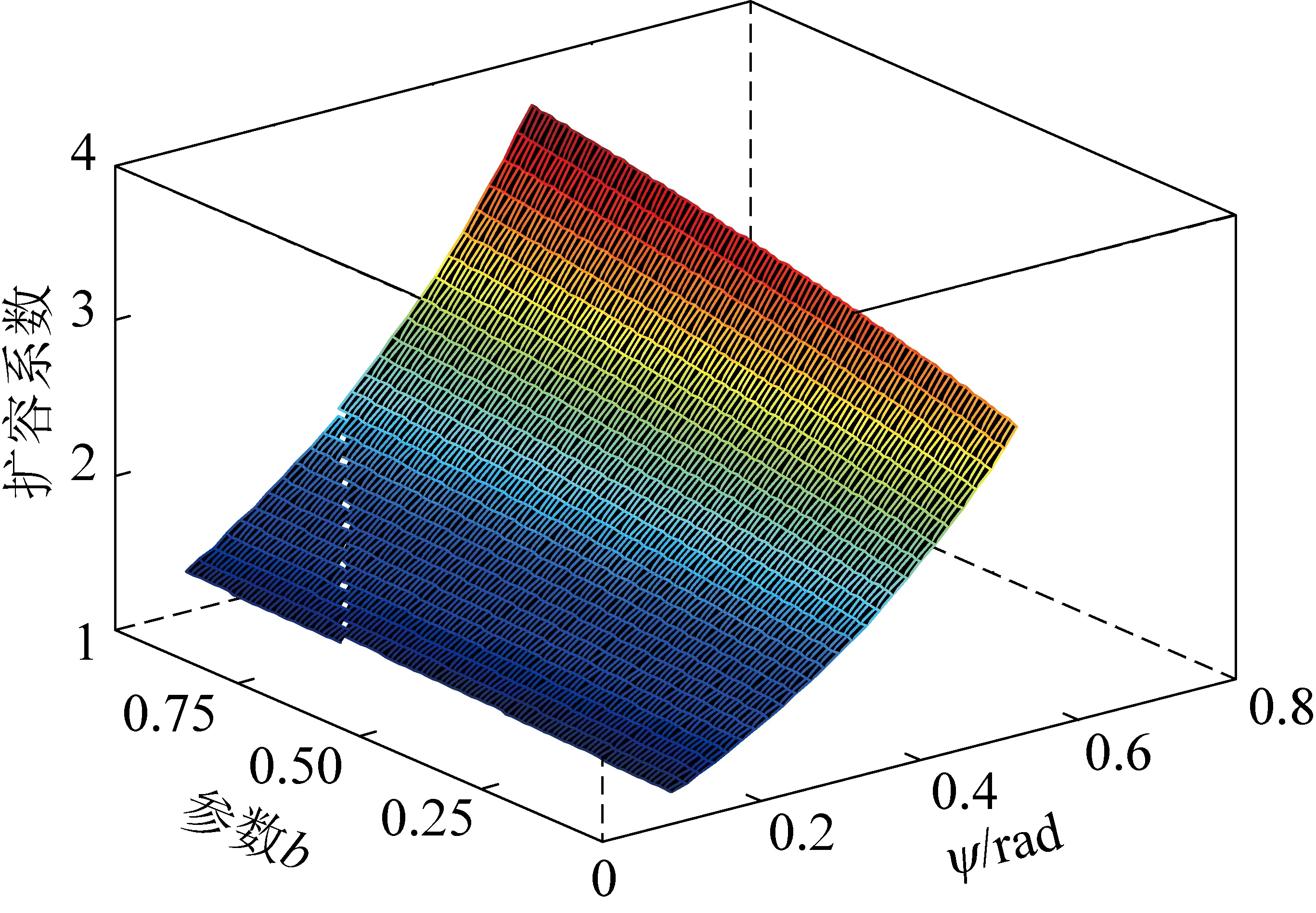
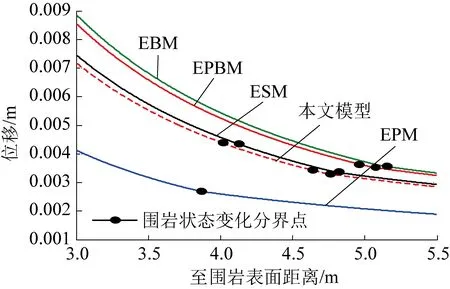
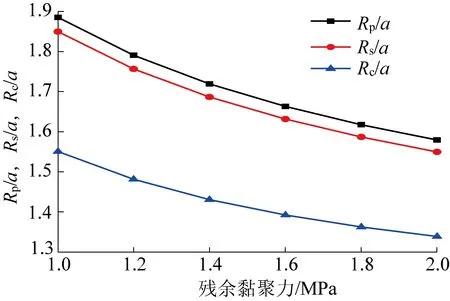
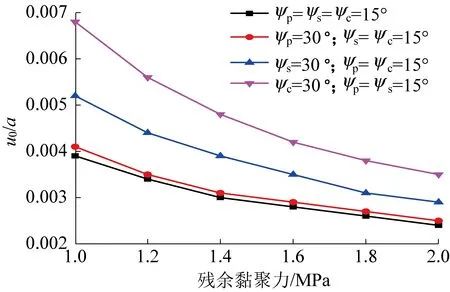
式中:σ1、σ2和σ3分别表示最大、中间和最小主应力,MPa;b为强度参数,反映中间主切应力及其相应面上的正应力对材料屈服破坏的影响程度,且0≤b≤1。当b=0时,UST转化为M-C强度准则;当b=1时,转化为双剪强度准则;当0 在实际工程中,一般可用中间主应力系数σ2来表示3个主应力之间的关系[19]: (2) 式中:对于岩石材料而言,n一般满足条件2ν≤n≤1,当n→1 时,σ2越接近最大和最小主应力平均值;ν为岩石材料泊松比。为简化计算过程取n=1。此时UST可改写为: σ1=Npσ3+Y (3) 对于轴对称平面应变问题,当pin<σ0时,环向和径向应力分别为最大、最小主应力,轴向应力为中间主应力,即σ1=σθ,σ2=σz,σ3=σr,将其代入式(3)中,则可表示为: σθi=Npσri+Yi (4) 岩石塑性变形是非线性的,一般满足非关联流动法则,可由塑性势函数来表示: f(σθi,σri)=σθi-ηiσri (5) (6) (7) (8) 取式(7)和(8)之比,即得峰后各区塑性主应变与扩容系数之间的关系式: (9) 对于轴对称平面应变问题,各区满足的应力平衡方程为: (10) 基于小变形假定,各区满足的几何方程为: (11) 式中:εri和εθi分别为围岩径向和环向应变;uri为径向位移,m。 该模型满足的应力边界条件可概括为: (12) 结合弹性力学理论,易得弹性区应力、应变及位移表达式为: (13) 在r=Rp处,围岩处于弹塑性临界状态,因此其环向和径向应力满足UST准则,故将式(13)代入式(4)中易得σRp表达式为: (14) 塑性区围岩应满足应力平衡方程式(10)及屈服准则式(4),结合边界条件(σre)r=Rp=σRp,即得塑性区应力表达式为: (15) 由式(15)可知,塑性与软化区径向接触应力为: (16) 假定塑性区应变仅有塑性应变组成,则将式(11)代入式(9)中,结合位移边界条件(urp)r=Rp=(ure)r=Rp,可得塑性区位移及应变表达式为: (17) 在软化区,假定岩石强度的衰减仅与黏聚力有关,则软化区的参数Ys(r)应满足关系: (18) 式中:λ为软化系数;εθs(r)为软化区环向应变。 根据塑性区应变求解方法,将式(11)代入式(9),结合径向位移连续条件(urs)r=Rs=(urp)r=Rs,可得软化区应变及径向位移表达式为 (19) (20) 将式(19)和(20)代入式(18),整理后可得: (21) 由式(21)和(4)可得,软化区围岩满足的本构关系为: (22) 将式(22)代入式(10),结合r=Rs处应力接触条件(σrs)r=Rs=σRs,可得软化区应力表达式为: (23) 同塑性区应力求解过程,结合边界条件(σrc)r=a=pin,即得破裂区应力表达式为: (24) 同理,结合位移边界条件(urs)r=Rc=(urc)r=Rc,可得残余区应变及径向位移表达式为: (25) 理论上来讲,只要满足所有的边界及接触条件,其所得围岩应力与变形状态就是正确的[1]。由以上各式可知,要想获得围岩状态的封闭解,首先要确定塑性区、软化区及破裂区半径的大小。在r=Rc处破裂区与软化区径向应力满足条件(σrs)r=Rc=(σrc)r=Rc,联立式(23)和(24),可得Rp、Rs和Rc满足的关系式之一为: (26) 一般情况下,在高围压条件下塑性区的扩展是有限的,将受到软化区与破裂区的限制与约束[1,10],可用塑性区剪应变增量Δγ*来表示塑性区的扩展情况。当Δγ*达到某一值时,可认为围岩开始由塑性阶段进入软化阶段,此时Δγ*可表示为: (27) 由式(17)代入式(27)中可得,塑性区与软化区半径之间的关系为: (28) 在软化区,其应变软化系数λ可由直线BC的斜率来确定,表达式为: (29) 将式(28)代入式(29)整理后可得: (30) 将式(28)和式(30)分别代入式(26)中,整理后可得破裂区半径表达式为: (31) 将式(31)依次代入式(30)和(28)即得Rs和Rp的具体表达式。 以文献[1]所示工程背景为例,唐口矿运输石门等效开挖半径a=3.0 m,埋深1 028 m,垂直应力与水平应力分别为23.77、23.04 MPa,故取原岩应力σ0=23.4 MPa。室内三轴压缩试验测得岩石力学参数为:弹性模量E=30.0 GPa、泊松比ν=0.25、初始内摩擦角φ=30°,初始与残余黏聚力分别为5.85 MPa和2.0 MPa。此外,三区初始剪胀角均为ψp=ψs=ψc=15°,应变软化系数λ=37.5 GPa,塑性区剪应变增量Δγ*=0.000 1。为有效反映强度参数、扩容系数及模型选取对围岩状态变化的影响,现采用控制变量法对其逐一进行分析。 由图3可知,强度参数b的选取将对围岩状态变化产生重要影响。随着b的不断增加,围岩环向应力均表现出先增大后减小的变化特征,且在弹塑性交界处达到最大值;且当b由0变化至1.0过程中(即M-C准则向双剪强度准则过渡),围岩环向和径向最大应力均呈现出逐渐增大的变化特征。围岩环向应变与径向应变均随b的增加逐渐减小,但径向应变沿围岩表面至深部却呈现间断不连续分布特征,这主要与前文假设条件相关(弹塑交界处径向位移相等,由式(11)可知该部位环向应变也相等,但径向应变不一定相等)。对于破裂区范围而言,随着b的不断增加,其破裂区范围却不断减小,这主要是因为当b=0时没有考虑中间主应力对围岩状态变化的影响,易较高估计围岩破裂范围,此时造成锚杆索支护长度设计与实际工程偏差较大,故而产生支护失效或成本较高的现象[20]。 图3 不同强度理论参数的围岩应力、应变分布Fig.3 Stress and strain distribution curve of different strength parameters 图4表明强度参数的选取对围岩峰后各区破坏范围均产生重要影响,随着b的不断增加,Rθ、Rs和Rc均不同程度减小,且减小速率却不断降低。例如,当b由0变化至0.5时,Rθ/a、Rs/a及Rc/a分别减小了0.249、0.241和0.211,降低了15.59%、15.32%和15.29%;而当b由0.5变化至1.0时,Rθ/a、Rs/a及Rc/a仅分别减小了0.114、0.111和0.097,降低了8.46%、8.33%和8.30%。以上数据表明较其他准则而言,选取M-C准则,易较大预估围岩峰后破坏范围,提高支护参数(长度、强度)设计安全性,但也易造成支护成本偏高、支护强度浪费的现象,因此建议尽量选取中间强度参数来预估围岩峰后破坏情况。 图4 不同强度参数的围岩峰后破坏范围分布Fig.4 Range of post failure distribution of different strength parameters 由图5可知,ηi的取值与强度参数b和剪胀角ψi密切相关,且ηi与参数b和ψi均成正相关关系。例如当b=0,ψi由5°变化至10°~20°的过程中,ηi由1.191增加至1.420~2.040,提高了19.23%~71.28%;当ψi=15°,b由0变化至0.5~1.0过程中,ηi由1.700增加至1.838~1.931,提高8.12%~13.59%。以上数据表明:①对于剪胀性较强的岩石更容易产生扩容现象,加剧围岩失稳;②当由M-C准则向双剪强度准则过渡过程中(b由0趋向于1.0),岩石扩容效应更加显著,围岩失稳倾向性也相对加剧。 图5 剪胀角和强度参数对扩容系数的影响Fig.5 Influence of dialtancy angle and strength parameter on dilation coefficient 由图6可知,模型的选取对围岩峰后破坏区位移具有显著影响。当选取不同的模型时,其围岩峰后破坏区位移呈现出EBM>EPBM>ESM>本文模型>EPM的变化特征,且EBM与EPBM、ESM与本文模型两两之间所得结果较为接近,且前者大于后者,也就是说对于易发生脆性破坏的围岩而言,较应变软化围岩,更易产生较大变形。 图6 不同模型下围岩变形分布情况Fig.6 Displacement distribution of surrounding rock with different models 由图7和图8可知,残余黏聚力对围岩峰后破坏区范围及表面位移均产生重要的影响。随着残余黏聚力的不断增加,围岩峰后破坏范围及表面位移呈现出非线性减小的变化特征。例如,当cr由1.0 MPa变化至1.6~2.0 MPa,其Rθ/a、Rs/a及Rc/a分别减小了0.222~0.305、0.217~0.300和0.159~0.212,降低了11.78%~16.18%、11.74%~16.22%和10.25%~13.67%,表面位移u0/a减小了1~11.5 mm,降低了28.21%~38.46%。此外,由图8也可以看出,随着峰后破坏区ψi的不断增加,其围岩表面位移也不同程度增大,且破裂区剪胀角对其影响最为显著,软化区剪胀角次之,塑性区剪胀角影响最小。这主要是因为ψi越大,ηi也就越大,其围岩体积膨胀程度也就越大,为有效释放围岩变形能,围岩整体变形加剧。 图7 残余黏聚力对围岩峰后破坏范围的影响Fig.7 Influence of residual cohesive force on post peak failure range of surrounding rock 图8 残余黏聚力对围岩表面位移的影响Fig.8 Influence of residual cohesive force on surface displacement of surrounding rock 1)建立了深部圆形巷道围岩弹性区-塑性区-软化区-破裂区四阶段应力-应变模型,基于UST准则和非关联流动法则,考虑中间主应力及扩容系数的影响,求得围岩应力、应变及变形的封闭解析解。 2)强度参数对围岩状态变化具有重要影响,随着强度参数的不断增加,围岩环向应力峰值及峰后破坏范围均不同程度增大,应力曲线左移;随着剪胀角的不断增加,其围岩表面位移不同程度增大,且破裂区剪胀角对其影响最为显著,软化区次之,塑性区影响最小。 3)随着残余黏聚力的不断增加,围岩峰后破坏范围及表面位移均呈现出非线性减小特征,其减小速率不断降低;与其他应力-应变模型相比,其围岩峰后破坏区位移呈现EBM>EPBM>ESM>本文模型>EPM的变化特征;此外,基于塑性势理论建立扩容系数与强度参数和剪胀角之间的关系,可有效避免关联流动法则较为保守的不足。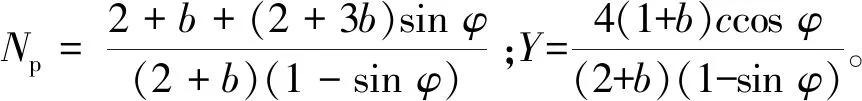
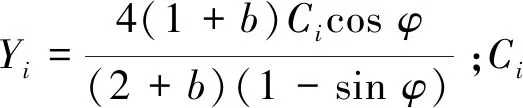
1.3 扩容系数定义
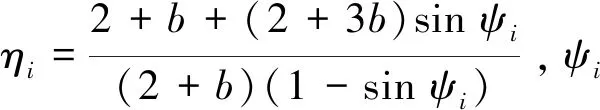
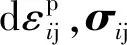
2 模型的求解
2.1 基本方程
2.2 弹性区应力、应变及位移解答
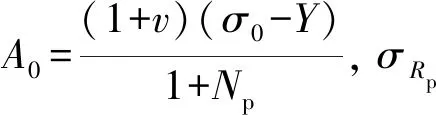
2.3 塑性区应力、应变及位移解答
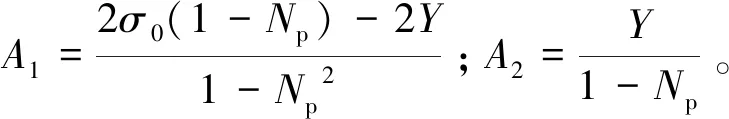
2.4 软化区应力、应变及位移解答
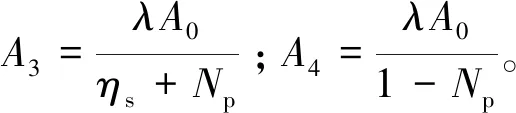
2.5 破裂区应力、应变及位移解答
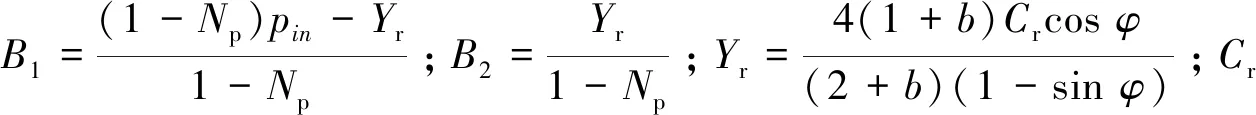
2.6 各区半径的求解
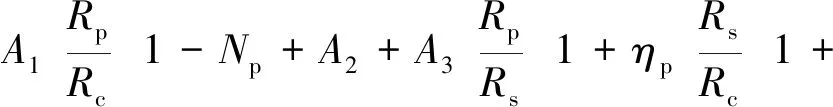
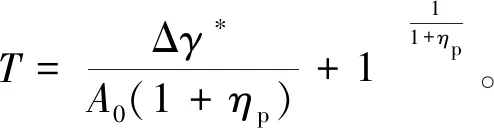
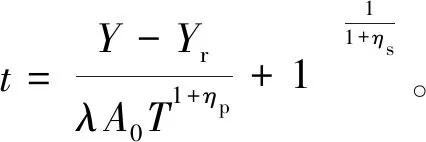
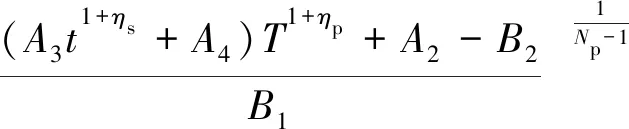
3 案例分析
3.1 工程条件
3.2 强度参数对围岩应力、应变状态的影响
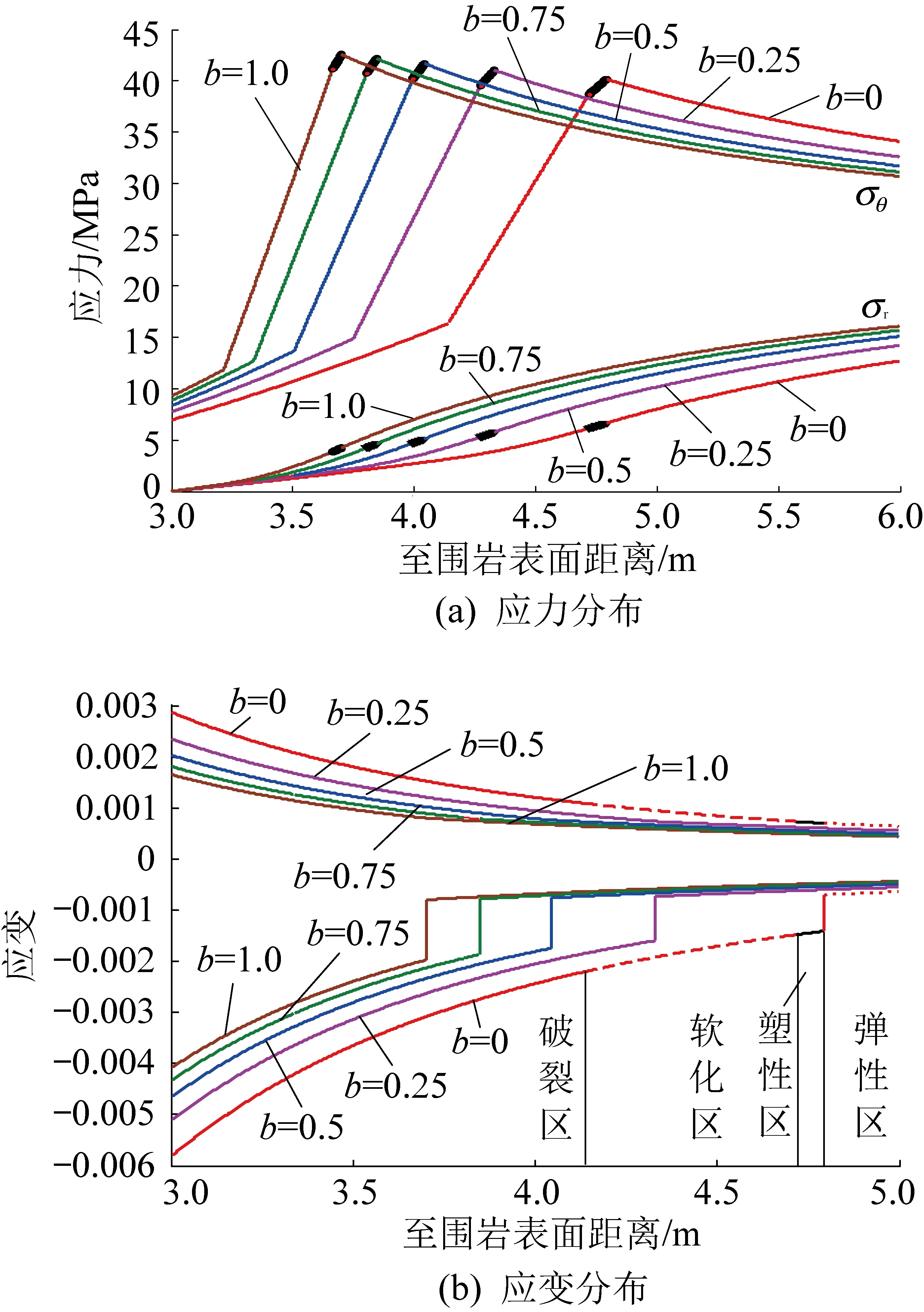
3.3 强度参数对围岩峰后破坏范围的影响
3.4 强度参数对扩容系数的影响
3.5 模型选取对围岩变形的影响
3.6 残余黏聚力对围岩峰后范围的影响
4 结 论
