多维异构网络数据智能预加密云推送方法研究
2022-07-20王志刚王辰阳李恒武
王志刚,王辰阳,李恒武
(中国人民解放军战略支援部队信息工程大学,河南 郑州 450001)
1 引言
互联网中数量众多的多维异构数据被汇集在一起,形成了全球规模的信息共享环境。为贴合用户实际搜索需要,需要推送的数据呈现出多样化的趋势。在保障数据安全性的同时,为用户提供可靠的信息推送服务,是目前通信领域研究的重要目标。
针对信息推送相关问题,周长敏等以旅游信息为例,提出一种旅游信息适应性自组织推送方法。通过求解目标使用者及其他使用者间的相似度,探寻目标使用者的最近邻集合。采用模糊遗传算法明确加权函数,计算目标使用者对某旅游项目兴趣度预测值,把预测值最高的旅游项目推送给使用者。但该方法耗时较长,且数据推送存在偏差情况。张雪峰等构建一种参与者胜任度和接受度的任务推送模型。在模型中提出识别潜在参与者的思路和过程,运用启发式相似度算法分析任务相似度,描述并量化参与者表现。确保参与者回复率,降低多次推送。但该方法推送应用范围存在一定局限性。
为进一步完善数据推送性能,提出多维异构网络数据智能预加密云推送方法。通过分析多维异构网络数据特征,划分同构与异构数据。并在确保推送数据隐私前提下,创建云推送平台,解决多维异构网络数据推送问题,实时为用户推送最新信息。
2 多维异构网络数据智能预加密云推送
2.1 多维异构网络数据特征分析
对异构数据的分析不足,致使在推送过程中的速率较低。因此运用分布于不同云服务器内的云数据获取数据主成分,并把各个关键数据成分值X
和给予的μ
值相减,就能明确该成分在方向内的偏移值,将异构数据的关键数据成分值X
引入矩阵S
,得到S
=[X
,X
,…,X
](1)
把矩阵S
与其转置矩阵S
相乘,计算求解数值的均值大小。将均值记作数据的全局异构水准,具体表示为
(2)
式(1)中,μ
代表按照评估得到的权重值,N
是样本总数,因为V
是已知值,所以此数据样本的异构水准可使用特征值V
进行描述。若出现多维异构数据需要推送,此时每个数据的主成分不能划分成X
-X
,需要将X
转变成X
,因此矩阵S
变化为
(3)


(4)
在云数据中,即便拥有大量的多维异构数据,但还存在一定数量的同构数据。在用户需要推送内容是同构数据情况下,采用协方差矩阵根据其数据特征进行矢量分解,分解同构数据就可得到更加高效的推送模式,无需在每个点采取重复迭代,节约数据通信时间。


(5)

(6)
因此在每个云数据样本足够的状态下,推算同构数据的精确度较高。因为同构数据的自身属性问题,将此增量更新解析式记作

(7)

(8)
在以上计算过程中能够得出,协方差矩阵具备一定对称性,在进行云推送时,同构数据每次更新仅需要传输半个协方差矩阵即可,减少了数据传输数量。假如网络系统个数是M
,参数数量是d
,同构数据计算过程的时间复杂度是O
(M
,d
)=(M
-1)(d
(d
+1)/
lgd
)(9)
多维异构数据是对同构数据关键成分采取拓展的一种形式。为了便于数学运算,加入置换矩阵P
,对云服务器内得到的样本实施置换映射,将计算结果表示成y
y
=(y
,y
)=P
X
(10)
式(10)目的是为了把目前样本内和同构数据内相等的部分集合在矢量前面,记作y
,把不同部分安放于矢量后面,记作y
。同理,将均值矩阵与协方差矩阵采取置换,计算结果依次为μ
=(μ
,μ
)=P
μ
(11)

(12)
μ
与置换矩阵均为上次计算得到的数值,σ
表示m
样本内已经获得的协方差矩阵,σ
表示和同构数据内不同因子的协方差矩阵,σ
表示两者之间协方差组成的矩阵。上述解析式均满足高维分布特性,因此云数据样本能够使用高维分布进行推算,具体描述为
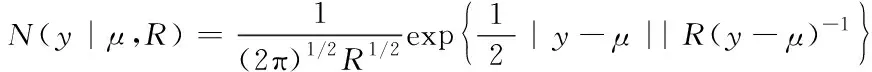
(13)
由此,将信息云更新后推送异构数据的解析式定义为
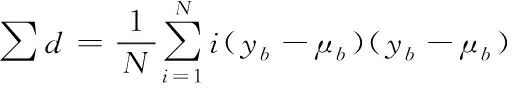
(14)
因为在异构数据内,各种云数据的因子数量是互不相等的,所以需要探寻每个N
的具体数值。因为转置矩阵可以减少数据传输数量,继而把传输复杂度记作O
(M
,d
)=(M
-1)(d
+2d
)(15)
通过上述过程,能够完成迅速分离数据源内的同构数据和异构数据,为后续数据智能预加密效率与云推送方法的有效完成提供帮助。
2.2 数据智能预加密计算
预加密可以保护数据隐私,是提高云推送服务安全性能的一项关键措施,但数据加密后会损失多种特征,让云服务器对密文的处理有相当困难。由此,使用全同态加密算法完成加法同态与乘法同态,让云服务器不必接触明文数据就可以便利地处理推送数据。
E
(m
⊕m
)=E
(m
)⊗E
(m
)(16)
同态,就是一个加密方案E
符合式(16)的约束条件的计算过程。式(16)中,m
、m
表示明文消息,E
表示加密函数,⊗是密文的某类计算形式,⊕是对明文进行计算的某种形式。在实施数据智能预加密时,首先要使用全同态加密算法对明文进行加密。然后把密文数据输送至云端,在传送数据处理请求时,云端服务器不用对密文解密就能实现对应操作。全同态加密流程共包含三个步骤:对明文数据采取二进制分组,分组长度按照安全请求进行自定义操控;对各明文分块进行加密,获得相对应的密文分块;把全部密文分块融合为完整的密文数据C
。加密详细过程为:挑选加密参变量P
、Q
、R
,P
为正奇数,Q
为正整数。P
、Q
值在密钥生成阶段进行确认,P
为加密密钥,R
为加密过程中挑选的随机数值;把消息M
分组成多个长度是L
的消息分块;分别读取明文分块内的字符,同时将其变换成二进制数字;采用加密算法对二进制数字实施加密操作,具体如式(17)所示。并将多个密文分块整合为完整的密文数据。
c
=m
+2R
+PQ
(17)
按照全同态加密算法性质,依次对此算法的加法同态与乘法同态性实行验证。如果有两组明文m
、m
,加密之后的密文依次是c
、c
,继而得到c
=m
+2R
+PQ
(18)
c
=m
+2R
+PQ
(19)
对密文c
、c
采取加法操作c
+c
=(m
+m
)+2(R
+R
)+P
(Q
+Q
)(20)
将 cmod
p
的值当作噪声,若噪声m
+2R
<P/
2的情况下,得到(c
+c
)modp
=(m
+m
)+2(R
+R
)(21)
将(m
+m
)+2(R
+R
)进行对2取模m
+m
=[(m
+m
)+2(R
+R
)]mod 2(22)
由式(22)中可知,本文算法符合加法同态性。同理,对密文c
、c
实施乘法操作c
×c
=m
m
+2(2R
R
+m
R
+m
R
)+P
[PQ
Q
+Q
(m
+2R
)+Q
(m
+2R
)](23)
因为
m
m
+2(2R
R
+m
R
+m
R
)<P
(24)
所以,对P
与2依次取模得到m
m
=[(c
×c
)modp
]mod 2(25)
至此可知,本文数据智能预加密算法符合乘法同态性,可以实现数据智能预加密。
2.3 基于对数优化的云推送平台设计
在对数据智能预加密后,设计云推送平台。云推送表示处于云计算大环境下,客户端接收经过服务端主动输送消息的技术,让用户无需主动检查更新,为用户提供更多的便利服务。与此同时,云服务器端会使用云推送平台把每个系统内的多维异构数据推送至用户。本文云推送方法关键有如下几个方面:
云数据层作为全局云推送平台最重要的部分,云数据是通过每个系统内的多维异构数据组成的,全部数据都属于云数据层,并让云数据层更好地完成数据逻辑虚拟化目标;数据管理层为云推送平台逻辑框架的中心,是实现云推送过程中数据和推送同步进行的关键工作层;在应用接口层中,用户能够利用订阅不同的应用板块对应用接口层进行自动配置,得到不同的数据储存、访问的应用服务;访问层中,授权用户能使用对应接口完成系统数据访问,并按照用户访问权限不同,每种用户访问的形式也各不相等;用户层担负对每个用户的注册信息进行整合,并且也能管理各类型的登录终端,例如IOS
、PC
等。具体平台架构如图1所示。
图1 云推送平台架构图
若处在随机时间单元T
中,单个用户订购业务个数是α
(T
),那么n
个用户的订购业务总数是n
α
(T
),已知α
(T
)满足泊松分布,均值参数是λ
,把现阶段用户i
在信道内存留的数据积压描述成Q
(T
),信道状态是r
(T
),那么用户集群信道状态集合是r
(T
)=(r
(T
),r
(T
),…,r
(T
))(26)
在得到信道状态后,能够准确推算用户的信道输送速度u
(T
)。假如全部T
单元中用户i
的传输时间间隔总数是w
(T
),得到用户的全信道速度u
(T
)=w
(T
)μ
(T
)τ
(27)
所以,将信道内单个用户的服务速度集记作
u
(T
)=(u
(T
),u
(T
),…,u
(T
))(28)
总结上述步骤,获得信道内的动态数据积压总数是
Q
(T
+1)=max[Q
(T
)-u
(T
),0]+n
α
(T
)(29)
评估云推送平台稳定性条件为

(30)
如果T
时段中用户信道数据传输功率是ρ
(T
),把用户数据能耗与所有用户的能耗总量分别描述为E
(T
)=ρ
(T
)w
(T
)τ
(31)
在式(31)前提下计算基于推送策略的李雅普诺夫函数公式

(32)
为了判断单元时间中函数的详细变化情况,本文创建一种新的函数表达式
Δ(T
)=E
{ln(L
(T
+1)-L
(T
))|Q
(T
)}(33)
式(33)的函数表达式关键对李雅普诺夫函数的优化进行对数计算,即为降低信道自身传输噪声的干扰作用,减少噪声敏锐性。关于时间单元T
,把李雅普诺夫函数的乘法函数记作VE
{E
(T
)|Q
(T
)}。在获取最低能耗值状况下,把现阶段最优业务个数描述成式(34)。

(34)
在确保数据安全同时,有效解决多维异构网络数据跨平台推送问题,快捷高效地为用户推送最新信息。
3 仿真与分析
在本节中,展示了实验环境和性能指标,并对实验结果进行了主要分析。
3.1 实验环境
此次仿真使用EXE文件修改器与OpenStack软件模拟构建私有推送平台。设置该平台5个物理节点,并通过100Mbps局域网重新连接。实验数据来自明尼苏达大学相关的研究小组公布的真实数据集MovieLens,每个物理节点均配备了Intel(R) Pentium(R) CPU G4400 @ 3.30GHz,8GB RAM,64位中文版操作系统。测试的客户端型号为Xiaomi mix3,内存6GB,晓龙845 CPU。仿真内,设定数据传输速分布是450kbit/s的负指数分布,最高传输速率是1100kbit。
为了验证所提方法可靠性,将通信率及推送留存率当作云推送方法评估的三项指标,对所提方法与云计算环境下旅游信息适应性自组织推送算法(文献[4])、众包模式下基于参与者胜任度和接受度的任务推送模型(文献[5])方法进行仿真对比。
3.2 通信率对比实验
通信率表示单位时间内,用户和云推送的通信次数,检验用户是否愿意采用该方法实施数据推送,同时检测通信数量较多时能否发生不可估计的复杂问题。通信率越低说明数据云推送过程所花费的通信量越少,推送效果越好。基于上述实验环境,计算三种方法的通信率,得到仿真结果如图2所示。

图2 通信率对比示意图
从图2中可知,两种文献推送方法下的通信率基本维持不变,这是因为在推送任务队列消息过程中,会持续向服务器发送请求。而所提方法一直保持信息收集状态,伴随系统运行,任务量增加,通信率最低为1.55%。因为所提方法利用了协方差矩阵根据数据特征,对数据源内的同构、异构数据进行了快速分类,使得后续推送稳定性能较优,即任务数量越多,耗费的通信量越低。
3.3 留存率对比实验
留存率表示固定时段中,用户保存此推送消息的比率,可以体现推送方法对用户的影响程度。实验以1~8周的信息留存时间作为实验周期,得出三种方法下的推送留存率如图3所示。

图3 推送留存率对比图
图3仿真结果表明,所提方法通过预加密方式维护了云推送服务安全,因此每个星期的留存率均高于文献[4]、文献[5]方法,8个星期后两种文献方法的留存率已经低于32%,而所提方法的留存率高达58%,说明所提出的推送方法较符合用户实际需要,推送的消息更可靠,安全性较高。
4 结论
针对多维异构网络数据推送效率不高等问题,提出一种基于对数优化的数据智能预加密云推送方法。运用智能预加密手段实现多维异构网络的安全推送,仿真结果证明,该方法可以为用户提供及时有效信息推送服务。但该方法能否符合全部用户需求,还要进行具体验证,云推送自身性能的提高与演化也是接下来研究的关键内容。
