星型倾斜壁节点蜂窝结构的动态力学特性

刘崎崎，胡 俊

(安徽建筑大学 土木工程学院，安徽 合肥 230601)

蜂窝材料是一种由形成孔穴的棱边和壁面固体板所构成的相互联结的网络体，具有质量轻、能减震缓冲等多种特性，是海内外学者广泛关注的对象。多孔材料的性能依赖于孔穴的形状和结构。最早在1987年，Lakes就提出若各向同性的拉胀材料[1](也叫负泊松比材料)在X方向压缩，则Y方向拉胀材料发生两侧颈缩，其主要的变形结构为内凹结构、旋转结构。Hu等[2]系统地分析了内凹六边形结构的几何参数对具有负泊松比效应的蜂窝结构平台应力的影响。沈振峰等[3]将凹角倾斜壁替换成为内凹环形壁，产生了一种新的具有拉胀效应的蜂窝模型。韩会龙等[4-5]为验证负泊松比蜂窝材料的动力学性能也受到胞元空间拓扑参数的影响，对星形节点蜂窝结构中几何参数因子改变时的变形模式、能量吸收展开深入研究。Wang等[6]提出将内凹胞元和星型蜂窝结合起来组成新的内凹胞元，并采用数值分析方法研究了负泊松比效应的材料在冲击碰撞作用下的动力学性能和吸能特性。Qiao等[7]分析了匀称和阶梯型的双箭头蜂窝的准静态行为和碰撞行为，结果表明拉胀效应会导致模型横向颈缩，并显著影响静态平台应力。

由此可见，蜂窝材料的性能不仅由基体材料的特性决定，也由胞元几何拓扑结构决定，良好的拓扑能够得到理想的蜂窝结构。根据实际工程需求，实现蜂窝材料结构的自主研发，建立胞元微拓扑结构与力学性能之间的关系，是许多科学研究人员想要突破的课题。另一方面，胞元结构的几何参数，如胞壁长度、胞壁厚度和节点夹角，也影响着结构材料的力学性能，如何建立胞元拓扑几何参数与材料间的动力学响应之间的关系，也是一个重要课题。本文将星型蜂窝和倾斜壁连接，改变星型节点夹角和冲击速度，探究在相同速度不同节点夹角和相同节点夹角不同速度下星型倾斜壁节点蜂窝结构的力学特性，并给出细致的解释，以丰富星形蜂窝结构的基础理论。

1 计算模型

1.1 有限元模型建立

面内冲击荷载下的计算模型如图1所示。其胞元是星型结构，相邻胞元使用双倾斜壁韧带连接。如图1(a)所示，胞壁长度(L)与倾斜壁长度(LS)均为2 mm，胞壁厚度(t)为0.2 mm，胞壁厚度是边长的1/10。

(a) 星型倾斜壁微单元 (b) 模型局部二维图 (c) 试件荷载冲击示意图

本文主要探究负泊松比蜂窝结构在改变节点夹角(β)时，不同冲击速度(v)下的冲击动力学性能。星型倾斜壁蜂窝材料的尺寸参数见表1。面外长度为1 mm，基体材料为金属铝，弹性模量Es=69 GPa，密度ρ=2700 kg/m3，泊松比υ=0.3，屈服应力σys=76 MPa。刚性板密度ρ=7800 kg/m3，弹性模量Es=210 GPa。假定本模型是理想弹性塑性模型，并服从Mises屈服准则。采用ANSYS/LSDYNA显示动力分析软件进行数值模拟，计算时使用四节点四边形的SHELL163壳单元进行网格划分，每条棱边单元数设置的单位长度是0.5 mm。参考文献[4]，试件尺寸X轴正方向建立13个微单元，Y方向上建立15个微单元。为防止计算产生初始穿透，选择通用接触和自动接触，摩擦因数为0.02。边界条件定义与文献[3-6]完全相同。

表1 星型倾斜壁蜂窝材料的尺寸参数

1.2 相对密度

相对密度是影响蜂窝材料性能的最主要因素。含有显微参数的模型在实际工程中使用时很复杂，需要建立微单元几何数据同密度联系起来的关系式以方便工程师使用。相对密度(Δρ)是蜂窝结构微单元固体面积(AS)与蜂窝结构微单元总横截面面积(Atotal)的比值，即：

(1)

1.3 有限元模型的验证

为验证有限元模型的合理性，建立与文献[4]一样的模型。冲击速度为20 m/s时，有限元模型沿Y轴方向压缩的面内变形模式如图2所示。

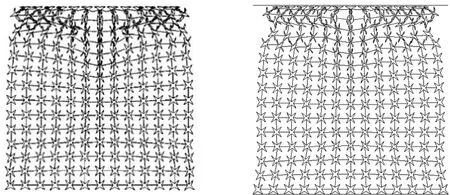
(a) ε=0.174

从图2可以看出，两者的压缩变形基本相似，验证了该有限元模型的可靠性。本文均采用同种方法来建立有限元模型，对星型倾斜壁节点蜂窝结构的力学特性进行研究。

2 结果与讨论

2.1 变形模式

2.1.1不同冲击速度的变形模式

v=7 m/s时蜂窝结构的变形模式如图3所示。从图3中可观察到，星型胞元发生轻微旋转并形成塑性铰，倾斜壁连接的菱形成为图形中主要形状，并且在中下部有向内颈缩的趋势。随着形变量逐渐增大，颈缩趋势更加明显，且靠近冲击板一端试件产生膨胀形式，最后蜂窝试件在中间颈缩段产生致密直到模型压溃。

(a) ε=0.12 (b) ε=0.20 (c) ε=0.44 (d) ε=0.60

v=30 m/s时蜂窝结构的变形模式如图4所示。从图4中可明显看到，试件上部两侧的星型胞元向试件中间旋转，并在下端1/3处呈现出正“V”型剪切变形带。随着冲击时间增加，下端两侧星型胞元向外侧旋转，使试件下端的胞元形成倒“V”型剪切变形带，整体图形构成“X”型剪切变形带。和低速冲击时一样，最终试件呈现出中部颈缩和上部拉胀现象，在冲击端和固定端层层折叠逐渐压溃。

(a) ε=0.12 (b) ε=0.20 (c) ε=0.44 (d) ε=0.60

v=70 m/s时蜂窝结构的变形模式如图5所示。从图5可以看出，冲击变形持续时间很短，试件中部和下部胞元变形不明显。随着变形量增加，在惯性作用起主导作用下试件产生层层折叠的现象，直至被压溃。

(a) ε=0.12 (b) ε=0.20 (c) ε=0.44 (d) ε=0.60

分析3种冲击速度下蜂窝结构的变形模式可知，在低速模式和中速模式下，蜂窝结构均产生了明显的中部颈缩和上部拉胀现象。随着冲击速度增加，颈缩现象减弱。在高速冲击模式时，蜂窝结构在惯性效应的引导下在冲击端进行层层折叠并逐渐压溃。

2.1.2不同节点夹角的变形模式

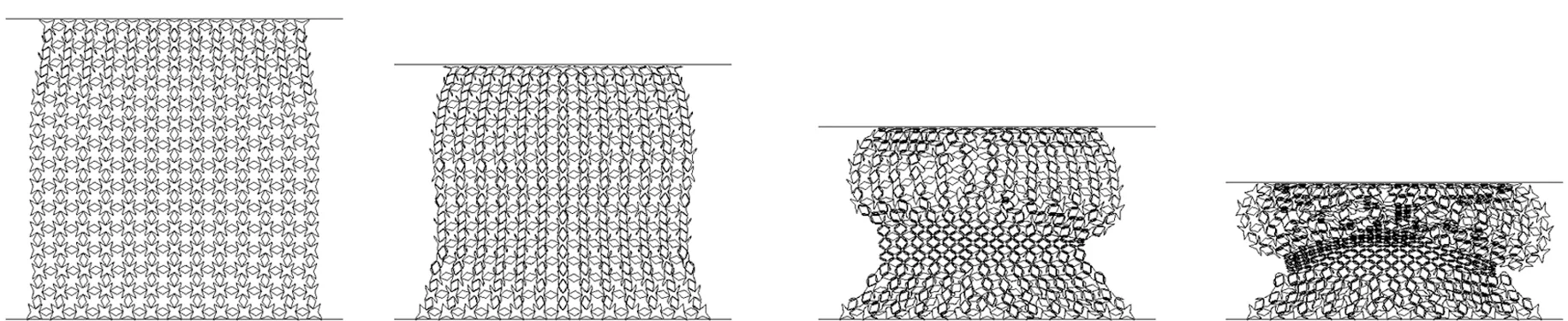
保证蜂窝结构的壁厚和边长不变，在v=10 m/s,ε= 0.30时，不同节点夹角下蜂窝结构的压缩变形如图6所示。由图6可知，蜂窝结构的上端与冲击端是不固定的。在压缩过程中，β=30°或β=45°时，试件上端出现大幅度收缩，随着β增大，收缩减少。此外，β越小，试件中的微单元产生的均匀性压缩变形和颈缩现象越明显；随着β逐渐增加，蜂窝模型的颈缩现象逐渐转变为拉胀现象。由于倾斜壁形成的菱形不易破坏，变形模式为“> <”型剪切变形带逐渐转变为倒“V”型剪切变形带。因此，冲击速度和节点夹角都是影响蜂窝结构变形的重要因素。

(a) β=30° (b) β=45° (c) β=60° (d) β=75°

2.2 应力-应变曲线

大量的研究结果表明，弹性材料、金属材料及弹塑性材料压缩时应力-应变曲线具有广泛的相似性[8]。刚开始压缩时，胞元壁发生弯曲，曲线表现为线弹性阶段，接着曲线波动持续在相对不变的平台，达到临界应力时，孔穴逐渐坍塌并形成塑性铰；最后达到应变最大值，孔穴彻底破坏，相邻胞元壁相互触碰，曲线近乎直线上升，表明试件达到密实状态。在应力-应变图中，曲线与X轴上方围成的面积数值与模型冲击碰撞时吸收能量的数值相同。

2.2.1不同冲击速度下的应力-应变曲线

当β=45°时，不同冲击速度下蜂窝结构的应力-应变曲线如图7所示。由图7可知，应力-应变曲线存在双平台区，在经历第1段平台应力期后，出现应力集体上升的趋势，达到第2平台应力区。引起应力应变特性改变的原因是胞元两侧向中间发生旋转，形成类似于菱形的新胞体结构，产生另一个应力平衡。当v=40 m/s时，其阶段特征明显。此外，随着冲击速度增加，惯性作用起主导作用，平台应力和平台区长度也随之增大。

图7 不同冲击速度下蜂窝结构的应力-应变曲线

2.2.2不同节点夹角下的应力-应变曲线

当v=10 m/s时，不同节点夹角下蜂窝结构的应力-应变曲线如图8所示。由图8可知，在低速模式下，4条曲线均出现双平台应力区，β=45°和60°时的曲线变化趋向非常相似。随着节点夹角增加，试件的峰值应力和平台应力数值相应降低，平台应力区长度增加。当β=45°时，蜂窝结构既有较高的平台应力也有相对较长的平台应力区，可选择此角度进行使用。

图8 不同节点夹角下蜂窝结构的应力-应变曲线

2.3 平台应力特性

蜂窝材料面内压缩的名义应力定义为冲击端的接触反力(F)与模型上端的横截面积(A)的比值，名义应变定义为蜂窝材料上端刚性板向下移动位移(δ)与试件高度(L1)的比值[9]。基于一维冲击波理论，Qiu等[10]在Ruan等[11]的基础上推导出含有拟合系数A和B的平台应力的具有普遍性的经验公式，即：

(2)

基于式(2)，结合最小二乘法拟合曲线，得出蜂窝模型的平台应力公式的基本形式：

(3)

平台应力的计算值与理论值对比如图9所示。基于式(2)和式(3)，图9给出了在不同节点夹角和不同冲击速度下有限元模拟数值与公式(3)的曲线图。当计算模型中低速冲击碰撞时，出现2个平台应力，将2个平台应力值的平均数作为该结构的最终平台应力值。从图9中容易看出，当v>20 m/s时，数值模拟的结果与经验公式相符合，即冲击端平台应力与冲击速度的二次方成正比。而β=30°的星型倾斜壁蜂窝结构的固定端平台应力从1.30 MPa(v=10 m/s)增至1.68 MPa(v=20 m/s)。当β=45°，60°和75°，v=10，20 m/s时，支撑端的平台应力呈现持平趋势。在冲击速度不变的情况下，上端刚性板的平台应力值随着β减小而增大；当节点夹角不变时，随着冲击碰撞速度不断增大，对应的平台应力值也在不断地增加。试件的平台应力随着冲击碰撞速度的增大而逐渐增大。这表明，平台应力大小与节点夹角和冲击速度有关。

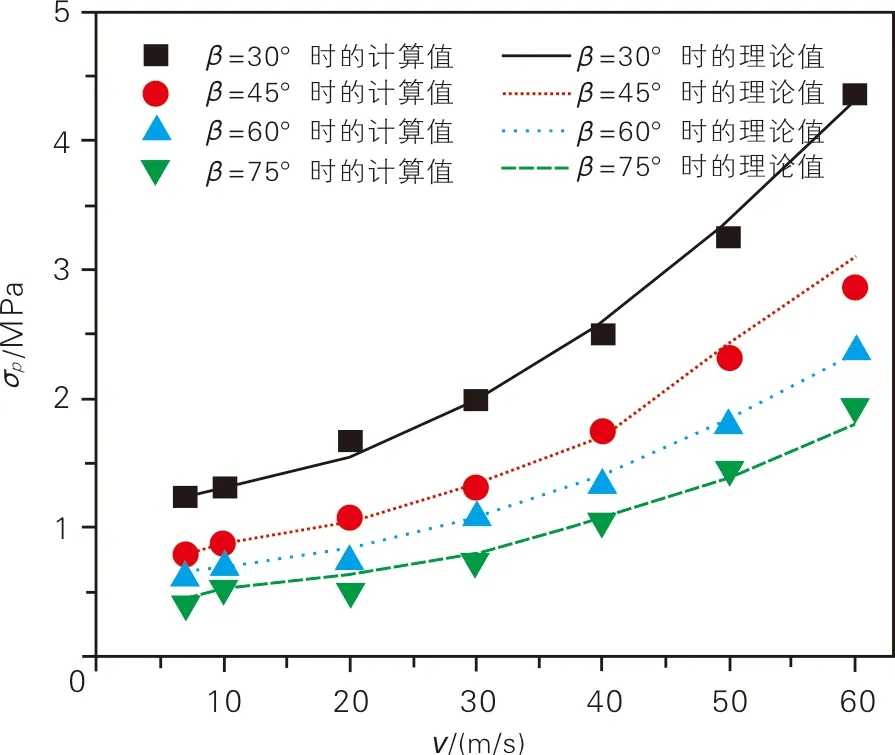
图9 平台应力的计算值与理论值对比

3 结论

采用ANSYS/LSDYNA软件探究了不同冲击速度和节点夹角下星型倾斜壁蜂窝结构的变形机制、应力-应变曲线及平台应力特性，得到如下结论。

1)当低速加载时，星型胞元先发生旋转形成塑性铰，然后从试件中下部开始颈缩，靠近冲击端蜂窝拉胀，直至压溃；当中速加载时，星型胞元仍发生旋转，先使胞元形成正“V”型剪切带，再逐渐形成“X”型剪切带，发生中部紧缩及上部拉胀，最后试件压溃；当高速加载时，蜂窝模型没有明显的颈缩现象，此时惯性效应成为引导蜂窝变形模式的主要因素。

2)低速加载时，不同节点夹角的蜂窝结构均产生双平台应力，提升了其对冲击的吸能能力。β=45°和60°时，应力-应变曲线中的平台应力段较长，且承受最大应力相对较大。

3)计算模型的数值模拟得到的平台应力和速度之间的关系与经验公式相符合，验证了经验公式的普适性。