考虑参数和边界条件不确定性的地下水污染随机模拟

徐亚宁,卢文喜*,王梓博,贾顺卿,王 涵,潘紫东

考虑参数和边界条件不确定性的地下水污染随机模拟

徐亚宁1,2,卢文喜1,2*,王梓博1,2,贾顺卿1,2,王 涵1,2,潘紫东1,2

(1.吉林大学,地下水与资源环境教育部重点实验室,吉林 长春 130012；2.吉林大学新能源与环境学院,吉林 长春 130012)

为了分析模型参数的随机变化和边界条件的随机变化对地下水溶质运移模型输出结果的不确定性影响,采用蒙特卡洛模拟对一假想算例展开研究,并结合风险评估阐述不确定性分析结果.首先,建立研究区地下水溶质运移数值模拟模型,并综合利用局部灵敏度分析和全局灵敏度分析方法筛选出对模型输出结果影响较大的参数,连同模型的边界条件(第一类边界条件—水头值)一起作为随机变量.然后,利用优化超参数的高斯过程回归(GPR)方法建立模拟模型的替代模型,代替模拟模型完成蒙特卡洛随机模拟.最后,对随机模拟的结果进行统计分析和区间估计,并利用污染物浓度的概率分布函数对1、2、3号观测井进行地下水污染风险评价.结果表明:置信水平>80%时,1,2,3号观测井污染物浓度值的置信区间分别为34.77～35.03,57.74～58.04, 100.07～100.69mg/L.此外,1,2,3号观测井为轻度污染的风险分别为6%,100%,100%;为中度污染的风险分别为0%,0%,99.6%;为重度污染的风险分别为0%,0%,0.5%,藉此为地下水污染修复防治和地下水的合理利用提供可靠参考依据.

边界条件不确定性；灵敏度分析；GPR替代模型；不确定性分析；风险评价

地下水模拟模型可用于地下水中污染物污染范围、运移途径、迁移转化规律等问题的科学研究,从而更好地防治地下水污染问题[1].但由于含水层和地质结构的复杂性、目前的理论水平和认识程度有限,地下水模拟模型不能完全刻画实际的地下水系统,地下水模拟具有一定的不确定性[2].因此,研究模型参数和边界条件中各时段水头值的不确定性对预测地下水污染物运移意义重大[3].

本文采用蒙特卡洛模拟方法分析地下水数值模拟不确定性问题.首先运用灵敏度分析方法筛选出对模拟模型输出结果影响较大的敏感参数.参数的灵敏度分析有局部和全局两类方法[4],其中局部灵敏度分析仅用于研究单个参数变化对模拟模型输出结果的影响,不同参数值变化对待分析参数灵敏度的影响被忽略,本文在采用局部灵敏度分析方法的基础上进一步应用全局灵敏度分析方法进行验证,对比分析两种方法的结果,使灵敏度分析结果更接近实际.

在进行蒙特卡洛模拟时,需要反复调用模拟模型,这将会产生巨大的计算负荷和冗长的计算过程.因此为减少反复调用地下水模拟模型产生的计算负荷,建立模拟模型的替代模型,以充分提高运算效率.替代模型是模拟模型输入输出响应关系的代替.近些年来替代模型被广泛应用于地下水领域,通过建立地下水模拟模型的替代模型有效提高计算效率,张将伟等[5]应用克里格法建立地表水地下水耦合模拟模型的替代模型并进行不确定性分析;侯泽宇等[6]应用克里格法、支持向量机法、核极限学习机法建立组合替代模型研究DNAPLs污染含水层修复方案优选问题;葛渊博等[7]利用克里格法和BP神经网络建立替代模型并进行蒙特卡洛模拟.本文分别针对3口观测井利用优化超参数的高斯过程回归(GPR)方法建立地下水模拟模型的替代模型,相较于前人所用方法,GPR法更容易实现,同时能够在数据中自主学习函数形式,且获得的结果具有概率意义[8-9],GPR替代模型调用简便,大幅度减少了计算负荷和计算时间,在保证计算精度的同时充分提高了计算效率.

地下水数值模拟的不确定性有模型的不确定性、资料的不确定性和参数的不确定性三种来源[10]. 参数的不确定性分析是影响地下水数值模拟结果可靠性的重要原因,目前主要用蒙特卡罗法、灵敏度分析方法等研究参数的不确定性问题,束龙仓等[11]利用蒙特卡洛方法,通过计算补给量及其相应可靠度研究参数的不确定性;Hassan等[12]利用GLUE方法分析并评价地下水流模型参数不确定性.由于地下水系统的复杂性以及人们认识的有限性,地下水模型边界的不确定性研究尤为重要,Hugman等[13]研究了定义模型边界条件的不确定性和季节性对地下水水量估计值的影响;李久辉等[14]研究边界条件不确定性并进行污染风险评估;Na等[15]分析了水文地质边界概化问题对地下水模型预测结果的影响.参数的不确定性是地下水数值模拟不确定性中最为重要的内容[10],因此,大多数研究只关注参数不确定性,却很少研究边界条件中各时段水头值不确定性对模拟模型输出结果的影响.但边界条件中各时段水头值的不确定性也是模型中重要的研究内容. 在地下水的数值模拟中,第一类边界条件经常出现[16],针对第一类边界条件进行研究,使地下水流场数值模拟更易于刻画、实现.与前人研究内容不同,本文的创新之处在于同时考虑了模型参数随机变化和第一类边界条件中各时段水头值的随机变化对模拟结果的不确定性影响,考虑问题更全面,令不确定性分析结果更接近实际.

本文将不确定性分析与地下水污染风险评价相结合,由相关资料和专业知识得到边界中不同时段的水头值取值范围以及水文地质参数取值范围后,综合运用局部灵敏度分析和全局灵敏度分析方法筛选出对模拟模型输出结果影响较大的参数,将其和边界中不同时段的水头值作为模型中的随机变量,为减少多次调用模拟模型产生的计算负荷,运用优化超参数的高斯过程回归(GPR)方法建立模拟模型的替代模型,并应用替代模型完成蒙特卡洛模拟过程.对蒙特卡洛随机模拟结果进行统计分析,利用概率分布函数估计不同置信程度的污染物浓度范围,进行地下水污染风险评价,令地下水污染预测结果更加科学,为地下水的合理利用提供可靠参考依据.

1 研究方法

1.1 蒙特卡洛方法

蒙特卡洛方法的主要思想是当要求解某个随机事件出现的概率,或是某个随机变量的期望值时,通过大量“试验”的方式,将在大量试验中出现的频率近似等于随机事件的概率[14].近年来,蒙特卡洛方法被广泛地应用于地下水模拟不确定性分析中[17].

1.2 灵敏度分析方法

灵敏度分析的方法分为两类:全局灵敏度分析法和局部灵敏度分析法[18],本文基于局部灵敏度分析方法进一步利用全局灵敏度分析方法进行验证,确定水文地质参数随机变量.

1.2.1 局部灵敏度分析法 就是将灵敏度系数较大的几个参数作为随机变量,其余参数为定值,研究模型输出结果的变化情况,优势是简单易操作,同时也保持了计算精度[4],公式如下:

式中:X表示当参数变化时对输出结果的影响程度,即灵敏度系数.

求取参数的灵敏度系数值时,保持其他所有参数不变,该参数的值由变化为+Da,同时因变量值由y()变化为y(+Da),通过下列计算公式获得其计算值,即:

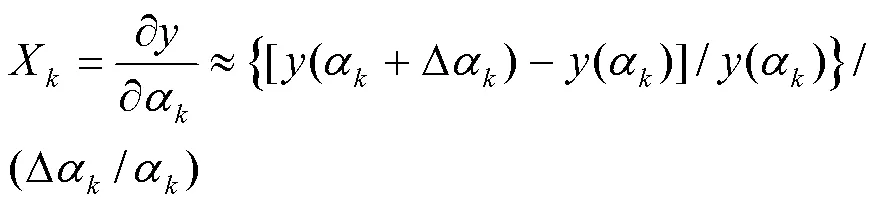
式(3)是不考虑单位下的计算公式.

1.2.2 全局灵敏分析方法 应用全局灵敏度分析方法可以得到更充分的信息,是因为它考虑了多个参数同时变化对模型输出结果的影响.Sobol法是基于方差分析系统内各输入变量对系统输出变量的影响的一种全局灵敏度分析方法,它可以处理非线性、非单调的函数和模型[19],计算各参数总灵敏度,计算公式如下:

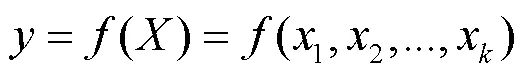
式中:表示个参数的模型目标函数.

模型输出方差表示为:

式中:D为x单独作用造成的输出方差;D是x和x间相互作用的方差;1,2…,k为个参数间相互作用的方差.

(5)式两边同时除以得到:

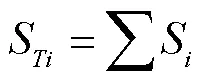
式中:S为总灵敏度,表示x对模型输出结果的总影响,S为所有包含x的灵敏度.

1.3 高斯过程回归(GPR)替代模型

与模拟模型相比,替代模型可以用更小的计算量得到近似的输出结果[20],是模拟模型的近似代替.地下水污染的随机模拟需要反复多次调用模拟模型,因此为减小计算负荷,建立地下水高斯过程回归(GPR)替代模型.

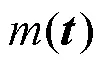
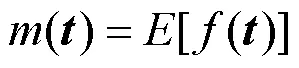
式中:和¢均为任意随机变量.故高斯过程(GP)可定义为

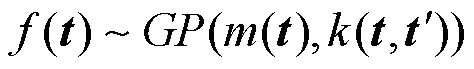
建立的关于回归问题的一般模型为:若观察目标值存在噪声,它与真实输出值相差:

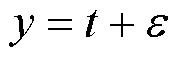
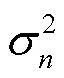
观察目标值集合的先验分布为

个训练样本输出和1个测试样本输出*所形成的联合高斯先验分布为:

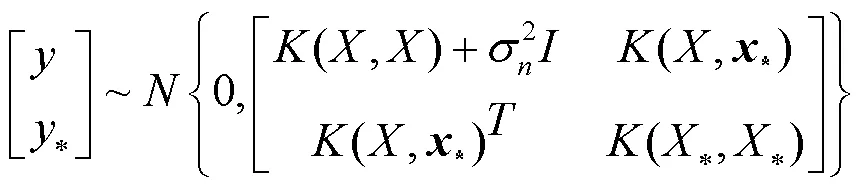
有不同的协方差函数供GP选择.GP 的协方差函数需要满足对任一点集都能够保证产生一个非负正定协方差矩阵.常用的协方差函数为:

2 应用研究

2.1 研究区概况

本文针对一个假想例子展开研究,如图1所示,研究区域东西长500m,南北宽300m,形状不规则,含水层概化为二维非均质各向同性潜水含水层,水流为二维非稳定流,含水层厚度为20m.研究区被划分为I、II、III区,其中含水层I区岩性主要为中砂,渗透系数为15m/d, II区岩性主要为中砂夹粗砂,渗透系数为20m/d, III区岩性主要为粗砂,渗透系数为32m/d.根据经验和所学知识,给出各参数的取值范围和概率分布[28-29],相关参数取值范围和概率分布见表1,其中因横向弥散度与纵向弥散度的比值为0.3,故只考虑纵向弥散度.本案例中将AB、CD边界概化为已知水头边界,AD、BC边界概化为隔水边界,地下水流向如图所示.

研究区内设有三口抽水井(同时作为观测井),编号分别为1,2,3号观测井.1,2,3号观测井定流量抽水,抽水流量分别为50,50,100m3/d.本次模拟时间为400d,每100d为一个模拟时段,共计4个模拟时段,在前两个模拟时段内以注水井的形式(100m3/d)持续恒定地向含水层中排放浓度为500mg/L的污染物,将污染物视为在迁移过程中不发生物理化学反应及吸附降解作用的氯化物.含水层中污染物的初始浓度为50mg/L.AB、CD边界概化为零浓度边界,AD、BC边界概化为零通量边界.

图1 污染源、观测井布设位置

表1 含水层各参数取值范围和概率分布

2.2 模型建立

在建立水文地质概念模型的基础上建立地下水水流模型和地下水溶质运移模型.

(1)地下水水流模型

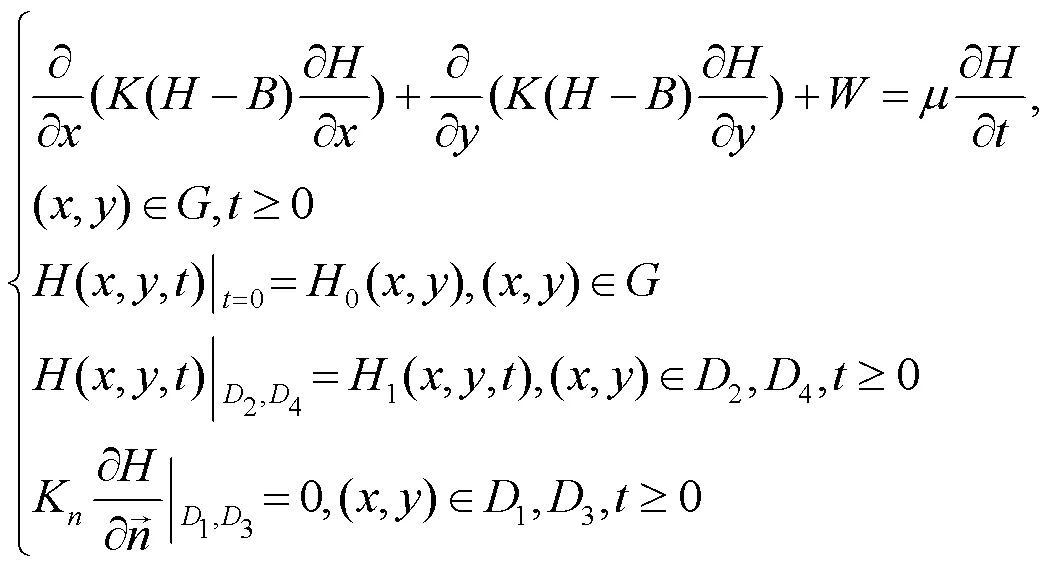
(2)地下水溶质运移模型

本次研究利用GMS软件中的MODFLOW模块和MT3DMS模块进行求解. 模型运行的100d, 200d,300,400d后污染物运移情况见图2,(I) (II) (III) (IV)分别代表100d,200d,300d,400d后污染物的运移情况 (本研究以模型运行后400d的结果进行计算).

2.3 确定随机变量

应用局部灵敏度分析方法的基础上进一步利用全局灵敏度分析方法进行验证,筛选出对模型输出结果影响较大的参数,对比两种方法结果,使分析结果更全面[30].参与本次灵敏度分析的参数有渗透系数、孔隙度、给水度、纵向弥散度,四个参数取值范围见上表1.各参数均值见下表2.

表2 含水层各参数均值

局部灵敏度分析方法是将各参数取均值分别增加、减少10%和20%,利用式(3)计算三口井的灵敏度系数,各井灵敏度系数值见下表3.

由图3可知,对于三口观测井,利用局部灵敏度分析方法研究时,潜水含水层渗透系数和孔隙度为两个影响最大的参数.

局部灵敏度分析仅研究单个参数变化对模拟模型输出结果的影响,在计算时保持其他参数不变,只改变某一待分析参数值,操作简便,但局部灵敏度分析方法忽略了不同参数取值变化对待分析参数灵敏度的影响,为进一步验证局部灵敏度分析结果的准确性,本次研究再利用Sobol法进行全局灵敏度分析,各参数的总灵敏度系数结果如图4所示.

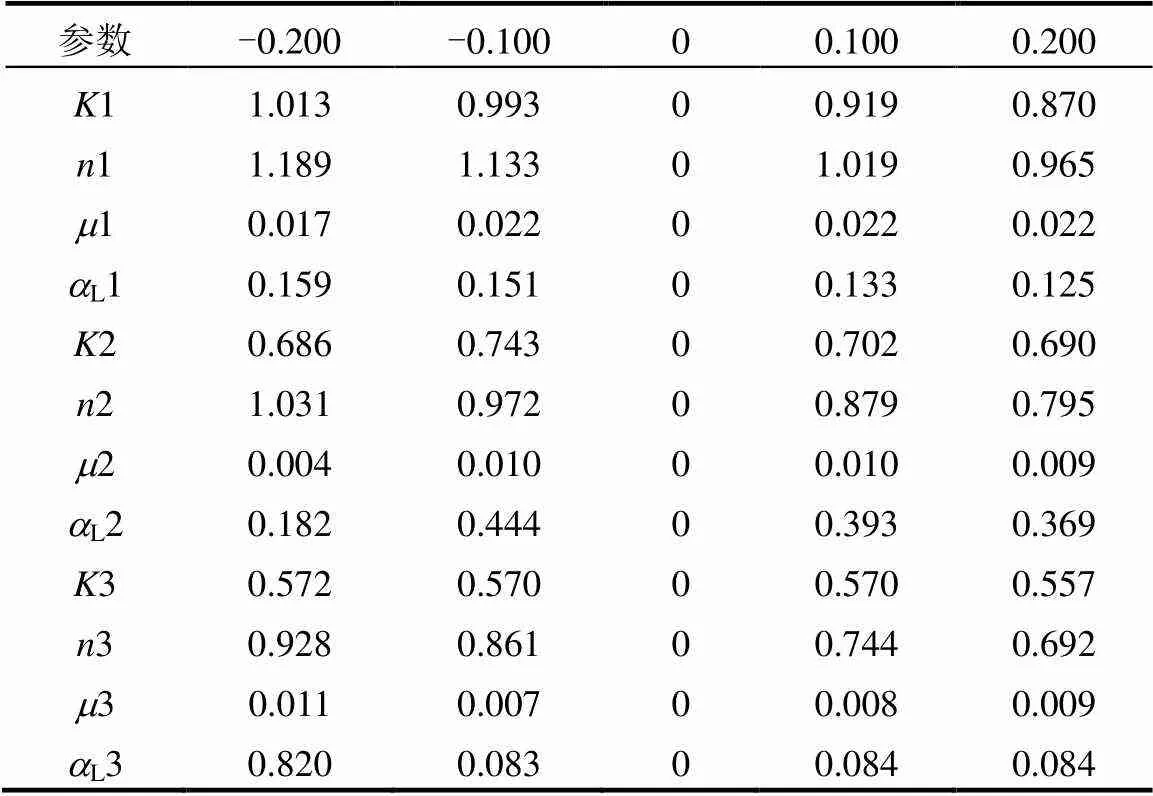
表3 各井各参数灵敏度计算结果

由两种灵敏度分析可知,对模型影响最大的参数是孔隙度和渗透系数,进一步验证了局部灵敏度分析结果的准确性.

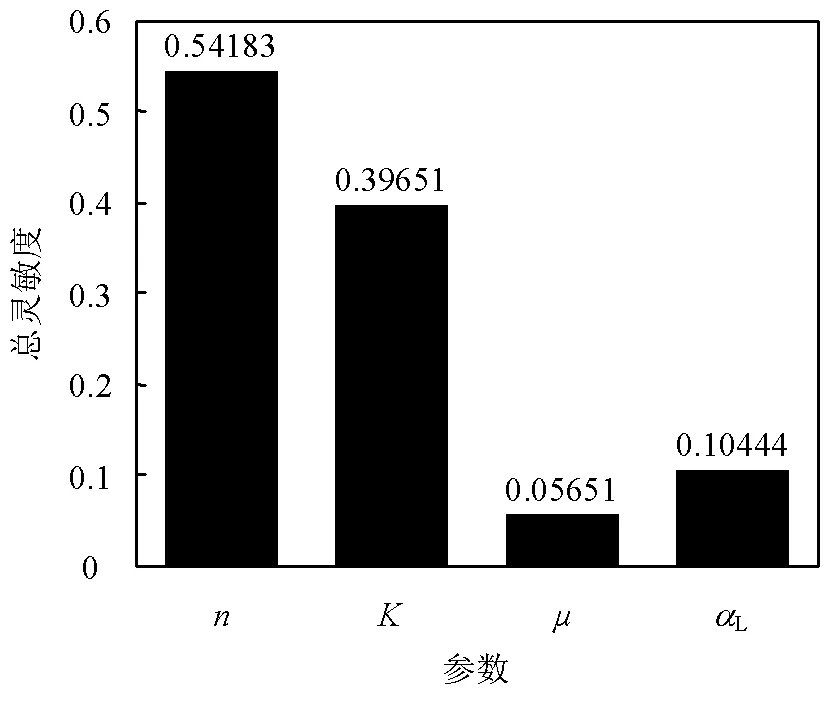
图4 全局灵敏度分析结果

考虑到边界条件的不确定性,本文主要研究第一类边界条件中各时段水头值不确定性(CD边界),根据相关资料的丰、平、枯水期的水头值得到各观测时段的水头取值范围.

故本研究中的随机变量为渗透系数、孔隙度以及CD边界各时段水头值,所以将、以及CD边界各时段水头值作为随机变量带入地下水溶质运移模型中,然后针对上述、和CD边界各时段水头值,使用拉丁超立方抽样方法进行随机抽样.

2.4 拉丁超立方抽样

本研究中替代模型输入变量为孔隙度、渗透系数以及CD边界各时段水头值,输出变量为污染物浓度值.建立替代模型需要一定的训练样本和检验样本,为了保证所抽取样本的代表性,使用拉丁超立方方法进行抽样.根据前人经验可知,孔隙度服从正态分布,渗透系数服从对数正态分布[31].应用此方法在随机变量变化范围内进行抽样,孔隙度和渗透系数概率分布及波动区间见表4,CD边界各时段水头值取值范围见表5.

表4 概率分布及波动区间

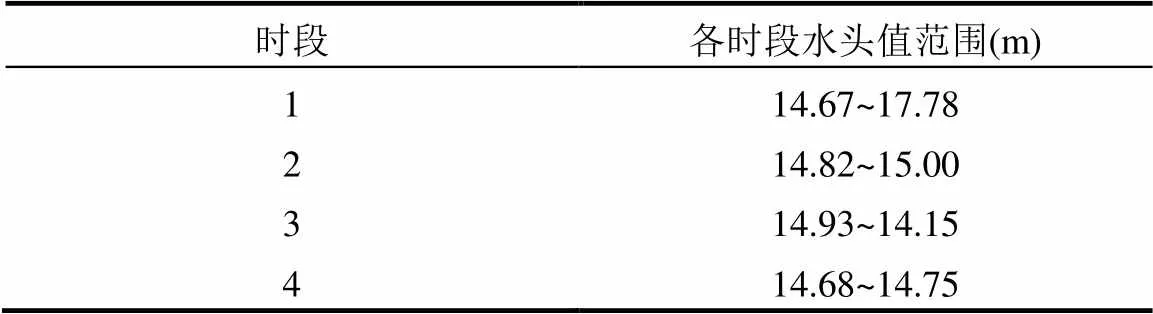
表5 各时段水头取值范围

通过拉丁超立方抽样获得300组样本,利用前250组输入——输出样本集分别建立三口观测井的地下水溶质运移GPR替代模型,为检验GPR替代模型对模拟模型的逼近程度,利用后50组评估逼近程度,选用确定性系数2、均方根误差RMSE、平均相对误差MRE、平均绝对误差MAE四个指标进行评估.具体计算公式如下:

(1)确定性系数2

(2)均方根误差(RMSE)

(3)平均相对误差(MRE)

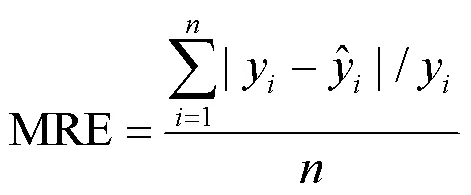
(4)平均绝对误差MAE

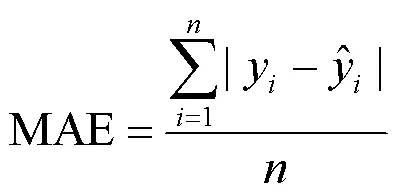
各评估指标见表6,由精度分析可知,GPR替代模型模型精度较高,误差较小,可以用来预测地下水污染物浓度.

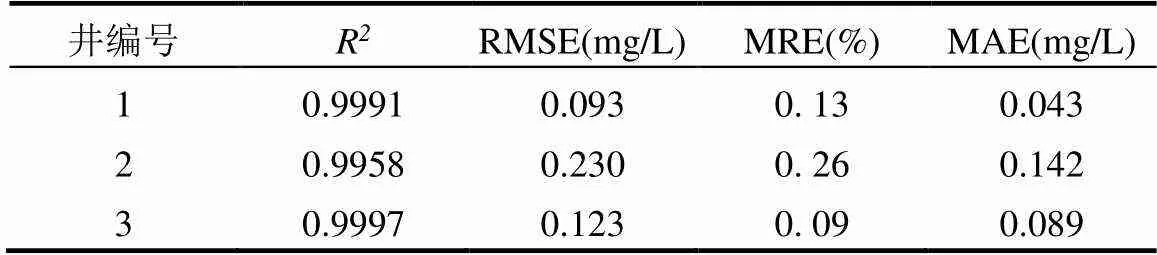
表6 高斯过程回归模型精度分析

2.5 蒙特卡罗随机模拟

研究区地下水污染的随机模拟利用蒙特卡罗方法实现.首先利用拉丁超立方方法对孔隙度、渗透系数及边界水头值三个随机变量进行抽样,得到 1000组参数组合;之后,将1000组参数组合输入到GPR替代模型中,分别得到3口井1000组污染物浓度的输出结果;最后,统计分析3口井的输出结果.减少了计算负荷的同时,又保持了一定的精度.

3 结果与讨论

利用优化超参数的GPR替代模型分别输出3口观测井第4时段末的1000组污染物浓度值,依据此数据,估计3口观测井在不同置信水平下的污染物浓度范围,并分析3口观测井遭受污染的风险.

3.1 统计分析

分析3口观测井第4时段末的1000组污染物浓度数据集的各项指标,并绘制各观测井的污染物浓度累计频次直方图(图5).由图5和表7可知,在第四个时段末,1号井污染物浓度在31.5～39mg/L时的概率最大,概率高达81.7%,可以预测1号井污染物浓度在31.5～39mg/L范围内的可能性最高.同理可以预测, 2、3号井污染物浓度在55～63mg/L和93.5～111mg/L范围内的可能性最高.井3遭受污染程度最严重,井2次之,井1遭受污染程度最小,由表7可以看出,2号井污染物浓度数据的变异系数较小,分布较集中;1号井污染物浓度数据的变异系数较大,分布较分散,表明在同一时间条件下,污染物浓度与不只与观测井距离污染源的位置有关,还需考虑地下水流向,顺地下水流向时,污染质运移距离越短,距离污染源越近,受含水层各参数的影响越小,污染物浓度输出的不确定性就越小.

利用SPSS软件的K-S检验分别对3口井的输出值进行分布检验(包括指数分布,均匀分布以及正态分布).检验结果显示,三口井的输出均服从正态分布,其中,1号井的输出均值为34.90,标准差为3.31;2号井的输出均值为57.89,标准差为3.66;3号井的输出均值为100.38,标准差为7.69.

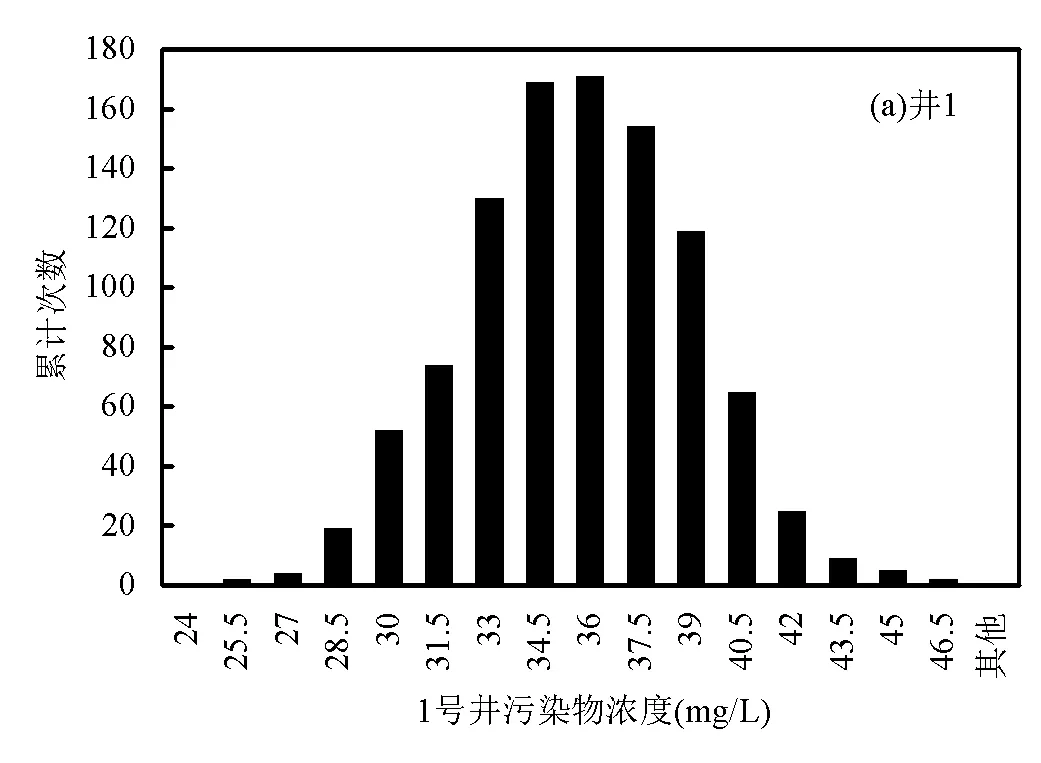
表7 各监测井污染物浓度输出值

3.2 污染物浓度区间估计

区间估计,是参数估计的一种形式,通过从总体中抽取的样本,在一定置信水平下,构造出适当的区间,以作为总体的分布参数(或参数的函数)的真值所在范围的估计.在本文将其引申,把各个观测井的输出值当做是要估计的参数,计算其在不同置信水平下的区间范围.由于3口井的输出均近似服从正态分布,故分别利用其概率分布函数进行区间估计.

由表8可以看出,置信水平越高,污染物浓度区间范围越大;置信水平越低,污染物浓度区间范围越小,越集中在均值附近.

表8 各井浓度值区间估计(mg/L)

3.3 地下水污染风险评价

分析三口观测井1000组GPR替代模型的污染物浓度,将其作为随机变量,绘制污染物浓度分布函数曲线,如下图6所示.根据计算结果,参照《地下水质量标准》(GB/T 14848-2017)[32],分析三口观测井中水质达到各类标准的概率.计算三口井第四时段末地下水污染物(氯化物)达到I、II、III类水质标准的概率,计算结果见表9.

由计算结果可知,1号井附近水质最好,为研究区地下水的合理利用提供了参考依据.同时人为规定污染物浓度超过40mg/L为轻度污染,超过 80mg/L 为中度污染,超过120mg/L为重度污染,各井污染物浓度超过40mg/L的概率分别为6%, 100%,100%;各井污染物浓度超过 80mg/L的概率分别为0%,0%,99.6%;各井污染物浓度超过120mg/L的概率分别为0%,0%,0.5%.据此结果可知,3号井有较大的污染风险,为日后地下水污染的防治提供合理依据.

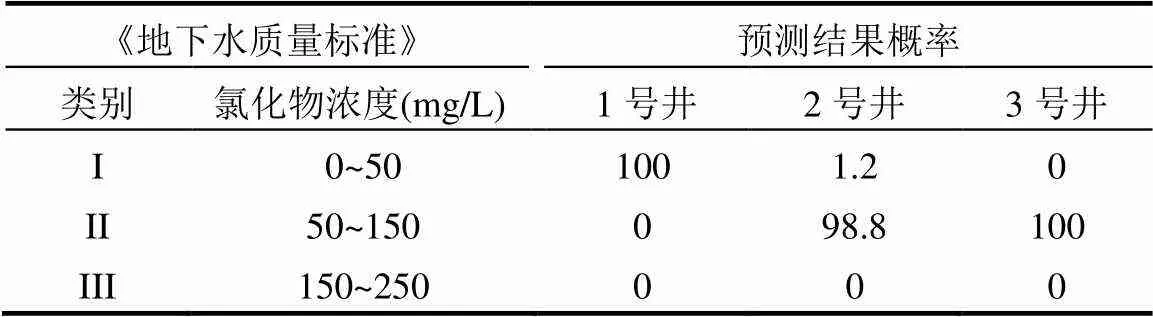
表9 各井达到水质标准概率 (%)

4 结论

4.1 通过综合运用局部灵敏度分析和全局灵敏度分析方法筛选出了对模拟模型输出结果影响较大的参数:渗透系数和孔隙度,有效降低了替代模型的输入变量维度,减小了计算负荷.

4.2 利用GPR法建立模拟模型的替代模型,大幅度减少了反复调用模拟模型产生的计算负荷,同时替代模型的计算结果能够很好地逼近模拟模型的计算结果,可以代替模拟模型进行后续工作.

4.3 本文同时分析了模型敏感参数的随机变化和第一类边界条件中各时段水头值的随机变化对地下水溶质运移模型输出结果的影响.运用蒙特卡洛方法进行地下水污染的随机模拟,并对随机模拟结果进行统计分析,利用污染物浓度概率分布函数对地下水遭受污染的风险进行评估,同时结合《地下水质量标准》(GB/T 14848-2017)[32],结果表明1号井附近水质最好;3号井水质有较大的污染风险,进而为地下水污染的防治和地下水的合理利用提供依据.

[1] 张晓烨,董增川.地下水模拟模型与优化模型耦合技术研究进展 [J]. 水北调与水利科技, 2012,10(2):142-144,149.

Zhang X Y, Dong Z C. Research progress to couple groundwater simulation model and optimization model [J]. South-to-North Water Transfers and Water Science & Technology, 2012,10(2):142-144,149.

[2] 吴吉春,陆 乐.地下水模拟不确定性分析 [J]. 南京大学学报(自然科学版), 2011,47(3):227-234.

Wu J C, Lu L. Uncertainty analysis for groundwater modeling [J]. Journal of Nanjing University(Natural Sciences), 2011,47(3):227-234.

[3] 顾文龙,卢文喜,马洪云,等.地下水数值模拟分析中降水入渗补给强度及渗透系数不确定性评价 [J]. 水电能源科学, 2015,33(11):45- 48,64.

Gu W L, Lu W X, Ma H Y, et al. Uncertainty evaluation of precipitation infiltration rate and hydraulic conductivity in groundwater numerical simulation analysis [J]. Water Resources and Power, 2015,33(11):45-48,64.

[4] 束龙仓,王茂枚,刘瑞国,等.地下水数值模拟中的参数灵敏度分析 [J]. 河海大学学报(自然科学版), 2007,35(5):491-495.

Shu L C, Wang M M, Liu R G, et al. Sensitivity analysisofparametersin numerical simulation ofgroundwater [J]. Joumal of Hohai University (Natural Sciences), 2007,35(5):491-495.

[5] 张将伟,卢文喜,曲延光,等.基于Monte Carlo方法的地表水地下水耦合模拟模型不确定分析 [J]. 水利学报, 2018,49(10):1254-1264.

Zhang J W, Lu W X, Qu Y G, et al. Uncertainty analysis of surface water and groundwater coupling simulation model based on Monte Carlo method [J]. Journal of Hydraulic Engineering, 2018,49(10): 1254-1264.

[6] 侯泽宇,王 宇,卢文喜.地下水DNAPLs污染修复多相流模拟的替代模型 [J]. 中国环境科学, 2019,39(7):2913-2920.

Hou Z Y, Wang Y, Lu W X. Surrogate models of multi-phase flow simulation model for DNAPL-contaminated aquifer remediation [J]. China Environmental Science, 2019,39(7):2913-2920.

[7] 葛渊博,卢文喜,王梓博,等.基于BP神经网络替代模型的地下水污染随机模拟 [J]. 中国农村水利水电, 2022,(3):107-113,119.

Ge Y B, Lu W X, Wang Z B, el at. Random simulation of groundwater pollution based on BP neural network substitution model [J]. China Rural Water and Hydropower, 2022(3):107-113,119.

[8] 何志昆,刘光斌,赵曦晶,等.高斯过程回归方法综述 [J]. 控制与决策, 2013,28(8):1121-1129,1137.

He Z K, Liu G B, Zhao X J, el at. Overview of Gaussian process regression [J]. Control and Decision, 2013,28(8):1121-1129,1137.

[9] 刘宸博,邢 帅,王丹菂,等.一种高斯过程回归的水体吸收系数反演模型 [J]. 测绘科学技术学报, 2021,38(4):384-390.

Liu C B, Xing S, Wang D D, el at. Absorption coefficients inversion model based on gaussian process regression [J]. Journal of Geomatics Science and Technology, 2021,38(4):384-390.

[10] 高 烨,梁收运,王申宁,等.地下水数值模拟不确定性分析研究进展 [J]. 地下水, 2020,42(1):28-31,97.

Gao Y, Liang S Y, Wang S N, el at. Research progress on uncertainty analysis of groundwater numerical simulation [J]. Underground Water, 2020,42(1):28-31,97.

[11] 束龙仓,陶玉飞,刘佩贵.考虑水文地质参数不确定性的地下水补给量可靠度计算 [J]. 水利学报, 2008,39(3):346-350.

Shu L C, Tao Y F, Liu P G. Reliability calculation method for groundwater recharge in consideration of uncertainty of hydrogeological parameters [J]. Journal of Hydraulic Engineering, 2008,39(3):346-350.

[12] Hassan A E, Bekhit H M, Chapman J B. Uncertainty assessment of a stochastic groundwater flow model using GLUE analysis [J]. Journal of Hydrology, 2008,362(1/2):89-109.

[13] Hugman R, Stigter T Y, Monteiro J P, et al. Modeling the spatial and temporal distribution of coastal groundwater discharge for different water use scenarios under epistemic uncertainty: case study in South Portugal [J]. Environmental Earth Sciences, 2015,73(6):2657-2669.

[14] 李久辉,卢文喜,常振波,等.基于不确定性分析的地下水污染超标风险预警 [J]. 中国环境科学, 2017,37(6):2270-2277.

Li J H, Lu W X, Chang Z B, et al. Risk prediction of groundwater pollution based on uncertainty analysis [J]. China Environmental Science, 2017,37(6):2270-2277.

[15] Na H N, Koo M H, Cha J H, et al. Sensitivity analysis of groundwater model predictions associated with uncertainty of boundary conditions: A case study [J]. Journal of Soil and Groundwater Environment, 2007,12(3):53-65.

[16] 邹立芝.数值法计算中边界条件处理方法的探讨 [J]. 长春地质学院学报, 1992,(2):199-202.

Zou L Z. Discussion on processing method of boundary conditions in numeracal calculation [J]. Journal of Changchun University of Earth Science, 1992,(2):199-202.

[17] Atanassov E, Dimov I T. What Monte Carlo models can do and cannot do efficiently? [J]. Applied Mathematical Modelling, 2008,32(8): 1477-1500.

[18] Luo J, Lu W. Sobol sensitivity analysis of NAPL-contaminated aquifer remediation process based on multiple surrogates [J]. Computers & Geosciences, 2014,(67):110-116.

[19] Nossent J, Elsen P, Bauwens W. Sobol' sensitivity analysis of a complex environmental model [J]. Environmental Modelling & Software, 2011,26(12):1515-1525.

[20] 欧阳琦,卢文喜,侯泽宇,等.基于替代模型的地下水溶质运移不确定性分析 [J]. 中国环境科学, 2016,36(4):1119-1124.

Ou Y Q, Lu W X, Hou Z Y, et al. Uncertainty analysis of groundwater solute transport based on surrogate model [J]. China Environmental Science, 2016,36(4):1119-1124.

[21] Rasmussen C E, Williams C. Model Selection and Adaptation of Hyperparameters [C]. MIT Press, 2005.

[22] 谢建雄,鲁铁定.一种优化高斯过程回归的隧道围岩变形预测方法 [J]. 测绘科学, 2021,46(4):50-56.

Xie J X, Lu T D. A deformation prediction method for tunnel surrounding rock based on optimizing Gaussian process regression [J]. Science of Surveying and Mapping, 2021,46(4):50-56.

[23] Rasmussen C E, Williams C. Gaussian Processes for Machine Learning [M]. Gaussian Processes for Machine Learning, 2005.

[24] 苏国韶,张 研,张小飞.高斯过程机器学习方法在地下水位预测中的应用 [J]. 中国农村水利水电, 2008,(12):48-50,54.

Su G S, Zhang Y, Zhang X F. Application of Gaussian Process Machine Learning to the Prediction of Groundwater Level [J]. China Rural Water and Hydropower, 2008,(12):48-50,54.

[25] 叶 婧.基于高斯过程回归的锂电池数据处理 [D]. 北京:北京交通大学, 2016.

Ye J. Research on Lithium-ion battery data processing based on Gaussian Process Regression [D]. Beijing: Beijing Jiaotong University, 2016.

[26] Sundararajan S, Keerthi S S. Predictive approaches for choosing hyperparameters in Gaussian Processes [J]. Neural Comput, 2001, 13(5):1103–1118.

[27] 曹文梁,康岚兰.高斯过程回归超参数自适应选择粒子群优化算法 [J]. 合肥工业大学学报(自然科学版), 2019,42(11):1479-1484.

Cao W L, Kang L L. Particle swarm optimization for adaptive hyper-parameters acquisition of Gaussian process regression [J]. Journal of Hefei University of Technology(Natural Science), 2019, 42(11):1479-1484.

[28] 陈 彦,吴吉春.含水层渗透系数空间变异性对地下水数值模拟的影响 [J]. 水科学进展, 2005,16(4):482-487.

Chen Y, Wu J C. Effect of the spatial variability of hydraulic conductivity in aquifer on the numerical simulation of groundwater [J].Advances in Water Science, 2005,16(4):482-487.

[29] 林 青,徐绍辉.基于GLUE方法的饱和多孔介质中溶质运移模型参数不确定性分析 [J]. 水利学报, 2012,43(9):1017-1024.

Lin Q, Xu S H. Parameter uncertainty analysis of solute transport in saturated porous media based on GLUE method [J]. Journal of Hydraulic Engineering, 2012,43(9):1017-1024.

[30] 王 涵,卢文喜,李久辉,等.地下水 DNAPLs污染多相流的随机模拟及其不确定性分析 [J]. 中国环境科学, 2018,38(7):2572-2579.

Wang H, Lu W X, Li J H, et al. Stochastic simulation and uncertainty analysis of multi-phase flow of groundwater polluted by DNAPLs [J]. China Environmental Science, 2018,38(7):2572-2579.

[31] 侯泽宇,卢文喜,王 宇.基于替代模型的地下水DNAPLs污染源反演识别 [J]. 中国环境科学, 2019,39(1):188-195.

Hou Z Y, Lu W X, Wang Y. Surrogate-based source identification of DNAPLs-contaminated groundwater [J]. China Environmental Science, 2019,39(1):188-195.

[32] GB/T 14848-2017 地下水质量标准 [S].

Stochastic simulation of groundwater pollution considering uncertainty of parameters and boundary conditions.

XU Ya-ning1,2, LU Wen-xi1,2*, WANG Zi-bo1,2, JIA Shun-qing1,2,WANG Han1,2, PAN Zi-dong1,2

(1.Key Laboratory of Groundwater Resources and Environmental, Ministry of Education, Jilin University, Changchun 130012, China；2.College of New Energy and Environment, Jilin University, Changchun 130012, China)., 2022,42(7)：3244～3253

In order to investigate the influences of random changes in model parameters and boundary conditions on the output uncertainty of groundwater solute transport model, combined application of Monte Carlo simulation and risk assessment were applied to illustrate the uncertainty analysis results of a hypothetical example. Firstly, a numerical simulation model of groundwater solute transport was established, then the parameters with greater impacts on the model output screened by local and global sensitivity analysis, together with the boundary conditions of the model (the first type of boundary conditions—head value) were set as random variables.Then the Gaussian Process Regression (GPR) method of optimizing hyperparameters was employed to establish an alternative model of the simulation model to complete the Monte Carlo stochastic simulation. Finally, statistical analysis and interval estimate of the results of random simulation were carried out, and the probability distribution function of pollutant concentration was used to estimate the risk of different degrees of pollution of observation wells 1, 2, and 3. The results show that when the confidence level was greater than 80%, the confidence intervals of the pollutant concentration values in observation wells 1, 2, and 3 were 34.77～35.03, 57.74～58.04, and 100.07～100.69mg/L, respectively. In addition, in observation wells 1, 2, and 3, the risk of slight pollution was 6%, 100% and 100%, respectively; the risk of moderate pollution was 0%, 0% and 99.6%, respectively; the risk of heavy pollution was 0%, 0%, and 0.5%, respectively. The present study can provide a reliable reference for pollution remediation and rational utilization of groundwater.

uncertainty of boundary conditions；sensitivity analysis；GPR substitution model；uncertainty analysis；risk assessment

X523

A

1000-6923(2022)07-3244-10

徐亚宁(1999-),女,河北保定人,吉林大学硕士研究生,主要从事地下水数值模拟方面研究.

2021-12-14

国家自然科学基金资助项目(41972252);国家重点研发计划资助项目(2018YFC1800405)

* 责任作者, 教授, luwx999@163.com