地下水污染模拟模型的不确定性分析

罗成明,卢文喜*,王梓博,常振波

地下水污染模拟模型的不确定性分析

罗成明1,2,卢文喜1,2*,王梓博1,2,常振波1,2

(1.吉林大学,地下水与资源环境教育部重点实验室,吉林 长春 130012；2.吉林大学新能源与环境学院,吉林 长春 130012)

为同时分析源汇项和水文地质参数不确定性对地下水污染数值模拟模型输出结果的影响,以抚顺市某煤矸石堆放场为研究实例展开研究.首先以硫酸根离子作为模拟因子,建立该场地地下水污染数值模拟模型.然后,分别采用局部灵敏度分析和全局灵敏度分析两种方法对模拟模型参数进行灵敏度分析并对比二者的结果,最终筛选出对模型输出结果影响较大的两个参数作为模型的随机参数.为减少反复调用模拟模型产生的计算负荷,分别对3口观测井应用克里格、核极限学习机、支持向量机和BP神经网络4种方法建立模拟模型的替代模型,根据这4种替代模型在不同井的拟合效果,为每口井优选出一个表现最好的替代模型,并利用优选出的替代模型完成蒙特卡洛随机模拟.最后,对随机模拟的结果进行统计分析与风险评估.结果表明,在置信度为80%时,1,2,3号三口井浓度的置信区间分别为:211.48～845.04mg/L,0～406.98mg/L,231.42～958.37mg/L.此外,依据《地下水质量标准》和各井的污染物浓度分布函数曲线得出:1号井和3号井的水质达标Ⅴ类水的概率分别为90.1%和93.1%,2号井达标Ⅲ类水的概率为80.7%,藉此为地下水资源管理和污染防治提供合理依据.

地下水污染随机模拟；灵敏度分析；替代模型；不确定性分析；风险评估

地下水模拟模型可以用来描述地下水水流运动和溶质运移规律,是地下水资源管理和污染防治的重要技术手段.然而,在人为因素以及自然因素的双重影响下,地下水数值模拟模型存在不确定性,导致模型输出结果存在不确定性[1].

近年来地下水溶质运移的不确定分析发展迅速.Li等[2]将不确定性分析应用到风险评估方面,分析了天津市南水北调工程取水区浅层和深层地下水的风险值.王梓博等[1]、常振波等[3]通过蒙特卡罗方法分析了水文地质参数不确定性;李久辉等[4]考虑了边界条件不确定性对污染质运移结果的影响;袁乾等[5]同时考虑了水文地质参数及源汇项中“源”的不确定性.在实际情况中,水文地质参数及源汇项的不确定性对地下水模拟模型输出结果的不确定性影响显著.然而,在目前地下水溶质运移不确定性的研究中,考虑单因素不确定性的研究较多,而同时考虑多因素不确定性的研究较少,本文同时考虑水文地质参数及源汇项中的“汇”进行不确定性分析.

在不确定性分析的过程中将会多次调用模拟模型,这会带来极大的计算负荷,而替代模型不仅可以大幅减少计算负荷还可以保证较高的逼近精度.此前,高鑫宇等[6]将改进稀疏网格替代模型应用于地下水DNAPLs运移数值模拟的不确定性中,降低了计算耗时.侯泽宇等[7]同时应用克里格、核极限学习机和支持向量机3种方法建立集对权组合替代模型,大幅减少模拟-优化过程的计算负荷.葛渊博等[8]将机器学习方法引用于不确定分析中,利用BP神经网络方法建立替代模型,保证了较高的精度.在前人的研究中,对于场地多口观测井替代模型的建立采用的都是相同的方法.然而,在研究问题较为复杂且存在多口监测井的情况下,某种单一方法所建立的替代模型并不具备普适性,很难同时满足所有井的精度要求.针对该问题,本文分别对研究区内3口井利用克里格、核极限学习机、支持向量机和BP神经网络4种方法建立替代模型,经过对比分析,为每口井分别优选出表现最高的一种替代模型,以此提高模拟模型的逼近精度.

综上,本文以抚顺市某煤矸石堆放场为研究实例,同时分析源汇项和水文地质参数不确定性对地下水污染数值模拟模型输出结果的影响.根据场地的实际情况及污染物特征,本文选取硫酸根离子为模拟因子,建立该场地的地下水污染数值模拟模型.同时应用局部和全局灵敏度分析两种方法对参数进行灵敏度分析并对比二者的分析结果,筛选出灵敏度较大的两个参数作为模拟模型的随机参数.为减少多次调用模拟模型产生的巨大计算负荷,分别应用克里格、核极限学习机、支持向量机和BP神经网络4种方法建立模拟模型的替代模型,根据这四种替代模型在不同井的拟合效果,分析对比筛选出场地各井精度最高的替代模型,并利用优选出的替代模型完成蒙特卡洛随机模拟.最后对该研究区随机模拟的结果进行统计分析与区间估计,进行地下水污染风险评估,为地下水污染防治提供科学依据.

1 研究方法

1.1 蒙特卡罗法

蒙特卡罗方法是以概率统计理论为基础的一种方法.在具体的问题中,通常采用成百数千次的模拟,统计得到各个事件发生的概率或者各事件观测值的算术平均值,借此得到问题的解.利用蒙特卡罗方法进行不确定性研究可将地下水数值模拟各因素(参数,源汇项等)的不确定性转化成输出结果的不确性,利于问题的研究.

1.2 灵敏度分析法

利用灵敏度分析法来筛选出对模拟模型结果影响最大的参数,以该参数为随机变量不仅会减少替代模型的维度,还可以减少计算负载[9].在目前的灵敏度分析方法中,包括局部灵敏度分析和全局灵敏度分析[10].本文将采用这两种方法,分别求得地下水模拟模型参数的灵敏度,并将二者的结果进行对比分析,局部灵敏度分析方法作为试验方法,全局灵敏度方法作为验证方法,更准确的选出灵敏度较大的参数.

(1)局部灵敏度分析主要目的是选择影响最大的因素,其公式如下:

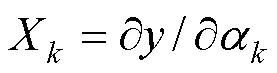
式中:X为灵敏度系数;为了方便计算以及不同参数灵敏度的比较,通常采用无量纲的形式:

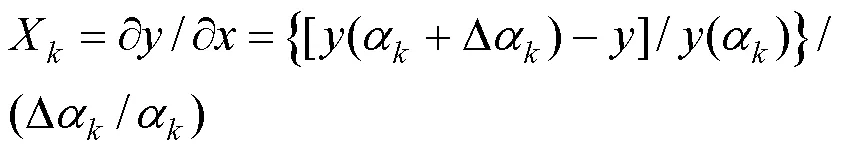
式中:X表示参数α变化时对输出结果的影响程度,X越大说明参数的变化对输出结果影响越大.

(2)全局灵敏度分析是基于局部灵敏度分析的不足进行改进.相比于局部灵敏度分析,全局灵敏度能够考虑不同参数对研究对象的共同影响,这也更加的契合于实际问题.目前全局灵敏度的分析方法较多,如基于差分分析的sobol法[11],多元回归法[12]以及Morris方法[13]等.本文采用Morris方法进行模型参数的全局灵敏度分析.Morris方法着重在于参数的取值以及依据参数的重要性进行排序[14],该方法取值抽样时,一次只改变一个参数,假设地下水模型需要分析的参数个数为个,则会轮流计算个参数的目标函数值[15].根据以下公式可以计算每个参数的基效应:

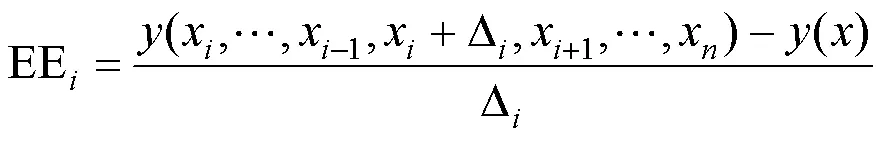
EE为第个参数变化引起的变化效应.为了方便不同参数的对模型的影响度进行比较,对影响度进行修正:

(4)

每个参数可有多种取值,最终取均值:

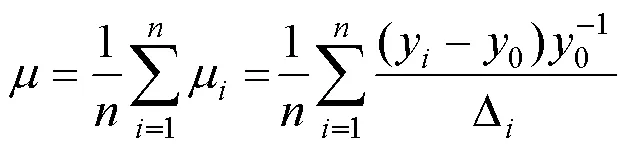
式中:D为某一参数的变化;为单个参数单次取样的影响值;为单个参数多次取样后的影响均值.

1.3 替代模型

替代模型在多学科领域内应用广泛,其基本原理是通过已知的输入-输出样本集构造同模型相拟合的近似函数,借此得到模型的输出结果.在分析地下水模拟不确定性的过程中,为了减少反复调用模拟模型产生的大量计算负荷选择建立模拟模型的替代模型.本文分别采用BP神经网络(BPNN)方法、核极限学习机(KELM)方法、支持向量机(SVR)方法以及克里格(KRG)方法建立模拟模型的替代模型,并分别对比4种方法,针对各个观测井的精度好坏,选出每个观测井精度最好的替代模型,进行后续的随机模拟研究.

1.3.1 BP神经网络方法 BP神经网络的核心是根据每次训练得到的结果与预想结果进行误差分析,之后修改阈值和权重,不断反复多次的训练,进而得到同模拟模型输出值相吻合的结果.浅显的理解就是根据反馈不断更新迭代,以达到优化的目的.BP神经网络通常由三层组成:输入层、隐含层和输出层;计算过程分为两个阶段:信息正向传播与误差的反向传播过程[16].其简易结构如图1所示.

(1)信息正向传播过程:让信息通过输入层进入网络,每一层网络都将对其进行计算,然后得到最终输出结果的过程BP神经网络常采用的传递函数Sigmoid函数,此函数是非线性变换函数,一般采用:

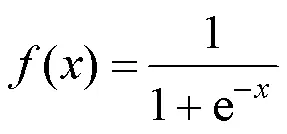
正向传输的输出层计算公式如下:

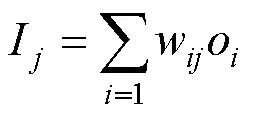
式中:O代表神经元的输出;W为神经元与神经元连接的权重.

(2)逆向传播过程:逆向反馈从最后一层即输出层开始,第一次的正向反馈的权重随机赋值,为了达到目标优化的效果,此时需要调整整个网络的参数即权重值,对网络调整的依据是输出层输出值与类别之间的差异.

对于输出层:

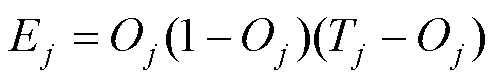
式中:E表示第个节点的误差值;O表示第个节点的输出值;T记录输出值.

中间隐层通过下层节点总误差按权重累加:

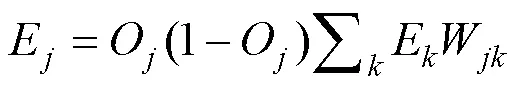
式中:E为下一层节点的误差率;W为当层节点到下层节点的权重值.

计算误差后可利用误差率对权重进行更新:

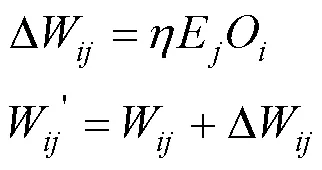
式中:h为学习速率,取值范围在(0.1),一般小于0.5[17].

1.3.2 核极限学习机方法 核极限学习机(KELM)基于极限学习机(ELM),将核函数引入后者的训练中,将传统的随机映射替换成映射,大幅提高了后者的拟合及分类的能力[18].KELM的基本原理如下:

对于训练样本,ELM的输出y可表示为:

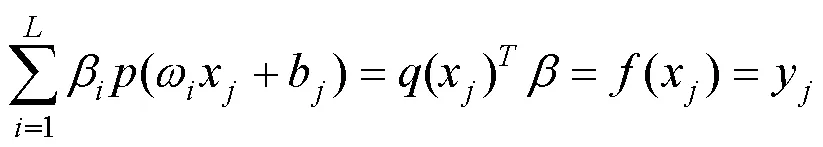
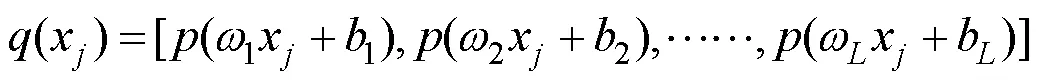
经过一系列的优化及化简,KELM输出函数的表达公式如下:

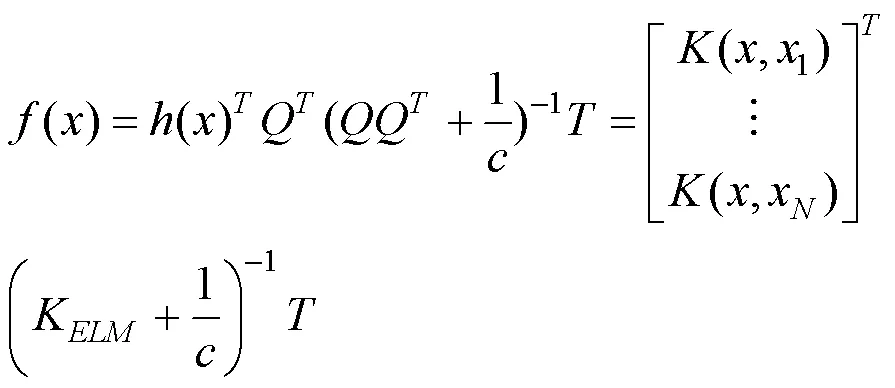
1.3.3 克里格方法 克里格方法的核心是在范围有限的研究区内,利用变量的相互契合性和随机变化性搭建成该方法的基本结构,然后对区域中变量的取值进行误差最小的优化估计.该方法将输入与输出变量之间的关系以回归方程的形式表达出来,其公式如下:

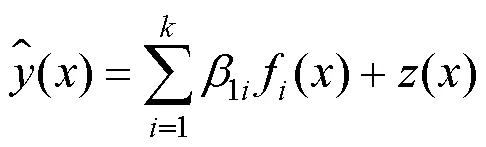
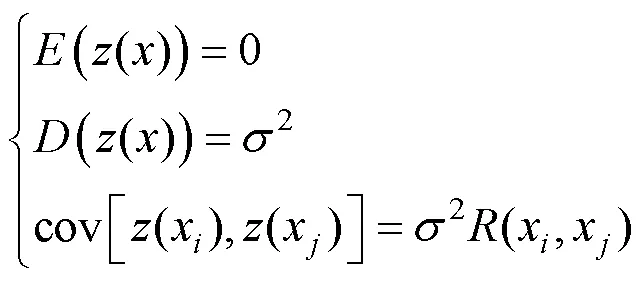
目前常用的模型为高斯模型,模型如下:

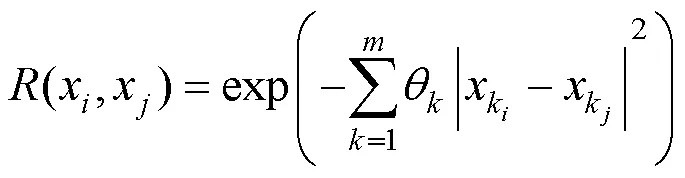
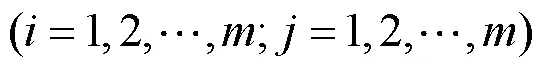
1.3.4 支持向量机方法 支持向量机所采用的并非为传统统计学上的经验风险最小化原理,而是一种全新的通用机器学习方法:结构风险最小化原理,该种方法也更加的贴合目前阶段的科学研究.支持向量机的核心在于回归的思想,而回归的核心是借以非线性映射函数把输入数据映射到高维空间进行线性回归.方程可表示为:

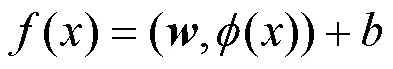
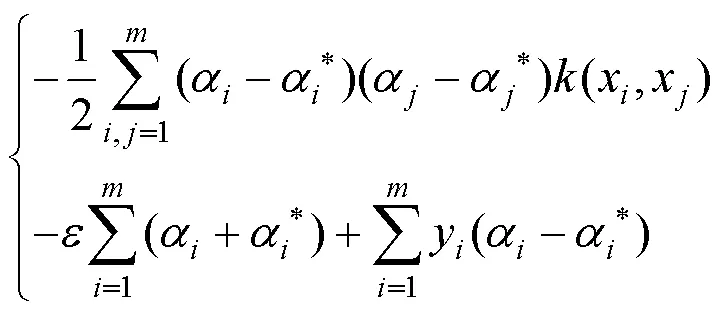
最后得到:

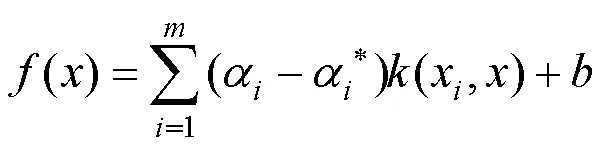
2 应用研究

2.1 概况

本文以抚顺市某煤矸石堆至浑河圈定的地区作为本次地下水数值模拟的研究对象.研究区东西长约9700m,南北宽约6300m,总面积约52.35km2,其地势东高西低,地下水流向大体上自东向西.将研究区概化为非均质各向同性含水层,主要研究对象为一层潜水含水层,厚度约8m,水流为二维稳定流,根据研究区含水层的渗透性可分为两个区域.研究区示意图详见图2.

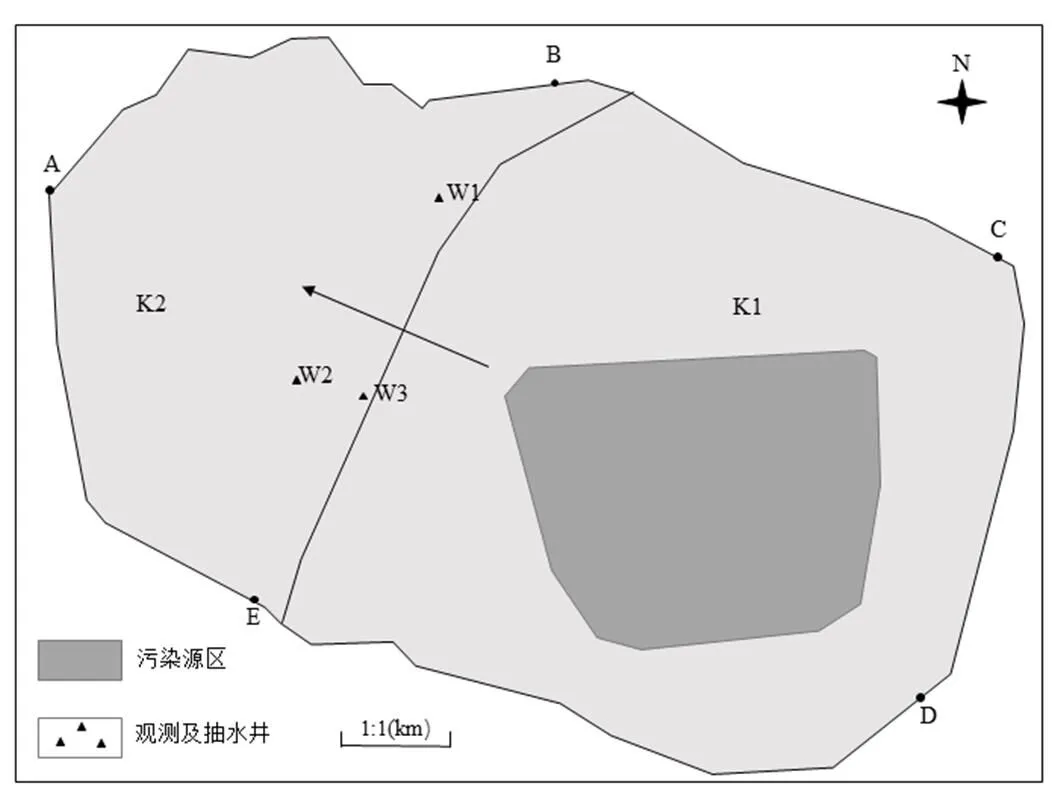
图2 研究区概况

研究区北部边界AB为浑河,概化为已知水头边界;东北部边界BC和南部边界DE平行于区内地下水流线,概化为零通量边界;将研究区东部边界CD概化为侧向径流补给边界;西南部边界EA概化为侧向径流排泄边界,侧向径流边界概化为已知流量边界.在溶质运移模型中,研究区北部边界AB和西南部边界EA概化为已知对流-弥散通量边界;东北部边界BC和南部边界DE由于没有对流作用,概化为零通量的水动力弥散通量边界;东部边界CD概化为已知浓度边界.将历史水位资料的均值作为水流模型的初始条件;将硫酸根离子的环境基底值(零浓度)作为溶质运移模型的初始条件.

此次的研究考虑源汇项的影响,根据实际的踏勘情况以及当地居民的用水情况设置三口观测井兼抽水井(W1～W3).考虑实际场地污染物所占的比重以及物理化学性质,选定硫酸根离子作为此次污染物研究对象.对实际场地的地下水流模型以及溶质运移模型的校正得表1参数取值,污染源硫酸根离子的释放强度为7000mg/d.抽水井用水量取值如表2所示.

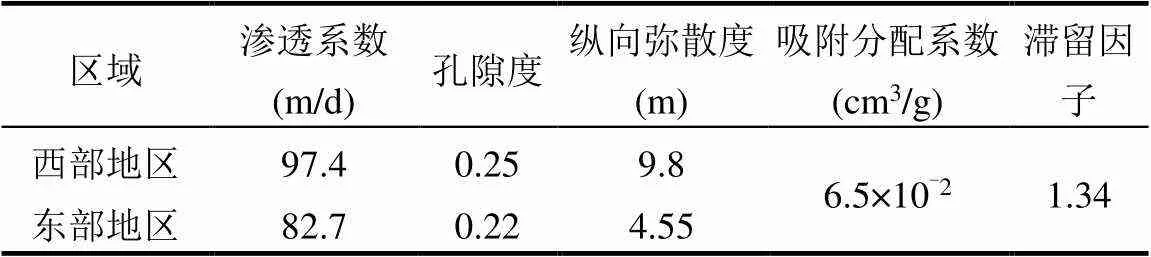
表1 模型水文地质参数校正后取值

表2 抽水井年用水量

2.2 模型建立

2.2.1 数值模拟 充分考虑研究区的水文地质条件,并在地下水概念模型的基础上,建立地下水水流模型和溶质运移模型,后者是在前者的基础上建立的.

(1)水流模型:

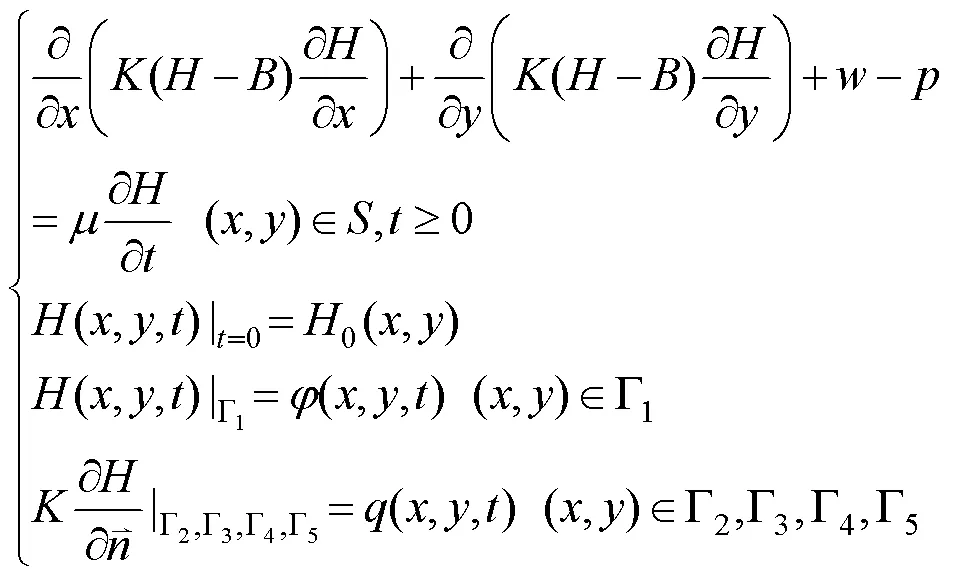
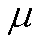
(2)溶质运移模型:

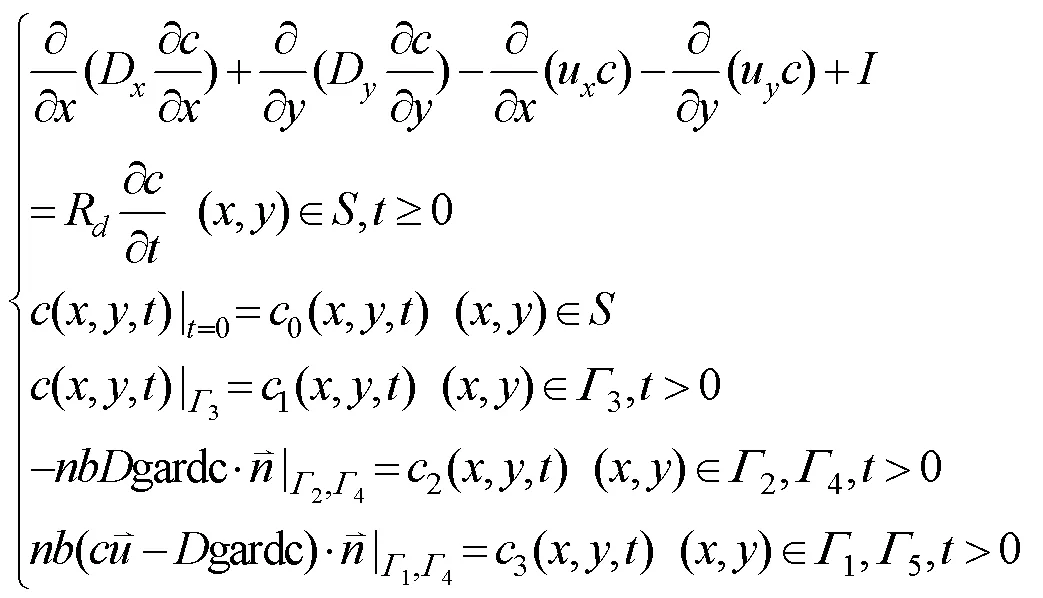
本文的地下水水流模型和溶质运移模型是运用GMS中MODEFLOW板块和MT3D板块求解.给模型输入校正后的水文地质参数,抽水井W1的抽水量为18250m3/a, 抽水井W2的抽水量为25550m3/a, 抽水井W1的抽水量为36500m3/a,预报20a后的地下水污染状况(图3).

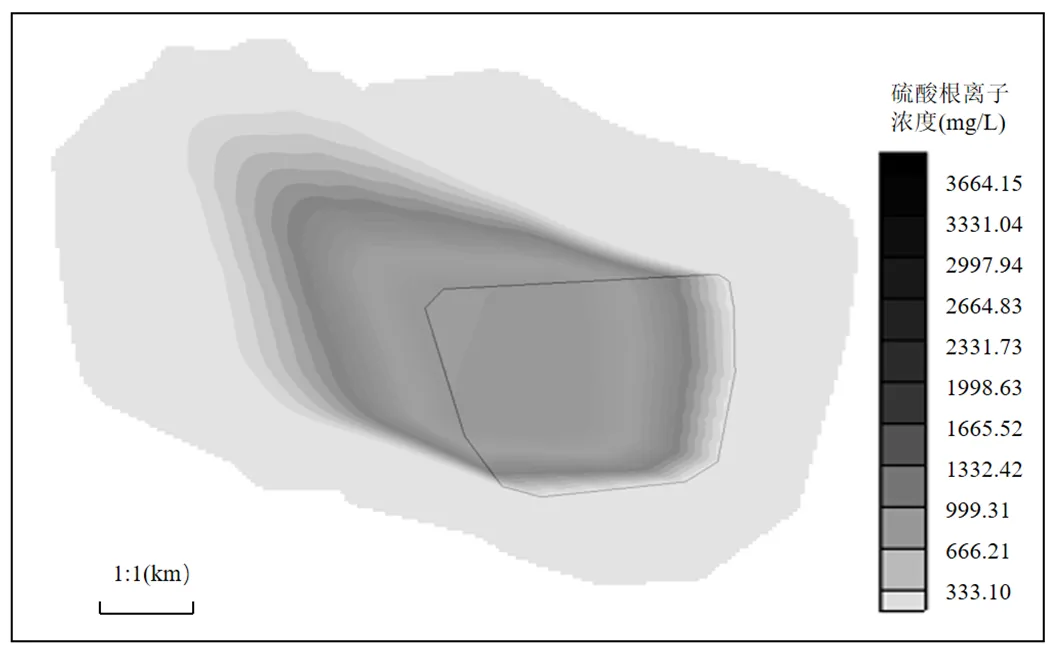
图3 污染物运移分布

2.2.2 灵敏度分析 筛选随机变量及方法对比本文将同时采用局部灵敏度分析和全局灵敏度分析,筛选出对模型影响较大的参数.

(1)局部灵敏度分析:对于污染场地的三口监测井,将孔隙度、渗透系数、降雨入渗系数以及纵向弥散度L这4个参数在波动范围内取均值输入到模拟模型中,得到一组标准输出值,后分别将各参数增加和减少10%,20%,且保证每次只变化一个参数,控制其他的参数不变,输入模型中得到污染物浓度的输出值,利用式(2)计算得到三口井各个参数的灵敏度,然后将三口井的参数灵敏度取均值,筛选出灵敏度最大的两个参数,结果如表3所示.

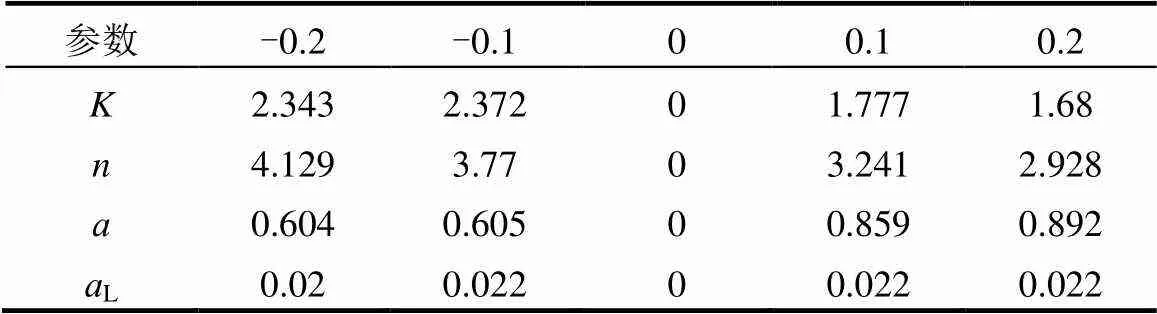
表3 灵敏度计算结果

根据3口监测井平均灵敏度分析示意图(图4),局部灵敏度分析法所筛选出的参数分别是孔隙度和渗透系数.

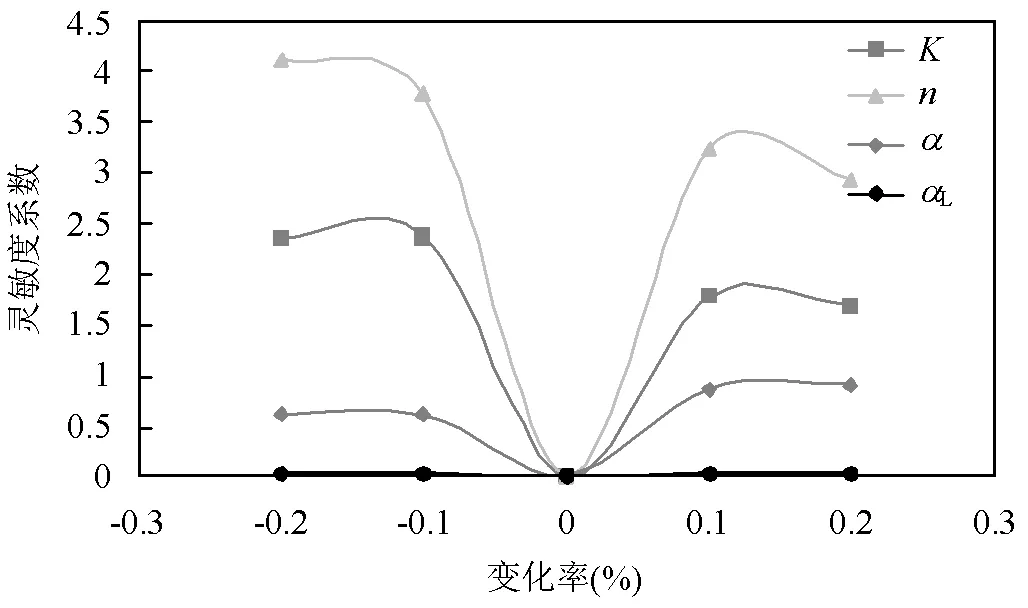
图4 三口监测井平均灵敏度分析示意

(2)全局灵敏度分析:同局部灵敏度分析选取同样的水文地质参数,进行全局灵敏度分析,每个参数分别有3种取值,即参数原值以及增加和减少10%的值.将4个参数进行组合,共有15种组合方式,如表4所示.

将表4的15组组合的参数变化后输入到模拟模型中,得到污染物的浓度值作为输出,为了方便不同参数灵敏度的比较,采用公式(3)、(4)、(5)计算得到各组在不同取值下的灵敏度,单组取多次平均值,即可得15组参数组合的全局灵敏度.

表4 参数组合方式

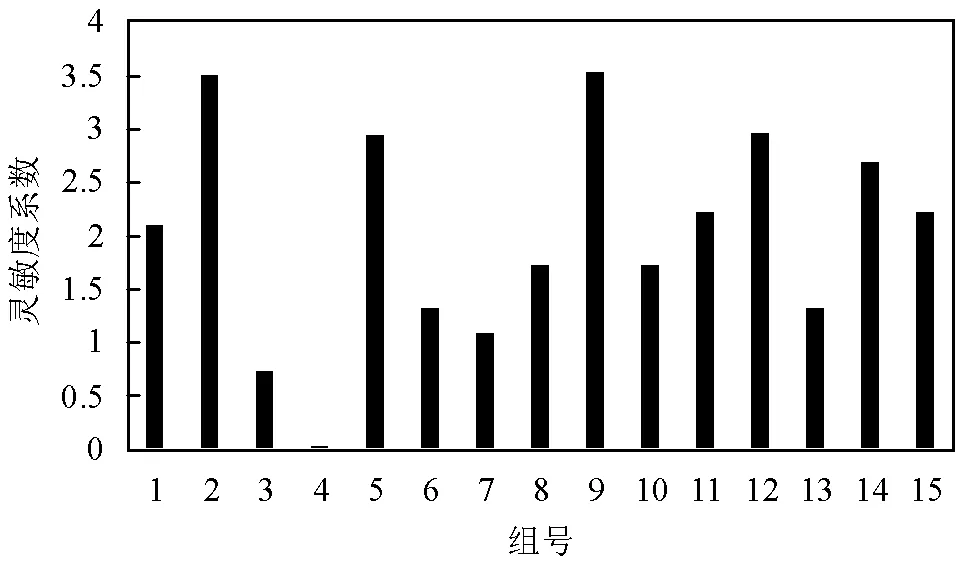
图5 参数全局灵敏度分析

如图5所示,灵敏度最高的两个参数分别是孔隙度和渗透系数该结果与局部灵敏度分析结果一致.但考虑不同参数的相互作用时,其结果存在差异,如图5中的组合6,在同时考虑孔隙度和渗透系数变化时,整体的灵敏度比二者单独的灵敏度要低,再如第15组,同时考虑四个参数同时变化所带来的影响,其结果并非是单参数影响的叠加,整体而言全局灵敏度分析更具实际意义.利用两种灵敏度分析方法(前者为试验方法,后者为检验方法)进行参数筛选其结果更具可靠性.

利用局部灵敏度分析和全局灵敏度分析共同筛选出对模型影响最大的两个参数:孔隙度和渗透系数将这两个参数作为随机变量,利用拉丁超立方抽样法进行抽样,其余的参数作为确定性变量.

2.2.3 拉丁超立方抽样 本文采用拉丁超立方抽样法分别在孔隙度、渗透系数以及三口抽水井抽水量的合理变化范围内进行抽样,其中考虑场地分区的差异性,对场地孔隙度及渗透系数进行2次抽样,分配给东西两个区域,后将所有抽样值随机组合,抽样的区间及服从的分布状态如表5所示.该抽样过程通过MATLAB软件实现,对上述参数分别抽取110组,随机组合得到输入样本集.

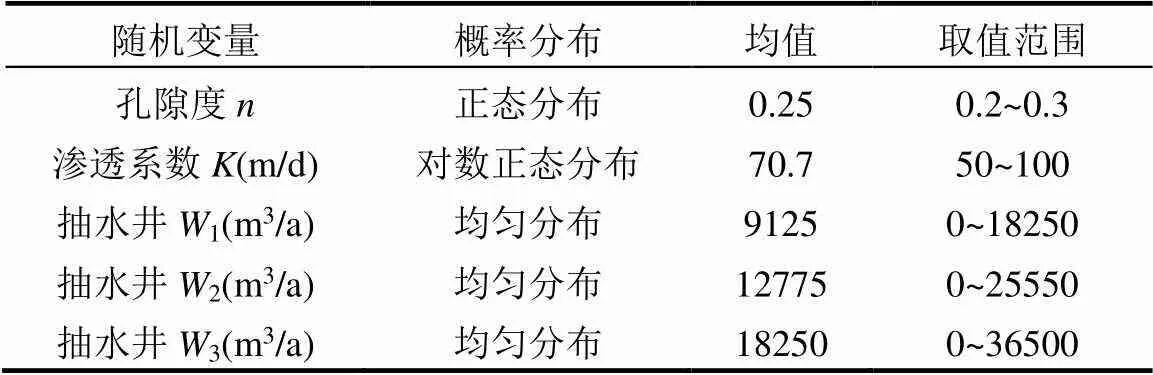
表5 参数概率分布及取值情况

2.2.4 建立替代模型 将上述2个分区的2个水文地质参数以及3口抽水井的抽水量共7维数据输入到地下水模拟模型中,运用GMS求解得到110组污染物的浓度即输出值.其中前100组作为训练样本建立替代模型,后10组作为检验样本检验替代模型的精度.

本文3口监测井分别采用BP神经网络(BPNN)方法、核极限学习机(KELM)方法、支持向量机(SVR)方法以及克里格(KRG)方法建立替代模型,选用确定性系数2以及平均相对百分比误差(MAPE)检验替代模型的精度,分别挑选出各井最适合的替代模型.

如下为评定精度指标的计算公式:

(1)确定性系数2:2的值越接近1则代表替代模型越精确.

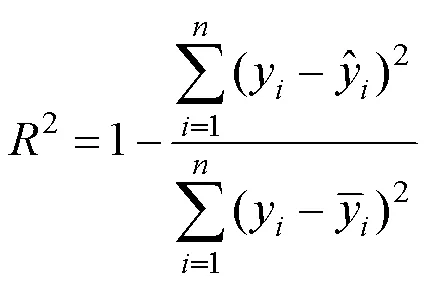
(2)平均相对百分比误差(MAPE):表示替代模型的输出结果同模拟模型输出结果的平均偏差.

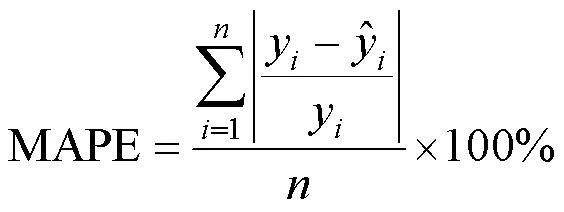
利用2和MAPE两个指标分别评定各个抽水井不同替代模型的精度,其结果如表6所示.

采用2进行精度评价时:通过计算可知抽水井W1最适用的替代模型是克里格替代模型,2达0.8214;抽水井W2最适用的替代模型是BP神经网络替代模型,2达0.9965;抽水井W3最适用的替代模型是克里格替代模型,2达0.9972.以2为评价指标为研究区3口井选定的替代模型依次为:克里格、BP神经网络及克里格替代模型.采用MAPE进行精度评价时:计算可知抽水井W1最适用的替代模型是核极限学习机替代模型,MAPE达10.49%;抽水井W2最适用的替代模型是BP神经网络替代模型,MAPE达4.12%;抽水井W3最适用的替代模型是克里格替代模型,MAPE达1.16%.以MAPE为评价指标为研究区3口井选定的替代模型依次为:核极限学习机、BP神经网络及克里格替代模型.

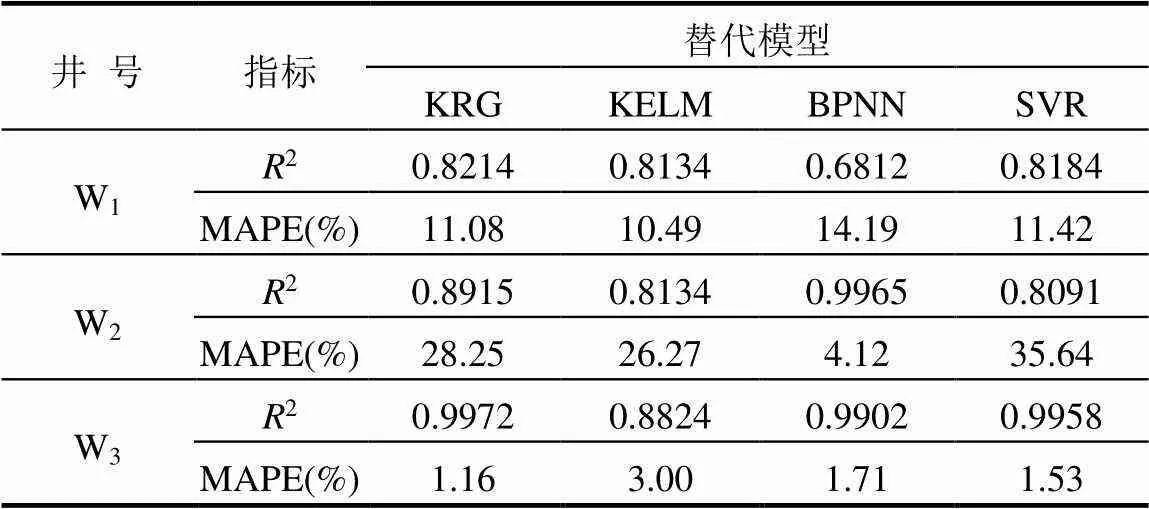
表6 三口井不同替代模型精度

2.2.5 替代模型精度检验 为验证3口井单独建立替代模型后的综合精度,本文将通过如下步骤进行分析:(1)场地的3口井同时应用一种方法建立替代模型,共4种方法,因此建立4组替代模型;(2)井1,2,3分别建立克里格、BP神经网络及克里格替代模型;(3)井1,2,3分别建立核极限学习机、BP神经网络及克里格替代模型;(4)以确定性系数2及平均相对百分比误差(MAPE)为评定指标评价上述各方法建立的替代模型的综合精度,结果如表7所示.

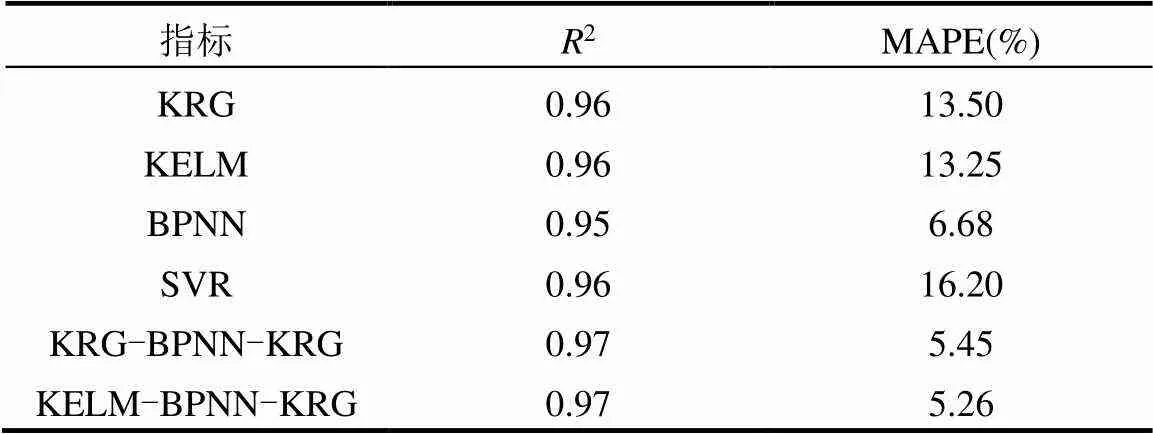
表7 不同类型替代模型精度

通过对比分析发现,单独建立各井的最优替代模型,其模拟精度有显著提升.单替代模型中MAPE最高的是BP神经网络替代模型,为6.68%,2最高的是克里格替代模型、支持向量机及核极限学习机替代模型,为0.96.依据单井最优建立的KRG-BPNN- KRG替代模型和KELM-BPNN-KRG替代模型的2接近,为0.97;前者MAPE为5.45%,后者MAPE为5.26%,整体的精度提升显著.但KELM-BPNN-KRG替代模型的MAPE值更低,因此选用KELM- BPNN-KRG替代模型进行后续的随机模拟.

2.2.6 蒙特卡罗随机模拟 本次研究采用蒙特卡罗法对研究场地的地下水污染进行随机模拟.第一步利用拉丁超立方抽样方法对前文叙述的7维数据进行抽样,得到1000组参数,然后将参数依次输入到KELM-BPNN-KRG替代模型中得到3口监测井污染物浓度输出值,最后对各井所对应的输出结果进行统计分析.

3 结果与讨论

3.1 统计与分析

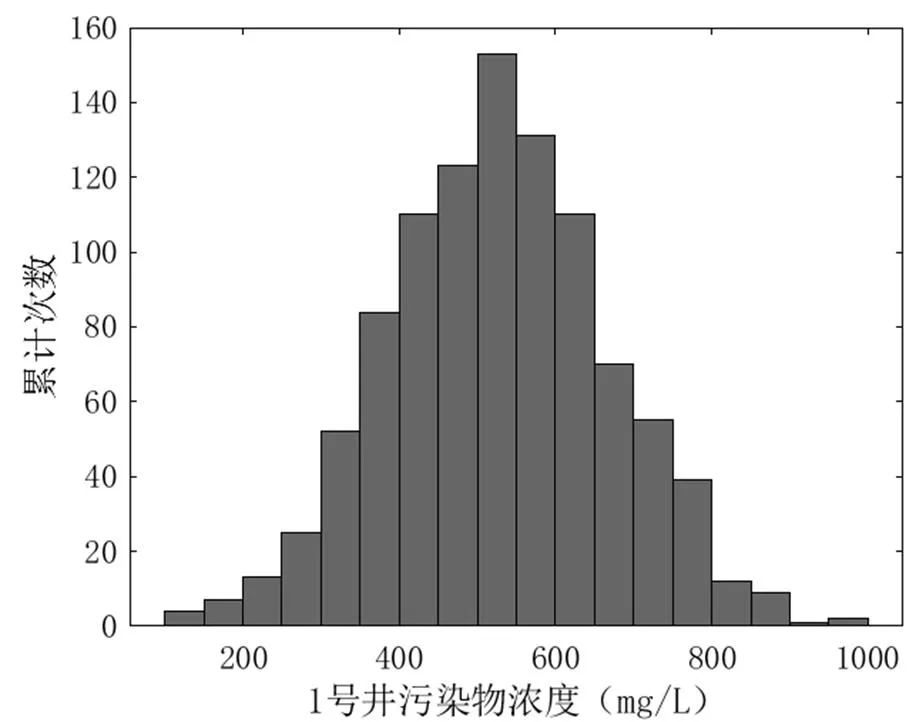
利用3口监测井的1000组数据绘制污染物浓度累计频次直方图并对其进行统计分析.如图6所示,1号井污染物浓度值集中在350～650mg/L,2号井污染物浓度值集中在50～270mg/L,3号井污染物浓度值集中在400～800mg/L.3口监测井的污染物浓度均值分别为528.26mg/L、167.83mg/L、594.90mg/L.其中3号井的污染最为严重,这是因为3号距离污染源较近且该井的抽水量最大,在一定程度上影响了污染物的运移;1号井同污染源的距离与3号井同污染源的距离接近,但其抽水量较少,其污染物的浓度比3号井污染物的浓度略低;2号井的污染物浓度最低,首先是因为其距污染源较远,其次3号井位于其东侧,3号井抽水量较大,使得后续污染物向西运移的浓度降低.

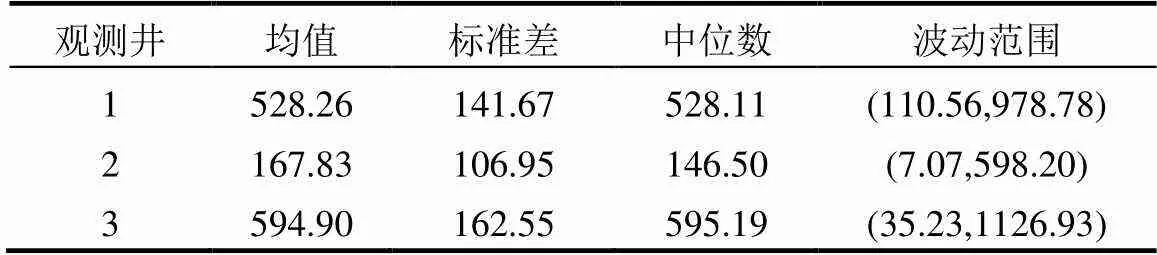
表8 三口监测井污染物输出值统计指标

3.2 区间估计

区间估计的主要目的是对未知参数真值范围在一定置信水平下进行估计,相比确定的结果,该种方法更具有实际意义.本文应用切比雪夫不等式,对污染场地3口监测井污染物浓度在一定置信水平下进行区间估计[5].

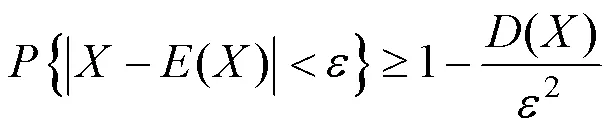
式中:()是各时段监测井污染物浓度均值;()为污染物浓度值的方差;是置信水平;为任意给定的正数.利用公式(20)计算得到三口监测井不同置信水平下污染物浓度的区间估计值,如表9所示,分析发现,置信水平越高,区间范围越大,根据实际的研究可以采取不同置信度下的污染物浓度范围.

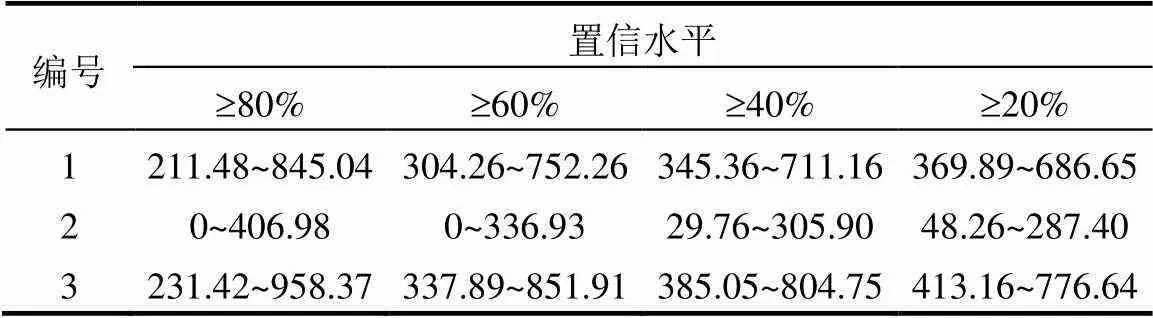
表9 各井不同置信水平污染物浓度值区间估计

3.3 风险评估

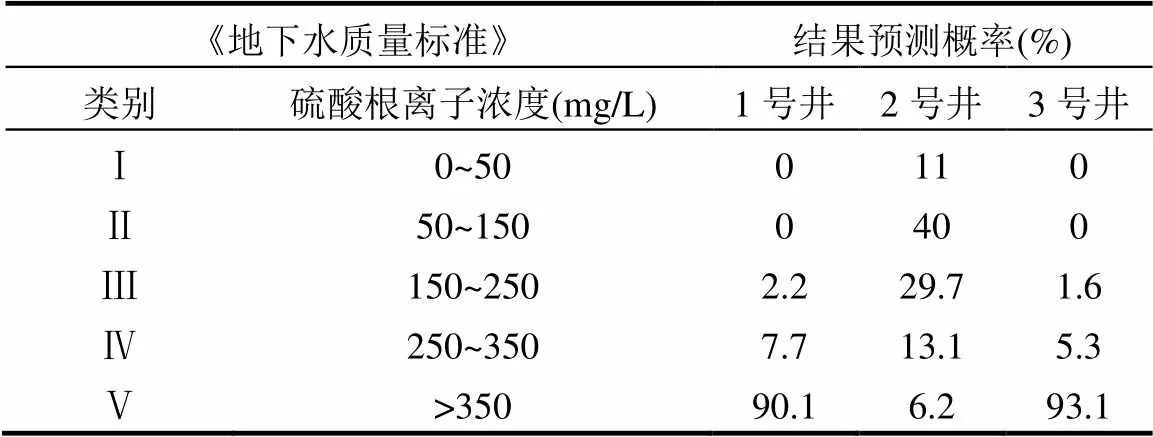
表10 污染物达标概率预测

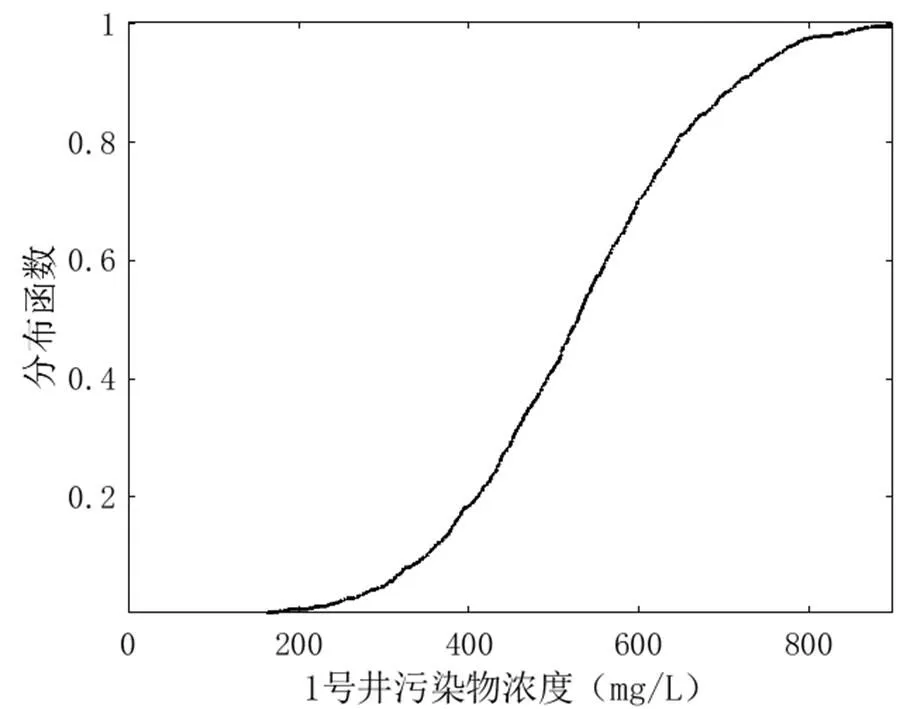
对1000组监测数据利用MATLAB软件绘制污染物浓度分布函数曲线,进行结果分析,其中纵坐标代表分布的概率,横坐标为浓度值(图7).考虑到污染场地的地理位置且有较多居民居住,参照《地下水质量标准》(GB/T 14848-2017)[19],利用概率分布曲线分析评定3口监测井中硫酸根离子达各级标准的概率,如表10所示.分析可知,硫酸根离子污染20a后,3口井达到Ⅰ类标准的概率依次为:0%、11%、0%;达到Ⅱ类标准的概率依次为:0%、40%、0%;达到Ⅲ类标准的概率依次为:2.2%、29.7%、1.6%;达到Ⅳ类标准的概率依次为:7.7%、13.1%、5.3%;达到Ⅴ类标准的概率依次为:90.1%、6.2%、93.1%.通过如上分析可知1号井和3号井污染严重,不易作为饮用水,2号井经适当处理可作为生活用水.

4 结论

4.1 利用局部灵敏度分析方法和全局灵敏度分析方法同时筛选出研究区灵敏度较大的两个参数:孔隙度和渗透系数,其中局部灵敏度分析方法作为试验方法,全局灵敏度方法作为验证方法,这使得筛选出的参数更加可靠且具有实际意义.

4.2 单独建立各井的最优替代模型,其模拟精度有显著提升.经过优选1,2,3号井的替代模型依次为:核极限学习机、BP神经网络及克里格替代模型,通过此方法既减少了反复调用模拟模型产生的巨大的计算负荷,又保持了较好的精度.

4.3 本文同时考虑了水文地质参数和源汇项的不确定性,对这两个因素应用蒙特卡罗方法对地下水数值模拟模型进行了不确定性分析,并估算了20年后各井水质达标情况.其中1号井和3号井达到Ⅴ类水的概率分别为90.1%和93.1%,污染严重.2号井达标Ⅲ类水的概率为80.7%,适当处理可作为生活用水.借此分析为地下水资源的利用以及污染防治提供合理依据.

5 展望

5.1 由于硫酸根离子在地下水环境中吸附和降解的作用较微弱,故本文只考虑了硫酸根离子保守迁移的情况,将在未来的研究中全面考虑该种情况.

5.2 一般来说,对非均质性越强的含水层建立替代模型,其精度会有一定程度的下降.本文根据水文地质条件实际情况,将研究区划分为两个渗透系数分区,非均质性较弱,在日后的研究中将探索高非均质性含水层建模任务.

[1] 王梓博,卢文喜,王 涵,等.某钼矿尾矿库地下水污染的随机模拟[J]. 中国环境科学, 2020,40(5):2124-2131.

Wang Z B, Lu W X, Wang H, et al.Stochastic simulation of groundwater pollution in a molybdenum tailings reservoir [J]. China Environmental Science, 2020,40(5):2124-2131.

[2] Li F, Zhu J, Deng X, et al. Assessment and Uncertainty Analysis of Groundwater Risk Lifawem [J]. Environmental Research, 2018,160: 140-151.

[3] 常振波,卢文喜,辛 欣,等.基于灵敏度分析和替代模型的地下水污染风险评价方法[J]. 中国环境科学, 2017,37(1):167-173.

Chang Z B, Lu W X, Xin X, et al. Groundwater pollution risk assessment method based on sensitivity analysis and surrogate model [J]. China Environmental Science, 2017,37(1):167-173.

[4] 李久辉,卢文喜,辛 欣,等.考虑边界条件不确定性的地下水污染风险分析[J]. 中国环境科学, 2018,38(6):2167-2174.

Li J H, Lu W X, Xin X, et al. Groundwater pollution risk analysis considering uncertainty of boundary conditions [J]. China Environmental Science, 2018,38(6):2167-2174.

[5] 袁 乾,卢文喜,范 越,等.基于替代模型的煤矸石堆地下水污染随机模拟[J]. 中国环境科学, 2019,39(6):2444-2451.

Yuan Q, Lu W X, Fan Y, et al. Stochastic simulation of groundwater pollution in gangue dump based on surrogate model [J]. China Environmental Science, 2019,39(6):2444-2451.

[6] 高鑫宇,曾献奎,吴吉春.基于改进稀疏网格替代模拟的地下水DNAPLs运移不确定性分析[J]. 水文地质工程地质, 2020,47(1):1-10.

Gao X Y, Zeng X K, Wu J C. Uncertainty analysis of groundwater DNAPLs migration based on improved sparse grid instead of simulation [J]. Hydrogeology Engineering Geology, 2020,47(1):1-10.

[7] 侯泽宇,王 宇,卢文喜.地下水DNAPLs污染修复多相流模拟的替代模型[J]. 中国环境科学, 2019,39(7):2913-2920.

Hou Z Y, Wang Y, Lu W X. An surrogate model for simulation of multiphase flow for groundwater DNA PLs contamination remediation [J]. China Environmental Science, 2019,39(7):2913-2920.

[8] 葛渊博,卢文喜,王梓博,等.基于BP神经网络替代模型的地下水污染随机模拟[J]. 中国农村水利水电, 2022,(3):107-113,119.

Ge Y B, Lu W X, Wang Z B, et al. Stochastic simulation of groundwater pollution based on BP neural network surrogate model [J]. Rural Water Resources and Hydropower in China, 2022,(3):107-113,119.

[9] 王 涵,卢文喜,李久辉,等.地下水DNAPLs污染多相流的随机模拟及其不确定性分析[J]. 中国环境科学, 2018,38(7):2572-2579.

Wang H, Lu W X, Li J H, et al. Stochasticsimulation of multiphase flow contaminated by groundwater DNAPLs and analysis of uncertainty [J]. China Environmental Science, 2018,38(7):2572-2579.

[10] Luo J, Lu W. Sobol'sensitivity analysis of NAPL-contaminated aquifer remediation process based on multiple surrogates [J]. Computers & Geosciences, 2014,67:110-116.

[11] SOBOL'I M. Sensitivity estimates for nonlinear mathematicalmodels [J]. Mathematical Modelling Computer Experiments, 1993,1(4):407-414.

[12] 王浩昌,杜鹏飞,赵冬泉,等.城市降雨径流模型参数全局灵敏度分析[J]. 中国环境科学, 2008,(8):725-729.

Wang H C, Du P F, Zhao D Q, et al. Global sensitivity analysis of urban rainfall-runoff model parameters [J]. China Environmental Science, 2008,(8):725-729.

[13] 束龙仓,王茂枚,刘瑞国,等.地下水数值模拟中的参数灵敏度分析[J]. 河海大学学报(自然科学版), 2007,(5):491-495.

Shu L C, Wang M M, Liu R G, et al. Sensitivity analysis of parameters in groundwater numerical simulation [J]. Journal of Hohai University (Natural Science Edition), 2007,(5):491-495.

[14] 刘 波,金爱兵,高永涛,等.基于Morris法的单裂隙岩体温度场参数灵敏度分析[J]. 采矿与安全工程学报, 2016,33(1):152-157.

Liu B, Jin A B, Gao Y T, et al. Sensitivity analysis of temperature field parameters of single fractured rock mass based on Morris method [J]. Journal of Mining and Safety Engineering, 2016,33(1):152-157.

[15] 贾顺卿,卢文喜,李久辉,等.基于U-D分解卡尔曼滤波地下水污染源溯源辨识[J]. 中国环境科学, 2021,41(2):713-719.

Jia S Q, Lu W X, Li J H, et al. Inverseidentification of groundwater pollution source based on U-D decomposition Kalman filter [J]. China Environmental Science , 2021,41(2):713-719.

[16] 李 萍,曾令可,税安泽,等.基于MATLAB的BP神经网络预测系统的设计[J]. 计算机应用与软件, 2008,(4):149-150,184.

Li P, Zeng L K, Shui A Z, et al. Design of BP neural network prediction system based on MATLAB [J]. Computer Applications and Software, 2008,(4):149-150,184.

[17] 潘紫东,卢文喜,范 越,等.基于模拟-优化方法的地下水污染源溯源辨识[J]. 中国环境科学, 2020,40(4):1698-1705.

Pan Z D, Lu W X, Fan Y, et al. Inverseidentification of groundwater pollution sources based on simulation-optimization method [J]. China Environmental Science, 2020,40(4):1698-1705.

[18] Wu S, Wang Y, Cheng S . Extreme learning machine based wind speed estimation and sensorless control for wind turbine power generation system [J]. Neurocomputing, 2013,102(FEB.15):163-175.

[19] GB/T 14848-2017 地下水质量标准[S].

GB/T 14848-2017 Groundwater quality standard [S].

Uncertainty analysis of groundwater pollution simulation model.

LUO Cheng-ming1,2, LU Wen-xi1,2*, WANG Zi-bo1,2, CHANG Zhen-bo1,2

(1.Key Laboratory of Groundwater Resources and Environmental, Ministry of Education, Jilin University, Changchun 130012, China；2.College of New Energy and Environment, Jilin University, Changchun 130012, China)., 2022,42(7)：3224～3233

In order to simultaneously analyze the effect of source and sink items and hydrogeological parameters uncertainty on the output of groundwater pollution numerical simulation model, a gangue dump site in Fushun City was taken as an example to study. Firstly, the groundwater pollution numerical simulation model of the site was established with sulfate ion as the simulation factor. Then, local sensitivity analysis and global sensitivity analysis were used to analyze the sensitivity of the simulation model parameters, and the results of thetwowere compared. Finally, two parameters that have a great impact on the model output were selected as the random parameters of the model.In order to reduce the calculation load caused by repeatedly calling the simulation model, four methods of Kriging(KRG), kernel extremelearning machine(KELM), support vector machine(SVM) and BP neural network (BPNN) were used to establish the surrogate model of the simulation model for three observation wells respectively. According to the fitting effect of the four surrogate models in different wells, a surrogate model with the best performance was selected for each well, Monte Carlo stochastic simulation was completed by using the optimized surrogate model. Finally, statistical analysis and risk assessment were carried out on the results of random simulation. The results show that when the confidence was 80%, the confidence intervals of the concentration values of the well 1,2,3 were 211.48～845.04mg/L, 0～406.98mg/L, 231.42～958.37mg/L. In addition, according to the groundwater quality standard and the pollutant concentration distribution function curve of each well, the probability that the water quality of well 1 and well 3 met the class V water standard was 90.1% and 93.1% respectively, and the probability that well 2 met the class III water standard was 80.7%, so as to provide a reasonable basis for groundwater resource management and pollution prevention and control.

stochastics simulation of groundwater pollution；sensitivity analysis；surrogate model；uncertainty analysis；risk assessment

X523 文献识别码：A

1000-6923(2022)07-3224-10

罗成明(2000-),男,四川南充人,吉林大学硕士研究生,主要从事地下水数值模拟方面研究.

2021-11-29

国家自然科学基金资助项目(41972252);国家重点研发计划(2018YFC1800405)

* 责任作者, 教授, luwenxi@jlu.edu.cn