二维范德瓦耳斯半导体莫尔超晶格实验研究进展*

李听昕

1) (上海交通大学物理与天文学院,沈阳国家材料研究中心上海交通大学分部,人工结构及量子调控教育部重点实验室,上海 200240)

2) (上海交通大学李政道研究所,上海 201210)

在二维范德瓦耳斯材料中,可以通过转角及晶格失配构造周期性的莫尔超晶格.自从实验上在“魔角”石墨烯系统中观察到关联绝缘体态和超导电性以来,利用各种二维范德瓦耳斯材料构造莫尔超晶格并研究其中的新奇量子物态成为了凝聚态物理研究的热点和前沿问题.本文主要综述了最近几年在二维半导体过渡金属硫族化合物莫尔超晶格系统中的相关实验进展.在该系统中实现电子“平带”不依赖于特定魔角,实验上,一系列的关联电子物态和拓扑电子物态被相继发现和证实.进一步的理论和实验研究有望在该系统中揭示更多的受电子关联作用和拓扑物理共同支配的新奇量子物态.

1 引言

通过构造人工周期性结构实现对晶体能带及电子态的有效调控长期以来都是凝聚态物理研究中的一个重要方向,最早可以追溯到Esaki 和Tsu[1]有关半导体一维超晶格的工作.在传统材料中,构造人工电子超晶格通常采用的是高质量的材料生长技术结合先进的微纳米加工手段[2].而二维范德瓦耳斯材料区别于传统材料的一个突出特点是其层间耦合较弱,因此可以不受晶格匹配的限制而任意组合堆垛形成异质结构,这也使得通过转角等方式构造莫尔超晶格结构成为可能.事实证明,二维范德瓦耳斯材料莫尔超晶格为人们研究和调控关联电子态以及拓扑电子态提供了一个高度可控的全新平台.实验上,自2018 年美国麻省理工学院的Jarillo-Herrero 课题组在“魔角”石墨烯系统的“平带”中观测到关联绝缘体[3]和超导电性[4]以来,一系列基于二维范德瓦耳斯材料莫尔超晶格系统的关联电子态和拓扑电子态被人们发现和证实[5−65],而且这些量子物态可以有效地被电场、磁场、载流子浓度、转角、压力等参量调控,吸引了大批科学家的目光.

电子的“平带”是一个相对的概念,其核心是平带中的电子-电子库仑相互作用能与电子的动能(带宽)可比,从而使得库仑相互作用对系统的物理性质起到支配作用[44,66],此时系统不再能被“单电子”近似下的理论描述,而是需要使用考虑关联电子效应的量子多体理论处理.实验上,强关联电子系统一次又一次地呈现出完全出人意料的奇妙量子物态,著名的例子包括分数量子霍尔效应[67]、高温超导[68]等;与此同时,如何全面地理解这些强关联电子物态也在理论上对人们提出了一个又一个挑战,实验和理论相辅相成极大地推动了凝聚态物理学的发展,使得强关联电子系统的研究成为了凝聚态物理研究的主旋律之一.那么在二维材料莫尔超晶格中实现“平带”的关键是什么呢? 如果考虑某种材料具有简单的抛物线型能带结构,其晶格常数为a,通过转角等方式构造得到的莫尔超晶格的晶格常数为λ,则由于莫尔周期势导致的能带“折叠”效应,新的布里渊区的顶点为,那么最简单的估算可认为其莫尔子带带宽w为,其中m*为材料的电子有效质量;至于相互作用能,最简单的估计可以认为当每个莫尔格点上有一个电子时,其能量尺度应在量级,其中ε为周围介电环境的介电常数.如果希望电子-电子相互作用能大于电子的动能,则需要,即λ和m*的乘积比较大[44].另一方面,由于λ的值可以由转角等方式控制,因此理论上对于任何二维半导体或半金属范德瓦耳斯材料,当转角小于某一阈值(即λ大于某一阈值)时都有可能实现“平带”,并可以通过栅极来控制“平带”中的载流子填充数.

然而,以上的估计相较于真实材料系统而言还是过于简单了,比如在转角石墨烯系统中,2011 年美国德州大学奥斯汀分校的MacDonald 课题组[69]通过理论研究发现,由于石墨烯狄拉克点附近的能带色散关系为线性,故其“平带”仅出现在一系列特定角度,并将这些角度称之为“魔角”.另外,上述有关相互作用能的估算也过于简单,实际上,相互作用能除了与λ的大小有关以外,更为重要的是形成莫尔超晶格的材料之间是否能有效耦合,即是否能形成足够强的莫尔周期势.比如,石墨烯/氮化硼系统[70−72]与魔角双层石墨烯系统具有相似的莫尔超晶格常数λ(约13—14 nm),但由于氮化硼与石墨烯的能带不能有效耦合,因此不能在零磁场条件下实现“平带”和强关联电子态.最后,虽然原则上λ越大越容易实现电子平带,但λ同时还决定了莫尔子带能够填充的载流子浓度,真实材料中不可避免地有杂质和缺陷存在,而为了观测到系统本征的物理效应,一般需要莫尔子带的载流子填充浓度远大于杂质、缺陷等的浓度;此外,获得较大的λ通常意味着需要很小的转角,而系统的晶格弛豫效应一般在小转角情况下比较显著[73−75],这使得实验上当λ较大时,难以获得均匀的莫尔超晶格结构.

综合以上因素,除了石墨烯以外,二维半导体过渡金属硫族化合物(TMDc)无疑是构造莫尔超晶格的理想材料体系之一.首先,二维半导体过渡金属硫族化合物的能带结构简单、能带有效质量大(约0.5m0),因此容易实现“平带”物理.2018 年MacDonald 课题组[76]的理论计算结果表明,TMDc莫尔超晶格实现“平带”不需要特定“魔角”,只要转角不是太大(小于3.5°,即λ约大于6 nm)的情况下,第一莫尔子带均为“平带”.其次,二维半导体莫尔超晶格的莫尔周期势强,带宽及相互作用能等参数高度可调,理论上可作为Hubbard 模型[76−78]、Kane-Mele 模型[79−81]、Kondo 晶格模型[82]等的量子模拟器,为研究、模拟和调控凝聚态体系中的强关联电子态和拓扑电子态提供了理想的材料平台.此外,通过机械剥离获得的二维半导体TMDc 晶体具有很高的质量,一个有力的实验证据是最近在单层WSe2中通过量子电容测量观测到的一系列分数量子霍尔效应态[83],这为在二维半导体TMDc莫尔超晶格中探索和研究新颖的量子物态奠定了材料基础.

2 TMDc 莫尔超晶格中的关联电子态研究

2.1 单层半导体TMDc 材料的基本性质

与由单原子层构成的石墨烯或者单层六角硼氮略有不同,单层TMDc 材料由三层原子构成(如图1(a)所示),其中间层为过渡金属原子(W,Mo等),其余两层为硫族元素原子(S,Se,Te 等),根据具体晶格结构的不同TMDc 材料还可分为2H,1T,1T'等相[84].其中2H相的单层TMDc 具有与单层石墨烯类似的六角蜂窝状结构(如图1(b)所示),但由于单层TMDc 不具备中心反演对称性,因此在K和K'谷打开了能隙(常见2H-TMDc 材料的能隙在1—2 eV 左右),故其能带结构为半导体而非半金属(图1(c)).实验上通过输运测量量子振荡得到的单层TMDc 材料的有效质量约为0.4m0—0.8m0[85−87].一方面,由于过渡金属原子具有很强的Ising 型自旋-s 轨道耦合作用[88],因此在某一个能谷内,自旋简并度被打开,其价带的自旋劈裂能量可达300 meV,而导带的自旋劈裂能量一般为几到几十meV.另一方面,由于系统仍保持有时间反演对称性,故K和K'谷自旋劈裂能带的自旋方向是相反的,即呈现所谓的“谷-自旋锁定”效应[84].因此,在系统的费米能较低的情况下,系统的简并度为2.有关二维半导体TMDc 最早的研究始于其独特的光学性质;2010 年,加州伯克利的Wang 课题组[89]和美国哥伦比亚大学的Heinz 课题组[90]发现单层的MoS2为直接带隙半导体,表现出很强的光吸收和荧光发射;而两层及以上MoS2由于层间耦合的作用表现为间接带隙半导体.

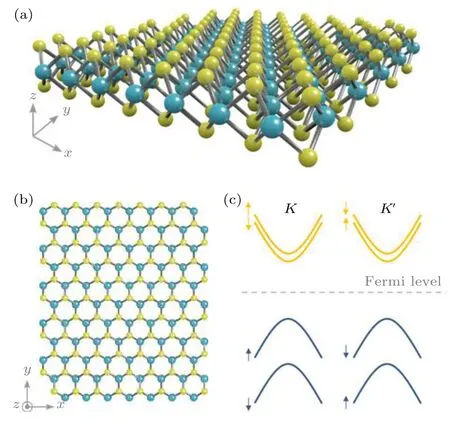
图1 过渡金属硫族化合物 (a),(b) 2H 相TMDc 的结构示意图,其中青色代表过渡金属原子,黄色代表硫族元素原子;(c) 2H 相TMDc 的能带结构示意图Fig.1.Transition metal dichalcogenides:(a),(b) Schematic illustrations of 2H phase TMDc,where cyan balls denote transition metal atoms and yellow balls denote chalcogenide atoms;(c) schematic band structures of 2H TMDc.

2.2 TMDc 莫尔超晶格

由于TMDc 包括多种物理性质类似的材料,因此在构造莫尔超晶格时,除了采用同种材料转角的办法来构造TMDc 莫尔超晶格同质结,也可以利用不同TMDc 材料的晶格失配(或转角)来构造TMDc 莫尔超晶格异质结.得到的莫尔超晶格的晶格常数λ为

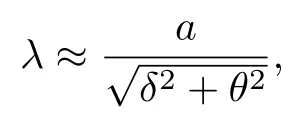
其中,δ为两种TMDc 材料晶格失配的百分比,θ为转角.相比于莫尔超晶格同质结,由晶格失配构造的TMDc 莫尔超晶格异质结的λ对θ的变化不敏感,因此容易获得较为均匀的莫尔超晶格器件.图2 给出的是以转角MoS2为例(其中图2(a)为3.5°转角,图2(e)为56.5°转角)构造的莫尔超晶格同质结的示意图[91],图中不同颜色的虚线圈代表堆垛方式不同的高对称性点,可见每一种高对称性点构成了一套三角格子的超晶格.与转角石墨烯系统不同的是,由于TMDc 材料原本的六角晶格包含两种不同原子,仅具有三重旋转对称性,因此当用两层TMDc 构造莫尔超晶格时,在接近0°转角和接近60°转角的情况下,会存在有λ相同但堆垛方式截然不同的两种莫尔超晶格,如图2(b)—图2(c)和图2(f)—图2(h)所示,在文献中一般被称作AA 堆垛(接近0°,120°,240°转角)和AB 堆垛(接近60°,180°,300°转角)的TMDc 莫尔超晶格.莫尔超晶格中的另一个重要参数为莫尔超晶格的填充因子v,其含义为每个莫尔超晶格元胞中填充的电子(空穴)数目.可见,如果系统的简并度为g,则当v=g时,第一个莫尔子带被填满.

图2 转角MoS2 莫尔超晶格[91].AA 堆垛(3.5°转角,(a)—(d))和AB 堆垛的(56.5°转角,(e)—(h))MoS2 莫尔超晶格的示意图及高对称性点的堆垛示意图Fig.2.Twisted MoS2 moiré superlattices [91]: Schematics plots of AA-stacked (3.5° twisted,(a)–(d)) and AB-stacked(56.5° twisted,(e)–(h)) MoS2 moiré superlattices,the highsymmetry stackings are highlighted by circles.

在较早的扫描隧道显微镜实验研究中[92,93],美国德州大学奥斯汀分校的Shih 等课题组通过原位生长沿晶相对准的MoS2/WSe2,已经观察到了晶格周期约为8 nm 的莫尔超晶格结构,并通过扫描隧道谱学测量证实了其中可以形成较强的莫尔周期势场.2017 年,MacDonald 课题组[94]和香港大学的Yao 课题组[95]从理论上提出在TMDc莫尔超晶格中,由于有效的莫尔周期势的存在,使得在TMDc 莫尔超晶格中可以出现一系列不同于单层TMDc 激子态的莫尔激子态;2019 年,美国加州大学伯克利分校Wang 课题组[42]、华盛顿大学Xu 课题组[40]、德州大学奥斯汀分校Li 课题组[41]和英国谢菲尔德大学Tartakovskii 课题组[43]同时独立地报道了在WSe2/WS2,WSe2/MoSe2和MoSe2/WS2莫尔超晶格中莫尔激子态的实验观测结果.

2.3 TMDc 莫尔超晶格中关联电子态的实验研究

引言部分提到,与“魔角”石墨烯系统类似,莫尔周期势的存在可以使TMDc 莫尔超晶格中出现“平带”,从而有望实现一系列关联电子态和拓扑电子态.理论上,MacDonald 课题组[76]在2018 年首先提出在TMDc 莫尔超晶格异质结中,由于其Wannier 轨道主要局域在莫尔超晶格的某一种高对称性堆垛点上,故其“平带”中的物理在理论上可以用三角格点上的单带Hubbard 模型描述,且模型参数可由转角等参数调控,原则上可以作为一种新型的Hubbard 模型量子模拟器.Hubbard 模型[96]是强关联多体物理中的基本模型,形式简单却具有重要的物理意义,与磁性、关联绝缘体、高温超导体等诸多重要的强关联现象的物理机理密切相关[97].尽管最简单的Hubbard 模型仅包括两项,即格点间的跳跃能t(与带宽w相关)和电子双占据同一格点时的库仑排斥能U,但其也仅在一维情况下可以精确求解,因此在实验上找到能够模拟Hubbard 模型的物理系统对于理解一系列强关联物理现象具有重要的意义,目前最具代表性的Hubbard 模型量子模拟器为冷原子系统[98,99].

实验上,2020 年加州大学伯克利分校Wang课题组[44]、美国康奈尔大学Shan 和Mak 课题组[45]同时报道了在沿晶相对准的WSe2/WS2莫尔超晶格中关联电子效应的研究工作.WSe2与WS2存在约4%的晶格失配,因此将两者沿晶相对准后可以形成λ约为8 nm 的莫尔超晶格.单层WSe2与单层WS2组合的能带为第二型能带排列(type II or staggered alignment),其价带顶在WSe2层(价带带阶约为600 meV)[100],导带底在WS2层(导带带阶约为350 meV)[100];形成莫尔超晶格后,莫尔周期势使原本的能带发生“折叠”,形成一系列莫尔子带,如图3(c)所示[45].Wang 课题组[44]发展了一套基于光学探测来测量样品量子电容和电阻的办法,并发现当WSe2/WS2价带的第一莫尔子带半填充时(考虑到系统的简并度为2,故对应于莫尔超晶格填充因子v=1),出现了由电子-电子相互作用导致的Mott 绝缘体态,这对应于Hubbard 模型中U≫t的情况;而当莫尔子带处于v=1/3 和2/3 的分数填充时,也存在有关联绝缘体态,称之为广义的Wigner 晶态,这对应于扩展的Hubbard模型中U,V≫t的情况,其中V为格点间空穴的库仑排斥能,部分实验数据见图3(a)和图3(b).Shan 和Mak 课题组[45]通过电输运和光学测量也发现,在v=1 时存在Mott 绝缘体态(图3(c)),并通过磁光测量系统地研究了外加磁场下系统莫尔激子态的等效g因子随v的变化,实验发现WSe2/WS2莫尔超晶格体系的Mott 绝缘体态表现出反铁磁的Curie-Weiss 行为(图3(e)).

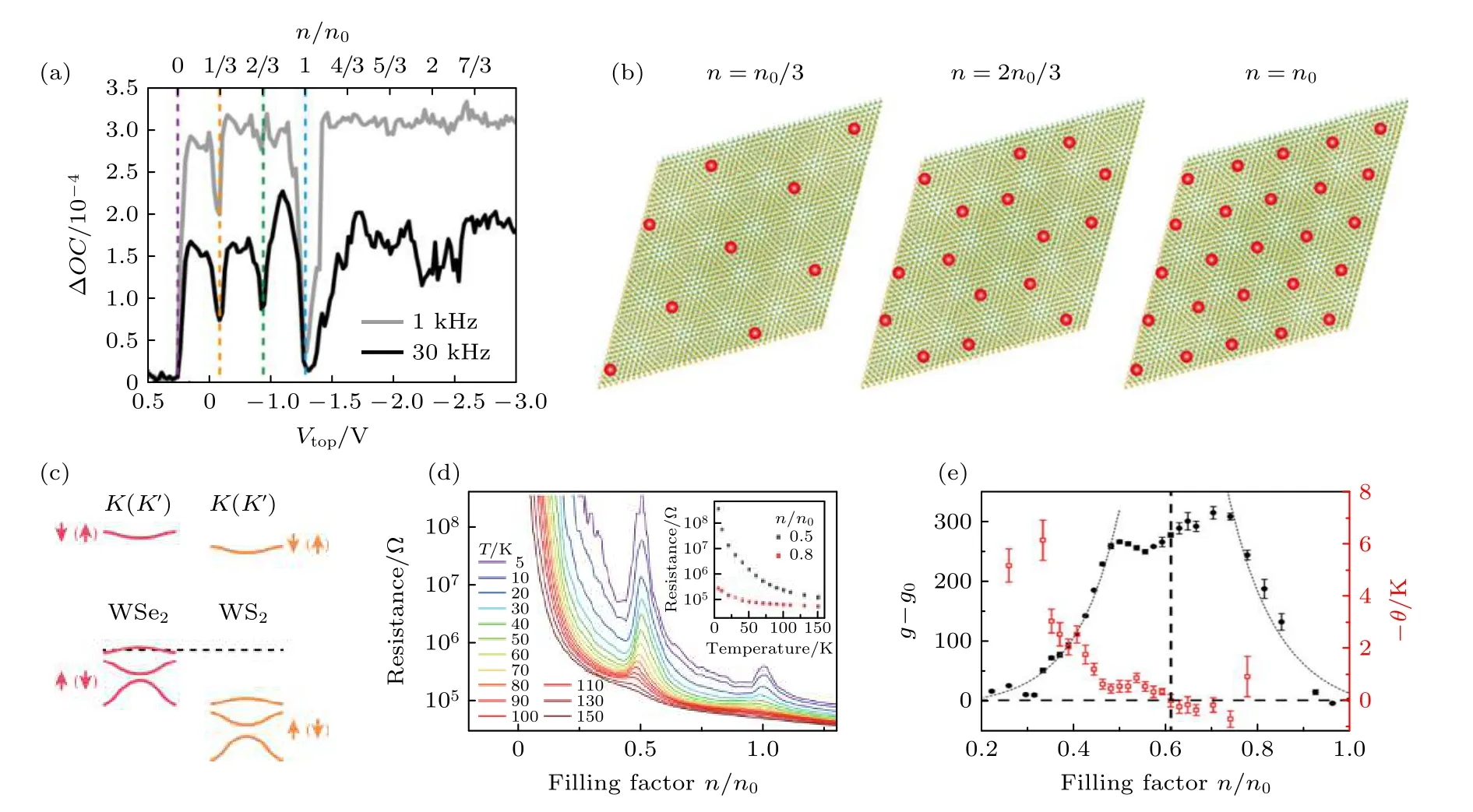
图3 WSe2/WS2 莫尔超晶格中的关联电子态 (a) 基于光学探测得到的WSe2/WS2 莫尔超晶格样品的量子电容信号[44];(b)莫尔超晶格Mott 绝缘体和广义的Wigner 晶态示意图[44];(c) WSe2/WS2 莫尔超晶格能带结构示意图[45];(d) 不同温度下通过两端输运测量得到的WSe2/WS2 莫尔超晶格的电阻随填充因子的变化[45];(e) 通过磁光测量得到的等效g 因子和Wiess 温度随v 的变化[45].值得指出的是,图(a)中横轴n/n0 的含义即为莫尔超晶格填充因子v;而图(d),(e)中横轴n/n0 的含义为莫尔子带填充因子,即为2vFig.3.Correlated states in WSe2/WS2 moiré superlattices:(a) Quantum capacitance signals detected by optical probe in WSe2/WS2 moiré superlattices [44];(b) schematic illustrations of Mott insulator and generalized Wigner crystal states [44];(c) schematic band alignment of the WSe2/WS2 moiré superlattice;(d) temperature dependence of two-terminal resistance of WSe2/WS2 moiré superlattices versus moiré filling factors [45];(e) g factors and Wiess temperatures versus moiré filling factors obtained by magneto-optical measurements [45].The top x-axis n/n0 of panel (a) equals to the moiré filling factor v,whereas the x-axis n/n0 of panels (d) and (e)represents the moiré mini band filling factor,which equals to 2v.

在随后的实验中[46],Shan 和Mak 课题组发展出一套灵敏的“激子探测”办法,在WSe2/WS2莫尔超晶格系统中观测到了更多的广义的Wigner 晶态(v=1/2,2/5,3/5,1/4,3/4,1/7,6/7),显示了该系统中长程(尺度在一个至几个λ)电子-电子相互作用仍起着重要的作用.通过光学各向异性测量,Shan 和Mak 课题组[47]还证实了WSe2/WS2莫尔超晶格中v=1/2,2/5,3/5 态是由于相互作用导致的旋转对称性自发破缺的电子条纹态.最近,Wang 课题组[48]通过采用一层石墨烯层作为电荷探测层的办法,成功利用扫描隧道显微镜观察到了WSe2/WS2莫尔超晶格中广义Wigner 晶态的晶格结构.此外,人们还通过微波阻抗[50,51]、量子电容[52]、反射及荧光光谱[49,53−56]、扫描隧道谱[57−60]、角分辨光电子能谱[61]等多种测量方法从各个角度研究了WSe2/WS2莫尔超晶格或类似的异质结莫尔超晶格中的Mott 绝缘体态、广义的Wigner 晶态及其他电子关联效应.

上述实验工作充分展现了TMDc 莫尔超晶格在U≫t情况下呈现出的丰富的电子关联效应.另一个有意思的物理问题是减小U/t的比值使系统发生Mott 绝缘体到金属态的相变(简称Mott相变),在多数材料系统中,这一相变是一阶相变并伴随着磁性相变、结构相变等过程[101].而不伴随任何形式对称性破缺的连续Mott 相变过程及其相变点附近的物理性质,仍是凝聚态物理中的一个备受关注的问题[102−105].比如,理论上预言[102,103]对于三角晶格,由于阻挫的存在,很可能会发生连续Mott 相变,且相变点附近会存在有量子自旋液体态.TMDc 莫尔超晶格系统恰为三角晶格上的强关联系统,那么有没有什么办法可以调节尤其是连续地原位调节系统的U/t比值呢? 2021 年,美国哥伦比亚大学Dean 课题组[62]、康奈尔大学Shan 和Mak 课题组[63]的实验工作展示了在合适的TMDc莫尔超晶格系统中,通过栅极施加电场的方法可以有效地调节系统的U/t比值,从而能够实现由带宽调节的Mott 绝缘体-金属相变.其中,Dean 课题组采用的是转角WSe2莫尔同质结超晶格,在先前的实验中[64],该课题组报道了有关转角WSe2中关联绝缘体态和初步超导态迹象的实验观测,并通过理论计算表明该系统中通过外加电场调节两层WSe2相对的能带位置,可以实现U/t比值的调节.在最近的实验中,Dean 课题组[62]详细地研究了带宽调节和载流子浓度调节的Mott 绝缘体-金属相变区域的输运性质,发现其相变临界区内存在明显的不符合费米液体行为的金属态,部分实验数据如图4(a)和图4(b)所示.Shan 和Mak 课题组[63]则研究了AA 堆垛的MoTe2/WSe2莫尔异质结价带中莫尔子带的输运性质和光谱学性质,在零电场情况下,MoTe2与WSe2材料的价带带阶的能量约相差200 meV[100],通过外加电场可以使得两者的带阶进一步接近,从而显著改变层间耦合的强度进而影响体系U/t的比值.实验上,该课题组观察到了由外加电场调控的连续Mott 相变(图4(c)—图4(e)),并发现其相变附近的电阻测量结果符合量子相变临界区的标度行为.此外,当保持莫尔子带半满的情况下(v=1),在靠近Mott 相变点的金属态区域,还存在明显的Pomeranchuk 效应(即温度升高可以促使绝缘体态稳定);同时,通过磁光测量发现,在相变点附近,当测量温度仅为Curie-Weiss 温度的约5%时,仍不能出现长程有序态.这两方面的实验观测结果均证实该系统在v=1 时存在阻挫效应.有关转角WSe2和MoTe2/WSe2莫尔超晶格中Mott 相变的研究工作为今后在二维半导体莫尔超晶格系统中寻找可能的量子自旋液体态奠定了基础.

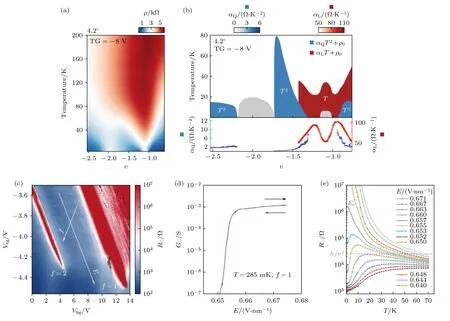
图4 TMDc 莫尔超晶格中的Mott 相变 (a) 在转角WSe2 莫尔超晶格中,样品电阻随温度和填充因子的变化[62];(b) 不同填充因子下转角WSe2 电阻随温度变化规律的概括,其中在相变临界区域电阻随温度的变化明显不同于费米液体[62];(c) AA 堆垛的WSe2/MoTe2 莫尔超晶格样品的电阻随双栅极的变化[63];(d) 保持莫尔子带半满时,外加电场使WSe2/MoTe2 中发生连续Mott 相变[63];(e) 莫尔子带半满时,不同电场下的样品电阻随温度的变化,可以清楚地看到Mott 绝缘体到金属的相变[63].Fig.4.Mott transition in TMDc moiré superlattices:(a) Measured resistance versus temperature and moiré filling factors of twisted WSe2 moiré superlattices [62];(b) summary of temperature dependent resistance of twisted WSe2 at various moiré filling factors [62];(c) resistance of AA-stacked WSe2/MoTe2 moiré superlattices versus dual gates [63];(d) Mott transition at half-filled moiré mini band induced by applied electric fields [63];(e) when the first moiré mini band is half-filled,the measured temperature dependent resistance at various electric fields,where a transition from a Mott insulator phase to a metallic phase can be clearly identified[63].

3 TMDc 莫尔超晶格中拓扑电子态的研究

第2 节所述的有关TMDc 莫尔超晶格的实验系统,从能带拓扑分类的角度来讲都是拓扑平庸的,那么是否有可能在TMDc 莫尔超晶格中实现拓扑非平庸的能带结构? 2019 年,MacDonald 课题组[79]从理论上指出,对于AA 堆垛的转角MoTe2莫尔同质结系统,在合适的参数范围内(如合适的电场、莫尔周期势的相位等),可以实现拓扑的能带结构.其后,又有更多的理论计算工作表明,在转角WSe2、转角MoS2等半导体TMDc 莫尔同质结系统中,均可以存在拓扑的能带结构[80,81,106−108].

如2.3 节所述,对于带阶相差较大的TMDc莫尔异质结系统(如WSe2/WS2),电子或空穴的波函数主要集中在其中一层,另一层的作用可以看作是提供莫尔周期势,此时系统的物理基本可以由三角格点上的单带Hubbard 模型描述[76].而对于莫尔同质结,在没有外加电场的情况下,两层TMDc是能量简并的,因此有可能存在两个能量相同的高对称性堆垛点(如图2(a)中所示的BS/Mo和BMo/S),此时的莫尔超晶格可以等效为一套六角晶格,其中两层TMDc 之间的电子跳跃就对应于六角晶格中的最近邻跳跃项,而层内的电子跳跃就对应于六角晶格中次近邻的跳跃项(图5(c)),整个系统的哈密顿量与Kane-Mele 模型[109]具有等价的形式,因此可以实现拓扑的能带结构(图5(a))[79].当第一莫尔子带被填满时,系统仍保持时间反演对称性,故K和K'谷第一莫尔子带的陈数相反,总的陈数为零,此时系统表现为量子自旋(谷)霍尔态;而当第一莫尔子带半满时,在强电子-电子相互作用情况下时间反演对称性有可能自发破缺,从而使得系统占据能带的净陈数不为零,表现为量子反常霍尔态.另一方面,外加电场可以破坏两层TMDc 的能量简并,从而驱使系统能带转变为拓扑平庸的.值得指出的是,与基于磁性三维拓扑绝缘体薄膜的量子反常霍尔效应不同[110−112],在莫尔超晶格系统中,磁性的产生并不依赖于磁性原子,而是来源于“平带”中的电子-电子相互作用导致的自发的谷极化或自旋极化,这使得在莫尔超晶格系统中量子反常霍尔效应的能量尺度原则上由莫尔子带半填充时的电子-电子相互作用强度决定.

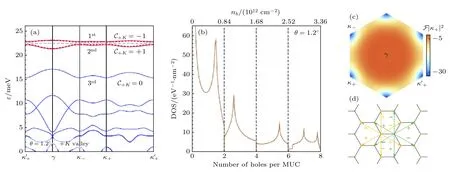
图5 TMDc 莫尔同质结中的拓扑能带结构[79] (a) 以1.2°转角的MoTe2 莫尔超晶格为例,计算得到的价带K 谷的能带结构及莫尔子带的陈数;(b)态密度随莫尔子带填充因子的变化;(c)第一莫尔子带Berry 曲率的分布;(d) 该系统中电子跳跃项的示意图,不同颜色用以区分两层MoTe2Fig.5.Topological band structures in TMDc homo-bilayer moiré superlattices[79]:(a) Calculated band structure and Chern numbers at K valley of a 1.2° twisted MoTe2 twisted moiré superlattice;(b) density of state versus moiré filling factors;(c) Berry curvature distributions of the first moiré mini band;(d) illustration of the hopping terms..

与理论预言有所不同的是,最近Shan 和Mak课题组[65]在AB 堆垛的MoTe2/WSe2莫尔异质结的价带中颇为意外地观测到了量子反常霍尔效应和可能的量子自旋霍尔效应,部分实验数据如图6所示.如前所述,理论上在莫尔同质结中实现拓扑能带的关键是存在两层简并的能带从而使系统莫尔超晶格的结构等效为六角晶格,而MoTe2/WSe2的价带带阶相差仅约200 meV[100],通过外加电场也可以减小带阶以达到使两层能带趋近简并的目的,此时电场的作用等效为调节系统层间跳跃项的强度,即空穴波函数在两层中的权重,由此可以实现莫尔子带间的能带反转和拓扑相变.实验上,在v=1 时观察到了由电场诱导的Mott 绝缘体到量子反常霍尔效应的相变,在量子反常霍尔效应区域观察到了清晰的量子化霍尔电导(图6(e)),其实现量子化的最高温度约为 2 K,这在已经发现的量子反常霍尔效应体系[15,25,110−112]中属于量子化温度较高的情况.值得一提的是,与常规拓扑相变不同,Mott 绝缘体到量子反常霍尔效应的相变涉及拓扑数的改变(陈数从Mott 绝缘体的0 变为量子反常霍尔态的–1),但实验上并未观察到能隙关闭的过程,可能的原因是相变前后自旋序的对称性发生了突变,理论上此类拓扑相变是一阶相变而非连续相变[81,113−115].当v=2 时,实验上观察到体态能隙先关闭再打开的过程,通过测量磁阻输运,发现其仅在能隙再打开之后出现了明显的平行磁场磁阻,这与(面外)自旋守恒的量子自旋霍尔效应的预期磁阻行为相符合,即在v=2 时,很可能发生了电场诱导的由能带绝缘体到量子自旋霍尔态的相变.随后的理论计算工作[116−121]也证实了AB 堆垛的MoTe2/WSe2可以出现电场诱导的拓扑相变,系统的哈密顿量接近于Kane-Mele-Hubbard 模型,并可能拥有更为丰富的相图.有意思的是,从能带排列的角度,AA 堆垛的MoTe2/WSe2和AB 堆垛的MoTe2/WSe2基本相同,但两者的能带拓扑性质却截然不同,这可能与层间耦合的强度、能带的自旋结构、莫尔周期势相位等具体参数有关.

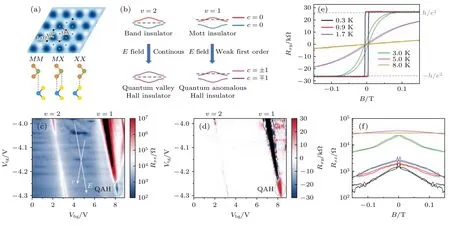
图6 AB 堆垛的WSe2/MoTe2 莫尔超晶格中的拓扑量子态[65] (a) 莫尔超晶格及高对称点堆垛方式示意图,其中M 代表Mo 或W 原子,X 代表Se 或Te 原子;(b)当莫尔子带填满时,电场诱导系统发生能带绝缘体到量子自旋霍尔效应的相变;当莫尔子带半满时,电场诱导系统发生Mott 绝缘体到量子反常霍尔效应的相变;输运测量得到的纵向电阻Rxx (c)和霍尔电阻Rxy (d)随顶栅和底栅栅压变化的二维图,测量温度为300 mK,其中绿色虚线圆圈示意的是量子反常霍尔效应出现的区域;在出现量子反常霍尔效应区域,不同温度下测量得到的Rxx (e)和Rxy (f)随磁场的变化Fig.6.Topological states in AB-stacked WSe2/MoTe2 moiré superlattices [65]:(a) Schematic plots of moiré superlattices and high symmetry stacking points,where M denotes Mo or W atoms;X denotes Se or Te atoms.(b) Schematic illustrations of electric field induced topological phase transitions.A band insulator to a quantum spin Hall insulator transition is possible when the first moiré mini band is full-filled,and a Mott insulator to a quantum anomalous Hall insulator transition could occur when the first moiré mini band is half-filled.The measured Rxx (c) and Rxy (d) versus top and bottom gate voltages at 300 mK,where the green dashed line circle denotes the quantum anomalous Hall region.At the quantum anomalous Hall region,the measured Rxx and Rxy versus Bfield at various temperatures are shown in (e) and (f),respectively.

4 总结与展望

在过去三年多的时间里,有关二维半导体莫尔超晶格的实验和理论研究工作进展迅速,揭示了一系列引人瞩目的关联电子态和拓扑电子态.从实验角度出发,二维半导体TMDc 莫尔超晶格系统至少有以下3 个特点:1)实现“平带”及电子关联效应不需要特定魔角,器件制作成功率较高;2)系统关联效应强弱及能带拓扑性质高度可调;3)除电学输运、扫描隧道谱等测量手段外,得益于TMDc优异的光学性质,基于光谱学开展的各种测量手段(磁光、荧光、激子探测等)具有很高的灵敏度,加深了人们对该系统中新奇量子物态的理解.

今后基于该系统还有可能有更加有趣的物理现象等待研究者们去发掘,比如,是否能在二维半导体莫尔超晶格体系中观察到非常规的超导电性?是否能实现分数化的量子反常霍尔效应或者分数陈绝缘体[81,122]? 是否能够为量子自旋液体态提供直接的实验证据? 另一方面,从量子物态的调控角度,二维半导体莫尔超晶格也具有独特的优势.举例来说,在二维半导体莫尔超晶格中,量子反常霍尔效应的能隙大小很大程度上取决于莫尔子带反转(即拓扑相变)时系统在莫尔子带半填充时电子-电子库仑相互作用的强度;而在二维半导体莫尔超晶格系统中,实验上观测到的Mott 绝缘体的能隙(主要由莫尔子带半填充时库仑相互作用强度决定)最大可达55 meV[52],因此如果能够调控二维半导体莫尔超晶格系统中能带发生拓扑相变时的相互作用强度,则有望大幅提高其中量子反常霍尔效应的实现温度,从而为拓扑量子计算等拓扑量子态的应用奠定基础.