FeSe/SrTiO3 高温超导体中的电子条纹相*

袁永浩 薛其坤3)4)† 李渭‡

1) (清华大学低维量子物理国家重点实验室,北京 100084)

2) (清华大学量子信息前沿科学中心,北京 100084)

3) (北京量子信息科学研究院,北京 100193)

4) (南方科技大学,深圳 518055)

单层FeSe/SrTiO3 中的界面超导增强是近年来高温超导领域的重要发现.该体系中SrTiO3 衬底对FeSe的超导增强机制已被广泛研究,其调控作用主要表现为两个方面:电荷掺杂和界面电声耦合.然而,关于FeSe薄膜本身的电子特性研究还不够充分.本文介绍该体系超导增强机制的新进展:FeSe 薄膜中的电子条纹相及其与超导的关联.通过扫描隧道显微镜结合分子束外延生长技术,对不同厚度的FeSe 薄膜进行了系统研究.我们发现FeSe 薄膜中电子倾向于排成条纹状结构,并观测到该条纹相随层厚变化显现出从短程到长程的演化.条纹相是一种电子液晶态,它源于薄层FeSe 中被增强的电子关联作用.表面电子掺杂一方面会减弱FeSe薄膜中的电子关联作用,逐渐抑制条纹相;另一方面会诱导超导相变,而剩余的条纹相涨落会对超导电性带来额外增强.我们的结果加深了对低维界面超导体系的认识,也揭示了FeSe 薄膜本征的特异性,完善了对FeSe/SrTiO3 超导增强机制的理解.

1 引言

自2006 年Hosono 课题组[1]发现LaOFeP 这一新型的超导体以来,铁基超导就成为了继铜氧化物超导体后第二类被广泛深入研究的高温超导体系.铁基超导体不仅与铜氧化物超导体有着类似的相图,而且同属于非常规超导体,针对其中超导机制的研究有助于加深对于非常规超导的理解,并对新型超导体的探索有重要意义.2012 年,薛其坤研究团队利用分子束外延手段,在SrTiO3(STO)衬底上成功制备出单层的FeSe 薄膜[2],并在其中观察到超导的显著增强现象,扫描隧道谱所得到的超导能隙为20.1 meV,远高于单晶FeSe 的 2.2 meV[3−5].抗磁性测量显示这一体系的超导转变温度在45—85 K[6−8],角分辨光电子能谱(angle resolved photoemission spectroscopy,ARPES)结果显示超导能隙闭合温度在65 K 以上[9−12],这一数值不仅是单晶FeSe 超导转变温度(8.5 K)的7.6 倍[3],而且超出所有已知铁基超导体的转变温度,也正因此,FeSe/STO 体系的研究在高温超导领域引起了广泛关注.

目前的研究表明FeSe/STO 与单晶FeSe 分属不同的超导相[13−15],SrTiO3衬底对FeSe 超导增强起了重要的作用,其贡献主要体现在两方面:一方面是衬底对薄膜的电子掺杂效应.扫描隧道谱、角分辨光电子能谱等实验结果均显示,单层FeSe的低能电子结构相较于单晶有显著的变化[2,9−12,16,17],通常在Γ点附近贡献费米面的空穴能带[18−22]移至费米能级(Fermi level,EF)以下,仅有M点附近的电子型能带贡献费米面,这不仅表明单层FeSe的费米能级存在上移,更挑战了铁基超导体中的带间散射的超导配对机制[23−27].紫外光电子能谱(ultraviolet photoelectron spectroscopy,UPS)及电子能量损失谱(electron energy loss spectroscopy,EELS)实验结果显示,在靠近界面处的STO为上层的薄膜提供了电荷转移,其本质原因是二者功函数的差别[28,29].另一方面则是STO 衬底提供的界面电声耦合效应.高分辨电子损失谱实验在FeSe/STO 样品中探测到了能量分别为92 meV 和59 meV 的F-K声子[30,31].角分辨光电子能谱实验结果则观测到单层FeSe 薄膜存在复制带[12,32,33],且复制带与主能带的能量差正好是F-K声子对应的能量,这说明衬底的声子与FeSe 的电子在界面处产生了很强的耦合,进一步的同位素效应实验更加证明了界面电声耦合对超导的影响[34].继发现衬底对FeSe 超导性质的重要影响后,更多不同的氧化物衬底被尝试用于FeSe 的生长,以试图实现更高转变温度的超导[35−39].

虽然衬底对FeSe 超导增强的贡献已经得到较为普遍的认同,但仍有一个重要的问题需要解决—STO 是薄膜生长中广泛使用的衬底材料,为什么仅有FeSe 生长在其表面时表现出了如此大幅度的超导增强? 值得一提的是,STO 衬底的晶格常数比FeSe 大(二者分别为3.905 Å与3.767 Å),通常受到如此强张应力的薄膜会完全失去超导性质,但是单层FeSe 反而表现出了显著的超导增强,因此FeSe 材料本身一定具有某些特殊的性质,使其在衬底提供的多种调控的共同作用下,超导增强效应占主导地位.

为回答这一问题,通常需要在母体中寻找材料本征的性质,根据铜氧化物以及其他铁基超导体的研究经验,母体的长程有序态往往对超导有重要影响.FeSe/STO 母体的性质却难以进行实验观测,常规调控手段无法去除STO 给单层FeSe 提供的电子掺杂,母体单层FeSe 是否存在长程有序态是未知的.近期,我们在母体FeSe 薄膜的对称性破缺研究中取得进展,分别在多层及双层FeSe/STO体系中发现了短程及长程的电子条纹相[40,41],该发现解答了FeSe 特殊性的问题,同时也对超导增强机制有了新的理解.

利用分子束外延生长(molecular beam epitaxy,MBE)以及扫描隧道显微镜(scanning tunneling microscope,STM)相结合的实验手段,对STO 衬底上生长的不同层厚FeSe 薄膜进行系统表征,这两项技术的结合不仅可以在实验上获得高质量的薄膜样品,同时也可以对不同层厚薄膜样品的局域电子结构进行表征,是观测材料体系在二维极限下产生有序电子态的理想实验手段[42].研究结果显示,STO 衬底上生长的FeSe 薄膜中电子的关联性得到了增强,这使得多层FeSe 薄膜的电子向列相的转变温度得以提高,并在缺陷附近呈现短程的条纹态[40].样品层越薄,衬底提供的张应力使关联性越强,以至于双层FeSe 中,长程的条纹相得以建立[41].可推断单层FeSe 的基态也应具有相同的长程有序态.更重要的是,具有条纹相的双层FeSe 在经电子掺杂后会产生比厚层薄膜更强的超导相,这揭示了条纹态涨落对超导额外的贡献[41].这些发现不仅揭示了FeSe/STO 薄膜在基态下新型的对称性破缺,而且完善了单层FeSe/ STO 中超导增强的特殊机制.

2 FeSe 薄膜的短程条纹相

2.1 FeSe 单晶的向列相

Kivelson 等[43]于1998 年首先提出电子液晶相的概念,电子液晶相是材料体系中介于强关联绝缘体与弱关联费米液体之间的一种特殊物质态,它通常是由电子间的关联作用所引起[43,44].因关联性大小的不同,表现为电子态不同程度的对称性破缺:打破了旋转对称性的通常被称为向列相(nematic phase);在更强关联作用下,进一步沿单轴方向打破平移对称性的通常被称为条纹相 (smectic phase 或stripe phase);最近,体现出手性的胆甾相(cholesteric nematic phase)也被实验所观测到[45,46].由于这一特殊的电子态存在于铜氧化物超导体[47−58]、铁基超导体[18−22]、拓扑材料[59−62]以及转角石墨烯[63−65]等蕴含丰富新奇量子现象的材料体系中,电子液晶相引起了广泛的研究.

铁基超导体是典型的向列相体系,多数铁基超导体在母体或欠掺杂状态下会在X 射线衍射(X-ray diffraction,XRD)[66,67]、中子散射[68−71]、扫描隧道显微镜[5,72−75]、输运[76−80]、ARPES[18−22,81]以及核磁共振[82−85]等测量中表现出旋转对称性的破缺,具体来讲即材料体系的晶格、电子轨道、电子自旋这3 个自由度沿晶体a,b两方向不等价.对铁基超导体进行掺杂后,向列性会被抑制,超导相逐步形成.在早期针对向列性的研究中,晶格、电子轨道、电子自旋这3 个自由度的相变几乎同时发生,因此也导致了向列性起源的争论,目前已确定铁基超导体向列性是由电子自由度所引发的(轨道或自旋)[79,80,85,86].轨道和自旋涨落很可能是铁基超导体中电子配对作用的来源,而二者所产生的超导可能具有不同的配对对称性,因此针对铁基超导体电子向列性起源的研究很可能对理解其超导配对有至关重要的作用[86].然而在自旋-轨道耦合的作用下,二者在铁基超导体中常常相伴而生,很难将它们进行独立研究.除此之外,有实验观测表示向列相会随着掺杂在零温条件下发生量子相变,而超导最佳掺杂浓度恰好对应该相变点,因此相变点附近非常强的量子涨落很可能是超导达到极值的关键[86−88].

FeSe 是铁基超导体中非常特殊的个例,它无需掺杂即可表现出8.5 K 的超导,并且常压下只表现出轨道的各向异性,而没有长程的磁有序态,因此在早期的研究中,这一材料被认为是能够分离轨道和自旋这两个自由度的理想体系.然而高压实验的结果显示,FeSe 的晶格在压缩的条件下,轨道的向列性会被逐渐抑制,并产生各向异性的自旋密度波态(spin density wave,SDW),这表明电子的自旋自由度可以产生对称性破缺[89−94].进一步的理论结果表明,FeSe 在常压下不表现长程磁有序的原因来自于磁阻错现象,有多种能量相近且打破旋转对称性的磁涨落相互竞争,以至于阻碍了长程磁序的产生,而在高压环境中,这种竞争的平衡被打破,使得自旋的向列性得以复现[95−98].

2.2 STO 上多层FeSe 薄膜的短程条纹相与向列性增强

STO 上生长的FeSe 薄膜受到了衬底张应力的作用,晶格常数大于单晶本身,因此可视作施加负高压.实验表明,FeSe 薄膜向列相的转变温度相比单晶有显著的提高[99],并且越薄层FeSe 的向列性会进一步增强,这说明晶格增大导致了电子关联性的增强.根据理论,当电子关联性足够强时,体系有可能产生进一步的对称性破缺,即诱发条纹态[43,100].2017 年我们对30 层FeSe 薄膜的研究工作证实了这一对称破缺的存在[40].

图1(a)所示为FeSe 晶格结构示意图.图1(b)是在STO 上生长的30 层FeSe 薄膜典型的STM形貌图,从图1(b)可见薄膜呈现出类似“迷宫”图案的向列畴界,畴界两侧即为孪生向列畴.通常来说FeSe 薄膜存在Fe 空位缺陷,它们会使得最表面的相邻的Se 原子呈现出“哑铃”状的缺陷形貌(如图1(c)所示,晶格结构如图1(a)所示).在表面物理研究中,缺陷往往可以当作窥探材料体系本征行为的窗口,当缺陷与周围电子产生相互作用时,即可使电子结构在实空间的局域态密度上得以呈现.通过对缺陷的观测,发现了FeSe 新的局域对称破缺—短程条纹相(见图1(c)和图1(d)中箭头所指位置).从对称性的角度,这些短程的条纹态不仅证明了FeSe 确实打破了C4 旋转对称性(向列性),而且也局域地打破了单方向的平移对称性,预示该体系中存在更强的相互作用.条纹态在单个畴中的取向是相同的,而在相邻畴间是相互垂直的(图1(c)中的黄色虚线标注了畴界所在位置).原子分辨图的结果显示,条纹态沿Se-Se 格子的对角方向排布,即Fe-Fe 格子方向,且周期为非公度的1.9 nm.

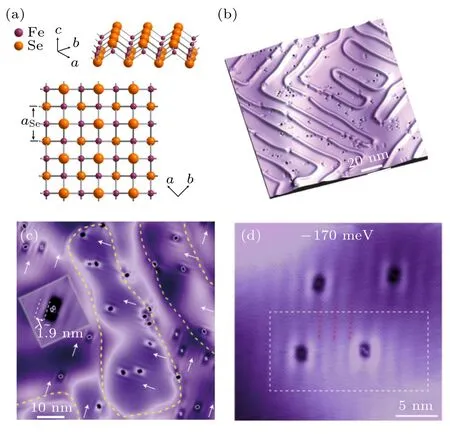
图1 FeSe 的晶格结构及形貌表征[40] (a) FeSe 晶格结构示意图;(b) 30 层FeSe 薄膜的STM 形貌图,图中迷宫状纹路即向列畴界;(c) FeSe 薄膜畴界附近的形貌图;(d) 缺陷附近短程条纹态的形貌图Fig.1.Lattice structure of FeSe and its topographic images[40]:(a) Lattice structure of FeSe;(b) STM topographic image of FeSe thin film,the maze-like patterns are the nematic domain walls;(c) topographic image near nematic domain wall;(d) short-range stripes near defects.

事实上,这样的条纹结构可对应两种可能的物理图像:一是由缺陷散射引起的准粒子干涉;二是真正的条纹状的电荷有序态.准粒子干涉与能带结构紧密联系,因此能带的色散会使准粒子干涉信号存在相应的色散;相反,稳定的电荷序在各个能量下的大小是相同的,不会随能量而产生色散.由于STM形貌图反映的是态密度对能量积分后的信号,准粒子干涉信号通常会由于积分效应而被减弱或消除,因此形貌图中观测到的大概率是条纹态电荷序.

图2 中的微分电导图像(dI/dVmap)进一步证明了条纹相的电荷序本质.微分电导图像可以呈现出不同能量下态密度在实空间的分布,不存在形貌图中的积分效应,因此可准确区分准粒子干涉与电荷序.图2(b)—(p)中的实验结果显示,缺陷附近条纹态的周期在相当大的能量区间内都不发生改变(图中白色箭头所示),这说明它是电荷序而不是准粒子干涉.不仅如此,准粒子干涉信号也同时被观测到(图中黄色虚线所示),准粒子干涉信号呈现出空穴型的色散关系,对应布里渊区M点附近的带间散射过程.从图中条纹态与准粒子干涉信号可以确定出不等价的a,b格子的方向,同时也可以明确二者的波矢在倒空间均沿Г-Mx方向[40].

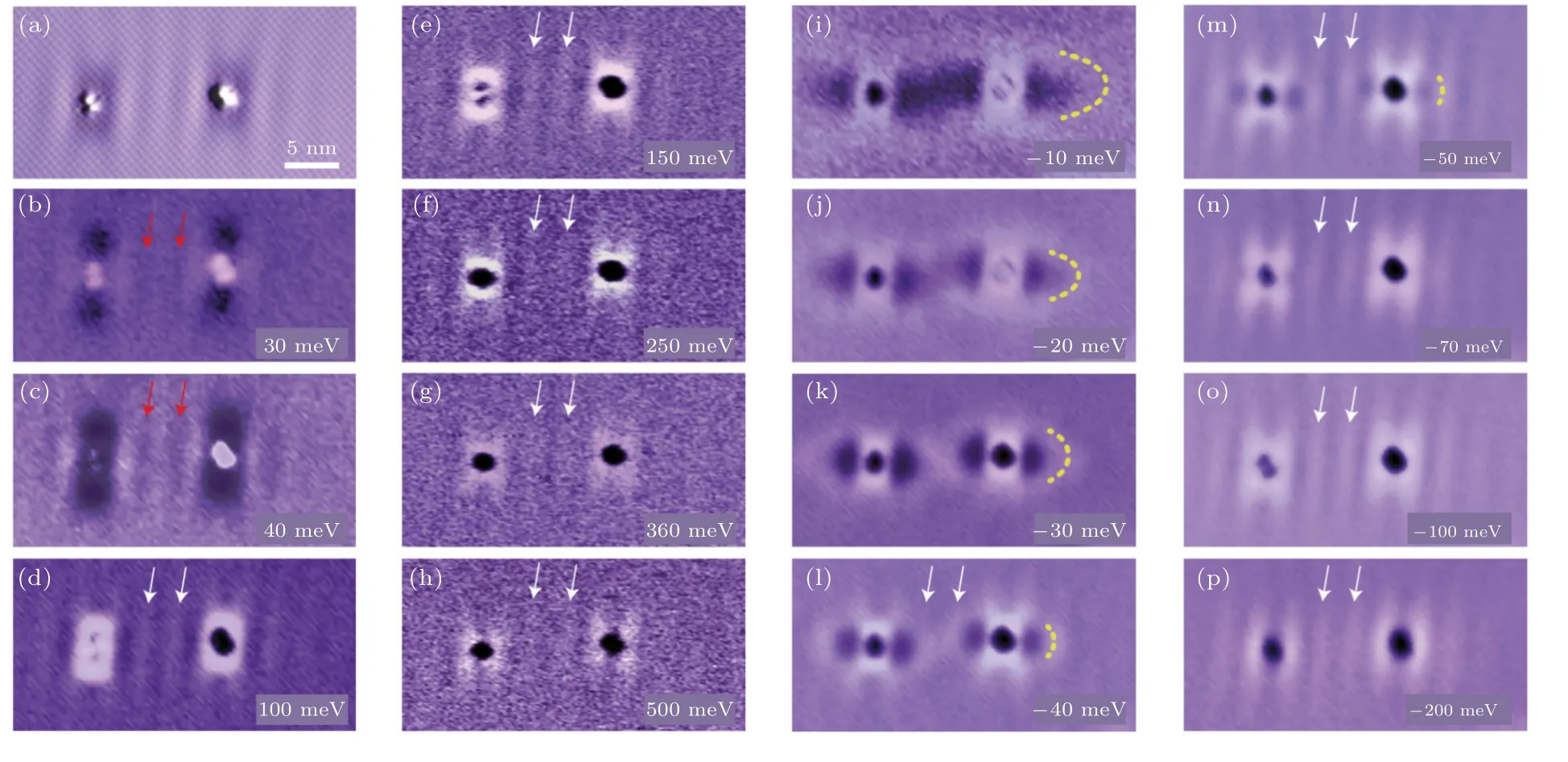
图2 条纹态与准粒子干涉[40] (a) 两个缺陷附近的形貌图;(b)—(p)不同能量下的微分电导图像,从中可以观察到不随偏压改变的条纹态以及随偏压变化的准粒子干涉Fig.2.Stripes and quasiparticle interference[40]:(a) STM topographic image of two impurities;(b)–(p) dI/dV maps under different energies,in which energy independent stripes and energy dependent quasiparticle interference patterns are observed.

短程条纹态在体系原本旋转对称性破缺的基础之上进一步打破了缺陷附近单方向的平移对称性,这种对称性破缺与长程有序的条纹相行为相对应,虽然短程条纹相缺少长程相干性,但这说明FeSe 薄膜内有了形成全新的长程序的趋势,STO衬底张应力的作用促进了这种长程序的建立.由此可见FeSe 薄膜的向列性增强与短程条纹态的出现均是由电子关联性调控的,关联性的增强将FeSe推至非常接近长程条纹相的相变点,使得向列性的背景下有着很强的条纹电荷序涨落,而铁空位缺陷打破了晶格的对称性,促使电荷序涨落以短程条纹态的形式钉扎在缺陷附近.

条纹相与向列相的关系在变温实验中得以验证[40].如图3(a)所示,当样品处于77 K 的环境中时,畴界仍旧是存在的,这说明此时的FeSe 薄膜仍处于二重旋转对称性的向列相.当温度进一步上升时(如图3(a)—(h)),畴界逐渐变弱,直至120 K时完全消失,因此可以推断30 层FeSe 薄膜的向列相转变温度为120 K,相较于单晶FeSe 的90 K 有显著提升,这一结果也与ARPES 对向列性增强的观测一致[99].然而缺陷附近的条纹相在77 K 已完全消失(如图3(e)),只有当温度降到60 K 以下时,条纹态才会复现(图3(f)—(h)),这说明条纹相是在旋转对称性破缺的基础之上才可以产生的.不仅如此,条纹相的周期并不会因温度变化而改变(如图中白色箭头及红色虚线区域所示).

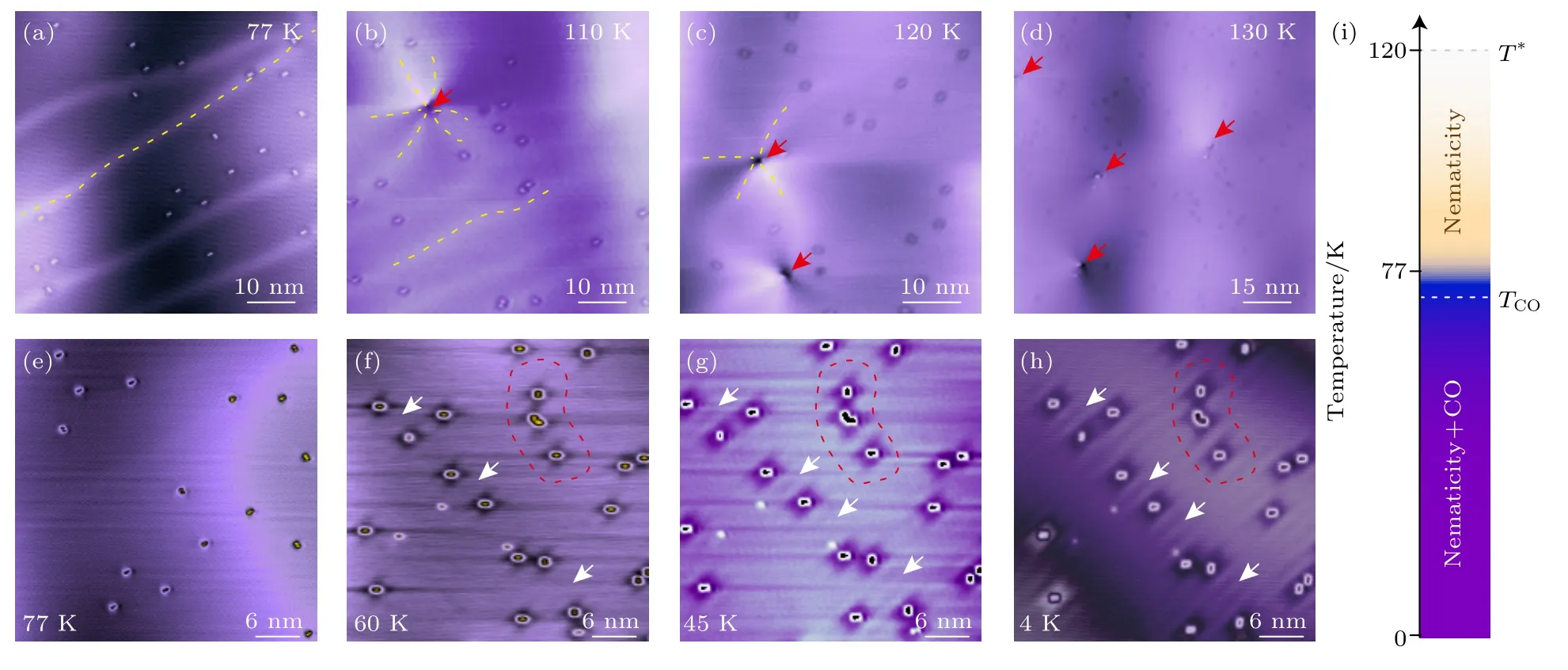
图3 向列性与短程条纹态随温度的演化[40] (a)—(d) 向列畴界随温度的演化;(e)—(h) 短程条纹相随温度的演化;(i)向列相与短程条纹相的相图Fig.3.Temperature evolution of nematicity and short-range stripe phase[40]:(a)–(d) Temperature evolution of nematic domain walls;(e)–(h) temperature evolution of short-range stripes;(i) phase diagram of nematic phase and short-range stripe phase.

图4 展现了缺陷与这种短程条纹相之间的相互作用,当样品存在条纹态时,哑铃状的缺陷态会与最表面Se 原子晶格产生大于10°的转角(图4(a)和图4(b)),而在77 K 条纹态消失时,哑铃状的缺陷是完全沿着Se 原子晶格的(图4(c)).这说明缺陷与条纹态确实存在相互作用,条纹态的产生与缺陷的钉扎作用是紧密关联的[40].

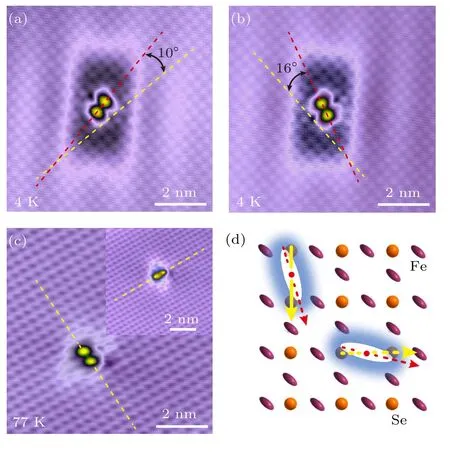
图4 缺陷与短程条纹相之间的相互作用[40] (a),(b) 短程条纹相存在时,缺陷态存在大于10º转角;(c) 77 K 的缺陷态,此时由于没有短程条纹相,缺陷态也没有转角;(d) 缺陷态转角的示意图Fig.4.Interaction between defects and short-range stripes[40]:(a),(b) The off-axis impurity state with the appearance of short-range stripes;(c) impurity state at 77 K,the off-axis effect is absent due to the lack of short-range stripes;(d) schematic of the off-axis impurities.

接下来讨论电荷序与超导的潜在关系.向列性是铁基超导体具有的本征性质,在衬底调控的作用下,FeSe 薄膜内部的向列性得到了增强,并且诱导了短程的条纹态,通常来讲类似对称性破缺的建立会很大程度上抑制超导的产生,这可以解释多层FeSe 薄膜中不存在类似单晶样品的超导现象.值得一提的是,层数越薄的FeSe 受到了越强的衬底张应力作用[11],理应拥有更强的电子液晶相,这意味着超导会被进一步抑制.然而在单层极限下,衬底给予薄膜的电荷转移会减弱电子间的关联作用,使单层FeSe 产生了高温超导现象.由此可见,薄层FeSe 中的电子关联性、电荷序以及超导之间可能存在着更复杂的关系.我们以双层FeSe/STO薄膜作为出发点,对这一问题开展了研究,已取得了突破,在其中观察到了长程的条纹相,并揭示了其与超导之间的关系[41].

3 FeSe 薄膜的长程条纹相

无论是铜氧化物还是铁基超导体,对于母体性质的研究均对超导相的理解起到重要的推动作用.然而对于单层FeSe/STO 体系,其母体性质(或称之为基态)的研究却十分困难,这是因为STO 衬底会给FeSe 提供非常稳定的电子掺杂,在实验中很难调控单层FeSe 的掺杂浓度.双层FeSe 是模拟单层母体(基态)行为的理想平台,STO 衬底提供的电子掺杂在双层薄膜中几乎完全消失,其晶格常数也与单层FeSe/STO 最为接近[10,11],因此它应当表现出类似单层FeSe 母体的强关联行为(真正单层FeSe 母体应有更强的关联性).实验结果显示,在电子强关联作用下,双层FeSe/STO 薄膜产生了长程的非公度条纹相,这一全新的长程序与超导增强有着密切的联系[41].

图5(a)是在双层FeSe 薄膜上采的微分电导图.从图5(a)可以看出非常明显的长程条纹态,与30 层FeSe 薄膜中的短程条纹相相比,此处的条纹态并不依赖于缺陷而存在,并且打破了全空间的旋转对称性以及单方向的平移对称性,这说明双层FeSe 薄膜中建立了真正的长程条纹相.从图5(a)还可以清晰地观察到条纹相的畴界(图中微分电导较高的亮线),畴界两侧的条纹态相互垂直.图5(a)和图5(b)中白色虚线所示的电子态变化并不来自于双层FeSe,而是下方单层薄膜中2×1 重构畴界映衬出的电子态起伏,从图中可见条纹态可以连续穿越虚线区域,因此二者没有直接关联.

此处长程条纹态的周期约为2.0 nm,对应到空间的波矢为q0=0.19qSe(其中qSe为Se-Se 格子的布拉格点),其方向沿Fe-Fe 格子方向.以上结果与30 层FeSe 中缺陷附近的条纹态相符,这说明二者的起源相同,厚层样品中的短程条纹态是此处长程条纹态的“前驱体”[41].

长程条纹态同样不随能量演化.图5(c)中主图呈现了三阶电导(d3I/dV3)随空间及能量的变化,该数据采集自图5(a)中的红色虚线箭头位置.图中可见条纹态主要在–100 meV 至–30 meV,30 meV 至60 meV 以及90 meV 至100 meV 的能量范围内最为显著,这3 个能量区间的d3I/dV3 的平均值如图5(c)中右图所示,而其周期如图5(c)中下图所示,可以清晰地看出条纹态的周期不随能量改变,仅有相位会在30—60 meV 能量区间产生反相,这证明双层FeSe 中的长程条纹态的确是电荷有序态.在铁基超导体中,类似的长程条纹相仅在施加了单轴应力的LiFeAs 单晶中被观测到[75],而此处FeSe 薄膜的长程条纹相是在衬底提供的双轴应力下实现的.

图5 双层FeSe 的长程条纹相[41] (a) 微分电导图像中的长程条纹相;(b) 单畴形貌图中的长程条纹态以及对应的傅里叶变换;(c) 条纹态周期对能量依赖的分析结果Fig.5.Long-range stripe phase in 2 unit-cell (UC) FeSe[41]:(a) Long-range stripe phase in a dI/dV map;(b) topographic image of long-range stripes in a single domain and the corresponding Fourier transformation result;(c) energy dependence analysis to the periodicity of stripes.

层厚依赖的实验结果显示,长程的条纹相仅存在于双层FeSe 之中.图6(b)—(d)是在单层及二层FeSe 薄膜的台阶附近采集的微分电导图(其对应形貌图及微分电导谱如图6(a)所示).可以清晰看出条纹态及畴界截止于台阶边缘,它们仅存在于左侧双层薄膜中,单层FeSe 中完全没有电子液晶态.双层和三层薄膜之间呈现出不同的演化,如图6(f)—(h)所示,畴界可以穿过台阶边缘同时存在于双层及三层膜中,然而长程条纹相仅存在于左侧的双层FeSe 中,此处三层薄膜与多层薄膜均具有向列性,因此电子结构在二到三层之间实现了条纹相至向列相的转变.不仅如此,台阶两侧薄膜的条纹相与向列相畴界是共享的,印证了条纹相与向列相具有相同的起源,条纹相可以看作在向列相的基础上由电子关联性进一步增强所诱导的平移对称破缺,它们是FeSe 的本征性质在不同程度电子关联作用调控下的不同表现[41].我们在实验中对四层、五层的薄膜也进行了研究,它们的性质与三层乃至厚层FeSe 相似,因此可以排除奇偶层效应的影响.

图6 条纹相的层厚依赖[41] (a) 单层及双层FeSe 台阶附近的形貌图及它们对应的扫描隧道谱;(b)—(d) 该台阶附近不同能量的微分电导图像;(e) 二层及三层FeSe 台阶附近的形貌图及它们对应的扫描隧道谱;(f)—(h) 该台阶附近不同能量的微分电导图像Fig.6.Thickness dependence of long-range stripe phase[41]:(a) STM topographic image on a step edge between 1 UC and 2 UC FeSe and the corresponding dI/dV spectra;(b)–(d) dI/dV maps taken on this step edge with different energies;(e) STM topographic image on a step edge between 1 UC and 2 UC FeSe and the corresponding dI/dV spectra.(f)–(h) dI/dV maps taken on this step edge with different energies.

上述实验结果显示,FeSe 薄膜处于二维极限时存在着丰富的电子态.如图7 所示,双层FeSe具有独特的长程条纹相,由于其受到的关联性调控与下面的单层薄膜最为接近,这一长程序可视作单层FeSe/STO 的基态;单层FeSe 在衬底提供的电子掺杂作用下,失去了电子液晶态而表现出高温超导特性;在更厚层的三层及以上的薄膜中,条纹相转变为向列相,长程条纹态被抑制后仍存在很强的涨落,缺陷附近区域仍可复现出局域的条纹态行为.

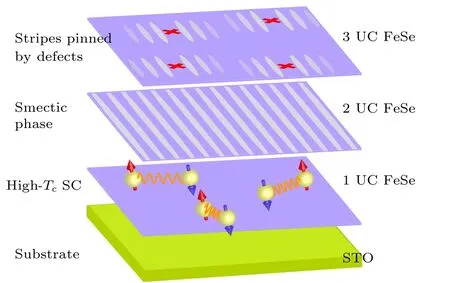
图7 不同层厚FeSe 薄膜电子结构的示意图[41]Fig.7.Electronic structures of FeSe thin films with different thickness[41].

薄层FeSe 中丰富的电子态来自于电子关联性对层厚的敏感响应,这是由STO 衬底给薄膜提供的张应力以及电子掺杂的共同调控作用引起的.先前的研究结果显示,张应力导致的晶格增大现象在50 层FeSe 中仍可观测到,然而电子掺杂只对单层FeSe 产生显著作用[11],二者在最初三层FeSe 中的微妙平衡诱导出了多种电子态.最靠近衬底的单层FeSe 受到了最强的张应力作用,本应体现出最强的条纹相,而电子掺杂抑制了其关联性,使得条纹相、向列相都不复存在,表现出了高温超导特性;在双层FeSe 中,张应力作用诱导的关联性增强依旧显著,但是电子掺杂戛然而止,这导致其表现出母体的条纹相;在三层及以上的FeSe 中,张应力作用逐步减弱,关联性已不足以维持条纹相,于是呈现出增强的向列相,向列相的转变温度随膜厚增厚逐渐降低直至收敛到体相的90 K[41].

4 FeSe 电子条纹相与超导的关联

在铜氧化物高温超导体中,母体与掺杂后的超导相存在二重关联:母体的长程反铁磁序与超导之间存在竞争关系,然而当长程序在掺杂的效应下被抑制后,剩余的反铁磁涨落很可能在库珀对的形成中贡献了电子间的相互作用.单层FeSe/STO 是否具有类似的机制是值得研究的.既然双层FeSe可近似视作单层高温超导的母体,那么随着电子掺杂应该可以观察到长程条纹态的抑制以及超导的产生,在这一过程中电子液晶相与超导的关系将得以呈现.

通过在FeSe 薄膜上进行Rb 原子表面掺杂,观察到了条纹相与超导的关联.实验结果如图8(a)—(e)所示,条纹态首先在Rb 原子聚集程度较高的区域被抑制.随着整体掺杂浓度提高,具有条纹态的面积逐步减小,条纹相的相干性逐渐被破坏,当覆盖度达到0.0265 ML (monolayer)时(每个Rb贡献一个电子,对应掺杂浓度约为0.0265 e/Fe 原子),条纹相完全消失,与此同时超导恰好产生(如图8(f)所示).上述实验现象证明电子液晶相与超导存在竞争的关系,只有当条纹相完全抑制后超导才得以建立.

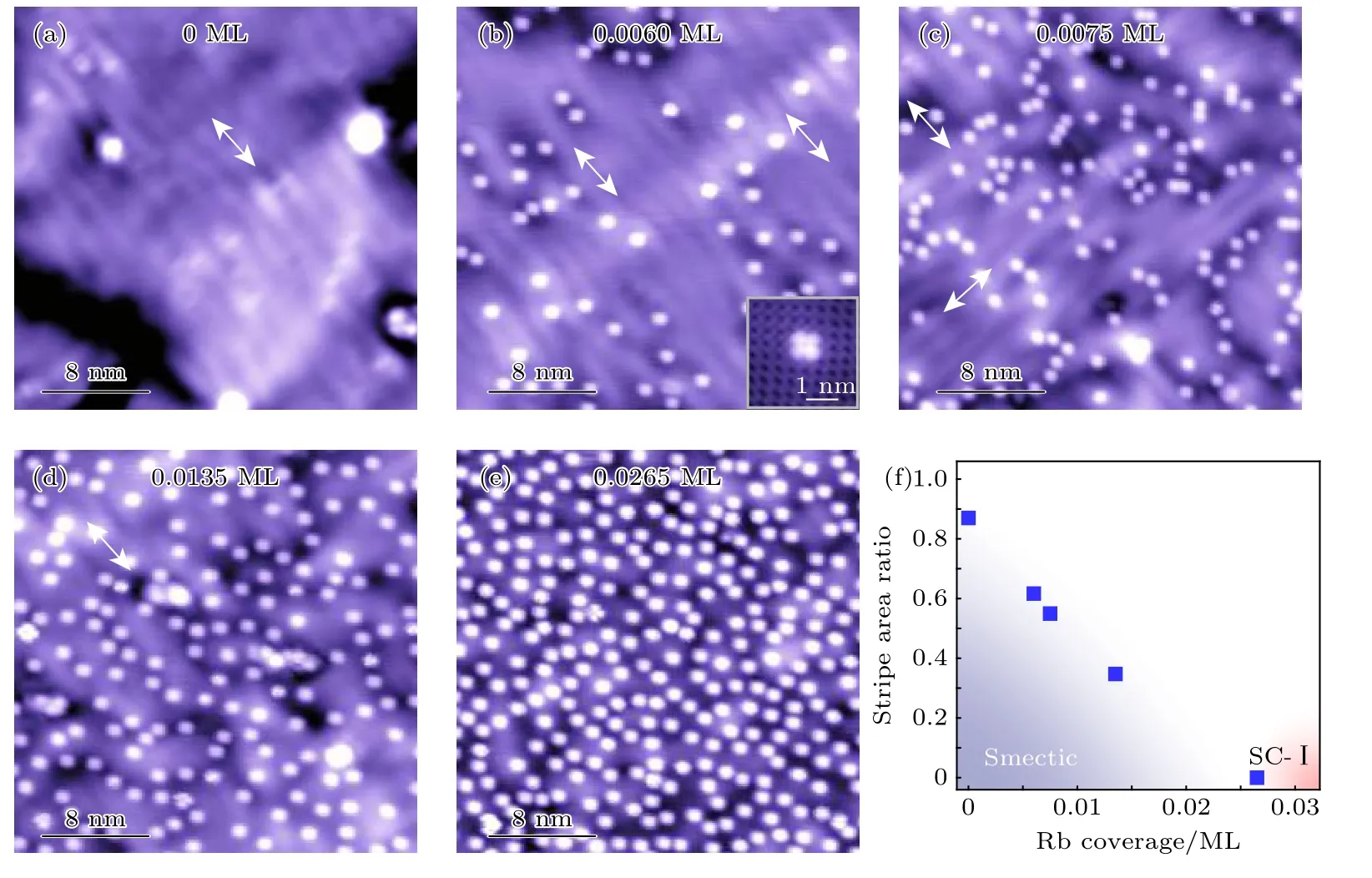
图8 表面Rb 原子掺杂对条纹相的抑制[41] (a)—(e) 不同掺杂浓度下,双层FeSe 的表面形貌图;(f) 条纹相面积占比随掺杂浓度的变化关系.Fig.8.Suppression of stripe phase by surface Rb doping[41]:(a)–(e) STM topographic images taken on 2 UC FeSe at different doping concentrations;(f) the stripe area ratio at different doping concentrations.

条纹态涨落对超导的贡献在进一步的掺杂后得以体现,图9 总结了双层及三层薄膜超导能隙随掺杂浓度的演化过程.Rb 原子的分布的不均匀性导致了超导存在涨落,因此在研究中采取了统计的方法,从超导均一性以及能隙大小两个方面表征超导的强弱,两个方面的研究结果均显示具有条纹相的双层薄膜在掺杂后拥有更强的超导性质[41].

首先在超导均一性方面,每个掺杂浓度的dI/dV谱均以超导能隙为标准分成“好超导”及“坏超导”两组,在双层及三层FeSe 上不同掺杂浓度好超导组的平均谱分别如图9(a)和图9(c)所示,而坏超导组的平均谱分别如图9(b)和图9(d)所示.在双层FeSe 中,0.027 ML 的Rb 掺杂即可诱导超导,而在三层中则需要0.038 ML.

每个掺杂浓度下的好超导占比可以反映该掺杂浓度对应的超导均一性.双层及三层FeSe 好超导占比随掺杂浓度的演化如图9(e)所示,二者的超导均一性都随掺杂表现出拱形演化,且双层薄膜的“拱顶”呈现出一个平台,好超导占比也更高,说明双层膜的超导均一性更好.此外,最佳掺杂浓度处的平均谱同样显示双层FeSe 拥有更强的相干峰(图9(f)).

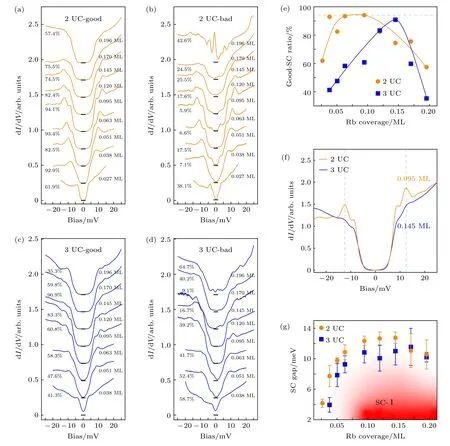
图9 双层、三层FeSe 中由表面Rb 原子掺杂引入的超导相[41] (a),(b) 双层FeSe 上不同掺杂浓度下“好超导”与“坏超导”组的平均谱;(c),(d) 三层FeSe 上不同掺杂浓度下“好超导”与“坏超导”组的平均谱;(e) 好超导比率随Rb 掺杂浓度的演化;(f) 图(a)与(c)中超导最均匀对应的掺杂浓度下的平均谱;(g) 超导能隙平均值与掺杂浓度的依赖关系Fig.9.Superconducting phase in 2 UC and 3 UC FeSe induced by Rb surface doping[41]:(a),(b) The averaged dI/dV spectra in“good superconducting”and“bad superconducting group”of 2 UC FeSe at different doping concentrations;(c),(d) the averaged dI/dV spectra in“good superconducting”and“bad superconducting group”of 3 UC FeSe at different doping concentrations;(e) the evolution of good superconducting ratio at different doping concentrations;(f) the averaged dI/dV spectra extracted from(a) and (c) at the doping concentrations with optimal homogeneity;(g) dependence of the averaged superconducting gap size on doping concentration.

另一方面,超导能隙的平均值的研究结果如图9(g)所示,双层及三层FeSe 的超导能隙同样呈现出拱形演化,且在最佳掺杂浓度处,双层膜的超导能隙比三层膜更大(双层为12.75 meV,三层为11.56 meV),因此从能隙大小的角度同样可以认为双层膜的超导更强,这一实验结果与K 原子表面掺杂的FeSe 薄膜相同[101,102].

上述实验结果充分说明双层FeSe 薄膜不仅在非掺杂的母体状态时表现出了条纹相,且在电子掺杂后拥有更强的超导态.这一现象揭示了FeSe 的电子关联性与超导的潜在关系,即长程条纹态被电子掺杂抑制后,剩余的涨落效应促进了超导增强,这与铜氧化物的相图相一致.而在更薄的单层FeSe中,更强的电子关联性理应诱导更强的条纹态涨落,所以其中条纹态涨落对超导的贡献应当比双层更加重要.

结合前人研究成果及我们的实验[10,11,40,41,103−105],FeSe 薄膜的电子结构可总结成图10 所示相图,图中总结了超导态及电子液晶态随薄膜层数及电子掺杂浓度的演化关系,其中薄膜层数实际上反映了张应力强度.由于张应力及电子掺杂间微妙的平衡作用,条纹相仅出现在双层FeSe 薄膜中,在条纹相的两侧均会产生新的相变.在三层及以上的薄膜中,张应力的减弱使得长程条纹相消失,薄膜表现出具有短程条纹态的向列相.这些电荷有序态与超导相竞争,使得双层及以上的薄膜中没有超导,唯有当薄膜厚度进一步增加使得向列性减弱到一定程度,类似于单晶样品中的超导相才会出现(图中的SC-II 相).在相图的另一侧,在没有电子掺杂的情况下,单层FeSe 本来应具有更强的电子条纹相,但是衬底提供的电子转移使得关联性被抑制,仅有很强的条纹态涨落保留其中,并贡献了额外的超导增强.因此,FeSe/STO 体系中的条纹态涨落是除了电子掺杂、电声耦合以外的另一个增强超导的重要机制.条纹相极有可能是单层FeSe/STO 母体固有的长程序,是FeSe 相比于其他材料的特殊之处,这可以在一定程度解释为什么唯有单层FeSe/STO 实现了大幅度的超导增强.

图10 FeSe/STO 随温度、层厚、电子掺杂变化的相图[41],其中超导转变温度来自ARPES 数据[10,11,104,105]Fig.10.Phase diagram of FeSe/STO as a function of temperature,thickness and doping[41].The superconducting transition temperature is derived from ARPES data[10,11,104,105].

5 FeSe/STO 条纹相的起源

既然条纹态是张应力条件下FeSe 薄膜固有的长程序,理解它的起源是研究FeSe 内电子相互作用的关键,不同相互作用机制甚至可诱导出不同的超导配对对称性[86,106−110].一般地,材料体系内的巡游电子和局域电子均可以引起电子液晶态的相变,二者的实验表现有所不同,下面分别作讨论.

1) 巡游电子引发条纹相的机制基于费米面嵌套,这通常需要在EF附近存在两段相互平行的等能面,电子在平行能带间的散射会占据主导作用,进而诱发费米面失稳,而电子在倒易空间的散射波矢即对应条纹态在实空间的周期.

图11 展示了条纹相的波矢与不同层厚FeSe薄膜的能带的直接比较[41].旋转对称性的破缺导致了Γ-Mx与Γ-My方向能带不等价,由准粒子干涉与条纹态之间的关系可知条纹态的波矢沿Γ-Mx方向,又由条纹周期可知波矢大小为q0=0.309 Å–1(如图11(a)所示).图11(b)—(f)呈现了Γ-Mx方向能带随FeSe 薄膜层厚的演化,图中能带取自ARPES 实验数据,FeSe 在EF附近的确存在两支互相平行的能带(图中绿线标记的dyz及蓝线标记的dxy能带),理论上二者的带间散射有可能使FeSe产生不随能量改变的条纹态,但经仔细比较后即可排除这一可能.首先,双层FeSe 中条纹态的波矢q0明显小于带间散射波矢qs=0.406 Å–1;其次,空穴型的dyz能带的带顶位于EF以上60 meV 处,故该能量以上不再存在这一带间散射过程,然而实验中观测到的条纹态在高能依旧可被观测到(见图6);最后,双层FeSe 中的长程条纹态与多层的短程条纹态周期是相同的,然而带间散射波矢qs随层厚的增加有缩短的趋势.因此单独使用巡游电子模型并不能很好地解释实验观测.

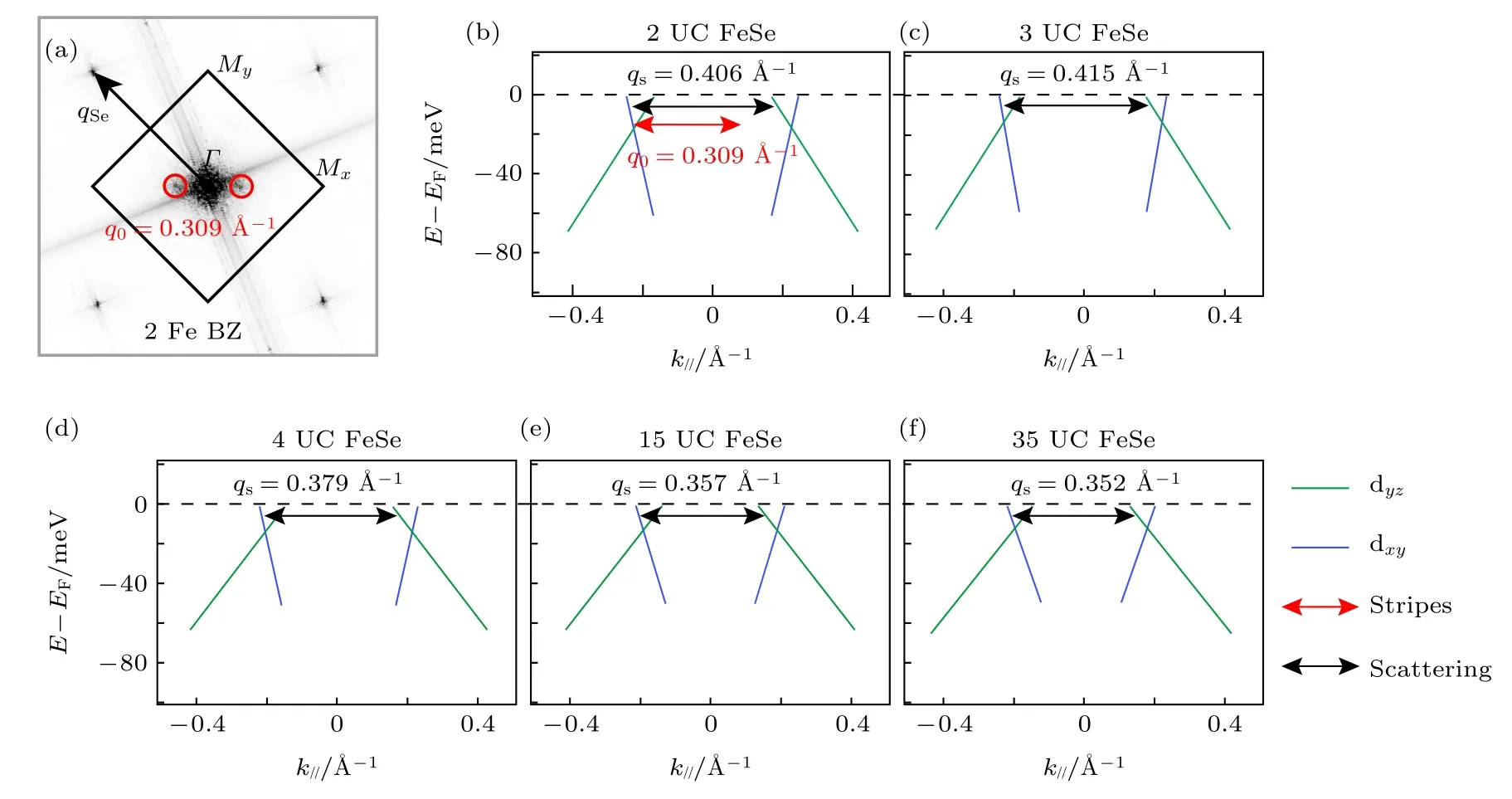
图11 条纹态与能带的比较[41] (a) 条纹态对应的傅里叶变换;(b)—(f) M 点附近能带随层厚的演化,能带结构取自ARPES 数据Fig.11.Comparison between stripes and band structure[41]:(a) The Fourier transformation result of stripes.(b)–(f) Band structures near M point with different film thickness.The band structures are extracted from ARPES data.

2) 铁基超导体的J1-J2 模型通常用来描述局域电子行为[71,95−98],基于这一模型的理论计算可以给出多种打破旋转对称性的散射波矢,其中包括q(π,0),q(π,π/5),q(π,π/3),q(π,π/2)以及其他可能的散射波矢q(π,Q<π/2).FeSe 单晶中,上述散射波矢相互竞争,从而导致了向列相与自旋密度波的分离.在FeSe 薄膜中,应力的作用很可能使其中某一特定的散射波矢增强,从而产生稳定的长程条纹态,然而基于局域电子模型给出的所有散射波矢均为公度的,与实验中观测到的非公度散射波矢不相符合,因此单独使用局域电子模型同样无法很好地解释条纹相的产生.

综上所述,单一使用巡游电子模型或局域电子模型均无法解释FeSe 薄膜中的条纹相,因此目前的理论结果无法给出条纹相的具体成因.FeSe 薄膜中的非公度条纹相极有可能来自巡游电子与局域电子的共同作用,然而这一猜想仍须进一步的理论计算的验证.

6 总结与展望

本文回顾并讨论了FeSe/STO 体系的电子液晶相、超导性质以及二者之间的关联,揭示了FeSe薄膜本身所具有的特异性及其在超导增强中的重要作用.向列相是FeSe 单晶具有的本征性质,这一性质在受到衬底的应力调控后得到增强,使得在三层及以上的FeSe 薄膜中诱导出缺陷相关的局域条纹相,而双层FeSe 薄膜可进一步表现出关联性更强的长程条纹相.电子液晶态会与超导竞争,从而抑制薄膜中的超导电性.双层FeSe 的条纹相可在电子掺杂后完全消失,进而产生出比厚层薄膜更强的超导,这说明条纹态涨落对超导具有增强作用.另一方面,单层FeSe/STO 的电子关联性理应更强,本应具有更强的条纹相,而衬底提供的电荷转移使得单层FeSe 的条纹相被抑制,表现出高温超导性.条纹态的涨落对超导增强的额外作用,是继界面电声耦合、电荷转移后,在FeSe/STO 体系发现的另一促进超导的机制.这一机制也很好地解释了为什么FeSe 是唯一在STO 衬底上实现显著超导增强的材料体系.我们对电子条纹相的研究完善了对该体系本征性质的认识,也为铁基超导体的研究提供了新的视角.

目前针对FeSe 条纹相的认识还存在局限性.首先,它的起源尚未被完全解释清楚,巡游电子与局域电子均可能对条纹态产生重要影响,但仍缺少可完全与实验现象吻合的理论模型;其次,目前对于衬底提供的张应力调控作用的认识还有待加深,可尝试在晶格常数更大的衬底上生长FeSe 薄膜,并对其中的条纹相进行更深入的研究;再次,铁基超导体中电子的轨道与自旋自由度往往是紧密关联的,此前实验已经观测到FeSe 薄膜内的反铁磁现象[111],但尚不足以说明它就是条纹型的自旋密度波.条纹相与磁性的关联将对超导研究产生更大的启发;最后,按照我们的理解,单层FeSe/STO的基态应表现出更强的条纹相,在今后的实验中可尝试抽离单层薄膜中的电子,对其基态电子结构进行深入研究.

总体而言,FeSe/STO 高温超导体系的基态(或母体)仍有广阔的研究空间,其中电荷序、磁有序等性质尚未完全澄清,它们与超导相之间的关联也有待深入挖掘.条纹相的发现推进了这一领域的认知,将FeSe 与铜氧化物高温超导的相图更好地统一起来.期待这个领域中会迸发出更多新奇有趣的物理,为寻找低维高温超导材料带来新的思路.