利用复变格林函数法的Eshelby夹杂外场的一般显式解析解

李瑞,唐智亿,苏飞,范文,马利锋

(1.西安交通大学机械结构强度与振动国家重点实验室,710049,西安;2.长安大学地质工程与测绘学院,710064,西安)

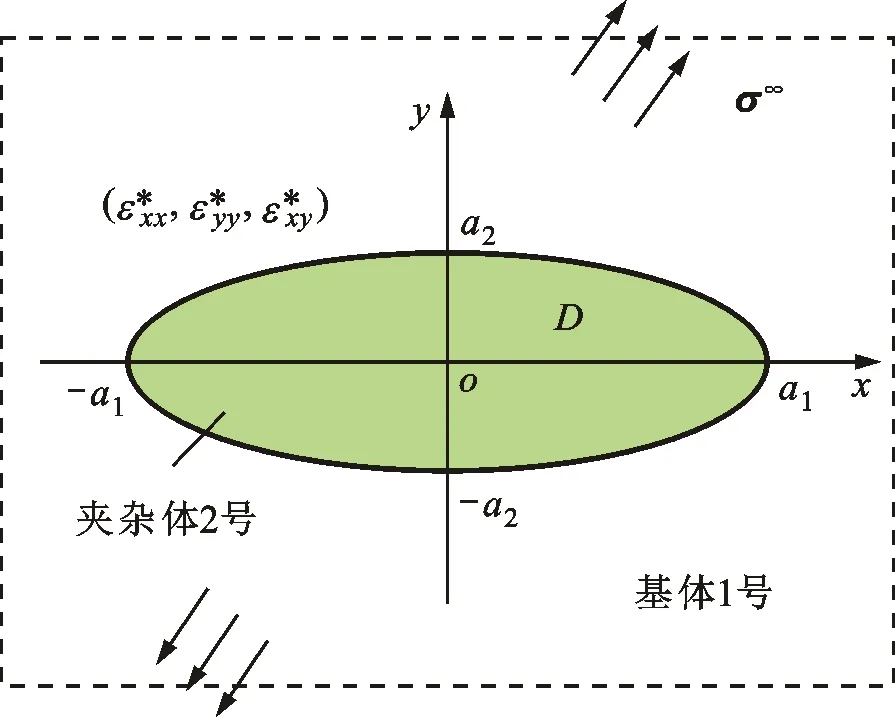
图1 椭圆异性夹杂

对于异性夹杂问题,Eshelby等[2-3]开创性地证明了当异性夹杂为椭球且夹杂内的特征应变分布均匀时,其内部应变场必均匀,这个标志性结果概括了早期关于椭圆异性夹杂的努力[10-11]。Eshelby的这一成果可用经典的四阶Eshelby张量来表述,这为系统地研究弹性固体中的夹杂问题奠定了基础[12]。该椭圆异性夹杂模型及其相关模型通常被称为Eshelby夹杂力学模型,它已成为固体力学的经典成果之一。与Eshelby夹杂的内场解相比,虽然前人对基体的弹性场也做了大量的工作,但是研究并不深入[3,13]。

实际上,外场的显式解析表达仍然是Eshelby夹杂力学中未完善解决的理论问题之一。例如,由于含有液体夹杂的弹性复杂模型可广泛用于岩石、土体中微观应力分析,因此在Eshelby夹杂力学框架下,求解液体夹杂外场成为一个主要问题[14-16]。尽管该问题已引起诸多学者的关注,但是有关外场的显式解析解的研究仍然很少。

与三维Eshelby夹杂模型相比,二维Eshelby夹杂模型简单又具有普遍性,同时仍能有效反映夹杂内外的基本变形行为。此外,二维模型便于引入更多的数学工具来分析外场,因此,本研究就着手探讨平面椭圆异性夹杂问题。

处理平面椭圆异性夹杂问题主要有两种方法:①Kolosov-Muskhelishvili复势法[17],利用保角映射方法,外场解可表示为边界积分形式,然后外场进一步表示为Muskhelishvili复势的无限Laurent级数展开式[16];②外场的Eshelby张量法[13],利用了Eshelby等效夹杂法和内场的Eshelby张量的概念[2]。

复势法是解决二维Eshelby夹杂问题的有效方法,但是复势的保角映射方法和Laurent级数展开在实际应用中会得到渐近解或近似解。外场的Eshelby张量公式可以用闭合解形式表达[13],但是由于内部场的Eshelby张量表达式实际上是格林函数法中总应变卷积公式的特解[1],要把这些公式推广到外场,将会很复杂。因此,目前还没有二维Eshelby椭圆夹杂外部变形场的完全显式解析表达。

这就促使我们寻求一种解决二维椭圆异性夹杂外场问题的新方法。格林函数法在求解多种同性夹杂问题时既方便又直观[1,18],首先将无限平面固体中点状特征应变的复势解作为影响函数,通过格林函数法求出同性夹杂问题的复势。如果是异性夹杂,可进一步利用等效特征应变原理[19],将平面椭圆异性夹杂问题转化为相应的同性夹杂,再利用这些方法和已有的解,得到异性夹杂问题的复势[18,20],从而得到夹杂系统的显式解析解。

本研究目的是得到二维Eshelby椭圆夹杂外场的一般显式解析解,详细地揭示夹杂体内外弹性场的分布规律,为其在相关学科中的应用提供便利。首先利用等效特征应变原理求解具有均匀特征应变分布和远场载荷作用的椭圆异性夹杂内部场的应力分布,然后用复变格林函数法推导椭圆夹杂外部场的复势,最后进一步推导椭圆夹杂外部场的力学解。作为应用,分别研究受内压作用的液体夹杂和受远场纯剪切载荷作用的液体夹杂问题,以期解释土体液化的微观机理及液体夹杂对土体滑坡的影响。此外,对经典的Inglis椭圆孔问题[10]进行了分析,推导了其显式解析解,进一步证明本文所得一般显式解析解的优势。

1 具有均匀特征应变分布和远场载荷作用的椭圆异性夹杂

本节首先给出了具有均匀特征应变分布的椭球同性夹杂内部场的显式表达式及Eshelby张量,然后利用等效特征应变原理求解相应的椭圆异性夹杂问题,得到了椭圆异性夹杂的一般解。

1.1 具有均匀特征应变分布的椭球同性夹杂和Eshelby张量

对于如图2所示具有特定的均匀特征应变分布的椭球同性夹杂,根据Eshelby的结果[2],内部场的总应变可以表示为[1]

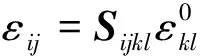
(1)

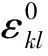
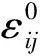
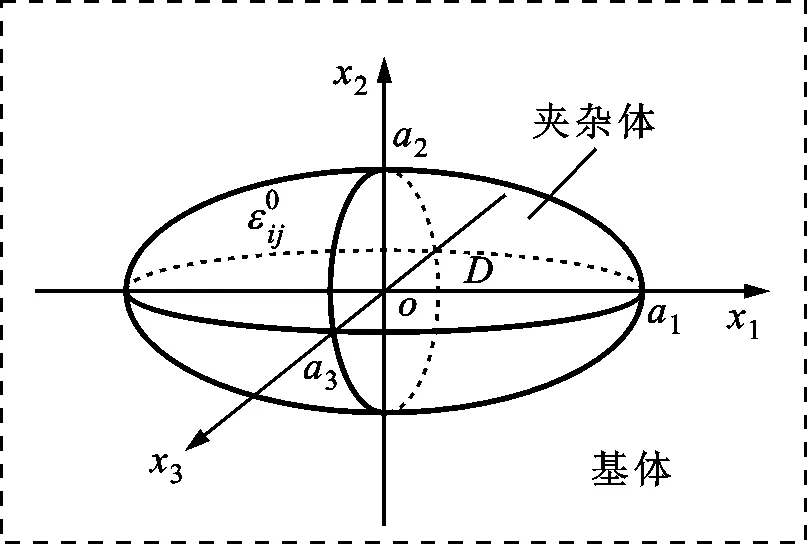
图2 具有特定均匀特征应变分布的椭球同性夹杂

令半轴长度a3趋于无穷大,经过复杂计算(参见附录A),得到式(1)的矩阵形式为

x∈D

(2)

式中:张量Sijkl为

(3)

式(2)的Eshelby张量的表达式可用于解决平面问题。

1.2 椭圆异性夹杂内部场的解

为了求解具有均匀特征应变分布的椭球异性夹杂问题,Eshelby[2]提出等效夹杂法,该方法证明了椭球异性夹杂问题可转化为椭球同性夹杂问题,如图3所示,后者适用于均匀材料,很容易解决。针对非椭球状夹杂和含非均匀特征应变分布的异性夹杂问题,Ma和Korsunsky[19]提出了基于虚功原理的等效特征应变原理,该原理能够解决具有任意非均匀特征应变分布的任意形状夹杂问题。

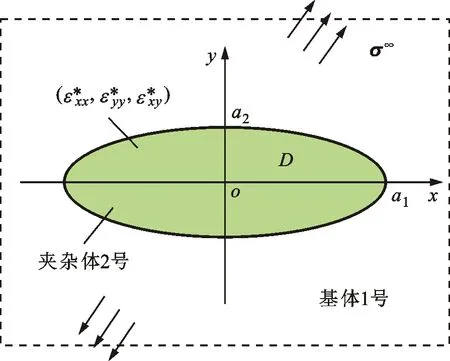
(a)原始异性夹杂系统

根据等效特征应变原理[19],可以将如图3(a)所示的具有均匀特征应变分布和远场载荷作用的椭圆异性夹杂问题,转化为如图3(b)所示的同性夹杂问题。这一原理要求图3(a)和图3(b)中的夹杂内部应力场和总应变场相同,由此可得异性夹杂-同性夹杂的变换方程为

C*(ε+ε∞-ε*)=C(ε+ε∞-ε0),x∈D

(4)

式中:C*和C分别为异性夹杂材料和基体材料的弹性常数;ε*为异性夹杂内部分布的真实特征应变;ε0为虚拟同性夹杂内的等效特征应变;ε∞为远场载荷且满足ε∞=C-1σ∞;ε为虚拟同性夹杂内的总应变。

需要注意的是,式(4)适用于任意几何形状的夹杂,而不仅仅局限于椭球形夹杂,总应变ε可以用卷积公式表示为[1]

(5)

式中:g表示格林函数(或影响函数),积分域为夹杂区域D。

对于各向同性材料

(6)

式中:λ、μ、λ1、μ1分别为基体和夹杂的拉梅常数。

式(4)中的矩阵可表示为

(7)

对于含均匀特征应变分布的椭圆异性夹杂,式(5)可简化为式(1),则等效特征应变可由式(4)直接求出

ε0=[C-(C-C*)S]-1[(C-C*)ε∞+C*ε*]

x∈D

(8)

或者

ε0=[C-(C-C*)S]-1[(C-C*)C-1σ∞+C*ε*]

x∈D

(9)

显然,此时得到的等效特征应变也是均匀的。

通过式(1)和式(9),夹杂内部应力场可表示为

σ=C(ε-ε0)+σ∞=C(S-I)[C-

(C-C*)S]-1[(C-C*)C-1σ∞+C*ε*]+σ∞

x∈D

(10)

夹杂外部应力场为

σ=Cε+σ∞,x∉D

(11)

式(11)只是一个形式解,其主要问题是如何求出应变ε的表达式。

在本节中,利用等效特征应变原理,将异性夹杂问题转化为相应的同性夹杂问题,得到具有均匀特征应变分布和远场载荷作用的椭圆异性夹杂的内部应力场表达式(10)。得到的等效特征应变表达式(9)将在下一节求解夹杂的外场时起关键作用。

2 Eshelby椭圆夹杂外部场的解

作为本文研究的核心,在这一节中,给出了位于无限平面固体中的点状特征应变的基本解,然后将其作为影响函数用格林函数法求解同性夹杂问题,导出了夹杂外部场的通解。

2.1 平面弹性体的Kolosov-Muskhelishvili复势公式

在平面弹性体复势公式[17]中,应力和位移的所有分量分别用两个势函数Φ(z)和Ω(z)表示

(12)

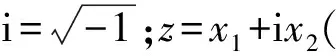
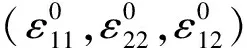
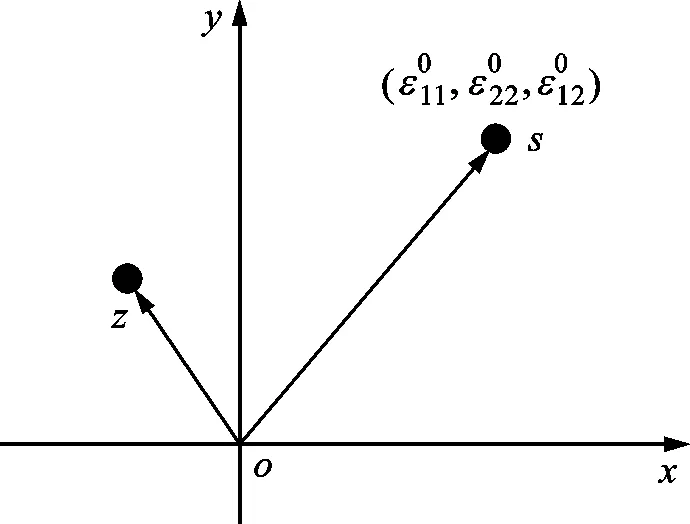
图4 无限平面固体中位于s处的点状特征应变

(13)

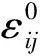
2.2 基于复变格林函数法的椭圆夹杂的复势

在图3(b)中,夹杂的等效特征应变和远场载荷会引起弹性变形。由于线弹性变形遵循叠加原理,因此同性夹杂中等效特征应变引起的应力势可通过复变格林函数法得到,其影响函数为式(13)。即通过对夹杂域D上的变量s=xs+iys进行积分,可得到由等效特征应变引起的夹杂外场的解

z∉D

(14)

其中Φs(z,s)和Ωs(z,s)即式(13)中的Φs(z)和Ωs(z)。

将式(13)代入式(14),再结合等效特征应变式(8)或式(9),可将式(14)转化为

z∉D

(15)

由于积分域为椭圆区域,式(15)中的积分可表示为

z∉D

(16)

此时式(15)转化为

z∉D

(17)

该结果适用于椭圆夹杂(a2≠a1),圆形夹杂的解可通过令式(17)中a2趋于a1得到

z∉D

(18)

将式(17)代入式(12),得到图3(b)中由等效特征应变引起的基体应力场,将式(17)计算的应力解与远场荷载相加,可得到外场的总应力解。式(17)是本研究获得的主要结果之一。

需要强调的是式(17)适用于夹杂物为线性连续介质,无论固体或液体。对于液体夹杂,只需让第一拉梅常数,即式(7)中的剪切模量μ1趋于0,第二拉梅常数λ1转换为液体的体积模量K1(K1=λ1),因此,压力与体积应变的关系仅由一个参数决定,不需要额外的假设[14-16]。此外,已有文献中的方法难以解决既承受压力又承受远场载荷的情况,而本节和第1节的公式可解决各种组合荷载条件下的问题。这种处理方法同时适用于固体夹杂和液体夹杂问题。

从计算过程可以看出,这种方法比之前提到的其他方法简便得多。在第3节中,将通过两种典型的液体夹杂情况进一步说明其优点,同时展示如何用本节中的解来处理具体问题。

3 加压椭圆液体夹杂的解

嵌于无限大弹性体中的加压椭圆液体夹杂模型的应用也很广泛,例如松散土体中的内部孔隙、嵌入页岩中的油或气穴。嵌于无限大平面固体中的加压椭圆液体夹杂模型如图5所示,针对嵌于无限平面固体中的加压椭圆液体夹杂,主要研究夹杂物周围的应力场,其典型背景包括水力压裂工程[21-22]和土体液化。

图5中液体夹杂内部压力为p0,夹杂区域用D表示。

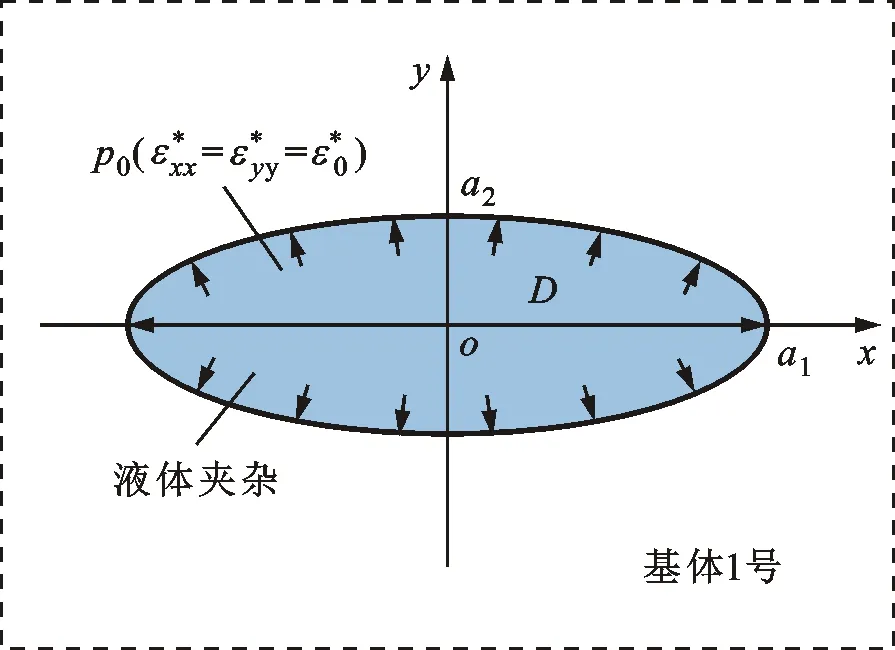
图5 嵌于无限大平面固体中的加压椭圆液体夹杂模型

(19)

然后,利用式(19),由式(9)求得等效特征应变表达式为

z∈D

(20)

最后,利用式(10)得到夹杂物中的应力分布为

σij=-p0δij=

z∈D

(21)

式中p0表示液体中的压力,p0为正值且满足

z∈D

(22)

(23)

根据式(23),可将式(17)转化为

z∉D

(24)

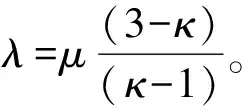
圆形夹杂的解由式(18)得到

(25)

将式(24)代入式(12),可得到夹杂外部应力场。为了能够更直观地反映应力分布情况,取ξ=a2/a1=0.3,κ=3-4ν=5/3,x和y坐标以主轴长度a1作无量纲化处理,得到如图6所示的具有内压p0的液体夹杂系统的无量纲应力分布。由图6可知:①无量纲应力σ11/p0和σ22/p0关于x轴和y轴对称,而应力σ12/p0关于x轴和y轴反对称;②在长轴端点附近会出现高度应力集中现象,

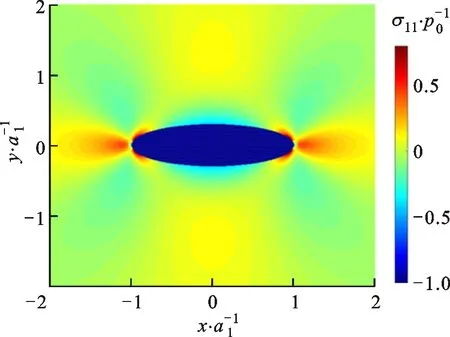
(a)σ11·p0-1

且σ22/p0的应力

集中远高于其他两个应力分量。

此外,σ22/p0较高的应力幅值表明其对系统影响更大,因此,应力σ22/p0沿x轴的分布(见图5和图6)可以由式(24)和式(12)推导得出

(26)

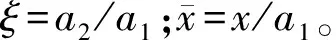
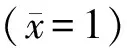
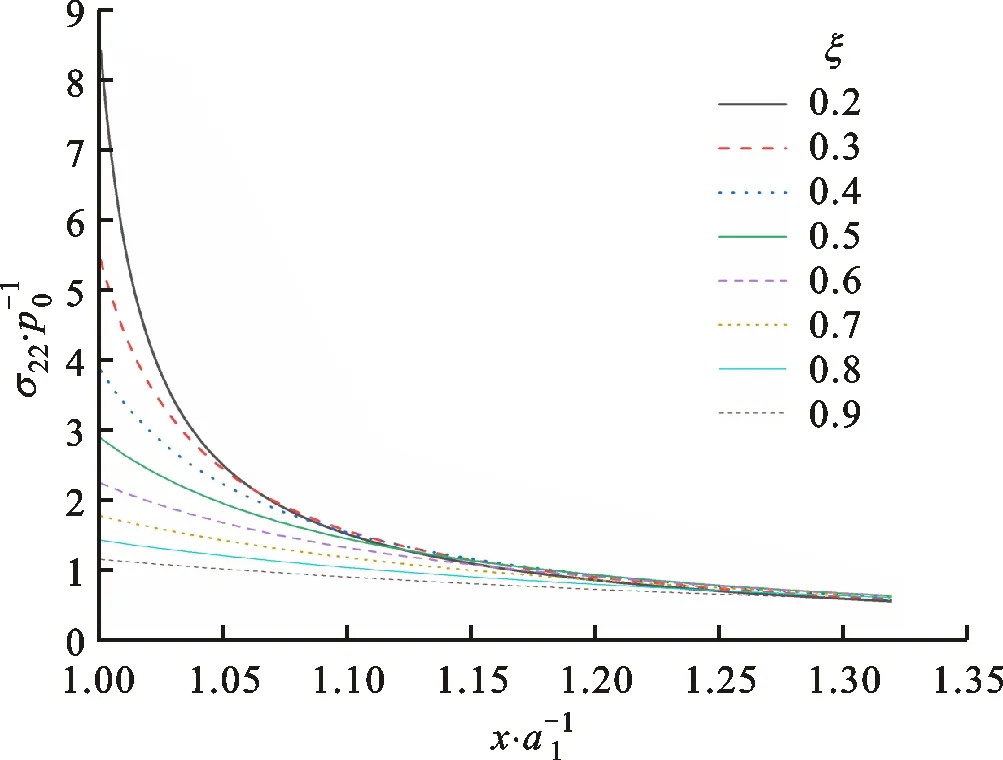
图7 不同纵横比ξ下外场σ22/p0沿轴的分布曲线

现有观点认为,土体液化是由于土体受到外力振动,原本松散的土体受到压缩,内部孔隙减小,导致空隙内水压升高,当水压升高至超过土体内承受的外部压力时,将产生土体液化[23-24]。本节的研究结果对土体液化提供一个新的机理解释,即靠近液体长轴端点处的土体应力集中,导致土体可能在该处因强度丧失而提早破坏,从而引起土体液化。

4 远场剪切载荷作用下的椭圆液体夹杂的解

在本节中,主要从两个方面对远场剪切载荷作用下的椭圆液体夹杂进行分析:Style等[14]的研究表明,小的液体夹杂能够增强软固体的刚度,然而,在宏观尺度上,液体夹杂对复合体系统剪切模量的影响还不可知;土体滑坡是土力学中的一个重要研究课题,其由剪切载荷引发[25-26],但是针对含有液体的土体滑坡问题研究很少,微观力学分析可能会为该问题提供一些新的研究思路。

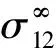
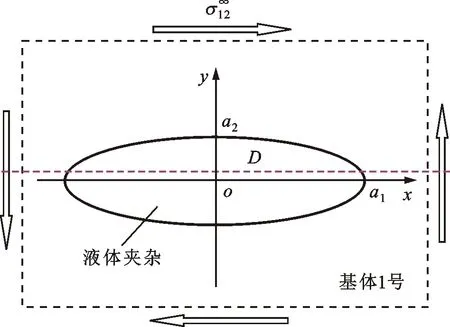
图8 嵌于无限弹性平面固体受远场剪切载荷作用的椭圆液体夹杂

4.1 远场剪切载荷作用下的椭圆液体夹杂内部应力场

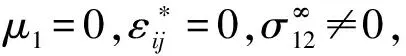
(27)

由式(10)得到夹杂内的应力为

σij=0,x∈D

(28)

这表明,液体夹杂不承受远场剪切载荷,因此,远场剪切载荷将被重新分配并完全施加在基体材料上,导致系统产生较大的剪切变形,或者可以理解为液体夹杂的存在会减小复合系统的整体剪切模量。

4.2 远场剪切载荷引起的复势

结合式(27),式(17)可转化为

z∉D

(29)

式中λ=μ(3-κ)/(κ-1)。

将式(29)代入式(12),并结合远场载荷将得到应力场。同样,圆形夹杂的解由式(18)得到

(30)

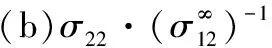
x

y

x

y

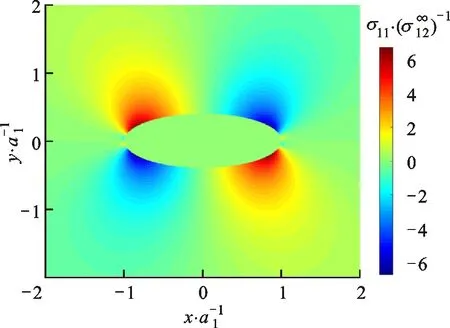
由式(29)可以看出,随着长短轴纵横比ξ的减小,应力集中向长轴(x轴)的端点移动。图8中外场沿x轴的剪切应力可表示为

(31)

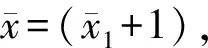
(32)

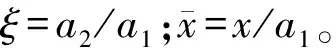
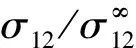
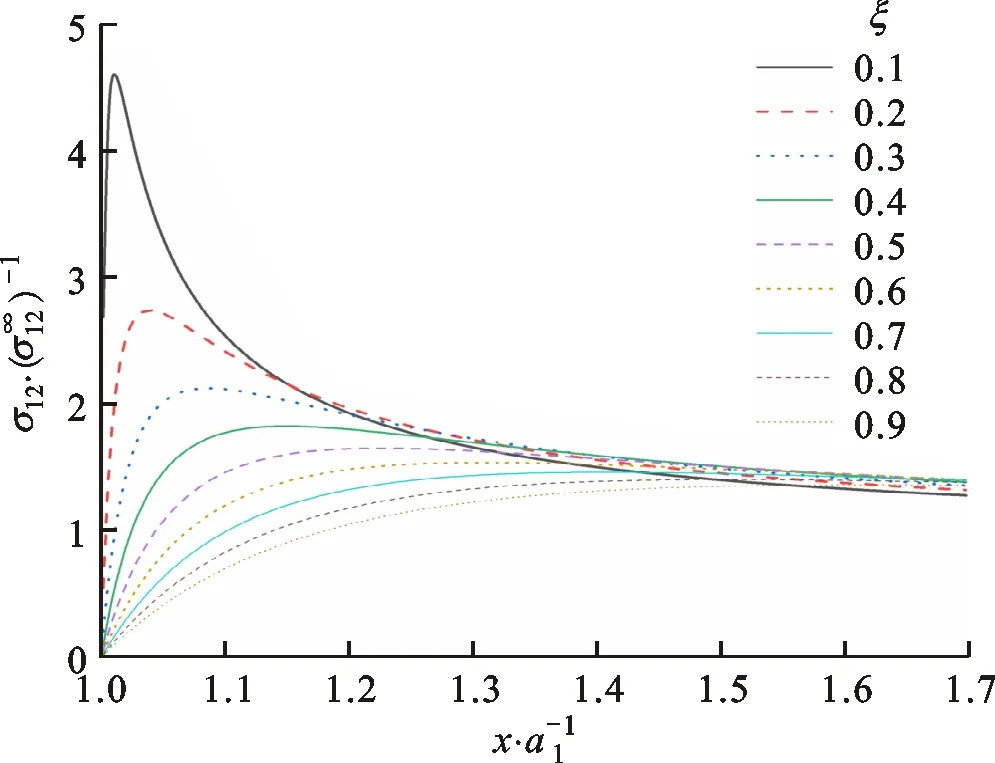
图10 不同纵横比ξ下的受远场剪切载荷作用夹杂外沿轴的无量纲剪应力曲线

可以发现,本节中的公式并未涉及液体性质,这意味着液体夹杂在这种载荷条件下相当于一个空腔。实际上,该解与椭圆孔在远场剪切载荷作用下的解相同,受远场剪切载荷作用的细长形液体夹杂将导致夹杂周围产生应力集中,从而可能破坏基体。

研究表明:土体滑坡是滑坡体中存在宏观剪切作用,导致某个面的剪应力达到抗剪承载力、引发相对滑动。本节的研究结果对含有液体的土体滑坡提供一个新的机理解释,即液体夹杂的存在减小了系统整体的剪切模量,且在远场剪切载荷作用下,靠近液体长轴端点处的土体发生应力集中,因此对于含有液体的土体滑坡问题,液体夹杂的存在会促进滑坡的提早发生。

5 远场拉伸载荷作用下Inglis椭圆孔问题的解

1913年,Inglis发表了椭圆孔受远场外力的以级数表达的渐进解[10]。需要指出的是,Inglis的解和Griffith裂纹表面能概念的提出开启了断裂力学的新纪元。由于Inglis解是在曲线坐标系下表达的,不便于使用,因此在本节中通过对这一问题重新研究,获得其直角坐标系下的显式解析解简洁形式。

对于如图11所示在无限大板受远场拉伸载荷作用下的椭圆孔问题,式(7)转换为

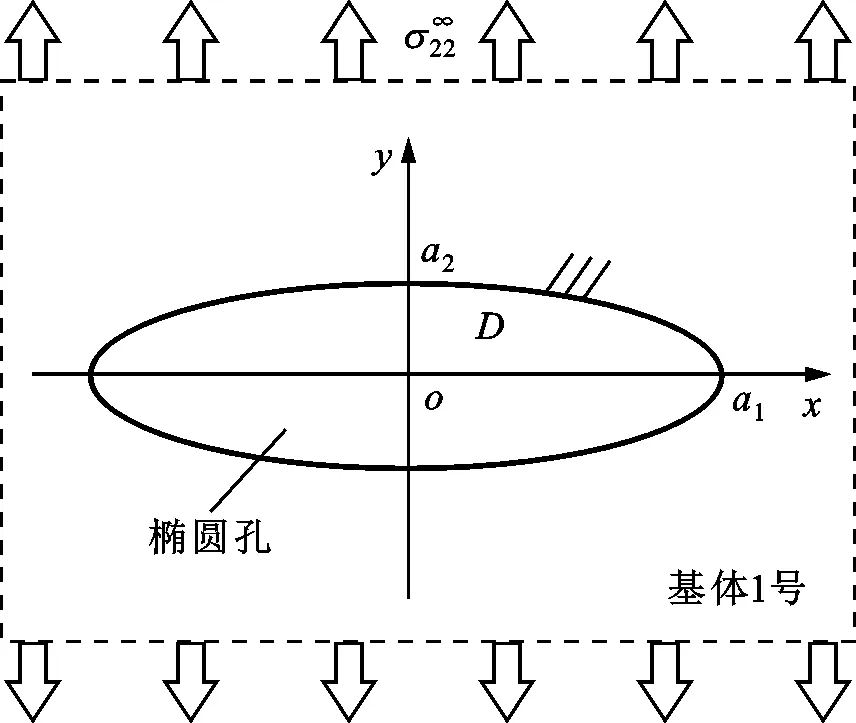
图11 嵌于无限大固体中受远场拉伸载荷作用的Inglis椭圆孔

(33)

同样,等效特征应变由式(9)得到

x∈D

(34)

结合式(9)和式(33),由式(10)得到椭圆孔中的应力分布为

σ=C(S-I)ε0+σ∞=

C(S-I)(C-CS)-1σ∞+σ∞=0,x∈D

(35)

这也验证了之前的推导。

根据式(34),式(17)转换为

z∉D

(36)

式中λ=μ(3-κ)/(κ-1)。

圆形夹杂由式(18)得到

z∉D

(37)

将式(36)代入式(12),得到由等效特征应变引起的基体应力场,总应力由基体应力场加上远场载荷σ∞得到。相比较Inglis的渐进解,此处给出的解是一种通用形式,适用于平面应变(κ=3-4ν)情况和平面应力(κ=(3-ν)/(1+ν))情况,ν为泊松比。

6 结 论

异性夹杂力学是一个经典的固体力学问题,它的应用意义不言而喻,但是对其的研究仍存在很多不足。本文主要研究了二维Eshelby椭圆异性夹杂的外场问题。利用等效特征应变原理和复变格林函数法,得到了具有均匀特征应变分布的Eshelby椭圆异性夹杂在远场载荷作用下内外场的一般显式解析解。

本文特别探讨了它在液体夹杂问题中的应用,并将液体夹杂和固体夹杂统一到Eshelby夹杂力学框架内。研究表明,液体夹杂中的内压会导致长轴端点处产生严重的应力集中,从而为土体液化提供了一个新的机理解释。此外,在纯剪切荷载作用下,剪切应力集中并不完全产生在长轴端点处,而是在端点附近,并且液体夹杂的存在会减小系统整体的剪切模量,这一研究揭示了液体夹杂对土体滑坡的影响。最后,重新研究了著名的Inglis椭圆孔问题,并给出了其在直角坐标系下的显式解析解。

本文得到的Eshelby椭圆异性夹杂问题的一般解析解更简洁,期望它能为解决不同学科中的一系列Eshelby椭圆异性夹杂问题提供参考。