多翼离心风机分组优化设计对风机盘管整机气动性能的响应度研究

2022-07-19刘阳刘小民陈宗华席光

西安交通大学学报 2022年7期

刘阳,刘小民,陈宗华,席光

(1.西安交通大学能源与动力工程学院,710049,西安;2.西安泛仕达流体机械有限公司,710075,西安)

风机盘管广泛应用于大型商场、办公楼等大型中央空调系统中,内部搭载的多翼离心风机常为双风机或三风机并联布置,可以实现中短距离的风管送风,因其安装灵活、装修隐蔽,很多家庭住宅也普遍采用中央空调风管系统,这对风机盘管整机的气动性能和噪声性能提出了更高的要求。整机的性能优化通常以单风机为基础,但是整机内部空间受限,流动阻力增加,使得单风机优化效果并不能有效体现在整机上。因此,将多翼离心风机各部件进行分组优化,研究其对整机性能变化的响应度,并以此为依据采取针对性的优化对于提升风机盘管整机的性能具有重要的理论意义和实际应用价值。

叶轮、集流器和蜗壳是多翼离心风机的重要结构和功能部件。叶轮在运行过程中与静止部件发生干涉,在旋转、黏性和逆压梯度作用下,多翼离心风机内部流动呈现出复杂的三维、黏性、非定常、非均匀特征[1]。多翼离心风机中叶轮叶片多为前向弯曲叶片,流道弯曲且狭小,受叶片壁面逆压梯度影响,在叶片吸力面更易产生流动分离。这种分离涡进入蜗壳流道,还会诱导不稳定的气动噪声,且上游叶片产生的尾迹对下游通道中的气流运动也存在较大的激励作用[2-3]。Darvish等[4]研究了叶片数和出口角对多翼离心风机气动性能的影响,结果表明叶片数和出口角的增加会减弱叶轮流道内的流动分离。Zhou等[5]利用改进的Hicks-Henne函数对多翼离心风机叶片中弧线进行参数化设计,得到了曲率平滑的叶片型线,叶片进口区前缘涡数减少,风机的总压效率和流量显著提高,但是该函数并不能对叶片弦长参数进行优化。Wang等[6]研究了叶片全切割和部分切割对多翼离心风机气动性能的影响,发现适当的叶片切割能使前盘附近的非活动区范围减小,风机在总压效率和静压升方面有较大的提升。对非等厚翼型叶片而言叶片切割会破坏叶片前缘结构,导致气动性能下降。Lin等[7]对叶片翼型进行了研究,将低速NACA4412翼型应用在多翼离心风机的叶片设计中,发现设计的翼型叶片有效缓解了叶片吸力面的流动分离,有利于风机效率的提高。王梦豪等[8]将鸮翼截面翼型进行仿生重构应用到离心风机叶片上,发现仿鸮翼叶片能够有效抑制通道内漩涡流的产生与发展,降低叶片前缘区域和蜗舌区域的压力脉动。

集流器和蜗壳是风机中的静止部件,与叶轮存在着较强的交互效应和匹配关系。由于叶轮与集流器存在间隙,叶轮出口侧的高压气流将通过该间隙回流到叶轮进口的低压区,形成泄漏,引起损失[9]。Liu等[10]提出了一种非对称的D型集流器,研究表明该集流器可有效抑制低流量系数下蜗舌处集流器进口的回流现象,风机性能获得明显提升。杨伟刚等[11]提出了一种偏心集流器,发现偏心方向对应叶道内的流动分离减弱,叶轮前盘和集流器间隙的流量泄漏减小。王嘉冰等[12]研究了3种不同结构形式的集流器对柜式空调用多翼离心风机的性能影响,得出集流器出口直径大于叶轮内径的收敛型集流器能使风机的气动性能达到最优。温选峰等[13]的实验结果表明,具有合理参数和安装位置的椭圆形集流器能够有效提高多翼离心风机的整体气动性能。

蜗壳内部存在着多体扰流问题,受逆压梯度影响,还会在蜗壳通流截面形成与气流主流方向垂直的二次流,造成蜗壳内部气流的冲击[14-15]。由于各种流动损失的存在,理论蜗壳型线设计方法并不一定满足实际的运行状况,且目前多翼离心风机的使用越来越倾向于小型化,这就对尺寸限制条件下的传统蜗壳型线的设计提出了挑战。受蜗壳结构的影响,叶片出口周期性的尾流与叶片表面的分离流动会激励与蜗舌之间的非定常干涉作用,对蜗舌造成较大的冲击。蜗舌附近的脉冲压力导致蜗舌区域出现严重的回流,不仅影响风机的风量,也是风机离散噪声的主要噪声源[16]。Wen等[17]的实验结果表明,由于蜗壳切割破坏了蜗壳流场的连续性,风机全压和效率明显下降。蒋博彦等[18]在蜗壳单侧切割的基础上提出了一种等比例组合式切割方案,该方案可有效削弱单侧切割深度过大对风机性能的负面影响。王军等[19]为了解决切割蜗壳型线造成多翼离心风机气动性能下降的问题,在尺寸限制下采用二次非均匀B样条曲线表征蜗壳型线,通过NSGA-II算法对其进行多目标优化。Zhou等[20]基于部分相干分析对多翼离心风机蜗舌形式进行了多目标参数优化,减少了蜗舌区域压力脉动向其他区域的传递,有效提升了风机的气动性能。Wang等[21]提出一种倾斜仿生蜗舌,风机内部的轴向流场随着叶轮前盘非活动区尺寸的减小变得均匀,叶轮与蜗舌的相互作用得到了明显改善。Wu等[22]提出了一种波形仿生蜗舌,风机内部涡流的强度和规模得到抑制,有效降低了叶轮出口气流与蜗舌之间的相互作用。

上述针对多翼离心风机叶片、蜗壳型线、蜗舌形式以及集流器的优化能够有效改善风机内部流动状态,提升风机的气动性能,但是并未研究整机状态下实际的优化效果和流动特性,且在优化过程中没有考虑到各动静部件之间的协同匹配效果,因此本文采用分组流程设计的方法分别对多翼离心风机中的叶片、蜗壳型线、集流器和蜗舌进行优化。首先采用3阶贝塞尔曲线拟合等厚叶片中弧线,建立相关优化变量和目标响应的Kriging模型,再采用NSGA-II算法求解Pareto前沿,在此中弧线基础上构造吸力面仿鱼形叶片,之后对偏流蜗壳型线、蜗舌形式和外凸集流器分别进行优化设计。以风量作为主要参数,引入系数ε表征单风机性能变化对整机气动性能变化的响应度,在每一步优化过程中对整机性能进行响应度判断,最大限度地提升风机盘管整机的气动性能。

1 数值计算

1.1 物理模型

本文的研究对象为风机盘管和其内置的双吸式多翼离心风机,双风机并联布置,蜗壳和电机固定在整机箱体上,叶轮通过中间电机轴悬臂连接。整机采用下回风进气方式,从蜗壳出口吹出气流经过V型换热器流出,风机盘管结构如图1所示。

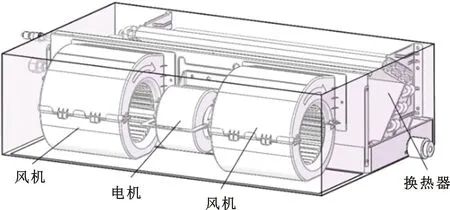
图1 风机盘管结构示意图

风机由蜗壳和叶轮两部分组成,叶轮设有固定中盘,中盘两侧叶轮宽度比为1∶1,叶片为前弯形式,双吸式多翼离心风机结构如图2所示。取蜗壳内壁型线建立蜗壳区域流体域。风机叶轮为塑料叶轮,考虑到叶片存在一定的拔模斜度,建立叶轮流体域时选取叶顶处叶片型线,前盘装有的环形箍主要为保证叶片强度,对气动性能影响很小,因此建模时将环形箍去除。原型多翼离心风机叶轮和蜗壳主要结构参数如表1所示。

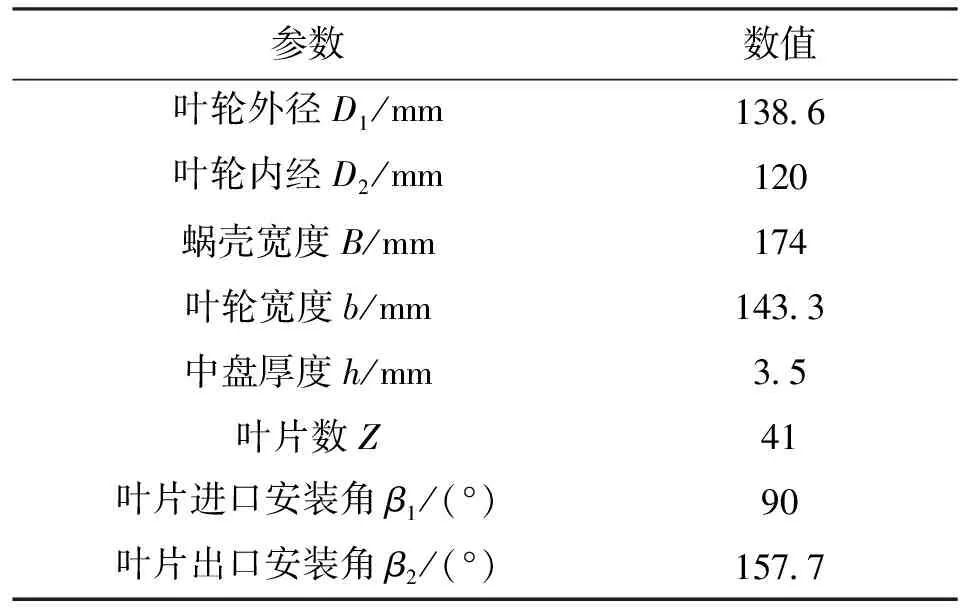
表1 原型多翼离心风机叶轮和蜗壳基本结构参数

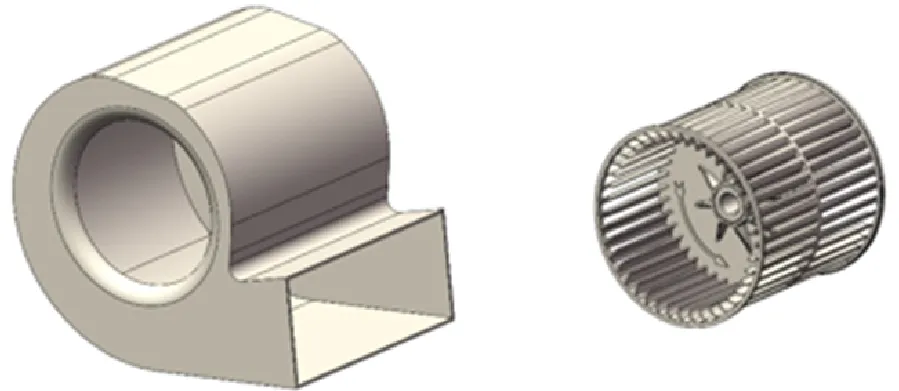
(a)蜗壳 (b)叶轮

1.2 多翼离心风机计算模型

根据图2所示的风机模型建立风机的计算流体域模型,主要分为蜗壳区、叶轮区、进口延伸段和出口延伸段,为使计算具有更好的收敛性,延伸段的长度设置为2.5倍叶轮外径。对各部分进行网格划分,采用非结构化网格,并在近壁面和叶片前后缘进行了加密处理,固体近壁面y+保持在30～100之间,各部分通过interface面连接,双吸式多翼离心风机数值计算模型如图3所示。

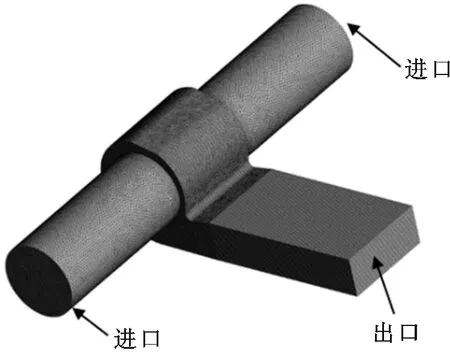
图3 双吸式多翼离心风机数值计算模型

采用Fluent求解器对多翼离心风机内部流场进行数值模拟计算。在流场计算中,流动控制方程为黏性不可压缩雷诺时均Navier-Stokes方程,湍流模型采用Realizablek-ε模型,近壁面处理采用标准壁面函数,压力速度耦合采用SIMPLE算法,动量方程、能量方程和湍流耗散方程均采用二阶迎风格式。进口边界条件给定总压为0 Pa,出口边界条件给定静压为0 Pa。将叶轮区设置为旋转区域,采用多参考系模型,设定转速为1 120 r/min,收敛残差为10-4。

为保证计算结果的准确性,对网格进行无关性验证,如图4所示,最终确定总网格数为364万,叶轮和蜗壳网格数分别为219万和97万。

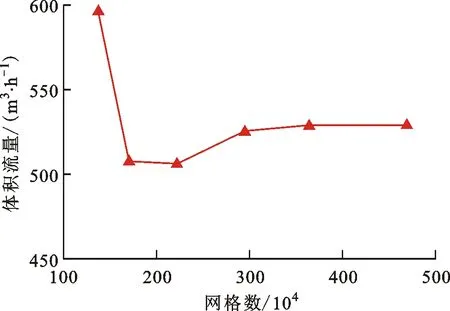
图4 网格无关性验证

1.3 风机盘管计算模型

根据图1所示的风机盘管整机结构建立整机计算流体域模型,主要分为箱体段1、箱体段2、蜗壳区、叶轮区、换热器、进口延伸段和出口延伸段,延伸段的长度设置为2.5倍叶轮外径。网格划分方式和计算方法与单风机基本一致,风机盘管整机数值计算模型如图5所示。换热器为V型翅片管式换热器,在计算时采用多孔介质模型[23]代替,多孔介质模型阻力系数计算公式如下

图5 风机盘管整机数值计算模型

ΔP=av2+bv

(1)

a=C2ρh/2

(2)

b=μC1h

(3)

式中:ΔP为换热器前后压降;v为换热器处气体流速;h为换热器厚度;C1为黏性阻力系数;C2为惯性阻力系数。

式(1)为实验测试得出的压降和速度函数关系,联立式(1)～(3),可计算出C1和C2。空气的物性参数取15 ℃常压状态下,μ=1.789 4×10-5kg/(m·s),ρ=1.225 kg/m3,孔隙率取0.98。将叶轮区设置为旋转区域,采用多参考系模型,设定转速为1 120 r/min,收敛残差为10-5。

1.4 实验测量

气动性能测试按照GB/T 1236—2000《工业通风机用标准化风道进行性能试验》测试,系统主要由试验风机、风室、辅助风机以及数据采集系统组成。测量时根据喷嘴的流速选择合适的喷嘴直径,经数据采集系统得到风机的流量。风机和风机盘管气动性能测试装置如图6所示。

(a)风机 (b)风机盘管

图7给出了多翼离心风机实验和模拟性能曲线。由图7可知,数值模拟的工况点与实验测量的数值吻合较好,在0 Pa静压的工况下,风机最大风量模拟值和实验值分别为529.2、548.5 m3/h,相对误差为3.52%,整机最大风量模拟值和实验值分别为674.6、673.1 m3/h,相对误差为0.23%,皆在工程允许的5%以内,证明了本文所建立的数值计算模型的有效性。

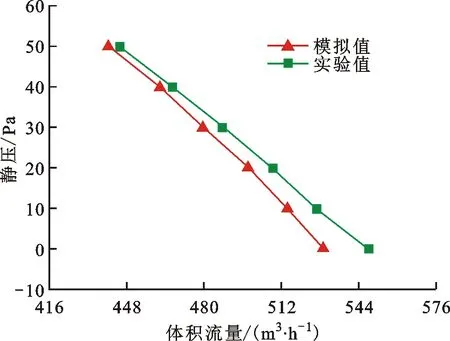
图7 多翼离心风机实验和模拟性能曲线

2 优化设计方案

针对多翼离心风机的动静部件,对叶轮、蜗壳型线、蜗舌和集流器进行了4个参数的分组优化设计,并对优化之后的单风机进行整机计算,研究其对整机性能的影响。本文以风量作为性能标准,判断单风机性能变化对整机性能变化的响应度大小,如果整机性能变化响应度为负值,则放弃该优化步骤,在上一步优化的基础上进行下一步优化。图8为多翼离心风机分组优化设计流程图。

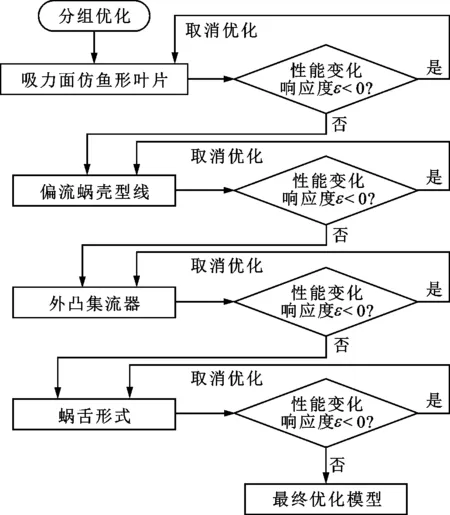
图8 多翼离心风机分组优化设计流程图

2.1 吸力面仿鱼形叶片设计

多翼离心风机的叶片具有强烈的前向弯曲特性,叶片吸力面极易发生流动分离。基于贝塞尔曲线的灵活弯曲特性和鱼体前缘吸力机制[24],提出了一种吸力面仿鱼形叶片设计方法,图9为吸力面仿鱼形叶片优化设计流程图。

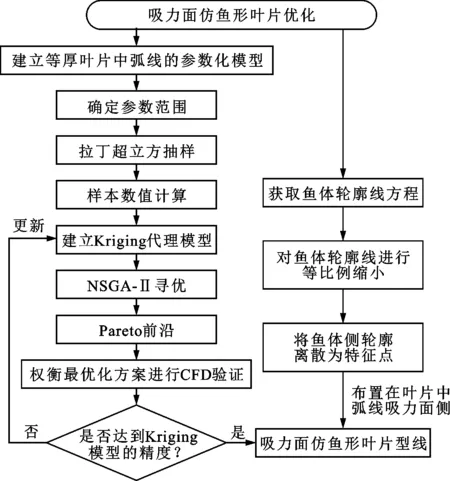
图9 吸力面仿鱼形叶片优化设计流程图

首先对原型叶片中弧线进行优化设计,等厚叶片中弧线的几何参数化如图10所示,采用3阶贝塞尔曲线拟合叶片中弧线,共4个控制点(V1～V4),其中V1点固定。V2点以叶片进口安装角β1和长度L1为控制参数,V3点以出口安装角β2和长度L1为控制参数,V4点在叶轮外径上圆周移动,以叶片中心角γ1为控制参数。抽样策略采用拉丁超立方进行设计。各设计参数的取值范围为:β1=45°～80°,L1=4～7 mm,β2=160°～175°,L2=3～6 mm,γ1=3.5°～5.8°。基于Isight[25]视觉设计平台生成50组单圆弧等厚叶片方案。

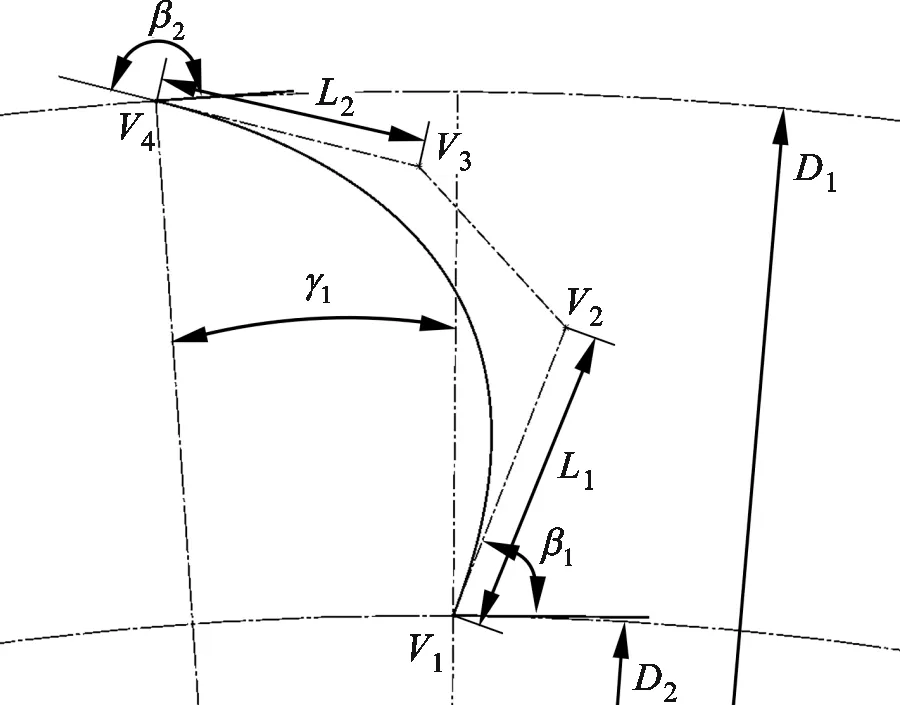
图10 等厚叶片中弧线的几何参数化

通过CFD计算,以最大流量和总压效率为响应变量构建Kriging模型,本文利用设计空间[26]中任意样本点的相对误差和平均相对误差来验证Kriging模型的准确性,随机选取5组样本验证Kriging模型,各样本响应值的相对误差均小于5%,精度满足给定的工程要求。采用NSGA-II算法进行多目标优化,选择父代群体交叉概率为0.9,种群代数为20,种群数量大小设置为400,交叉和变异分布指数默认设置为10.0和20.0。图11给出了等厚叶片多目标优化的Pareto前沿,最大流量和总压效率具有相同的权重,最优方案风量为554.4 m3/h,总压效率为61.21%,基于此最优叶片中弧线设计参数对叶片进行仿生重构。

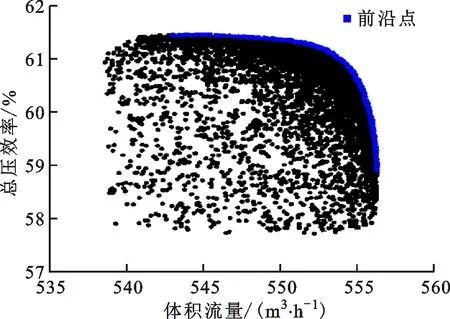
图11 等厚叶片多目标优化的Pareto前沿

本文选取鲹科鱼类的头部到尾柄处轮廓构造仿生叶型,鱼体轮廓特征结构的提取参考文献[27],鱼体水平剖面的轮廓线方程如下式

(4)

图12给出了鱼体水平剖面结构,从头部到尾部依次为椭圆形线、抛物线和直线。首先对鱼体轮廓进行比例缩小,尾部直线部位存在尖点,并不能将鱼体中弧线缩小到同样叶片中弧线长度。图13为吸力面仿鱼形叶片设计参数结构图,α1为叶片中弧线所对应的圆心角,α2为叶片压力面轮廓线所对应的圆心角,将叶片的中弧线延长至α2所对应的弧长,鱼体中弧线缩小至α2所对应的叶片中弧线弧长,然后将缩小的轮廓线离散为特征坐标点(x,y)。将鱼体单侧轮廓特征点布置在叶片中弧线吸力面侧,通过样条拟合曲线连接,压力面型线保持原单圆弧等厚型线,尾缘超出叶轮外径的阴影区域切除,形成吸力面仿鱼形叶片。

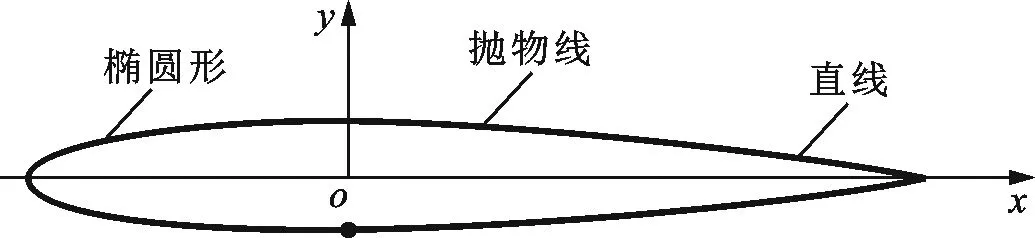
图12 鱼体水平剖面结构

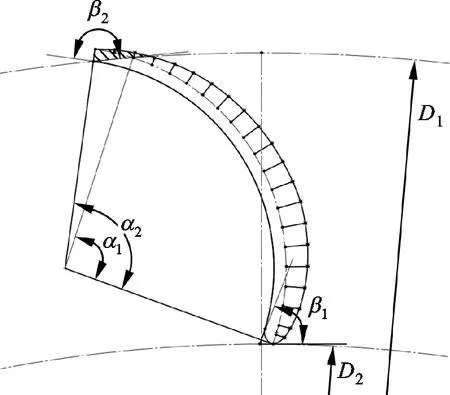
图13 吸力面仿鱼形叶片设计参数结构图

2.2 偏流蜗壳型线设计

原蜗壳型线在90°方向上有切割,这种不连续的蜗壳型线会与叶轮形成不合理的相互作用,蜗壳表面静压出现明显的突变。本文采用文献[17]提出的一种偏流蜗壳型线设计方法。该方法主要是通过阻断蜗舌附近叶片流道内的流动,以保持其余叶片流道内的正常流动状态。蜗壳型线由圆弧线和螺旋线两部分组成。与叶轮同心的弧线从φv的滚动角开始,止于阻塞角φblock处。在这一片圆弧区域阻碍叶片流动,蜗壳螺旋展开角θ的角度从φblock到360°,θ=5.4°。通过控制φblock和t的大小确定蜗壳型线,保证蜗壳的出口扩张度,蜗舌半径和蜗舌间隙不变。本文选择设计参数t=8.5 mm,φblock=144°,偏流蜗壳型线设计示意图如图14所示。蜗壳型线控制方程如下式

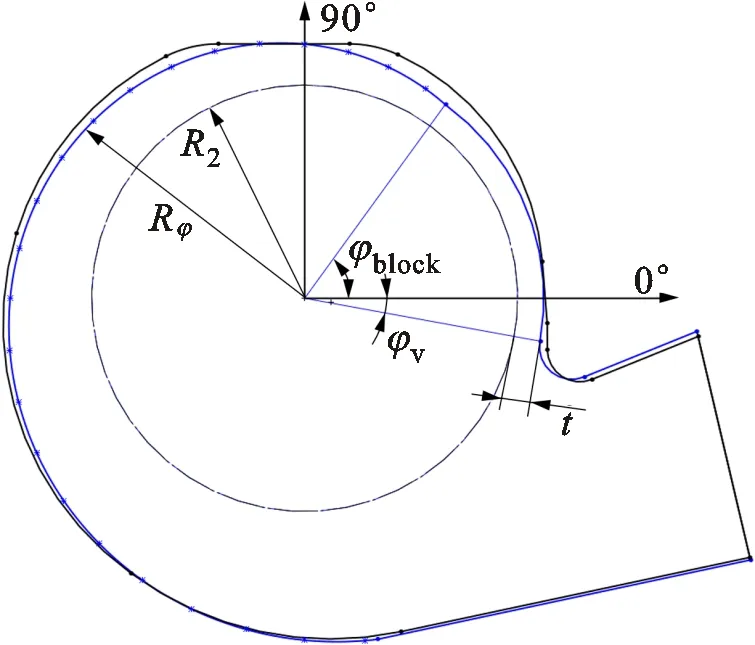
图14 偏流蜗壳型线设计示意图

Rφ=R2+t,φ∈[φv,φblock]

(5)

Rφ=(R2+t)e(φ-φblock)tanθ,φ∈(φblock,2π]

(6)

2.3 外凸集流器设计

集流器的主要结构参数有轴向间隙δ、集流器出口直径do和集流器高度s。本文对外凸集流器采用外凸设计,如图15所示。凸出距离l=5 mm。为保证集流器间隙不变,叶轮单侧高度分别增加5 mm。

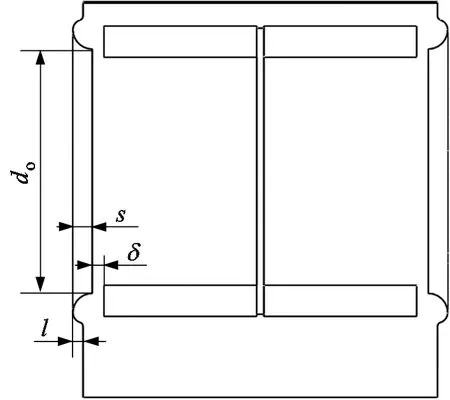
图15 外凸集流器设计示意图

2.4 蜗舌形式设计

蜗舌的深浅对风机的性能有很大的影响,原型蜗舌与叶轮出口气流接触的相切位置夹角定义为φα,φα=17.17°,优化之后φβ=13.41°,设计过程中保持蜗舌间隙、蜗舌半径和出口扩压度不变,蜗舌形式如图16所示,由原来的深舌变为浅舌。

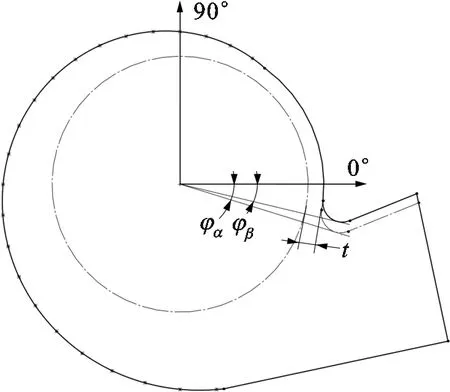
图16 蜗舌形式设计示意图

3 数值计算结果及分析

3.1 计算结果

对各方案采用上文所述的数值计算模型进行单风机和整机分组优化设计模拟,数值计算结果见表2和表3。

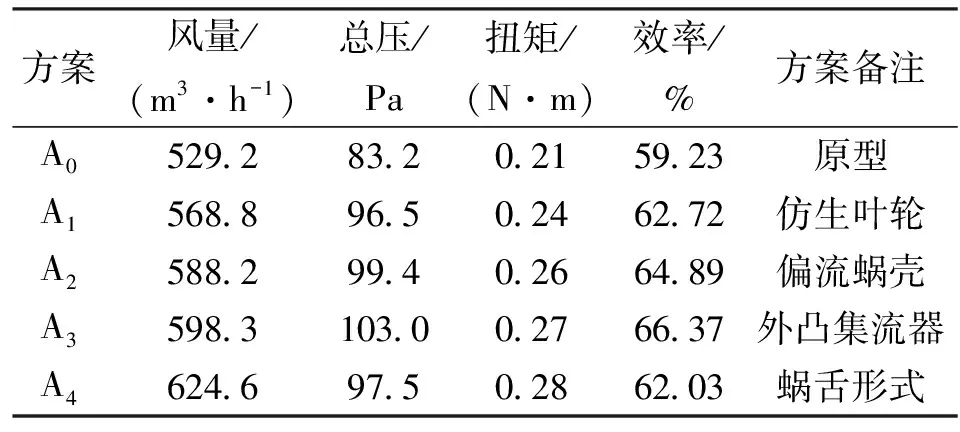
表2 单风机分组优化设计模拟结果

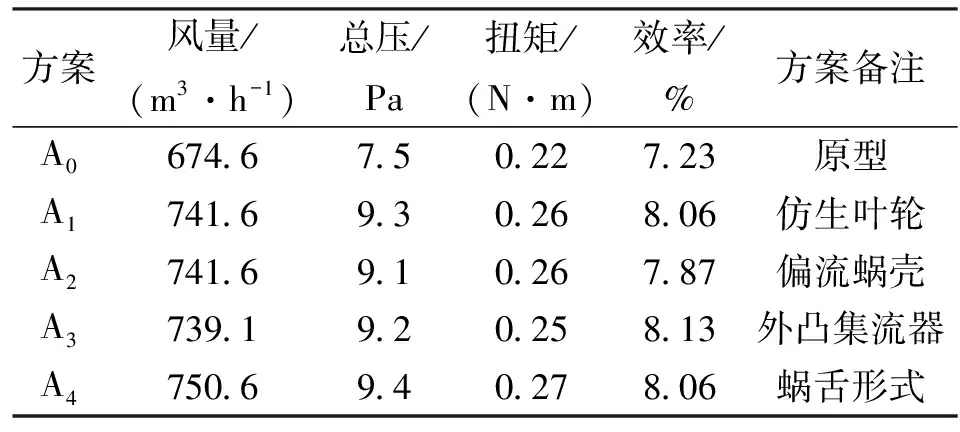
表3 整机分组优化设计模拟结果

风机效率的计算公式如下

(7)

式中:P为出口总压;Q为质量流量;n为转速;M为扭矩。

表2为单风机分组优化设计模拟结果,由表2可以看出,最终优化方案A4相比于原型获得了最大的风量提升,风量提升18%,但是效率相较于前一方案反而有所降低。根据式(7),在转速一定的情况下,风机的效率主要受出口总压、风量和扭矩3个因素影响,其中与出口总压和风量是正相关,与扭矩是负相关。在2.4节中,蜗舌形式由原来的深舌变为浅舌,为保证出口扩压度不变,蜗壳出口面积有所增加,导致出口流速减小,动压减小,出口总压随之减小。因为风量增加,所以叶轮扭矩增加。虽然蜗舌形式的变化使得风量有所上升,但是并没有弥补总压降低和扭矩增加带来的损失,所以效率有所降低。

且由表2可以看出,各方案的扭矩逐渐增加,原因在于各方案对单风机而言风量都有所提升,叶轮的做功能力变强,功耗增加。经过分组优化设计,蜗舌形式的变化是在之前所有有效方案的基础上进行的优化,相对于原型有最大的风量提升,因此扭矩最大。

表3为整机分组优化设计模拟结果,每组优化方案都是在前一组优化方案有效的基础上进行的,对比表2和表3,发现各组优化方案对于单风机和整机的性能提升并不完全一致。A1方案对于单风机和整机而言风量效率都有明显的提升。A2方案对于单风机而言风量和效率有所提升,但是对整机而言风量并没有提升,效率也有所下降。风量作为用户关注的主要性能指标,为简化问题,本文以风量作为主要参考,将优化方案与前一方案进行对比,验证单风机不同优化结构对整机性能变化的响应度。μz为整机风量变化的百分比,μd为单风机风量变化的百分比,两者比值εn表征单风机性能变化对整机性能变化的响应度

(8)

式中:n=1,2,3,4;x为前一组有效方案的编号。

表4为单风机和整机的性能变化对比,由表4可以看出,方案A1的ε1=1.33,单风机叶轮的修改对整机性能变化的响应度最大。

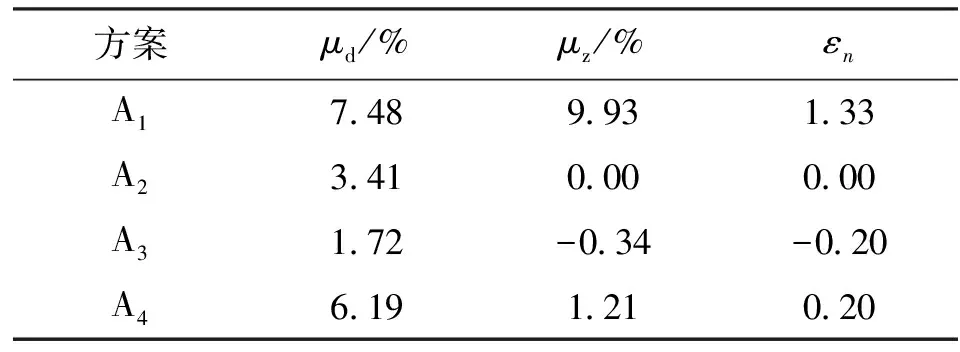
表4 单风机和整机的性能变化对比

本文研究的风机盘管为双风机内置,理论上单风机的性能提升应带来双倍的整机性能提升,即最大理论值εth=2,但是由于双风机并联以及整机内部流动阻力的影响,使单个风机的工况向小流量点偏移,因此并不能达到理论值。μd1=7.48%,μz1=9.93%,明显大于其他方案,说明对叶轮进行正确的优化能够有效提升多翼离心单风机和风机盘管整机的性能;ε2=0,μd1=3.41%,说明虽然偏流蜗壳型线对单风机的性能提升效果为3.41%,但是对整机性能的变化几乎没有影响;ε3=-0.2为负值,μd3=1.72%,μz3=-0.34%,说明外凸集流器的设计虽然能够提升单风机的性能,但是对整机的性能反而起到了反作用,这主要是由于外凸集流器凸出的部分使整机的进气条件恶化,导致整机风量下降,因此在优化过程中取消该优化方案,蜗舌的优化依然以第二步优化为基础;ε4=0.2,系数较小但是也为正值,说明单风机蜗舌形式的变化对整机的性能有提升效果但是并不明显。主要是由于蜗舌形式发生变化之后,蜗壳的出口总压降低,导致搭配整机运行的时候,由于系统阻力增加,风机的抗静压能力不足,单风机所带来的风量提升并不能明显的体现在整机上,ε4也仅为0.2。

3.2 内部流场分析

为了进一步探究多翼离心风机内部各动静部件之间的协同匹配效果以及分组优化设计对应整机的流动状态,通过数值模拟的方法分别对单风机和整机进行内部流场分析。图17为风机盘管整机观测截面位置示意图,S1截面位置为双风机中电机侧叶轮的50%叶高截面,S2截面位置为图2(c)中的A-A截面所在位置,S3截面平行于整机出口气流方向,截面位置远离整机进口方向偏移叶轮中心40 mm。

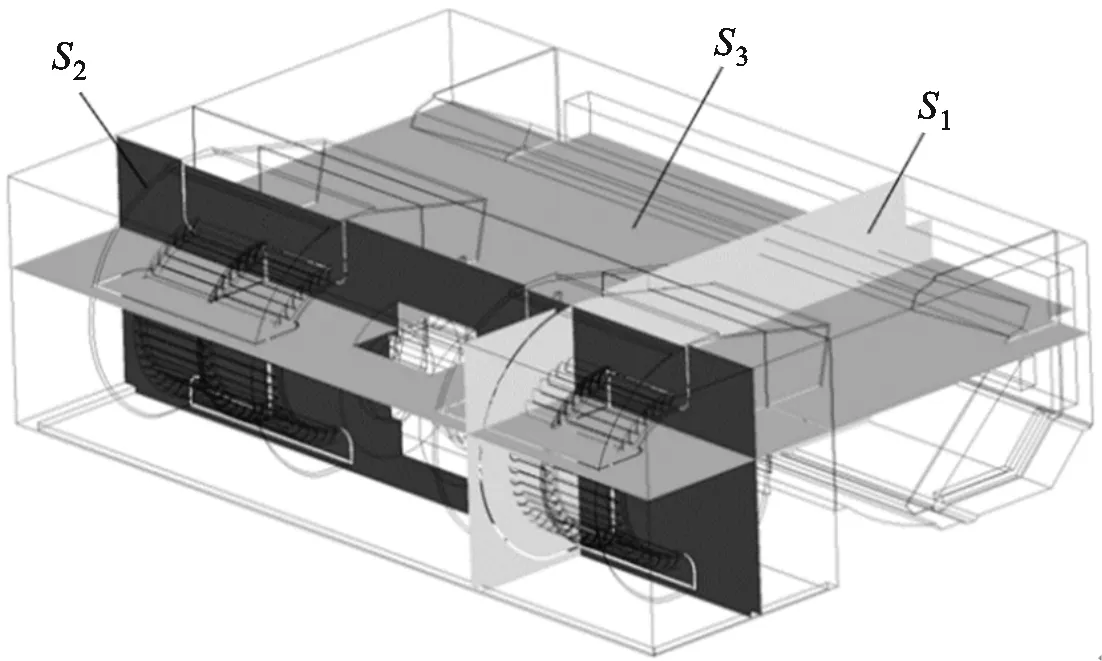
图17 风机盘管整机观测截面位置示意图

图18为原型方案与A1方案叶轮的50%叶高截面速度流线。由图18可以看出,叶轮流道内的分离现象主要发生在叶片吸力面侧,并从蜗舌区域向下游延伸。采用吸力面仿鱼形叶片的叶轮显著减小了此处的流动分离,通过重新优化叶片中弧线和叶片型线,使得叶片的进出口角更加贴合气流的流动,降低了气流与叶片之间的冲击作用。吸力面的仿鱼形轮廓在叶片前缘产生强烈的吸力作用,加速叶轮流道内气体的流动,流道内的旋涡明显小于原型叶轮。对于单风机和整机而言,吸力面仿鱼形叶片都有明显的性能提升效果,表明叶轮的优化能够显著提升多翼离心风机的抗静压能力,有效拓宽风机的工作范围。

(a)原型A0方案 (b)优化A1方案

图19为优化A1和A2方案的单风机和整机S1截面速度云图,通过对比单风机和整机的流动状态可以清晰地看到将单风机优化结构应用到整机上的前后变化。对比图19(a)、图19(c),发现采用偏流蜗壳型线优化之后Ⅰ区的低速叶道明显减小,这主要得益于吸力面仿鱼形叶片与偏流蜗壳型线良好的匹配效果,使叶轮流道内的流动更加顺畅。原型蜗壳的Ⅱ区进行了切割处理,导致蜗壳截面的速度分布不均匀,并影响了上游叶轮流道内的流动。A2方案采用的偏流蜗壳型线能够在尺寸限定条件下有效改善蜗壳内的流动状态,避免了蜗壳内分离造成的流动损失,蜗壳流通截面内的速度分布更加均匀。

将单风机应用到整机上都出现了气动性能的明显下降。对比图19(a)、图19(b),在整机状况下,Ⅰ区的低速叶道明显增加,流动分离严重,气动性能明显不如单风机。对比图19(c)、图19(d),优化之后的方案同样有此特性,在靠近蜗舌附近的叶轮流道内产生大量低速叶道,优化效果甚至不如A1方案,且叶轮进出口逆流现象有所增加。这主要是由于运行工况发生了变化,风机周围增加了整机箱体和换热器,流动阻力增加,使风机工况点都向小流量点偏移。对比图19(b)、图19(d),在整机状态下,A2方案的Ⅲ区蜗壳出口部位与A1方案相比存在明显的低速区,蜗壳有效出口面积减小。这表明蜗壳型线的优化影响了风机的抗静压能力,在低静压工况下有不错的性能提升,在高静压工况下反而会导致流动受阻,性能降低,这也是ε2=0的原因。A2方案虽然对整机没有提升效果,但是能够在保持整机风量不变的状态下有效提升单风机的风量,因此在下一步优化过程中保留此优化步骤。

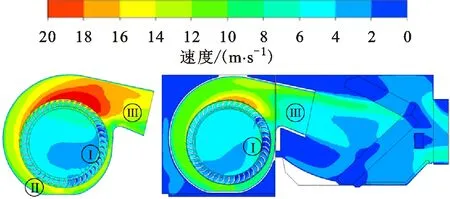
(a)优化A1方案单风机 (b)优化A1方案整机

图20为优化A2和A3方案的单风机和整机S2截面速度云图,该风机为双吸式多翼离心风机,中盘两侧的流场基本呈对称分布。对比图20(a)、图20(c)可以看出,A3方案采用了外凸集流器,使Ⅳ区附近的速度分布更加均匀,有效降低了叶轮前盘与集流器间隙处的逆压梯度,减小了泄漏气流,单风机的性能得以有效提升。对比图20(a)～图20(d)可以看出,单风机与整机状态下蜗壳内部的流动状况有很大的区别。单风机的Ⅴ区流场均匀对称分布,比较符合蜗壳内气体分布规律,但是整机状态下Ⅴ区流场分布较为混乱,这主要是因为整机进气结构复杂,气流进入蜗壳需进行90°的偏转,产生较大的流动和分离损失,导致中盘两侧的流场呈现非对称分布。对比图19(b)、图20(d),外凸集流器由于存在凸起,导致整机的进气状态更加复杂,反而不利于风机的进气,因此在下一步的优化过程中放弃此优化步骤。

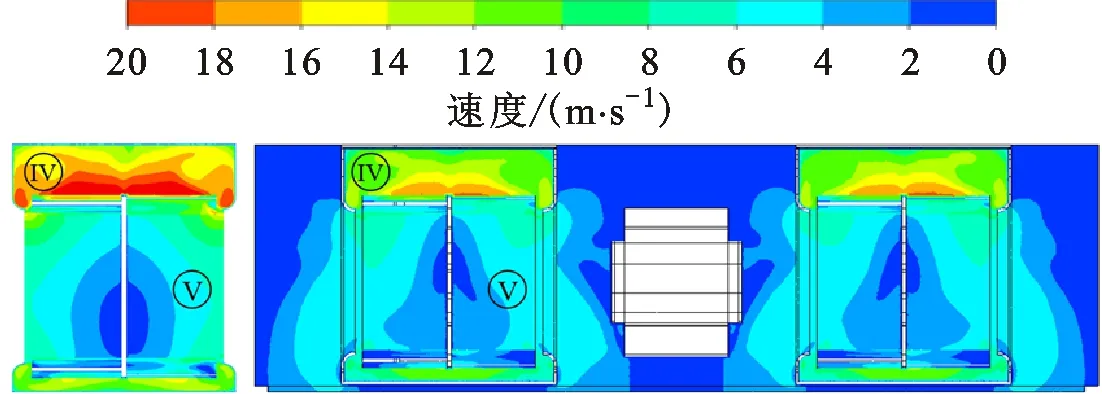
(a)优化A2方案单风机 (b)优化A2方案整机

图21为优化A2和A4方案的蜗壳表面湍动能分布云图。A4方案将蜗舌的形式由原来的深舌改为浅舌,原蜗舌处的强湍动能区域得到有效抑制,湍流脉动所导致的蜗舌表面的压力脉动明显减小。A4方案蜗舌附近及其下游蜗壳表面的湍动能分布更加均匀,使得风机内部的复杂流动状态得到改善,有效降低了蜗壳通流截面之间的二次流和气流冲击作用,但是蜗舌形式改变带来的性能提升并没有充分体现在整机上。

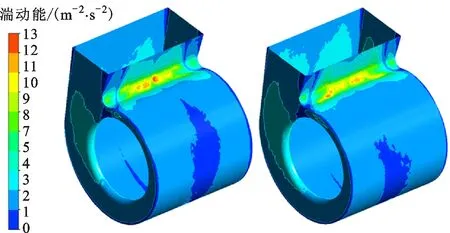
(a)优化A2方案 (b)优化A4方案

图22为蜗壳出口截面总压分布,A4方案由于蜗舌形式的改变出口面积有所增加,出口气流流速降低,导致出口总压分布不均。蜗壳出口下侧负压区明显大于A2方案,导致出口回流。应用于整机之后,由于蜗壳出口静压的增加,进一步加剧了回流,使得优化方案在整机上并不能带来明显的性能提升。

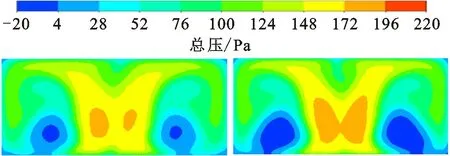
(a)优化A2方案 (b)优化A4方案

图23为原型方案和A4方案的整机S3截面速度云图,该截面云图能够大致表现出风机盘管整机内部的流动状态。

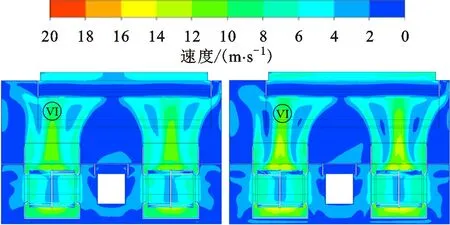
(a)原型A0方案 (b)优化A4方案

Ⅵ区为风机盘管内部主流区,气流从蜗壳出口流出,流经换热器。对比图23(a)、图23(b),优化整机相比于原型整机Ⅵ区高速气流明显增加,且在Ⅵ区主流区域两侧形成了小范围的低速区。换热器两侧存在一个间隙空间,该空间会形成两个局部的旋涡,降低整机的流动效率。A4方案的整机出口气流更加均匀,原型整机出口中间部位存在一个延伸的低速区,影响整机出口气流的均匀性。