积分的计算及其应用探讨
2022-07-19阿布力米提孜克力亚库福立
◎吕 军 阿布力米提·孜克力亚 库福立
(新疆农业大学数理学院,新疆 乌鲁木齐 830052)
一、引 言
《高等数学(上、下)》研究的主要问题就是函数的基本形态和相关性质,高等数学上册主要介绍的是一元函数的微分学和积分学,而下册则主要介绍了多元(二元)函数的微分学和积分学两方面内容,而(不)定积分作为函数积分问题的开端,如何能够让学生更加深刻地理解及深入的掌握就显得至关重要,特别是对于理工类高校的学生,(不)定积分在其自身专业课的学习中应用较广,本文旨在学生掌握基本积分的计算方法的基础上,提供若干的技巧和方法,并给出相关的应用,从而提高学生的学习能力和利用所学解决实际问题的能力
二、积分计算方法与技巧
(一)凑微分法
1 设()具有原函数,=()可导,则有换元公式:


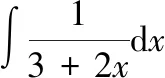

令=3+2,则有


(二)第二类换元法


注:第二类换元法主要分为以下四类:
1三角代换
当被积函数中含有



2倒代换

3根式代换




4指数代换




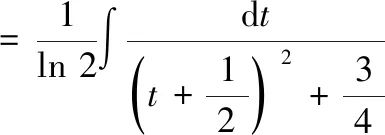



(三)分部积分法




积分类型u,dv的选择1∫Pn(x)ekxdxu=Pn(x),dv=ekxdx2∫Pn(x)sin (ax+b)dxu=Pn(x),dv=sin (ax+b)dx3∫Pn(x)cos (ax+b)dxu=Pn(x),dv=cos (ax+b)dx4∫Pn(x)ln xdxu=ln x,dv=Pn(x)dx5∫Pn(x)arcsin(ax+b)dxu=arcsin (ax+b),dv=Pn(x)dx6∫Pn(x)arccos (ax+b)dxu=arccos (ax+b),dv=Pn(x)dx7∫Pn(x)arctan(ax+b)dxu=arctan(ax+b),dv=Pn(x)dx8∫ekxsin (ax+b)dxu,dv 可任选其一9∫ekxcos (ax+b)dxu,dv 可任选其一
(四)添项法
添项法是在计算不定积分时常用的一种方法,一般是根据被积函数的特点进行加减添项或是乘除添项

通过观察∵(e)′=e,对被积函数分子分母同时乘e,则有


=-ln(e+1)+
(五)二次循环法


直接连续利用两次分部积分公式




移项、化简后可得

(六)待定系数法
待定系数法是一种重要的数学方法,通过引入一些待定的参数,对不定积分进行求导,进而比较同类项的系数,从而转化为求解相应方程组的一种求解方法,待定系数法的好处在于可将比较复杂的不定积分求解简易化,降低求解不定积分的难度
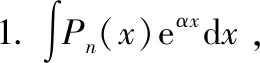



(七)利用留数定理






其中,(=1,2,…,)为包含在||=1内的()的奇点
(八)变量代换法
当遇到被积函数是无理函数时,我们常常会利用变量代换法,其代换的主要目的就是能去掉被积函数中的根号,从而达到简化计算的目的,具体有以下几种类型,见下表:

被积函数形式相应的变量代换1∫Rx,n1ax+bcx+d,n2ax+bcx+d,…(nkax+bcx+d)dxtN=ax+bcx+d,N=lcm(n1,n2,…,nk)2∫R(a+x,x+b)dxa+x=b-asht3∫R(a-x,b-x)dxa-x=b-atan t4∫R(x-a,b-x)dxx-a=b-asin t5∫R(x-a,x-b)dxx-a=b-asec t




(九)部分分式展开法
我们知道任何一个多项式可以分解成若干个一次因式和二次因式的乘积因此,任何一个有理真函数必定可以表示成若干个部分分式之和
如果()是的实系数有理真分式,即下式中的<,则()一定可以写成:

值得注意的是,要用部分分式展开方法,首先要求解分母()=0的根,称为()的极点

首先将被积函数展开成部分分式的形式,令:

则由待定系数法可知:=2,=-3,=1

=2ln||-3ln|+1|+ln|+2|+
三、定积分的应用
积分的几何应用主要有以下几种:(1)利用积分可以求平面图形的面积(2)利用积分可以求空间立体的体积(3)利用积分可以求解曲线的弧长(4)利用积分可以求旋转曲面的面积具体如下:
(一)平面图形的面积
(1)若平面图形是由上、下两条曲线=(),=()(()≤())与直线=,=(<)所围成的,则的面积为:

(2)若平面图形是由左、右两条曲线=(),=()(()≤())与直线=,=(<)所围成的,则的面积为:

(3)若平面图形是由极坐标下的两条曲线=(),=()(()≤())与射线=,=(<)所围成的,则的面积为:





(二)空间立体的体积
(1)设立体Ω介于两个平面=,=(<)之间,∀∈[,],过点作平面垂直于轴,则该平面与立体Ω的截面为可求的连续函数(),则立体Ω的体积为

(2)平面图形:{(,)|()≤≤(),≤≤}绕轴旋转一周所得的旋转体的体积为

(3)平面图形:{(,)|()≤≤(),<<,≥0}绕轴旋转一周所得的旋转体的体积为

9一平面经过半径为的圆柱体的底圆中心并与底面交成角为,计算这个平面截圆柱所得立体的体积
如图所示

取平面与圆柱体的底面的交线为轴,底面上过圆心且垂直于轴的直线为轴,那么底圆的方程为+=

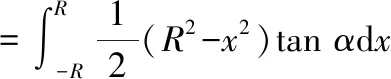

(三)平面曲线的弧长
(1)平面曲线的方程为=() (≤≤),若()连续可导,则曲线的弧长为

(2)平面曲线的参数方程为=(),=() (≤≤),若(),()均连续可导,则曲线的弧长为

(3)平面曲线的极坐标方程为=()(≤≤),若()连续可导,则曲线的弧长为





综上,给出了求解积分的几种常用的方法和技巧,并一一举例,同时也给出了积分的几种常见的几何应用目的是帮助学生更好地去归纳和总结,熟练掌握积分的求解,并能够将其应用到实际生活
