全隐框型玻璃幕墙固有频率影响因素研究

2022-07-18高崇亮曹亚军高勇勇

建筑施工 2022年4期

高崇亮程超王波曹亚军蔡饶高勇勇

中建深圳装饰有限公司广东深圳 518023

随着中国经济的快速发展，城镇化速度逐渐加快，在一些发达城市中，玻璃幕墙的高层建筑成为一道靓丽的风景线，甚至很多拥有玻璃幕墙的建筑成为当地的地标。

传统的建筑也被赋予了新的生命，墙体除了最初的支承作用，也被扩展到采光、隔热、保温、隔声和装饰等作用。玻璃幕墙由于其优异的透光、美观、防风、防雨等特性，加之其自重轻、施工方便、可替换和具有现代风格的特点，逐渐成为办公建筑、商务建筑和超高层建筑的必要部分。

玻璃幕墙作为非承重结构，通过支承架构悬挂在主体结构外侧。但这样的结构并非一直是安全的，以下原因可能导致幕墙玻璃的脱落或是破裂，造成不可预知的后果。

1）早期对玻璃幕墙类建筑没有明确的标准和规范，以及建筑质量参差不齐、监管落实不到位。

2）玻璃幕墙的稳定性会受到风载荷、力载荷、地震等因素的影响。

3）随着时间的推移，胶体材料老化、断裂、腐蚀等各种情况都会出现。

因此，玻璃幕墙支承体系和黏结体系的松动和损伤识别是评价幕墙玻璃安全性能重要指标之一。建立幕墙玻璃固有频率与其边界支承松动损伤之间的关系，就可以通过幕墙玻璃固有频率来间接描述玻璃幕墙支承体系和黏结体系的损伤与老化程度，预测玻璃幕墙的脱落风险程度及抵抗外力的剩余能力，进而评价玻璃幕墙的安全可靠性能。在幕墙玻璃本身性态不发生损伤变化情况下，频率的变化可认为是完全由于其边界支承松动损伤引起的。因此，我们只要通过比较幕墙玻璃固有频率相对大小就可以识别其边界支承松动损伤程度，并依此给玻璃幕墙进行安全等级划分。

1 试验方法

针对安全性能的测试，相关研究人员给出了不同的测试方法。

刘小根等[1]提出了一种利用脉冲激振方法获得幕墙玻璃固有频率来识别玻璃幕墙的松动与损伤程度，试验结果表明四边支承幕墙玻璃试样的边界支承松动会引起其固有频率衰降，从而可根据固有频率的变化来识别玻璃四边支承松动损伤程度。

陈振宇等[2]针对全隐框玻璃幕墙结构胶脱黏长度检测问题，率先提出了基于瞬态脉冲动力响应信号的FFT功率谱脱黏长度检测方法。研究成果显示，此方法对全隐框玻璃幕墙结构胶脱黏长度检测有推广作用。

黄智德[3]以隐框玻璃幕墙和点支承建筑幕墙为研究对象，重点研究了幕墙面板的稳定状态与其动力特征参数之间的关系，并将远程激光测振技术引入幕墙检测，以期实现幕墙面板安全状态的远程、快速、准确的量化评价。

陈玉明等[4]做了基于热图像重建及增强的玻璃幕墙结构胶损伤区域识别方法的研究，主要利用单列位置的数据重建、基于小波变换的图像重构、采用维纳滤波的图像增强和基于损伤区域识别规则的热波定位方法完成玻璃幕墙热图像序列的处理及损伤区域的识别。该试验结果表明：小波变换技术利用自适应阈值系数可有效降低热图像高频分量中噪声成分，保留热图像特征；维纳滤波采用3×3模板进一步平滑图像，确保热图像中大部分重要信息；损伤区域识别率达93.7%。

王永祥等[5]针对玻璃幕墙结构胶老化、失效以及高风压荷载导致的玻璃脱落等安全事故问题，提出了一种基于光纤光栅传感技术对玻璃幕墙边缘动态应力进行检测的方法，构造了玻璃面板边缘应变与结构胶之间的多模态耦合模型，从而预测玻璃幕墙结构安全状况。通过对比分析多模态应变的仿真与试验结果数据可以得到：准分布光纤光栅能够给出结构胶的失效位置，提前对玻璃幕墙结构胶的健康状况进行安全性能评估与反馈。

2 试验测试仪器及结果

固有频率分析是结构振动固有特性分析之一，且是模态参数中最容易获得的一个参数。

当幕墙玻璃的结构损伤时，其固有振动特性就会发生变化，所以目前利用结构振动的特性参数来检查结构是否完好成为当下的研究热点。

玻璃整体在无约束条件下，正面玻璃固有频率只与边界结构胶的约束状况有关。玻璃自重对约束改变不大，改变激励位置和振动加速度传感器位置来测试固有频率。

2.1 便携式幕墙玻璃板块脱落风险检测仪

幕墙检测评估系统是一款小型的、快速的固有频率检测系统，可对幕墙的振动频谱进行分析，通过人机界面显示结果。同时，将检测信息及时传送到计算机或管理平台，检测仪配有大容量数据存储器，通过USB等标准通信接口与上位机软件建立通信。检测仪应获得玻璃幕墙的振动频谱，并提取固有频率，并且还应包含玻璃、石材幕墙的环境信息，对于系统测试信息的提取、输出、显示和应用等功能的实现。

幕墙检测评估系统硬件由传感器、控制执行器、模数转换电路、模数信号处理电路，以及仪器操作面板和对外通信接口电路组成。中央处理器是检测评估系统的核心，将数字信号进行处理和相关分析提取出所需的测量信息，具体为振动的频谱信息和固有频率。

此外，通过位移、加速度传感器将幕墙板块的振动信息（位移、加速度）转换为系统可以接受和处理的模拟电压信号。通过模拟电路进行模拟信号处理后，形成与振动物理信息对应的高信噪比测量信号，再由中央处理器以测量信息的形式输出测量结果。

2.2 试验测量

常见的玻璃幕墙失效模式有3种：一是玻璃面板失效，二是黏结材料失效，三是幕墙支承结构失效。

本课题首先对黏结材料失效进行模拟，主要包括2种情况：硅酮（聚硅氧烷）结构胶全部老化、硅酮结构胶部分失效。

由于全部硅酮结构胶在相同的大气环境下工作，因此可以假设玻璃幕墙各部位硅酮结构胶的老化程度一样。硅酮结构胶部分失效的情况会造成玻璃面板和支承结构部分脱离。

对于硅酮结构胶全部老化情况，结构胶在使用过程中，黏结性能会逐渐下降。将结构胶放入高温高湿环境进行人工加速老化，并对不同老化时间的结构胶进行加载可获得变形与荷载曲线，如图1所示。因此，在本项目模拟中通过增加硅酮结构胶的弹性模量来模拟其老化，并进一步分析其对玻璃幕墙结构振动特性的影响。

图1 不同老化时间后结构胶荷载-变形曲线

取玻璃面板一边长度a＝600 mm，另外一边长度b从600 mm连续变化至1 000 mm。计算其前4阶振动频率，即m＝n＝1，m＝1、n＝2，m＝2、n＝1，m＝2、n＝2。

图2给出了前4阶模态频率随一边边长的变化曲线。从图中可以看出，随着玻璃面板一边尺寸增大，结构振动频率连续降低。

图2 前4阶模态频率随一边长度变化

图3和图4给出了不同边长以及不同边长变化率下各阶频率的变化率。可以看出，在边长增大2 cm，即改变约3.3%的情况下，频率已发生约5%的改变，当边长进一步增大时，频率改变率随之增加。由此可知，在实际玻璃幕墙检测时，如果不同尺寸的幕墙放在一起比较，较小的尺寸差异会导致较大的频率变化，从而误认为玻璃面板发生疑似脱落，得到错误的检测结论。

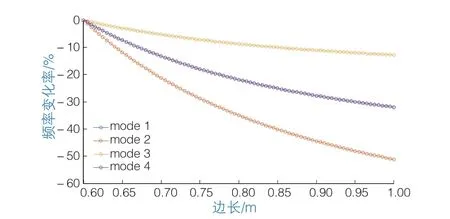
图3 前4阶模态频率变化率与一边长度关系

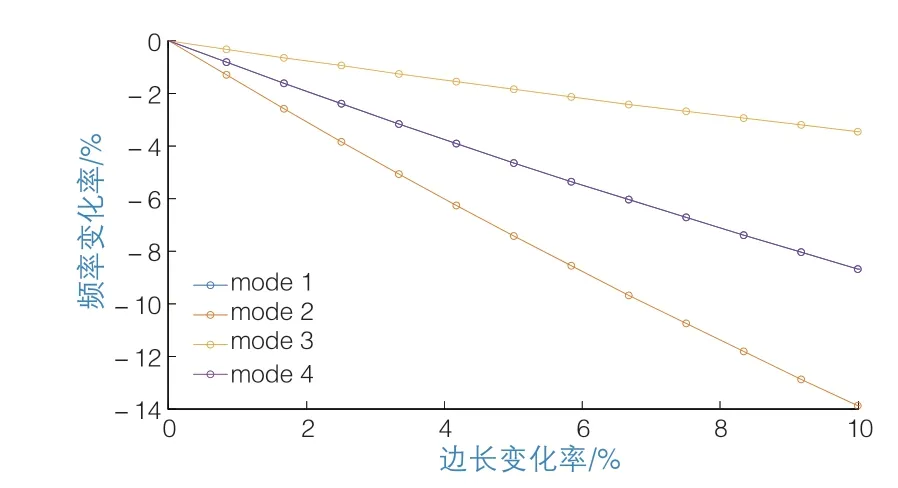
图4 前4阶模态的频率变化率与边长变化率关系

取玻璃面板两边长度均从6 0 0 m m 连续变化至1 000 mm。以第2阶模态为例，由于2个边长均为变量，因此得到频率随边长变化的二维曲面如图5所示。在600 mm×600 mm时自振频率最大，为82.4 Hz，在1 000 mm×1 000 mm时自振频率最小，为29.7 Hz。两边同时变长时，自振频率降低得更快。

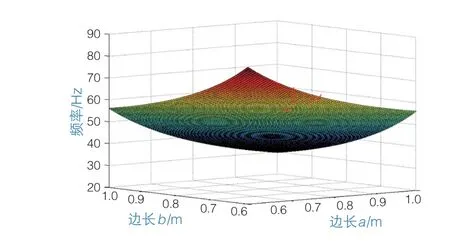
图5 第2阶频率随两边长变化曲面

从试验角度对玻璃振动固有频率随着尺寸的变化进行分析，固定测试板块的宽度为600 mm，改变板块的高度，进行3次测试取平均值作为样品固有频率，数据如表1所示。样品的宽度与固有频率关系如图6所示，固有频率随着高度的增大而减小，符合理论研究结果。

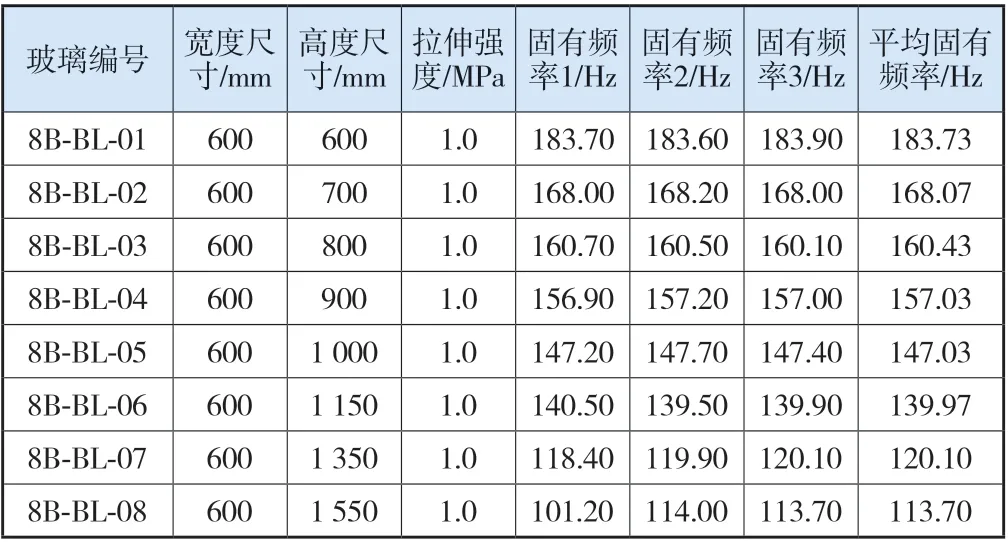
表1 固定宽度玻璃固有频率

图6 不同高度玻璃幕墙固有频率

根据玻璃幕墙板块振型特点，设计测试方案见图7。

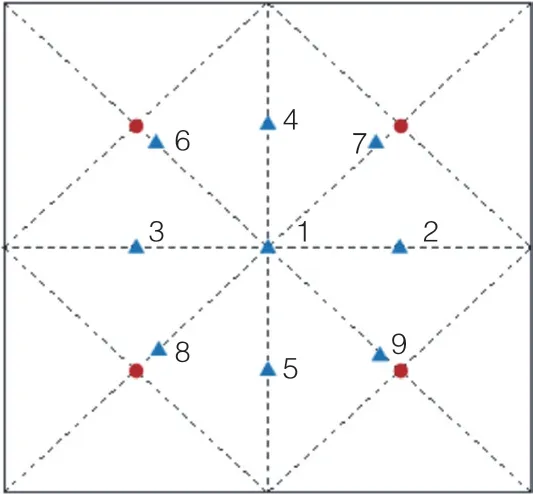
图7 测试方案

图7中红点为传感器位置，共布设4个传感器。蓝色三角形为敲击位置，1为正中心；2和3分别位于左中和右中，两者激励效果等效；4和5分别位于上中和下中，两者激励效果等效；6、7、8和9分别位于对角线上，这4个激励点的激励效果等效。

结果显示：正中心激励时，主要振动频率为175 Hz。2和3点激励时，主要振动频率为148、175 Hz，且148 Hz对应频率幅值更大。4和5点激励时，主要振动频率为175 Hz。6、7、8和9点激励时，主要振动频率为148、175 Hz，且两者幅值基本接近。上述结果可用于指导实际检测时的激励位置。

3 隐框玻璃脱落原因分析

由以上研究内容可知：玻璃脱落意味着作用在玻璃上的外力，主要包括水平方向的风压和竖向的玻璃自重等，超过了结构胶黏结力。借用结构设计中荷载效应与结构抗力需要满足的关系来表示隐框玻璃正常工作所需满足的条件，即：

式中：R——玻璃和结构胶之间的黏结力；

S——作用在玻璃上的外力。

因此，评判玻璃脱落风险需分析黏结力降低的原因和程度。结构胶黏结力属于结构胶与玻璃面板界面之间的相互作用。在玻璃正常受力时，黏结力与外力相平衡，大小与外力一致。我们常说的玻璃脱落其实是外力作用超过了极限黏结力。黏结力是一个分布力，可以考虑为黏结应力（单位面积上的黏结力）与面积的乘积。

结构胶黏结力与2个因素相关：

1）结构胶与玻璃的黏结面积，当结构胶脱落时，黏结面积减小，极限黏结力降低，造成脱落风险升高。

2）结构胶长期使用后材料老化和其他因素导致极限黏结力直接降低，从而造成玻璃脱落风险升高。

4 玻璃振动分析的作用

理论及试验分析表明，玻璃振动频率和振型由以下4个因素决定：

1）结构胶相关的边界条件1：结构胶的黏结面积。

2）结构胶相关的边界条件2：结构胶本身具备的弹性模量。

3）玻璃的几何尺寸，包括边长和厚度。

4）玻璃的物理参数，包括密度、弹性模量和泊松比。

上述因素中，通过大量的振动测试与数据分析，可以得到振动频率与结构胶黏结面积（亦可表示为结构胶脱落长度）之间的关系，从而在新的测试中可以通过振动频率判断结构胶脱落情况和玻璃脱落风险。

而上述因素中的2）、3）和4）则是识别1）过程中的干扰因素。因此，需要研究结构胶老化导致其弹性模量增大对玻璃振动频率的影响、温度变化导致结构胶弹性模量变化对玻璃振动频率的影响以及玻璃尺寸变化对玻璃振动频率的影响。当排除上述因素影响后，可更精确地识别判断脱胶情况。

需要指出的是，上文中提及的黏结力是界面中的静力，极限黏结力的大小不影响玻璃振动模态。黏结力对玻璃振动模态的影响只体现在有和无上：黏结力存在，结构胶就能起到约束的作用；黏结力不存在，边界条件改变，振动模态受到影响。

同时，对于结构胶和玻璃之间的黏结力目前尚未见到相关文献和研究数据。根据推测，结构胶和玻璃之间的极限黏结应力（或称黏结强度）与玻璃表面清洁度、施工质量、使用年限（老化程度）等有关。因此，可通过试验研究结构胶黏结力与上述因素之间的关系，然后在实际检测中，利用该关系，对黏结力进行估计。估计得到的黏结力与玻璃脱落风险直接相关。