基于离散单元法的单螺杆挤出机固体粒子输送特性分析

李良，朱向哲，吴婷婷

基于离散单元法的单螺杆挤出机固体粒子输送特性分析

李良1，朱向哲1，吴婷婷2

（1.辽宁石油化工大学 机械工程学院，辽宁 抚顺 113001； 2.山东康源安全技术咨询有限公司，山东 济南 250014）

基于离散单元法，利用建模软件Solidworks、离散单元模拟软件EDEM，对单螺杆挤出机固体颗粒输送运动进行模拟。研究内容包括物料参数如颗粒的形状、大小，螺杆转速，结构参数如螺棱数量、螺棱倾角对固体输送量的影响，以及机筒内部颗粒的运动和填充情况。结果表明，单一螺杆⁃机筒模型存在最佳颗粒粒径、最佳颗粒形状；颗粒直径越小，填充效果越好；螺棱倾角为105°时颗粒输送量最大。

离散单元法； 单螺杆； 颗粒输送

螺杆挤出成型是聚合物工业生产中最重要的成型方法之一[1]。螺杆挤出成型技术随着时代的发展已经足够完善，根据其对物料的作用，工作过程可分为三个阶段：固体输送阶段、熔融阶段和熔体输送阶段[2]。其中，固体输送阶段的研究基于固体摩擦理论、黏性牵附理论、能量平衡理论[3]。通过固体输送阶段的研究，可以优化螺杆和机筒结构，选择适宜的颗粒，提高输送量和稳定性。固体摩擦理论、黏性牵附理论、能量平衡理论都建立在固体塞假设[4]之上，然而固体输送过程中颗粒间的相对滑动与其不符，故需要更贴合实际的理论基础，即离散单元法。

离散单元法不是传统的固体输送理论，而是一种新的数值方法[5]，拥有相近于有限元法和边界元法的物理意义和数学概念，最初应用于岩石力学。在离散单元法中，建立单个颗粒模型并以此作为分析的最小单元，认为整体来自一系列最小单元的离散运动，在每个单元的接触和分离过程中，使个体具有单独计算的可能，为颗粒力学提供了一个新的解题方法。

1 离散单元理论模型分析

在模拟研究过程中，鉴于高分子固体材料的物理性质，将其视为刚性球形粒子；根据两个球形粒子接触时产生的作用力，以弹簧表示球形粒子接触时发生的弹性碰撞，以黏壶表示球形粒子接触时产生的阻尼，以此建立球形粒子的接触模型，结果如图1所示。图中，i、j表示球形粒子。

图 1　球形粒子的接触模型

Herze理论[6]不考虑颗粒间的黏连作用，因而不适用于本文模型的计算。JKR理论认为黏连作用只发生在两个球的接触面，且认为其接触面是圆形的，因此选择JKR理论对本文模型进行数值研究[7]。

式中，为颗粒外载荷法向分量，N；*为两个颗粒重叠部分半径，m。

接触面半径的表达式为：

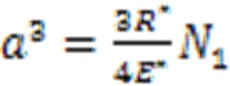
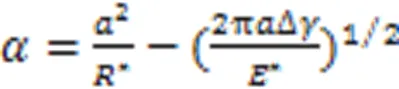
当0时，计算可得：

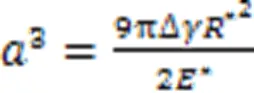
在切向力计算中，当两个颗粒处于分离阶段时，没有滑移，同时切向力改变两个颗粒的接触状态，其切向力增量与切向位移增量的关系式为：

此时，接触面半径的表达式为：

将法向力和切向力代入牛顿第二定律中进行计算，可以得出颗粒i、j的运动参数，进而算得粒子群的运动参数。

使用EDEM软件中的模型创建、仿真计算和数据分析三个模块，对离散单元进行分析[8⁃9]。首先，使用建模软件Solidworks建立螺杆的物理模型，螺杆和机筒的几何和材料参数见表1[10]；其次，在网格划分后选择粒子接触模型，即球形粒子黏弹碰撞模型[11]。基于颗粒碰撞模型理论的螺杆模拟模型示意图如图2所示。颗粒的材料为 LDPE，其颗粒直径为3 mm，螺杆的转速为83 r/min，仿真时间为37 s。料斗应保证颗粒的供应量，避免因颗粒不足而导致输送量和填充率的减小。颗粒的性能参数见表2。

表 1　螺杆和机筒的几何和材料参数

图2　基于颗粒碰撞模型理论的螺杆模拟模型示意图

表2　颗粒的性能参数

2 模拟分析

2.1 颗粒在螺槽中的填充及速度分布

设定颗粒直径为3 mm，颗粒形状为球形，螺杆结构为40 mm导程单螺棱螺杆（40 mm单螺棱螺杆，下同），转速为83 r/min，螺棱倾角为90°，考察了颗粒在螺槽内部的填充过程，结果如图3所示。由图3可以看出，=1 s为料斗填充颗粒阶段；当=5 s时，填充尚不完全，颗粒快速地在底部和螺棱推力区域填充；当=10 s时，底部填充几乎完成，开始有颗粒输送；当=15 s和=20 s时，输送段区域填充完成，但出料口区域填充不完全。

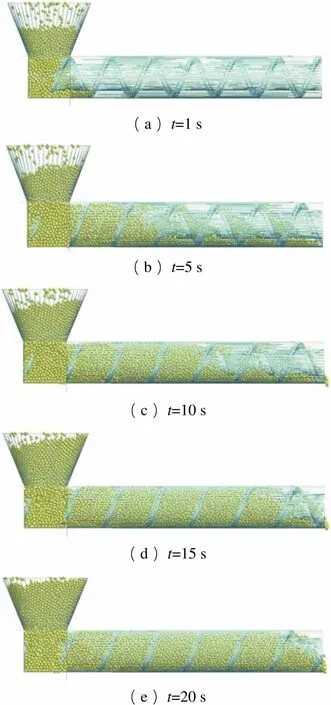
（a）t=1 s （b）t=5 s （c）t=10 s （d）t=15 s （e）t=20 s

借助离散单元法，可选择任意时间点，观察螺槽内粒子的运动速度，这是塞流模型所欠缺的。通过离散单元法研究了螺槽内的粒子速度分布，结果如图4所示。

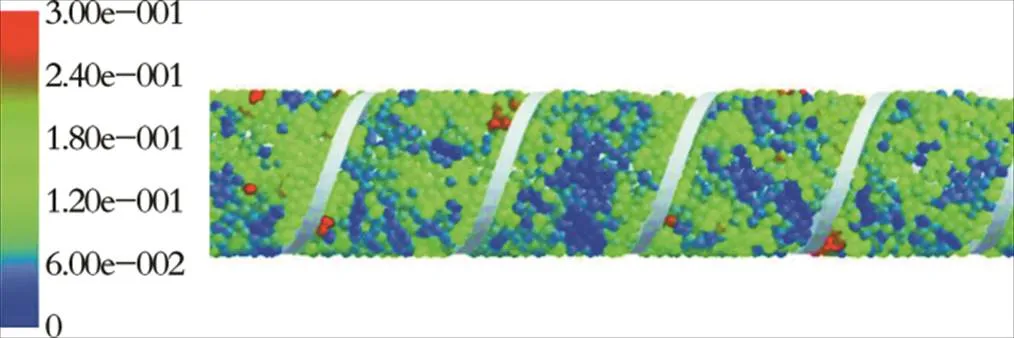
图4　螺槽内的粒子速度分布云图

由图4可以看出，靠近螺棱位置的速度大于中间区域的速度；颗粒从靠近螺棱位置往中间区域过渡时速度降低，这是因为螺棱推力作用的降低；当颗粒从中间区域向螺棱背面位置靠近时，因为螺杆旋转导致螺棱相对位置后移，使颗粒拥有沿螺杆方向运动的空间，运动速度变快。

2.2 材料参数对输送量及填充率的影响

2.2.1颗粒直径 在颗粒形状为球形、螺杆结构为40 mm单螺棱螺杆、转速为83 r/min、螺棱倾角为90°的条件下，考察了颗粒直径对输送量、填充率及填充过程的影响，结果如图5—6所示。

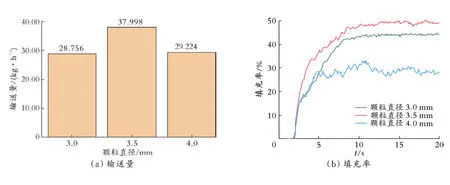
（a）输送量（b）填充率

图6　不同颗粒直径的填充过程

由图5可以看出，颗粒直径对输送量及填充率有显著影响；当颗粒直径为3.5 mm时输送量最大，颗粒直径为4.0 mm时次之，颗粒直径为3.0 mm时输送量最小；当颗粒直径为3.5 mm时填充率最高，颗粒直径为3.0 mm时次之，颗粒直径为4.0 mm时填充率最小。综上，当颗粒直径为3.5 mm时，无论是输送量还是填充率均最优，说明当机筒参数一定时，存在最佳颗粒直径。

由图6可以看出，当颗粒直径为3.0 mm时，填充效果较好，粒子几乎遍布在螺槽中，但是粒子分布不是很均匀；当颗粒直径为3.5 mm时，大多数颗粒呈现一种排列整齐的状态，粒子间空隙小，填充率大；当颗粒直径为4.0 mm时，因为颗粒直径较大，粒子间空隙大，在机筒内分布凌乱，在螺杆输送过程中的填充率低。

2.2.2颗粒形状 选取颗粒体积为14.1 mm³，形状分别为方形、柱形、球形的颗粒，分析了颗粒形状对输送量及填充率的影响。其中，球形颗粒的直径为3.0 mm。为了减少输送末端对填充率的影响，在螺槽的中间截取40 mm的输送段进行研究。三种形状颗粒模型如图7所示。方形颗粒可视为由八个小颗粒叠合而成，以此建立方形颗粒模型（见图7（a）），经计算知其颗粒直径为1.281 0 mm；柱形颗粒可视为两个球形颗粒的组合，以此建立柱形模型（见图7（b）），经计算知其颗粒直径为1.233 5 mm。

在颗粒直径3.0 mm、螺杆结构为40 mm单螺棱螺杆、转速为83 r/min、螺棱倾角为90°的条件下，考察了颗粒形状对填充率的影响，结果如图8所示。

图8　颗粒形状对填充率的影响

由图8可以看出，不同形状颗粒的填充率均从10 s左右开始基本稳定；柱形颗粒的填充率明显高于其他两种形状颗粒的填充率。

颗粒形状对输送量的影响见表3。

表3　颗粒形状对输送量的影响 kg/h

由表3可以看出，方形颗粒和球形颗粒的输送量相近，但方形颗粒的输送量稍低于球形颗粒的输送量；柱形颗粒的输送量明显高于方形颗粒和球形颗粒的输送量。

由此可知，当机筒大小和颗粒直径一定时，柱形颗粒的输送量和填充率优于球形颗粒和方形颗粒，以此可从物料选择方面对输送过程进行优化[12⁃13]。

2.3 螺杆参数对输送量的影响

2.3.1螺杆转速 在颗粒直径为3.0 mm、颗粒形状为球形、螺杆结构为40 mm单螺棱螺杆、螺棱倾角为90°的条件下，考察了螺杆转速对输送量及填充率的影响，结果如图9所示。由图9可以看出，螺杆转速对输送量和填充率的影响显著，螺杆转速越快，输送量越高；螺杆转速越快，填充率达到最高所用时间越短，即前期填充速度更快，但是前期填充完成后，最终填充率差异不明显。

（a）输送量（b）填充率

2.3.2螺杆结构 考察螺杆结构（单螺棱和双螺棱）对输送量和填充率的影响时，为了保证机筒内部空间不变，同时保证螺杆输送段几何结构变化周期不变，添加一条螺棱后，螺杆的导程由40 mm增加到80 mm[14⁃16]。螺杆颗粒填充图如图10所示。在颗粒直径为3.0 mm、颗粒形状为球形、转速为83 r/min、螺棱倾角为90°的条件下，考察了螺杆结构对输送量和填充率的影响，结果如图11所示。

图10　螺杆颗粒填充图

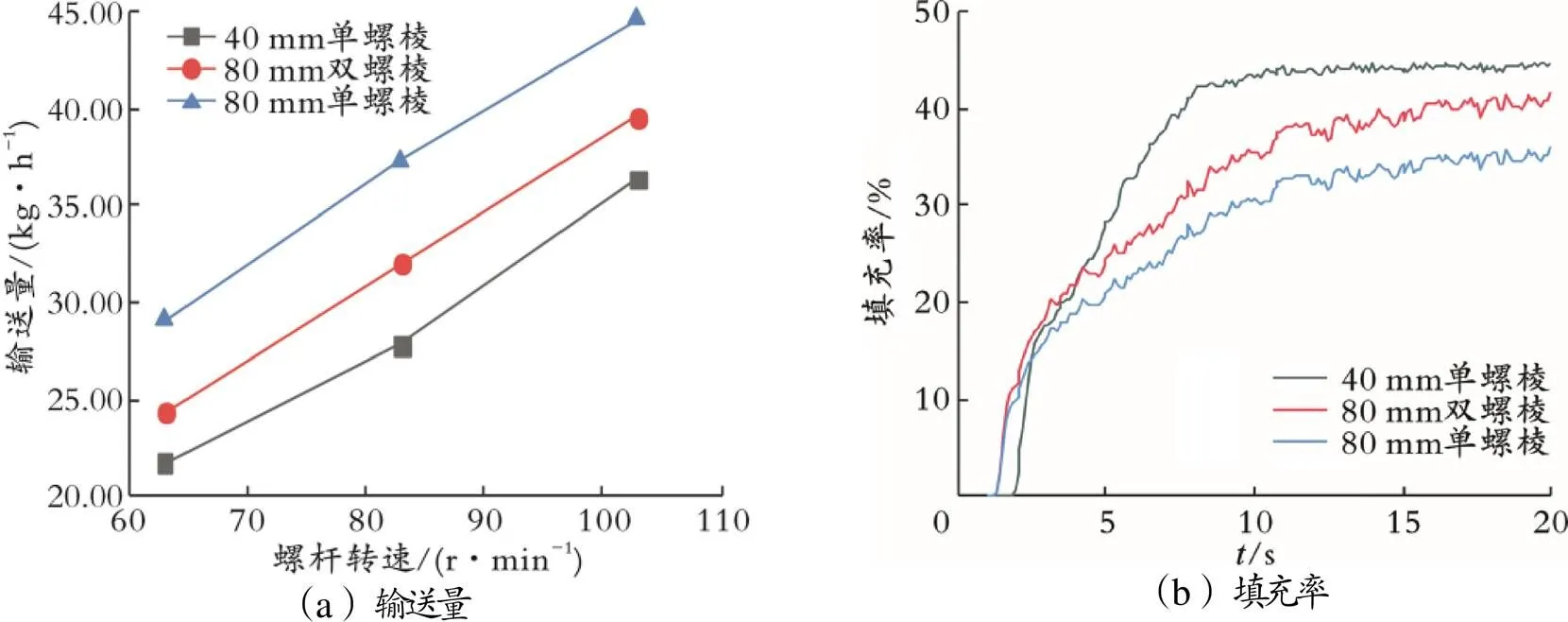
图 11　螺杆结构对输送量和填充率的影响

由图11（a）可以看出，三种结构的输送量变化趋势相近，输送量从大到小的顺序为80 mm单螺棱螺杆、80 mm双螺棱螺杆、40 mm单螺棱螺杆。由图11（b）可以看出，时间小于10 s时，40 mm单螺棱螺杆的填充速度最快，填充率达到最大所用时间最短；时间大于10 s时，40 mm单螺棱螺杆填充率波动幅度最小，即达到最大填充率后稳定性最好；80 mm单螺棱螺杆填充速度最慢，填充稳定性最差。

在颗粒直径为3.0 mm、颗粒形状为球形、结构为40 mm单螺棱螺杆，转速为83 r/min的条件下，考察了螺棱倾角对输送量的影响，结果见图12。

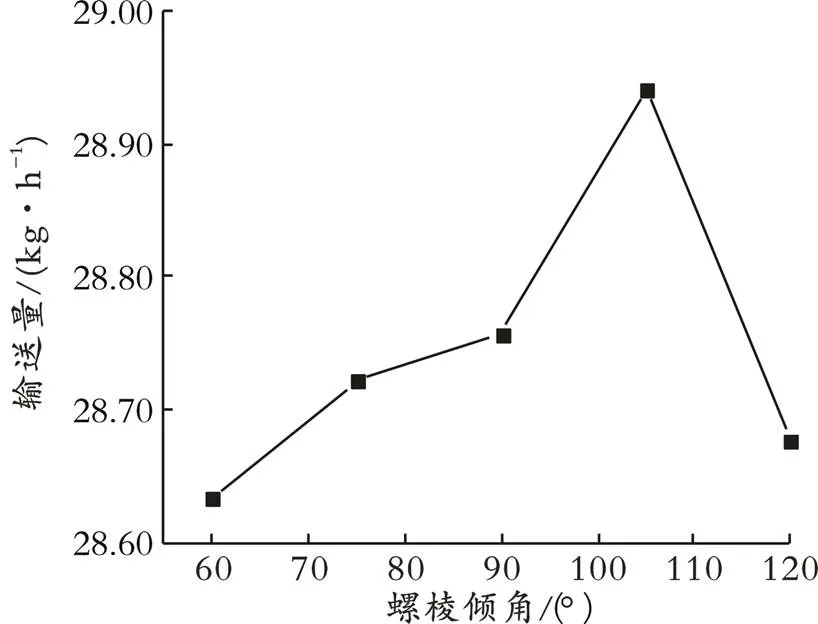
图12　螺棱倾角对输送量的影响

由图12可以看出，螺棱倾角为105°时输送量最大，螺棱倾角为60°、75°、90°、120°时输送量相差不大。

3 结 论

（1）螺棱附近的颗粒速度大于中间区域的颗粒速度。

（2）颗粒输送量及填充率与螺棱数及螺杆导程相关。颗粒输送量从大到小的顺序为80 mm单螺棱螺杆、80 mm双螺棱螺杆、40 mm单螺棱螺杆；40 mm单螺棱螺杆填充速度最快，而且达到最大填充率后稳定性最好，80 mm单螺棱螺杆填充速率最慢，填充稳定性较差，80 mm双螺棱螺杆填充率介于两者之间。

（3）在颗粒直径为3.0 mm、颗粒形状为球形、螺杆为常规单螺杆结构、螺棱倾角为90°时，颗粒输送量与螺杆转速成正比；在同一螺杆结构和转速下，存在一种最佳颗粒直径，使输送量和填充率均达到较好水平；颗粒直径越小，颗粒填充率的变化幅度越小；当颗粒直径一定时，柱形颗粒的输送量和填充率均最优；螺棱倾角为105°时颗粒输送量最大。

［1］ 王建华.单螺杆挤出过程的数值模拟［D］.北京：北京化工大学，2003.

［2］ 袁丁.偏心转子挤出机熔体输运的拉伸形变作用研究［D］.广州：华南理工大学，2018.

［3］ 雷雯.挤出机固体输送段塑性能量耗散的研究［D］.北京：北京化工大学，2016.

［4］ 毛晨.端面螺杆物料输送特性仿真研究及熔体输送阶段参数优化设计［D］.杭州：浙江大学，2019.

［5］ 王泳嘉，邢纪波.离散单元法及其在岩土工程中的应用［M］.沈阳：东北工学院出版社，1991.

［6］ Elsevier.Measurement of the lattice constant of Si⁃Ge heteroepitaxial layers grown on a silicon substrate［J］.Vacuum，1980，30（4⁃5）：202.

［7］ 王亚东，庞学慧，张余升，等.颗粒间粘连力的散体元研究［J］.工具技术，2015，49（2）：16⁃19.

［8］ 王国强，郝万军，王继新.离散单元法及其在 EDEM 上的实践［M］.西安：西北工业大学出版社，2010.

［9］ 胡国明.颗粒系统的离散单元法分析仿真［M］.武汉：武汉理工大学出版社，2010.

［10］ 沈美震.新型偏心双螺杆挤出机混合机理研究［D］.抚顺：辽宁石油化工大学，2020.

［11］ 丁学良，何红，王克俭.单螺杆挤出过程固体粒子输送的离散单元法模拟［J］.塑料，2012，41（5）：92⁃95.

［12］ 高明，陈立，朱向哲，等.转速对密炼机HDPE/PS共混聚合物混合效率的影响［J］.石油化工高等学校学报，2015，28（3）：86⁃90.

［13］ 滕健.偏心双螺杆挤出机混沌混合机理研究［D］.抚顺：辽宁石油化工大学，2020.

［14］ 郑彬，周林非.单螺杆挤出机螺杆的结构设计与优化［J］.塑料工业，2020，48（S1）：93⁃96.

［15］ 谢磊，邹思雨，朱向哲.单螺杆挤出机螺杆组合段流域混合特性［J］.辽宁石油化工大学学报，2021，41（5）：72⁃78.

［16］ 刘睿.螺杆挤出机优化设计现状［J］.塑料科技，2016，44（3）：85⁃88.

Analysis of Solid Particle Transport Characteristics in Single Screw Extrusion Based on Discrete Element Method

Li Liang1， Zhu Xiangzhe1， Wu Tingting2

（1.School of Mechanical Engineering，Liaoning Petrochemical University，Fushun Liaoning 113001，China；2.Shandong Kangyuan Security Technology Consulting Co. Ltd.，Ji'nan Shandong 250014，China）

Based on the discrete element method, this paper uses modeling software Solidworks and discrete element simulation software EDEM to simulate the transport movement of solid particles in a single⁃screw extruder. The research includes the influence of material parameters such as the shape and size of the particles, the screw speed, and structural parameters such as the number of screw edges and the inclination angle of the screw edges on the solid transport capacity, as well as the movement and filling of the particles inside the barrel. The results show that the single screw⁃barrel model has the best particle size and the best particle shape; the smaller the particle size, the better the filling effect; the maximum particle transport capacity is when the spiral angle is 105°.

Discrete element method； Single screw； Particle transport

TQ320.663

A

10.3969/j.issn.1672⁃6952.2022.03.012

1672⁃6952（2022）03⁃0068⁃06

http：//journal.lnpu.edu.cn

2021⁃02⁃04

2021⁃04⁃21

辽宁省教育厅科学研究项目（L2019020）。

李良（1995⁃），男，硕士研究生，从事螺杆挤出机输送特性方面的研究；E⁃mail：2306938845@qq.com。

朱向哲（1974⁃），男，博士，教授，博士生导师，从事计算流体力学和固体力学、机械动力学、流体力学非线性问题等方面的研究；E⁃mail：xzzhu@126.com。

（编辑 宋锦玉）