碳纤维/环氧树脂预浸料固化动力学建模研究

高腾龙,余建虎,许英杰

(1.中国飞行试验研究院,西安 710089;2.西北工业大学 机电学院,西安 710072)

热压罐成型工艺是当前航空航天领域复合材料制件生产成型的重要方法之一,树脂在罐内经历复杂的化学反应和能量交换,从液态到橡胶态最终达到玻璃态完成固化成型[1-2]。树脂在固化过程中会释放大量的热量,使结构件产生一定的温度梯度和固化度梯度,成为复合材料构件产生固化变形的原因之一[3-5]。

国内外众多学者通过DSC试验和DMA试验等对环氧树脂体系进行了广泛的研究。固化动力学研究是研究树脂固化反应的一个重要手段,通过DSC试验可以对树脂或预浸料进行等温固化和动态固化,得出材料的玻璃化转变温度和固化度-温度曲线[6-9]。利用得到的固化速率、温度及固化时间等因素可以预测和控制复合材料成型过程中的固化变形,以提高制件的制造成功率,增加产品质量稳定性,大幅度的提高生产效率。

DSC试验中假设树脂材料的固化度与反应所放出的热量成正比关系,因此可以通过反应的残余热或者反应热来计算固化度的数值。在这一假设下,多种固化动力学方程被研究使用,包括n级反应动力学模型、自催化反应模型和Kamal模型等改进模型[10-12]。但是这些研究都是针对单纯的树脂材料体系进行的,对于复合材料而言,由于纤维材料的加入,使得固化反应产生一定的延缓,因此想要研究复合材料的固化反应模型就需要对预浸料材料进行相应的扫描试验[13-14]。

Shin与Hahn[15]通过DSC试验对AS4/3502材料进行了固化动力学研究,基于自催化模型,通过动态和等温试验确定了模型中的相关参数。Kim等[16]通过动态及等温DSC试验对AS4/3501-6材料进行研究,在文献中采用一种包含两部分的固化反应模型来描述该材料的反应过程。Hayaty等[17]采用动态DSC试验的方法,通过Kissinger、Ozawa和Borchardt-Daniels这3种方法得到模型参数,并对结果进行比较。吴晓青[18]分别采用DSC和DMA试验对TDE-85环氧树脂进行研究,在使用n阶反应动力学方程的基础上,采用极值法、等转化率法和分峰法3种方式确定了模型参数,分析结果可以看到分峰法的结果更为准确。

热压罐成型包含了动态及等温固化过程,因此本文中采用动态试验和等温试验两种方法来研究碳纤维/环氧树脂材料的固化反应。分别采用n级反应动力学模型、自催化反应模型和改进的Kamal模型3种方法进行固化动力学建模,对比发现包含有两子反应的改进Kamal模型能够更好的描述该材料的固化反应过程,并通过等温试验数据验证了模型的准确性。

1 DSC试验

1.1 试验原材料

本文所使用的材料为碳纤维/环氧树脂预浸料体系,单层厚度为0.134 mm,名义树脂含量为35%,单位面积重量为134 g/m2。预浸料储存温度为-18 ℃,并通过真空袋和密封胶带包装。

1.2 试验设备及原理

采用德国NETZSCH公司的DSC 200 F3型号设备进行预浸料的等温及动态固化反应试验,试验设备如图1所示。

图1 DSC差示扫描量热仪

试验前通过铟(纯度为99.99%以上)对DSC设备进行校准,然后再将10～15 mg的预浸料材料放入铝坩埚中进行试验。试验过程中采用氮气作为保护气,通过液氮制冷、炉体加热实现对温度的控制。

试验中,使用热电偶测量样品坩埚及参比坩埚的温度差信号,通过傅里叶传导方程以及热流修正,将原始的温差信号转变成热流差信号,即可以得到热量变化与温度/时间之间的关系曲线。计算得到不同时间、温度下的固化度，即

α=ΔHt/ΔHtotal

(1)

式中:a表示材料在某一时间下的固化度;ΔHt为当前时间反应已经放出的热量;ΔHtotal为材料固化反应的总放热量。

1.3 试验方法

试验共包括动态DSC试验和等温DSC试验两部分。在-50 ℃到350 ℃的温度区间内,分别采用1,3,5,10,15,20 ℃/min这6种升温速率开展动态DSC试验,得到固化反应过程的数据以及试验样品所释放的总热量ΔHtotal。

等温DSC试验则是先通过10 ℃/min的升温速率达到指定温度后保持恒温,在120 ℃,140 ℃,160 ℃,180 ℃,200 ℃这5种温度下分别保持360,240,180,120,120 min。然后再降温至-50 ℃进行动态DSC试验,获得当前材料状态的残余热量、固化度以及玻璃化温度。

2 试验结果

图2为升温速率为20 ℃/min下的动态DSC试验曲线。材料在玻璃化温度附近经历相态的变化导致材料比热有一个突变[19],因此在图2中0 ℃左右,可以看到DSC曲线有明显的吸热现象并呈现出一个下降台阶,我们选取试验曲线上距离两台阶切线相等的点作为玻璃化转变温度Tg。

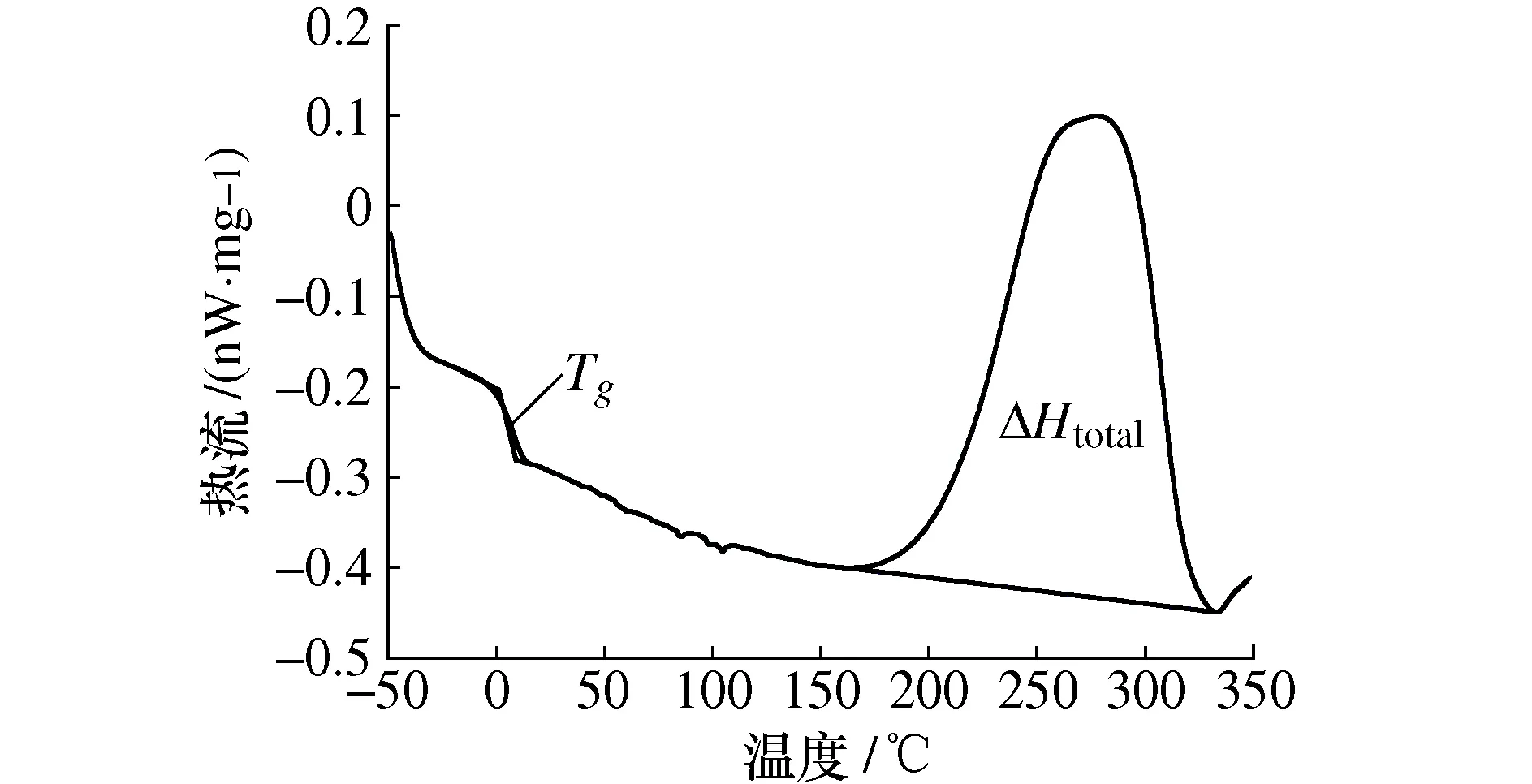
图2 预浸料在20 ℃/min升温速率下DSC试验曲线

图2中的放热峰的总面积ΔHtotal代表固化反应过程的总反应热,其中放热峰面积由图2中所示的切线与DSC曲线构成。

图3为等温试验中温度达到设定温度140 ℃并保持后的部分DSC曲线,图3中起始段的突变是由试验过程中环境温度从动态升温达到恒定温度后,温度速率发生改变引起,这一现象是设备本身造成的。

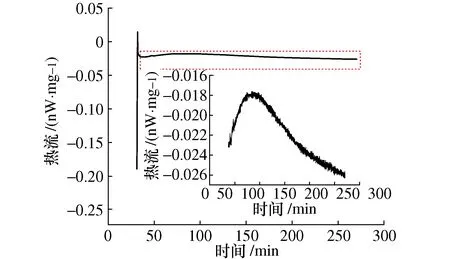
图3 等温DSC试验曲线

选取起始段下降达到极小值点到恒温段结束的区间数据并将其纵坐标放大,得到部分固化反应曲线。该阶段的放热速率在纵坐标区间中占据很小比例,所以在将曲线纵坐标放大后出现较大的波动。在本文中采用动态DSC试验数据用于建立固化动力学模型,而等温试验数据则用于材料的预固化和模型准确度验证[20]。

不同升温速率下动态DSC曲线中的起始温度Ti、放热峰值温度Tp以及终止温度Tf均通过DSC试验测得,其中3个温度分别对应图2放热峰切线起点,峰值以及切线终点。处理试验数据令终止温度Tf时刻所对应的热流作为零值,得到图4所示的预浸料在5种升温速率(1、3、5、10、15以及20 ℃/min)下的动态DSC曲线。

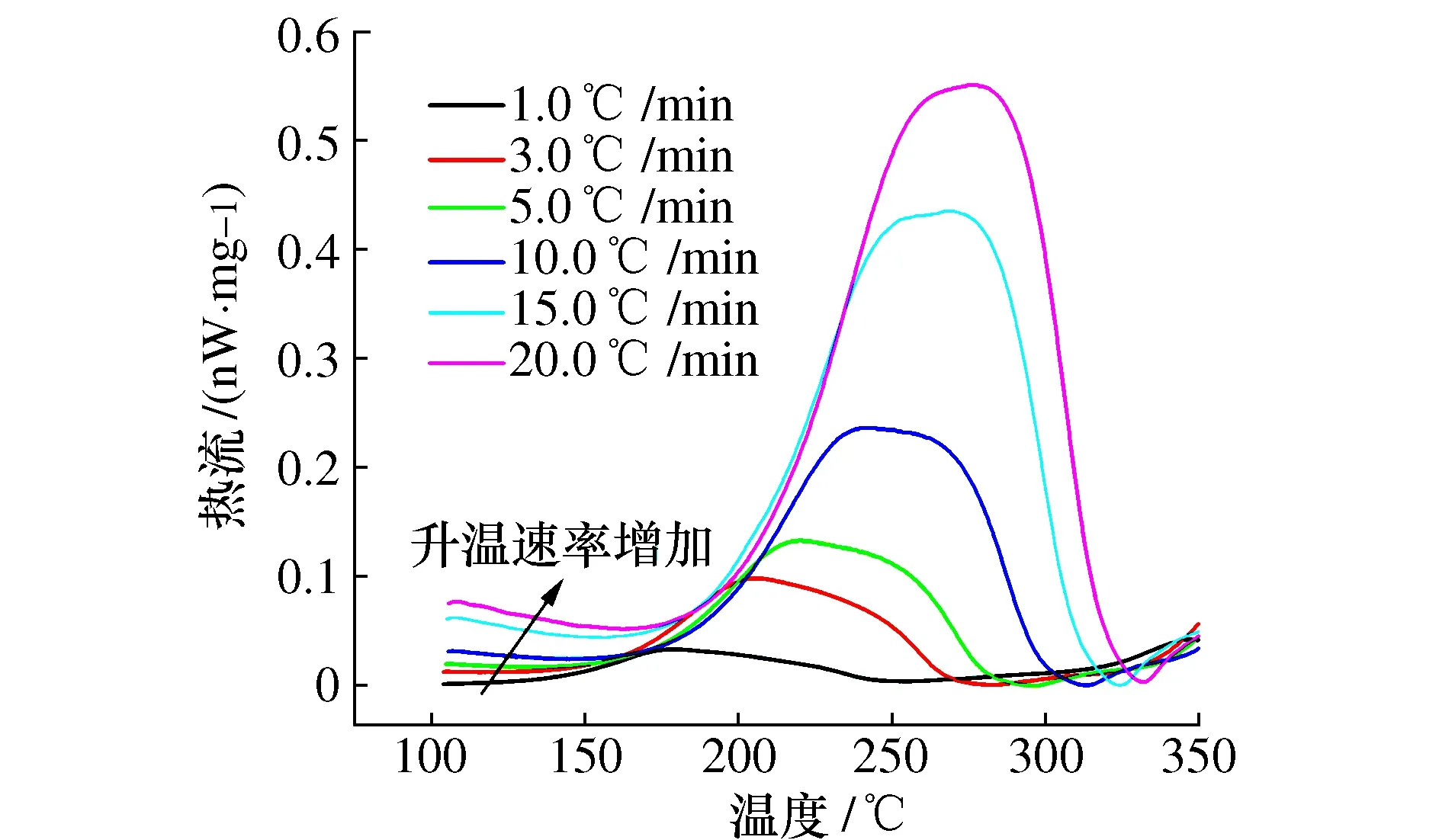
图4 不同升温速率下的DSC试验曲线

随着升温速率的升高,预浸料体系固化反应的放热速率不断增加,同时反应的起始温度、放热峰值温度和终止温度均向高温方向移动,具体数值见表1。

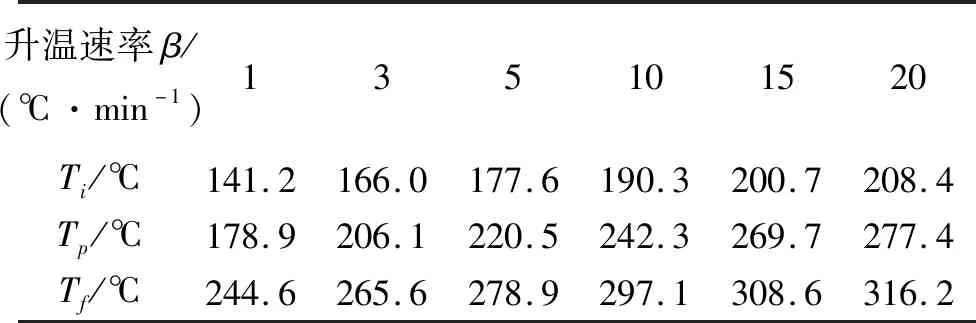
表1 不同升温速率下的特征温度值

不同升温速率下的动态DSC试验总反应热数值如表2所示,本文取其平均值作为该材料体系的总反应热,为120.25 J/g。

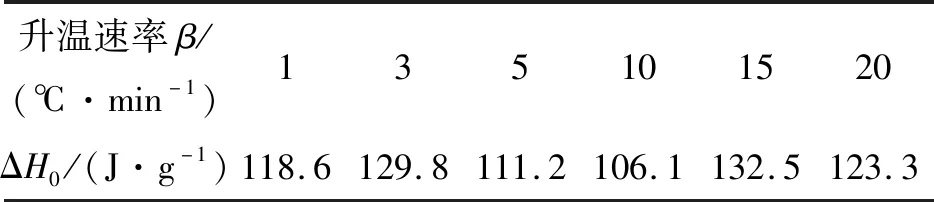
表2 不同升温速率下的总反应热量

玻璃化温度随着固化反应的进行随固化度不断变化,Hesekamp等[21]提出了一种模型用于建立两者之间的关系,如

(2)

式中：Tg(0)表示固化度为0时预浸料的玻璃化转变温度;α为固化度;g1,g2为拟合参数。

表3中汇总了动态及等温DSC试验得到的不同固化度下材料的残余热及玻璃化转变温度,其中经历等温DSC试验得到的预固化材料的固化度为

表3 不同固化度下材料的玻璃化温度和残余热量

(3)

式中ΔHr为固化反应的残余热量。

为减小拟合误差,使用表3中的玻璃化转变温度的绝对温度数值进行非线性拟合,得到拟合参数g1=3.244,g2=7.528。预浸料体系玻璃化转变温度随固化度变化的试验点及拟合数据如图5所示。

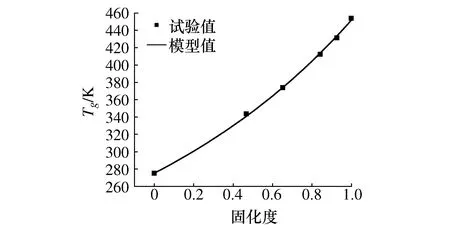
图5 玻璃化温度随固化度变化试验点及拟合曲线

3 固化动力学建模

基于普式动力学方程,利用动态DSC试验数据建立该材料的固化动力学模型,普式动力学方程为[12]

(4)

式中:dα/dt表示固化速率；f(α)为反应机理函数；k(T)为固化反应速率常数,遵循Arrhenius 方程。

k(T)=Aexp(-E/RT)

(5)

式中：A表示频率因子；E代表了反应活化能；普适气体常数R=8.314 5；T是绝对温度。

本文采用Kissinger方程[22-23]来计算模型中的反应活化能和频率因子,具体形式为

(6)

(7)

3.1 n级反应动力学模型

n级反应动力学模型是用于描述固化反应最简单的模型,其表达式为

(8)

式中n为反应级数。

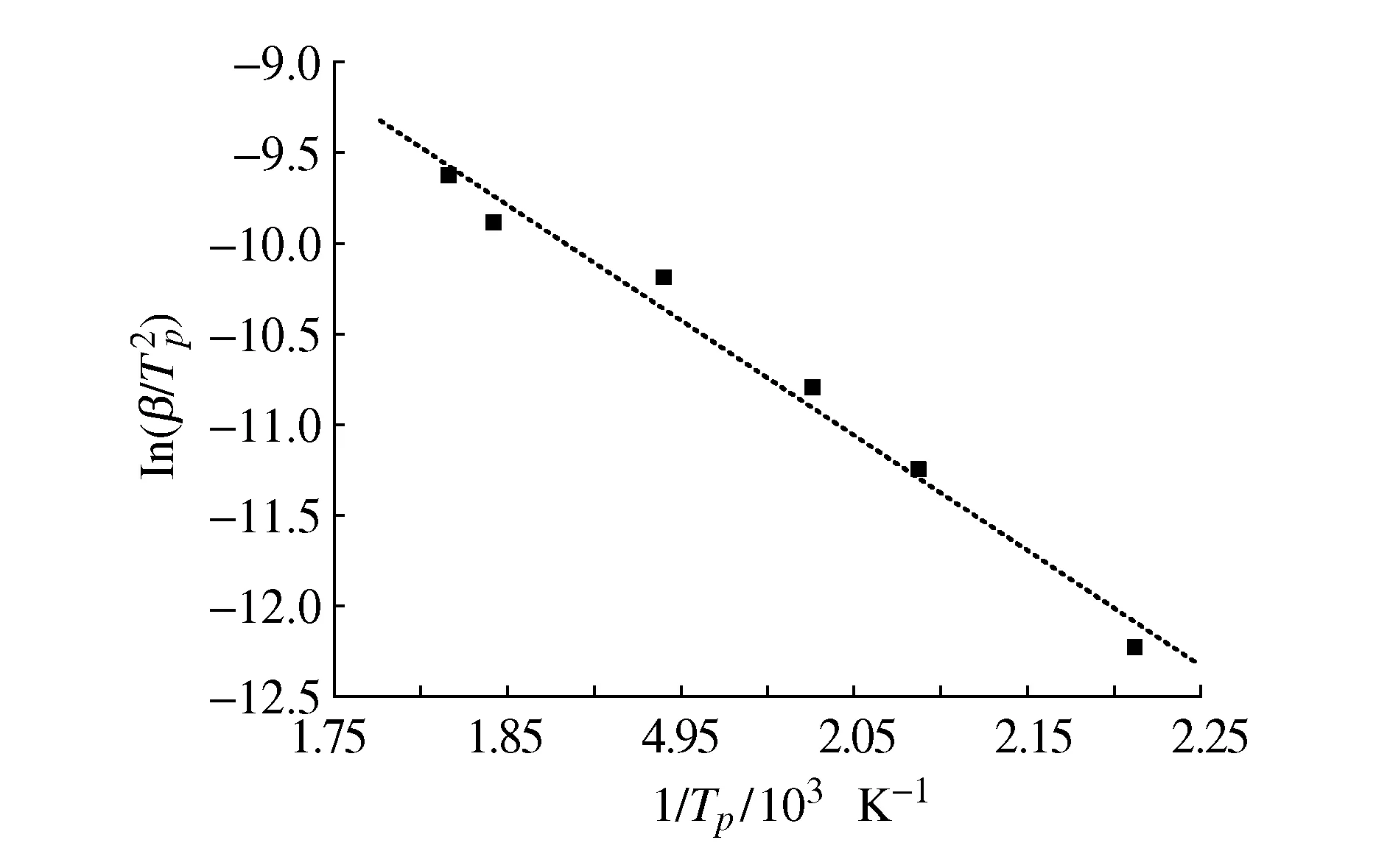
图6 n级反应动力学模型ln(β/2Tp)-1/Tp关系图

对公式(8)进行取对数并移项后得

(9)

取ln(dα/dt)+E/RT和ln(1-α)作图,对数据进行线性拟合得到的直线斜率即为反应级数n。图7显示了两者之间的关系(分别取a=0.1,0.2,0.3,0.4,0.5,0.6,0.7,0.8,0.9,0.93,0.95,0.98为数据点),显然当固化度大于0.8时两者呈线性关系,即主要表现为n级反应;当固化度小于0.8时,呈明显的非线性,因此n级反应模型无法准确描述该材料的固化反应过程。

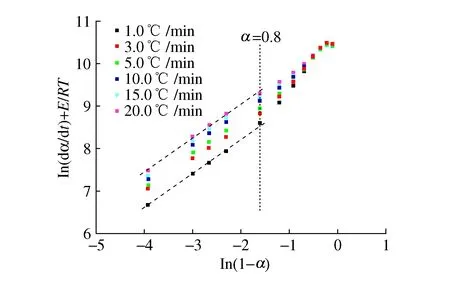
图7 ln(dα/dt)+E/RT和ln(1-α)关系图

为进一步验证n级反应动力学模型对该材料的适用性,通过试验数据单独拟合得到升温速率为10 ℃/min条件下的反应级数数值,取为0.646,并将模型的固化速率/温度曲线、固化速率/固化度曲线与试验数据进行对比,如图8所示。可以看到在反应后期n级动力学模型与试验数值能够很好的吻合,但是在前期有着较大的差距。

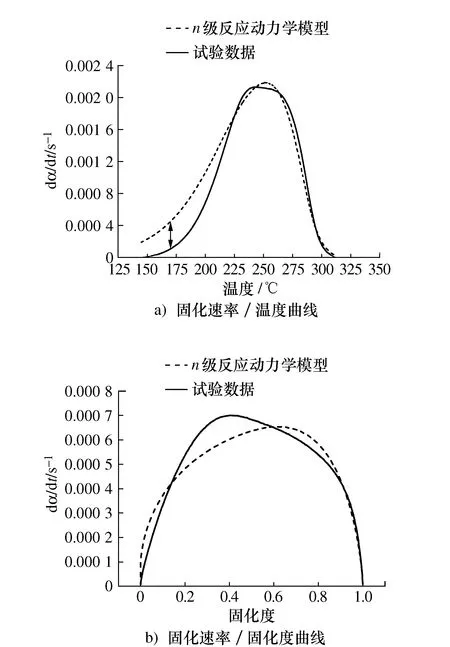
图8 10 ℃/min下n级反应动力学模型与试验数据对比

3.2 自催化模型

自催化模型具有一定的诱导期,固化反应进行一定时间后反应速率才会大幅上升并达到最大值。模型中包含了两个相互独立的反应级数,表示为

(10)

式中m和n均为模型反应级数。

图9中的固化度曲线呈现出明显的“S”形,并随着升温速率的升高向高温方向移动,具有较为明显的自催化反应特征[24]。

图9 动态DSC试验固化度随温度变化曲线

模型中的反应活化能仍然由Kissinger方程求得,取E=52.8 kJ/mol。对模型中的其他参数进行非线性拟合[25],结果见表4。指前因子A随着升温速率的增加不断增加,反应级数n则随升温速率的增加而减小。相比之下,反应级数m则变化较小,无明显趋势。

表4 自催化模型动力学参数拟合结果

图10显示了不同升温速率下自催化模型固化反应速率曲线与试验结果的对比。可以看出模型与试验数据在固化反应前期能够较好的吻合,但是在反应中期和后期的预测存在较大误差。

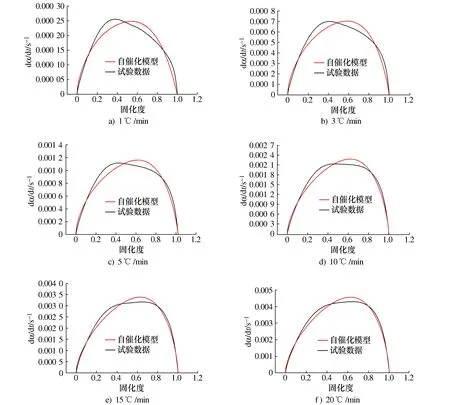
图10 自催化模型拟合曲线与试验数据对比

分析图10中的试验数据发现,结果中除有一个明显的峰值外,还存在着一个较平缓的台阶。升温速率在1～10 ℃/min时,这一台阶出现在峰值的右边,升温速率大于10 ℃/min之后,台阶则出现在了峰值的左边。因此,预测该预浸料体系在固化过程中存在两个子反应,前期的反应符合自催化模型,后期反应符合n级动力学模型[24]。

3.3 改进的Kamal模型

常见的Kamal模型的形式为

A2exp(-E2/RT)αm(1-α)n

(11)

该模型是自催化模型及n级反应模型的组合,在组合的同时共用了反应级数n。为了能够更加灵活、准确的描述该预浸料体系的固化动力学模型,我们将其形式进行适当改进,即

A2exp(-E2/RT)(1-α)n2

(12)

该模型包含了3个相互独立的反应级数,是自催化模型和n级反应模型的叠加。

图11显示了升温速率β=10 ℃/min时的反应速率与温度的关系,可以看到曲线在240 ℃附近达到极大值,我们取其作为前期反应1的峰值。在此之后反应速率并没有迅速的下降,而是出现了较为平稳的台阶,我们取台阶之后开始较快下降的转折点作为后期反应2的峰值,代表另一个化学反应的最大速率位置。不同升温速率下对试验数据进行分峰处理的结果见表5。

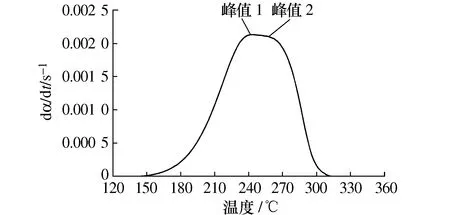
图11 升温速率为10 ℃/min时的分峰结果

表5 不同升温速率下的峰值温度

将固化反应速率的最大值定义为1,对整个反应速率/固化度曲线进行成比例的变化,显示如图12所示。可以明显的看到,随着升温速率的增加,反应2的速率峰值逐渐超过反应1,表明反应2的反应程度越来越激烈。

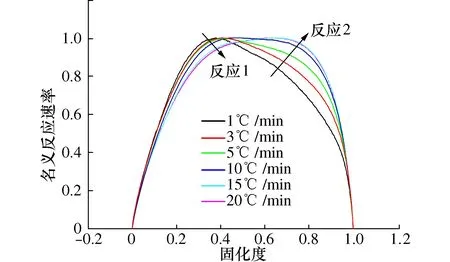
图12 固化度与反应速率的关系

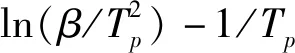
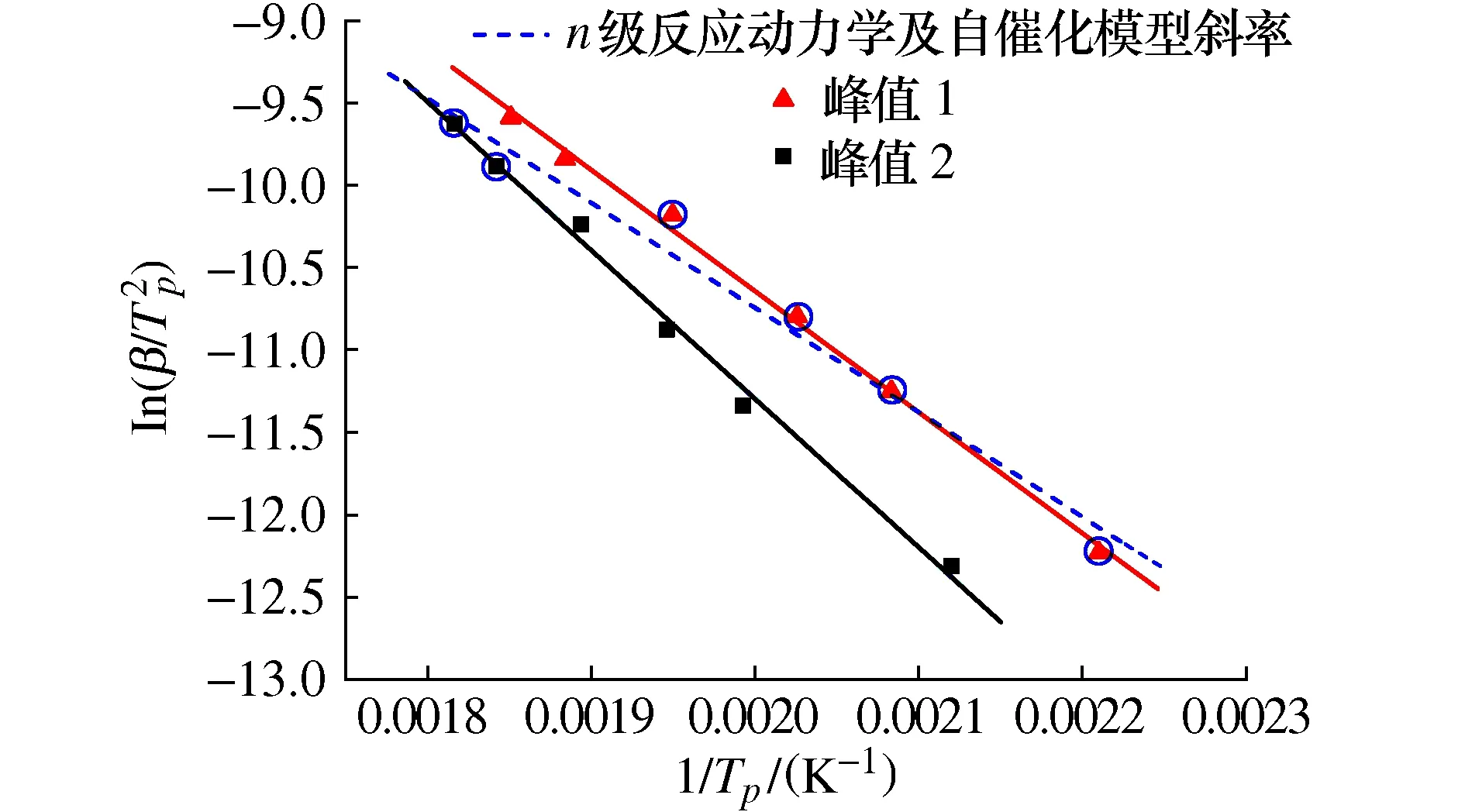
图13 Kamal模型中两子反应的关系图

通过非线性拟合计算得到改进Kamal模型中的参数,其结果如表6所示。

表6 改进的Kamal模型参数拟合结果

图14为改进Kamal模型的固化反应曲线和试验数据的对比结果,可以发现两者能够很好的吻合,能够较准确的描述该预浸料体系的固化反应过程。

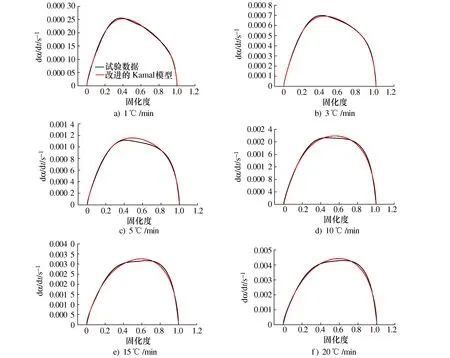
图14 改进的Kamal模型拟合曲线与试验数据对比

以升温速率为3 ℃/min的动态DSC试验为例,对3种模型拟合结果和试验数据进行对比,如图15所示。

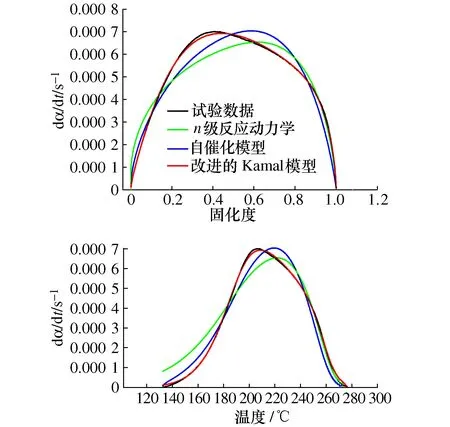
图15 3种模型拟合曲线与试验数据对比

显然改进的Kamal模型更加准确的描述了预浸料体系的固化反应动力学过程,因此我们采用该模型作为这种预浸料体系的固化动力学模型。

4 验证

通过等温试验结果对选取的固化动力学模型进行进一步的验证。利用固化动力学方程对等温固化过程进行模拟计算,为方便对比试验数据和模型数值,取首次达到恒温温度的时刻作为横坐标的起始点,如图16所示。

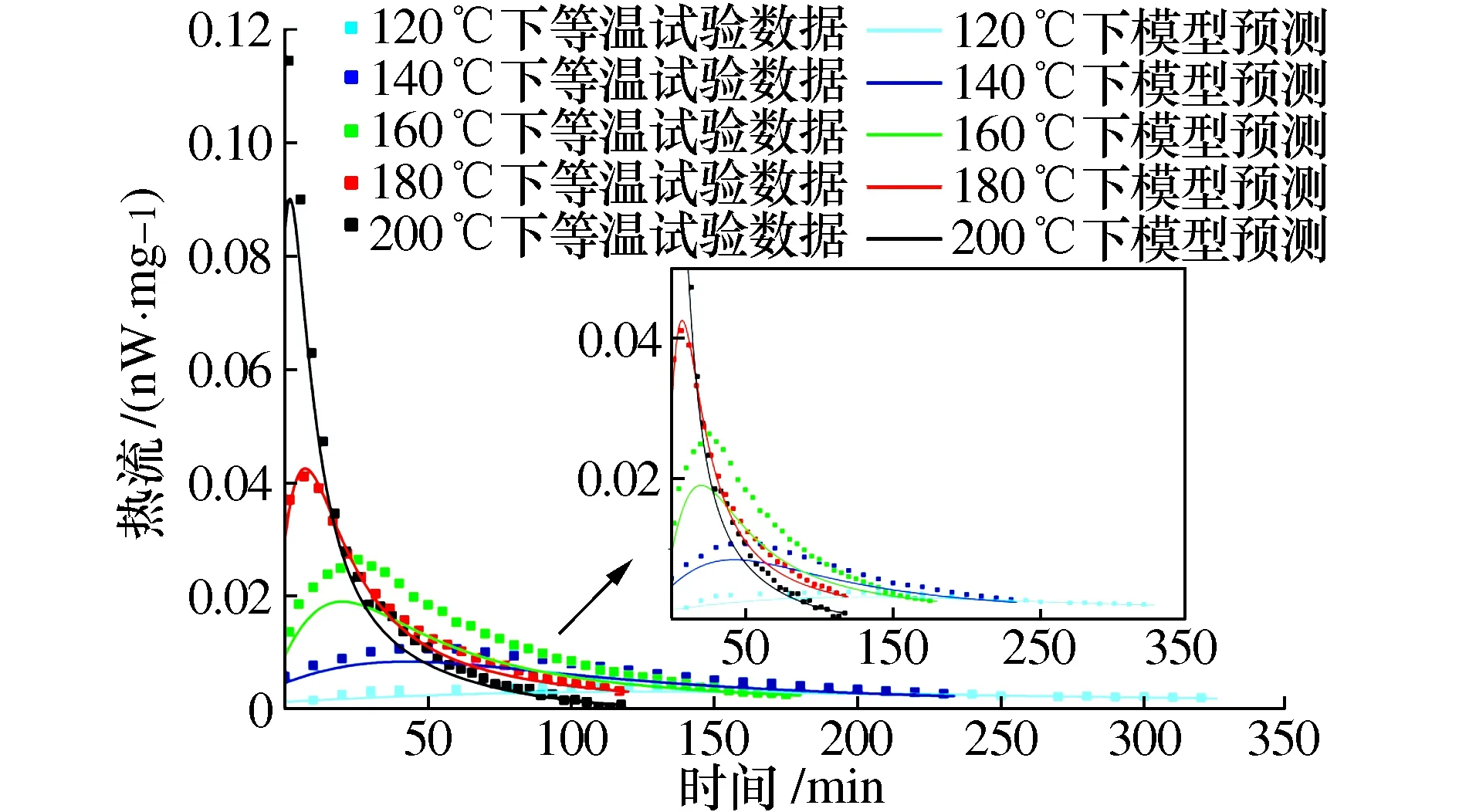
图16 模型等温固化预测与试验结果对比

图中散点代表不同温度下的试验数据,实线为模型拟合数据,可以看到试验值与预测值基本吻合,说明该模型可以准确的预测等温固化过程。

表7中包含了等温固化后试样的残余热量、当前的固化度的测量值以及模型的预测值,试验测量值和预测值近乎相同,进一步说明了模型的准确性。

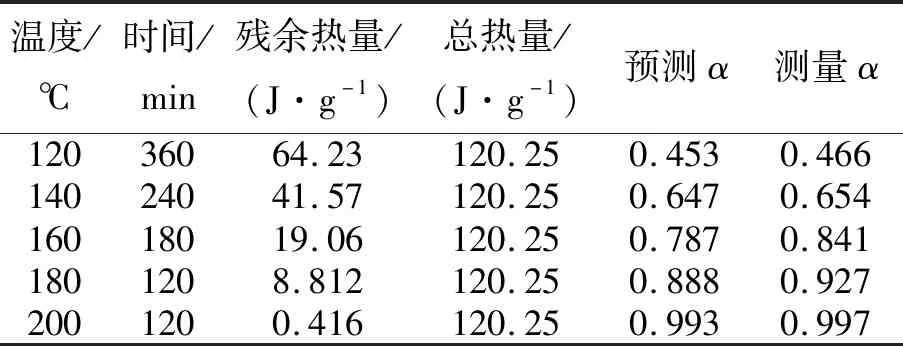
表7 固化动力学模型对等温固化反应的预测

表7中包含了等温固化后试样的残余热量、当前的固化度的测量值以及模型的预测值,试验测量值和预测值比较接近,进一步说明了模型的准确性。

5 结束语

采用动态及等温DSC试验方法研究碳纤维/环氧树脂预浸料体系的固化反应过程,建立了材料玻璃化转变温度随固化度变化的模型。分别采用n级反应动力学模型、自催化模型以及改进Kamal模型3种方法对预浸料体系固化过程进行描述。

对比3种模型发现n级反应动力学模型能够较准确预测反应后期,但是对于前期有着较大的误差;自催化模型则能够较为准确的描述反应前期,对于中后期预测存在较大误差;而改进的Kamal模型则能够更准确的描述整个固化过程。通过等温DSC试验数据对改进Kamal模型进行对比验证,发现拟合结果与试验数据能够很好的吻合,进一步验证了模型的准确性。