WPD和SVM-PSO在微铣刀磨损在线监测中的应用

王二化,刘颉

(1.常州信息职业技术学院 常州市高端制造装备智能化技术重点实验室,江苏常州 213164;2.华中科技大学 水电与数字化工程学院,武汉 430074)

微铣削技术具有加工材料的多样性和三维曲面加工的独特优势,在微观尺度的零部件加工方面具有广泛的应用。然而由于微铣削具有刀具尺寸小、切削速度高且切削不连续的特点,微铣刀磨损迅速,影响产品精度和表面质量。严重的刀具磨损也会引起刀具破损、折断和颤振,造成机床的损伤[1]。因此,亟需提出一种有效的刀具磨损监测方法。前期的研究工作主要包括两个方面:1)直接法:通过数字图像处理技术对铣刀磨损图像进行处理,实现刀具的磨损监测;2)间接法:通过对切削力、振动和声发射信号进行信号处理、特征提取和分类,预测刀具磨损。

直接法主要借助于高精度的高速相机获取铣刀磨损图像,并通过数字图像处理技术获取刀具磨损特征[2-4],利用支持向量机[3]、人工神经网络[5]等算法进行刀具磨损程度的分类。可以看出,直接法通过先进的高速相机可以得到刀具磨损的真实状态,具有较高的精度。但冷却液和切屑不利于得到高质量的刀具磨损图像,此外,加工过程中刀具与工件连续接触,机器视觉难于实时获取切削区域的图像,这就要求刀具与主轴脱离,从而可能引起下一步操作中的刀具错位[6-7]。

为克服直接法出现的问题,一些研究人员提出了基于加工过程传感信号的间接法。间接法主要包括传感器选择、特征提取和特征分类,其中,刀具磨损监测所用传感信号包括切削力[8-10]、振动[9]、声发射[11]及多传感系统[12-13]。由于振动信号与加工过程的紧密联系及安装方便的特点,本研究选择振动信号用于微铣削磨损监测。

通常,有效的特征提取可以提高最终的分类精度。时域[14]、频域[15]和时频域[16-18]特征提取方法可用于加速度信号的处理。其中,具有强大功能的时频域信号处理方法在特征提取中变得非常流行。例如,在经验模态分解(Empirical model decomposition,EMD)中,利用Hilbert-Huang变换获得一系列正交的固有模态函数,然后利用Hilbert谱分析捕获瞬时频率阵列[17]。与短时傅立叶变换(Short time fourier transform,STFT)相比,EMD不需要太多的干扰。然而,由于理论背景较少,模式混合和末端效应的问题仍然存在[19]。此外,STFT通过定义的窗函数使一个长非平稳信号成为许多短平稳信号的叠加[16]。然而,同样形状、尺寸和放大倍数的窗口功能限制了应用范围。STFT的性能主要受定义的窗口函数的影响。低频段和高频段振动信号的计算精度不能同时达到。作为替代方案,使用小波包变换(Wavelet packet transform,WPD)进行信号处理,基函数和分解层数可以自主选择,从而克服了STFT的计算精度问题和EMD的模式混合问题。本文采用WPD提取微铣削加速度信号的磨损特征。

根据得到的微铣削振动信号的磨损特征选择合适的分类方法实现微铣刀磨损程度的识别。与其它分类方法相比,支持向量机(Support vector machine,SVM)[19]已成为非线性数据分类的有力工具。然而,像其他分类算法一样,过拟合和局部最优问题仍然存在。为了解决这些问题,本文采用粒子群算法(Particle swarm optimization,PSO)对SVM的关键参数进行优化,避免初始参数选择的盲目性问题,减少SVM的过拟合和局部最优的问题,提高SVM的识别精度。

综上所述,本文提出了一种基于WPD和SVM-PSO模型的微铣刀磨损的在线监测方法。首先,WPD完成微铣削振动信号的分解,克服了STFT的计算精度问题和EMD的模式混合问题。其次,根据振动信号在初始磨损、轻度磨损、中度磨损、重度磨损和刀具失效状态下的特性,提取小波包关键节点的能量比系数和小波包系数峭度。最后,采用SVM-PSO模型对提取的特征进行分类,并对刀具磨损状态进行识别。

1 研究方法

以微铣削振动信号为研究对象,本文提出了基于WPD和SVM-PSO的微铣刀磨损在线监测方法。首先对微铣削振动信号进行3层WPD分解,得到各个小波包节点的小波包系数;然后计算各个小波包节点的能量比和小波包系数峭度,得到小波包关键节点的能量比系数和小波包系数峭度作为微铣刀磨损的2个特征;最后利用SVM-PSO进行特征分类,实现微铣刀磨损的在线监测。总体研究方案如图1所示。

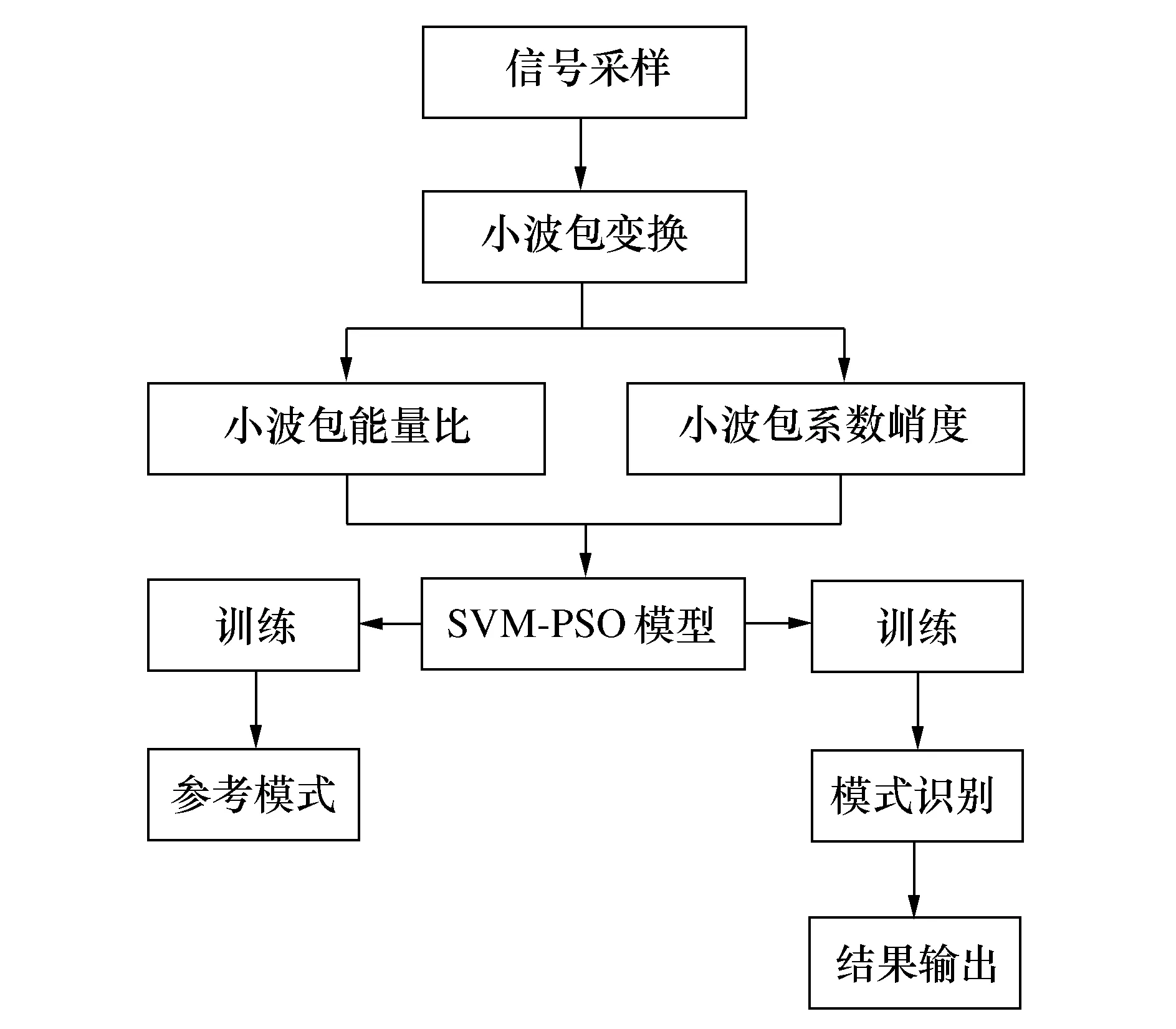
图1 总体研究方案

1.1 小波包变换

小波变换属于时频分析技术,和其它方法相比,小波变换的主要优点是它能同时保证低频和高频信号的高精度,其定义为

(1)

式中：f(t)为待处理的信号;ψu,s(t)为小波;ψ(t)为“母小波”;u和s分别为连续的尺度和位置参数。

和连续小波变换相对应,离散小波变换定义为

(2)

式中：j和k同为整数;u和s同为常数。

为了定义小波包,令:

ψ0=(x)

(3)

ψ1=ψ(x)

(4)

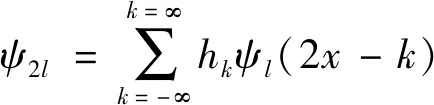
(5)

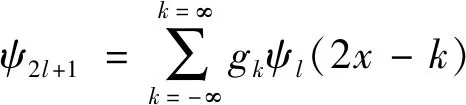
(6)

将函数{ψn}定义为尺度函数ψ(x)的小波包。小波包分析结果包括分别由尺度函数和小波函数组成的子空间,即

(7)

假设对信号进行3层小波包分解,分解的子空间个数为21+22+23=14,分解结果如图2所示。

图2 小波包树与节点数据

1.2 SVM-PSO

SVM是一类按监督学习方式对数据进行二元分类的广义线性分类器,其决策边界是对学习样本求解的最大边距超平面。可以通过数据点描述,即

w·x+c=0

(8)

支持向量所在的虚线为

f±1(x)=w·x+c=±1

(9)

最优超平面的边际(边际就是某一条线距离它两侧最近的点的距离之和)可以表示为2/‖w‖,最优超平面可以通过求解2/‖w‖的最大值或‖w‖的最小值得到,约束条件为

(10)

但有些数据样本用于分类的超平面没法找到,这就需要在核函数的辅助下将SVM扩展到非线性数据的分类。4种常用核函数如表1所示。

表1 4种核函数及其数学表达式

由于SVM可以用于非线性数据的分类,近年来,SVM已成为解决模式分类和回归问题的主要算法之一。在SVM模型中,网格搜索法通常用于SVM模型的多参数调试,以提高SVM的分类精度。然而网格搜索法本身存在的问题限制了它的应用范围,如果网格足够小,分类精度高,但参数调试花费时间过长,特别是有超过3个参数需要调整的情况;如果网格增大,计算效率明显提高,但又很难找到SVM模型的最优参数,如何平衡计算精度和计算效率是一个亟待解决的问题。

为解决这样的两难问题,通过PSO取代网格搜索法实现SVM关键参数的优化,PSO算法容易编程,并且不需要遗传算法的编码和解码过程,具有更高的计算精度和效率。在PSO算法中,影响粒子飞行速度3个因素分别为:突进部分、认知部分和社会部分。假设全局最优位置Pg=(pg1,pg2,…,pgm),同时第i个粒子的速度Vi=(vi1,vi2,…,vim),每个粒子的新速度和位置分别为:

(11)

(12)

式中：c1和c2是两个加速度系数;w是控制粒子群全局搜索和局部搜索能力的惯性因子;r1和r2是[0,1]之间的任意两个数;αi是第i个粒子的当前最好位置。

将分类精度作为目标函数,PSO用来优化SVM模型的输入参数,优化过程的流程图如图3所示。

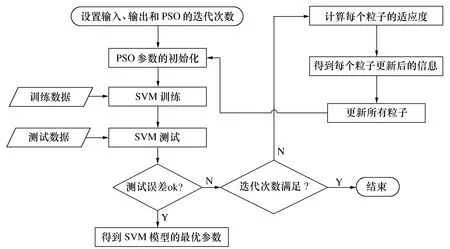
图3 SVM-PSO的流程图

2 实验方法

为了验证本文提出的微铣刀磨损在线监测方法,本研究在五轴加工中心Huron K2X5完成了一系列模具钢NAK80的切削实验,如图4所示。所用刀具为直径0.5 mm、螺旋角30度的硬质合金微铣刀。毛坯尺寸70 cm×50 cm×20 cm;三向加速度传感器1A110E:灵敏度10 mv/m/s-2,频率范围(±10%)0.5～10 000 Hz;通过DH5922D数据采集系统获取工件的振动信号。

图4 实验装置

本实验总共用了36把微铣刀,每把刀加工时间均为18 min,全程采集振动信号,并每隔3 min将刀具拆下来,通过影像仪获取刀具切削部位的图像。主要切削参数如表2所示。

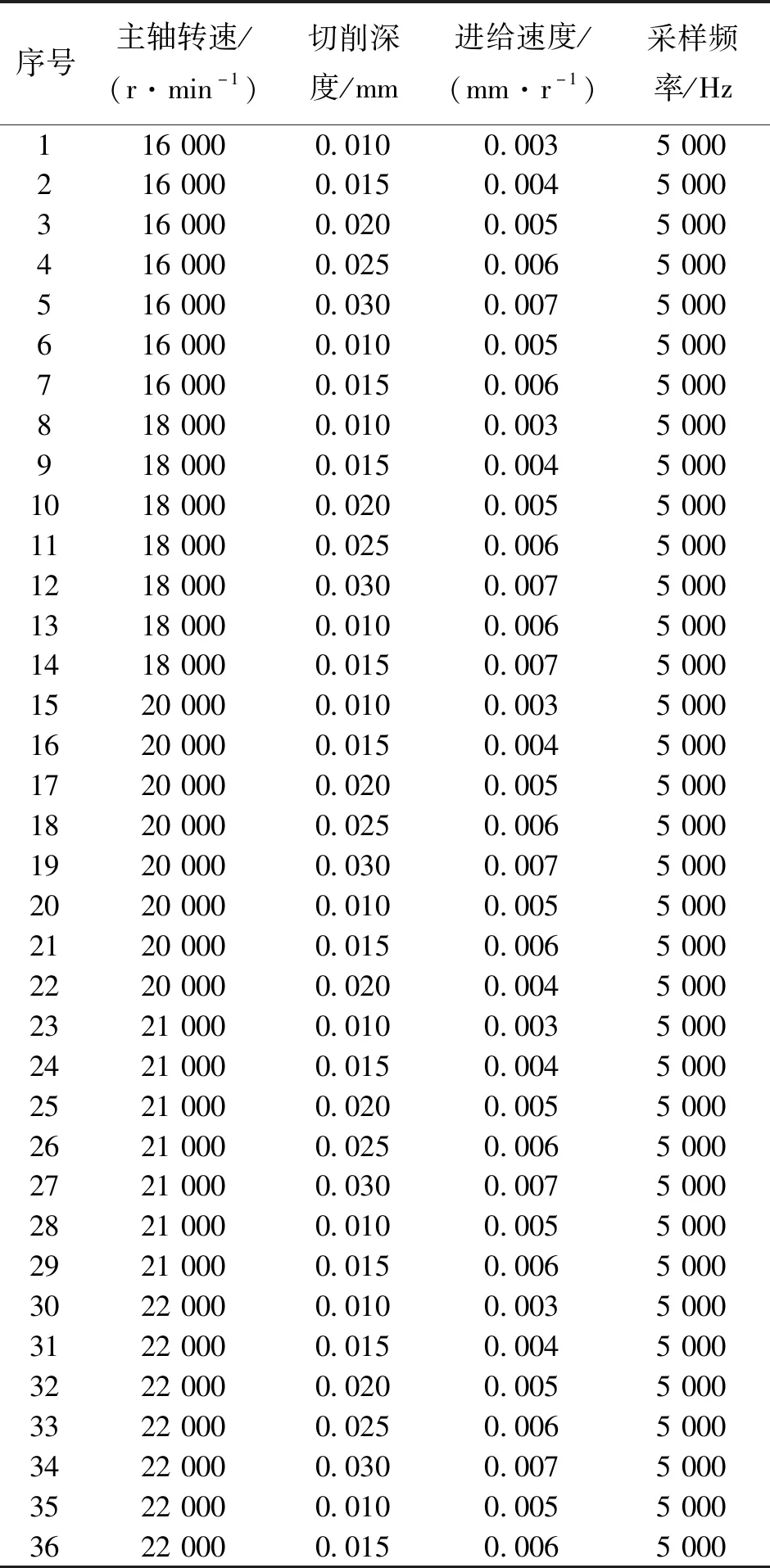
表2 模具钢NAK80的微铣削切削参数

由于机床x,y轴方向的振动信号较弱,选用z轴方向(机床主轴方向)的振动信号进行研究,采集得到的时域波形如图5所示。

图5 机床z轴方向的加速度信号

图5显示,直线AB将整个振动信号分成左右两个部分,左边表示未切削时刻的振动信号,右边表示切削时刻的振动信号,由于未切削时刻的振动信号几乎不包含刀具磨损的任何信息,后续的信号处理和特征提取所对应的均是切削时刻的振动信号。

通过影像仪得到了加工时间为0～15 min的微铣刀切削刃图像如图6所示。

图6 微铣刀切削刃磨损图像

图6显示,随着加工过程的持续进行,微铣刀磨损程度不断提高。不考虑新刀状态,将微铣刀磨损程度分为5种等级,分别为:初始磨损(3～6 min)、轻度磨损(6～9 min)、中度磨损(9～12 min)、重度磨损(12～15 min)和刀具失效(15 min以上)。

3 特征提取

使用“meyr”小波对刀具失效状态的加速度信号进行3层小波包分解,计算结果及小波包系数分别如图7和图8所示,其中,切削条件:主轴转速:20 000 r/min;进给速度:0.004 mm/r;切削深度:0.02 mm。

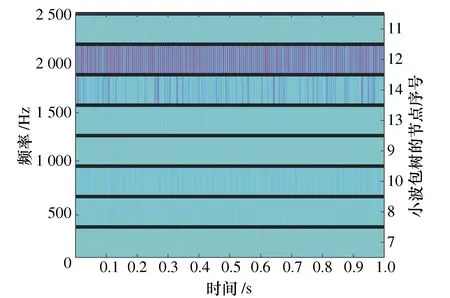
图7 微铣削切削时刻加速度信号的小波包分解

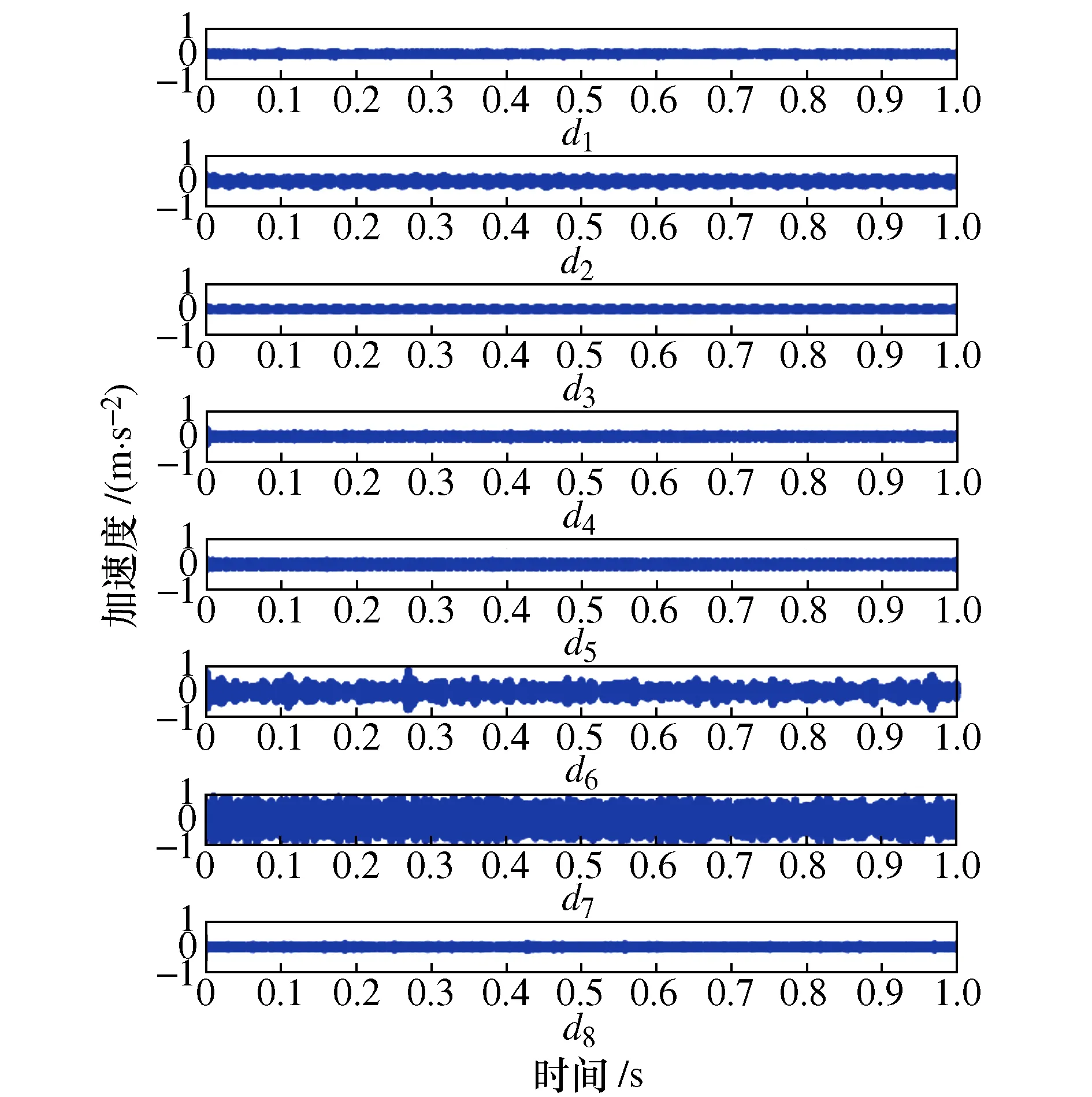
图8 切削时刻加速度信号的小波包系数

图7和图8显示,振动信号的小波包树节点12(1 875～2 187.5 Hz)具有最大的频率成分,其次是节点14(1 562.5～1 875 Hz)。另外,振动信号的频率成分不随时间变化,具有稳定的特性,只有外部条件改变,如刀具磨损,才可能引起频率成分的改变,因此,本文将小波包关键节点的能量比系数和均方根系数作为微铣刀磨损特征。

3.1 小波包能量比

为了表达方便,按照从低到高的顺序重新排列小波包节点序号,其中,节点1频率范围:0～312.5 Hz,节点2频率范围:312.5～625 Hz,…,节点8频率范围:2 187.5～2 500 Hz。

(13)

可以得到第m层所有节点的小波包总能量Em为

(14)

(15)

根据以上计算方法,得到5种磨损状态的小波包节点的能量比如图9所示。

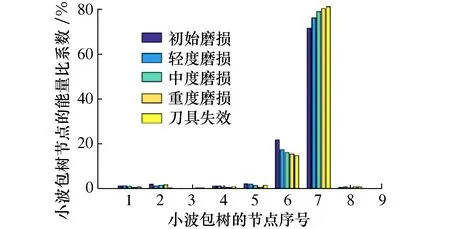
图9 微铣刀5种磨损状态的能量比

图9表明,随着刀具的不断磨损,节点6的能量比持续减小,同时,节点7的能量比不断增加,其它节点的能量比幅值较小,且变化规律不明显。由于小波包树节点6和7的能量比变化幅值不大,为了进一步提高微铣刀磨损特征的识别度,设置微铣刀的磨损特征为

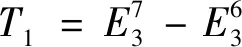
(16)

经过简单计算,结果如图10所示。

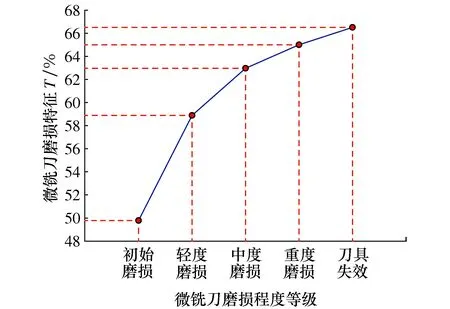
图10 微铣刀磨损特征T1与磨损程度的关系图示

由图10可以看出,由于微铣刀磨损特征T1综合了小波包树节点6和7的变化幅值,具有更高的识别精度。

为提高微铣刀磨损特征T1的通用性,保持进给速度和切削深度不变,只改变主轴转速,可以得到主轴转速对微铣刀磨损特征T1的影响情况。根据同样的方法,可以分别得到进给速度和切削深度对微铣刀磨损特征T1的影响情况。计算结果如图11～图13所示。

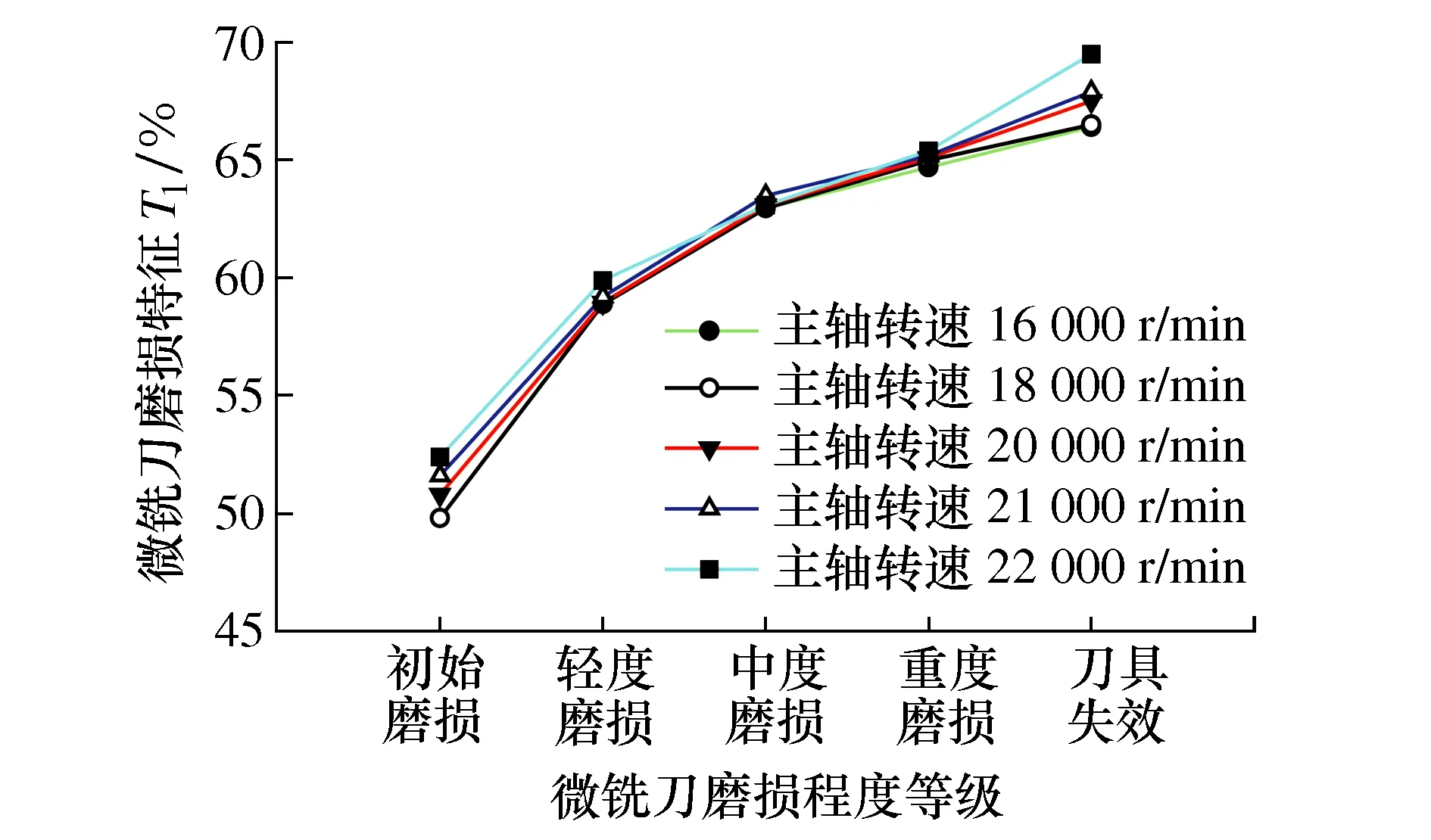
图11 主轴转速对微铣刀磨损特征T1的影响

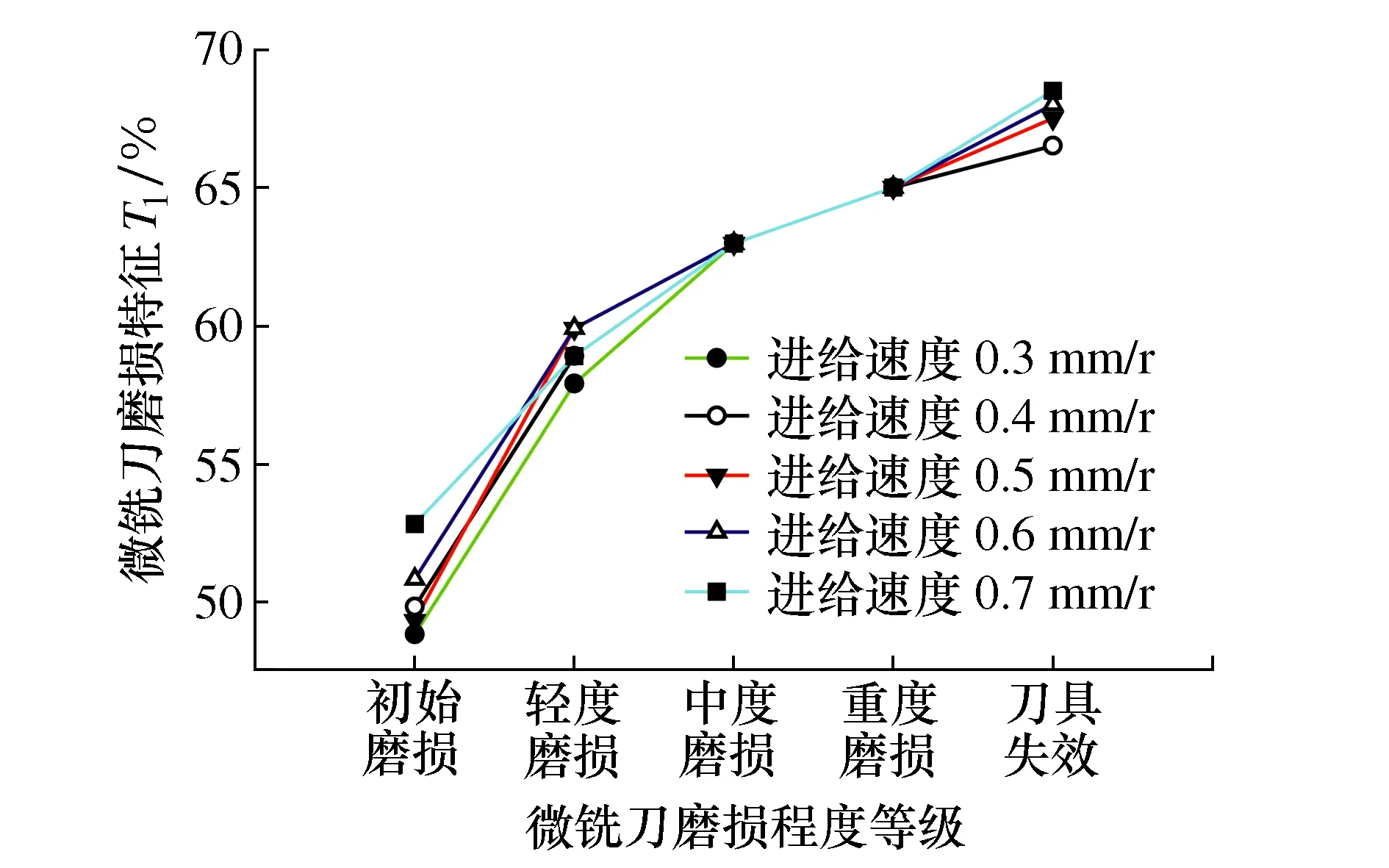
图12 进给速度对微铣刀磨损特征T1的影响

图13 切削深度对微铣刀磨损特征T1的影响

由图11～图13可得,各种切削参数对微铣刀磨损特征T1具有一定的影响,尤其是切削深度的变化导致轻度磨损状态与中度磨损状态,以及中度磨损状态与重度磨损状态之间的区分度不够明显,这就需要通过合适的分类算法来实现各种磨损状态的分类。

3.2 小波包系数峭度

假设采样的加速度信号为x=[x(1),x(2),…,x(n)],n表示信号长度。加速度信号x的峭度定义为[20]。

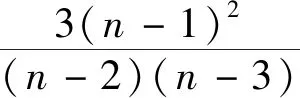
(17)

可以看出,峭度是加速度信号的4阶累积量,而高斯信号的高阶累积量恒为0,因此,高斯信号的归一化峭度值为0。

在微铣削过程的初期,刀具磨损不太严重,振动信号接近于正态分布,峭度值较小,随着刀具磨损程度的不断提高,振动信号渐渐远离整体分布,导致峭度值不断增加。

由于微铣削加工过程影响因素较多,振动信号较为复杂,为避免其它因素的影响,本文将时域信号的峭度概念引入到小波包系数的分析当中,提出了小波包系数峭度的概念,根据式(17)可以得到各种磨损状态下小波包树节点的小波包系数峭度,并对数据进行归一化,结果如图14所示。

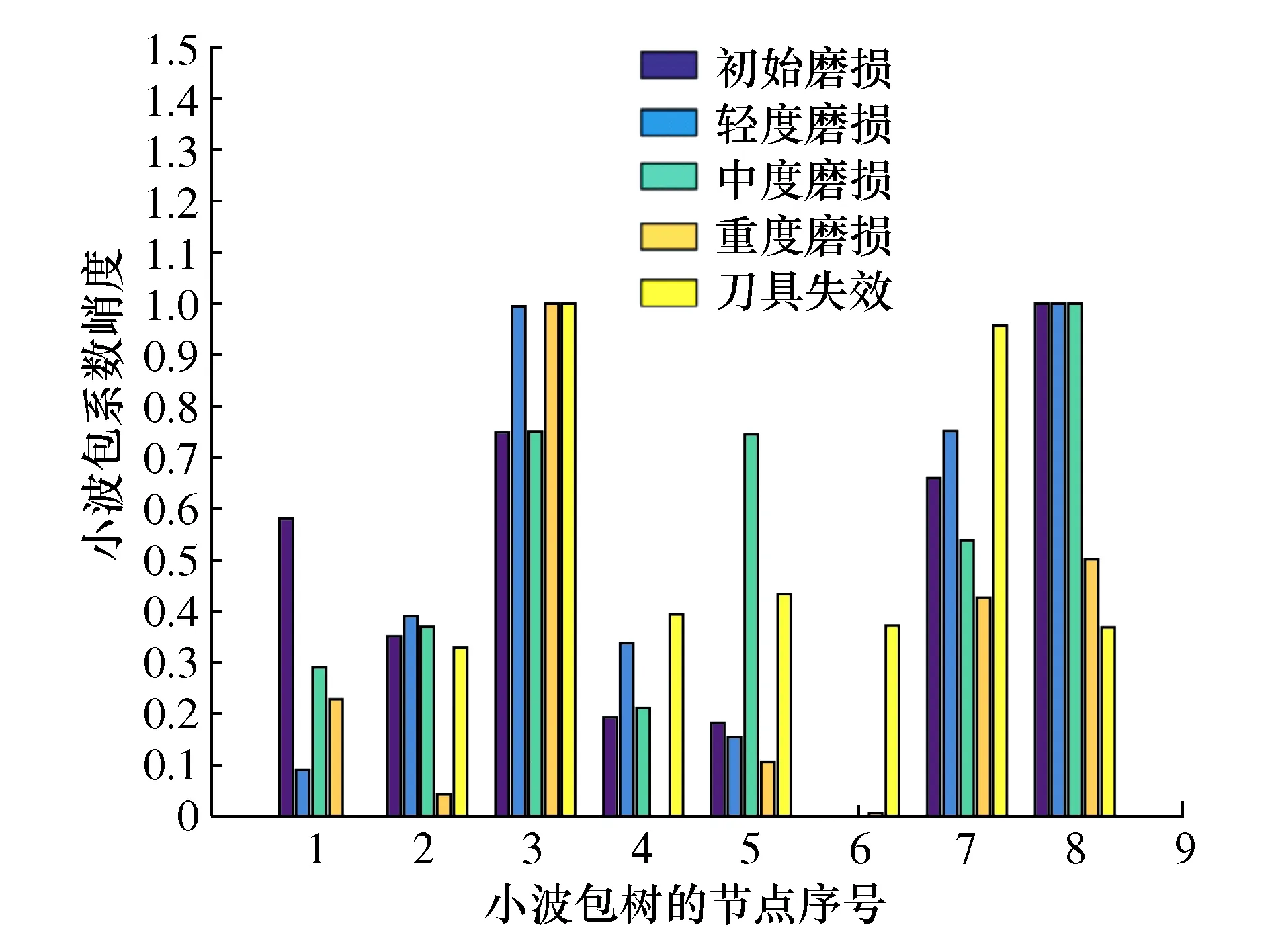
图14 微铣刀5种磨损状态的小波包系数峭度

由图14可以看出,和其它小波包树节点相比,关键节点7的小波包系数峭度具有最高的识别度,因此,将其作为微铣刀磨损的第2个特征,用符号T2表示。

为了解小波包系数峭度的通用性,利用和小波包能量比系数一样的方法,可以得到主轴转速、进给速度和切削深度对小波包系数峭度的影响情况分别如图15～图17所示。

图15 主轴转速对微铣刀磨损特征T2的影响

图16 进给速度对微铣刀磨损特征T2的影响

图17 切削深度对微铣刀磨损特征T2的影响

由图15～图17可以看出,切削参数的改变导致微铣刀磨损特征T2出现不同程度的波动,但对各种磨损状态的识别没有太大影响。

综上所述,本文提出的两个微铣刀磨损特征具有较高的识别度,能够满足不同切削参数工况下微铣刀磨损监测的需要。

4 特征分类及性能分析

基于已提取的2个微铣刀磨损特征,通过SVM-PSO进行特征分类。首先得到每种磨损状态400组,共2 000组不同切削参数工况下的振动信号。随机选择每组磨损状态中的320组共1600组数据用于训练,剩下的400组数据用于测试。然后根据以上计算方法得到每组数据的2个微铣刀磨损特征。

通过SVM-PSO对已获取的磨损特征进行分类,具体步骤如下:

1) 特征数据输入;

2) 数据处理:标准化和正则化;

3) SVM核函数的分析和选择;

4)基于PSO的SVM关键参数调试。

SVM-PSO的输入为两个微铣刀磨损特征T1和T2,输出为5个微铣刀磨损状态,分别为:初始磨损(000),轻度磨损(001),中度磨损(010),重度磨损(011),刀具失效(100)。选择MATLAB 2018a作为特征分类的软件。

经过多次试验,选择的多项式核函数为

kxy=(γxy+r)d

(18)

式中：r为常数;x为特征数据;y是标签数据;γ和d为两个待调试的关键参数。γ和d对SVM的分类精度具有重要影响,初始值分别为0.5和2。粒子群的例子数量为50,PSO的其它参数设置如表3所示。

表3 PSO的参数设置

为验证本文提出的微铣刀磨损在线监测方法的整体性能,将其运算结果与基于网格搜索法(Grid searching,GS)的SVM及不带优化算法的SVM模型进行对比。其中,网格搜索法中γ和d的初始值和网格尺寸分别为:[0,0.1]和[0,0.5]。同时,通过不带优化算法的SVM进行刀具磨损状态的分类,计算结果如图18所示。

图18 SVM,SVM-PSO和SVM-GS的计算结果

图18显示:SVM-PSO具有最高的预测精度,SVM精度最低,SVM-GS的预测精度仅次于SVM-PSO。主要因为SVM的参数设置没有经过优化过程,参数完全依靠经验进行选择,很难找到最优的参数;SVM-GS通过网格搜索方法优化SVM的两个关键参数,和SVM相比,精度有很大提高,但GS自身的初始参数和网格尺寸的设置仍然需要丰富的工程经验,面对一个新的对象很难快速确定左右的参数。此外,可以看出,由于SVM没有附带的优化算法,计算时间最短,SVM-GS需要计算所划分网格上的每一个点的分类精度,用时最长,SVM-PSO计算时间介于SVM和SVM-GS之间,和SVM-GS相比具有较大优势。综合比较发现,和SVM以及SVM-GS相比,SVM-PSO在分类精度和计算时间方面具有较大的综合优势,能够满足微铣刀磨损在线监测的精度和实时性方面的要求。

为了解单一磨损特征对分类精度和计算时间的影响,先分别将T1、T2及T1和T2作为SVM-PSO模型进行计算,结果如图19所示。

图19 微铣刀磨损特征选择对计算结果的影响

由图19可以看出,和2个特征相比,单一特征的计算时间明显减少,计算精度也有显著降低。主要因为单一特征只能反映振动信号某一方面的特征,不利于微铣刀磨损特征的精确识别。

训练样本的数量直接影响模型的分类精度和计算时间,因此,将训练样本数量分别设置为1 000,1 200,1 400,1 600和1 800,分别进行计算,结果如图20所示。

图20 训练样本数量对计算结果的影响

由图20可以看出,随着训练样本数量的增加,计算时间直线上升,计算精度整体上也有明显提高,但训练样本数量达到1800时,计算精度变得不太稳定。主要因为训练样本数量越多,训练出来的SVM-PSO模型越精确,但如果测试样本过小,就会出现较大的随机性,造成分类精度的不稳定。

5 结论

为解决刀具的过度磨损进而损伤工件,以及刀具使用不充分造成浪费的问题,本文提出了一种基于WPD和SVM-PSO的微铣刀磨损在线监测方法。研究表明,提出的2个微铣刀磨损特征辨识度高,并且基本不受切削参数的影响。和SVM-GS模型相比,本文提出的SVM-PSO分类算法在分类精度和计算效率方面具有综合优势,对其它微铣刀磨损方法具有一定的参考价值和借鉴意义。此外,和两个特征相比,单一特征的计算时间明显减少,计算精度也有显著降低。随着训练样本数量的增加,计算时间直线上升,分类精度也会稳步提高,但训练样本数量过多,会造成分类精度的不稳定。