基于新息突变约束的自适应卡尔曼滤波研究

2022-07-16邓义廷

压电与声光 2022年3期

邓义廷，方针,2，彭慧，冯伟，刘宇

(1.重庆邮电大学自主导航与微系统重庆市重点实验室，重庆 400065; 2.中国电子科技集团公司第二十六研究所，重庆 400060)

0 引言

微惯性测量单元(MIMU)虽已广泛用于无人机、吊舱、惯性定位导航等各领域，但是微机电系统(MEMS)惯性器件的低精度和高漂移限制了系统的测量精度和性能，因此，MEMS陀螺仪的误差分析和校正不补偿具有重要意义[1-4]。

MEMS陀螺仪误差包括系统误差和随机误差[5]。系统误差能够使用高精度转台设备校准，以减小对测量结果的影响[6]，而随机漂移误差是MEMS陀螺仪在外界因素的影响下偏离实际方向产生的，并随时间和周围环境条件不断变化，难以用标定进行处理[7]。随机误差是提高MEMS惯性器件精度的主要限制因素之一。目前用于MEMS惯性器件误差分析的方法主要有时间序列分析法、Allan方差分析法和小波神经网络等[8]。

本文使用Allan方差分析陀螺仪的随机噪声，并对MEMS陀螺仪的随机误差进行了时间序列分析和建模。然后在经典卡尔曼滤波器的基础上加入衰减因子和基于新息突变约束的误差矩阵进行自适应估计补偿，再结合MEMS陀螺仪试验，并利用Allan方差对滤波前后的数据进行对比分析。

1 Allan方差分析原理

Allan方差分析常用于定量地对陀螺仪各项随机误差进行辨识[9]，作为对MEMS陀螺仪滤波前后评价其性能的重要指标。

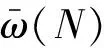
(1)

Allan方差定义为

(2)

MEMS陀螺仪随机噪声主要包括量化噪声、角度随机游走、零偏不稳定性、速率随机游走及速率斜坡5种。本文使用Allan方差法进行定性分析[9-10]，各种随机误差源与Allan方差的关系为

(3)

用最小二乘法对Allan方差的曲线进行拟合，求得相应参数。MEMS陀螺仪的随机误差的的计算公式和Allan方差对数图如表1所示[9]。

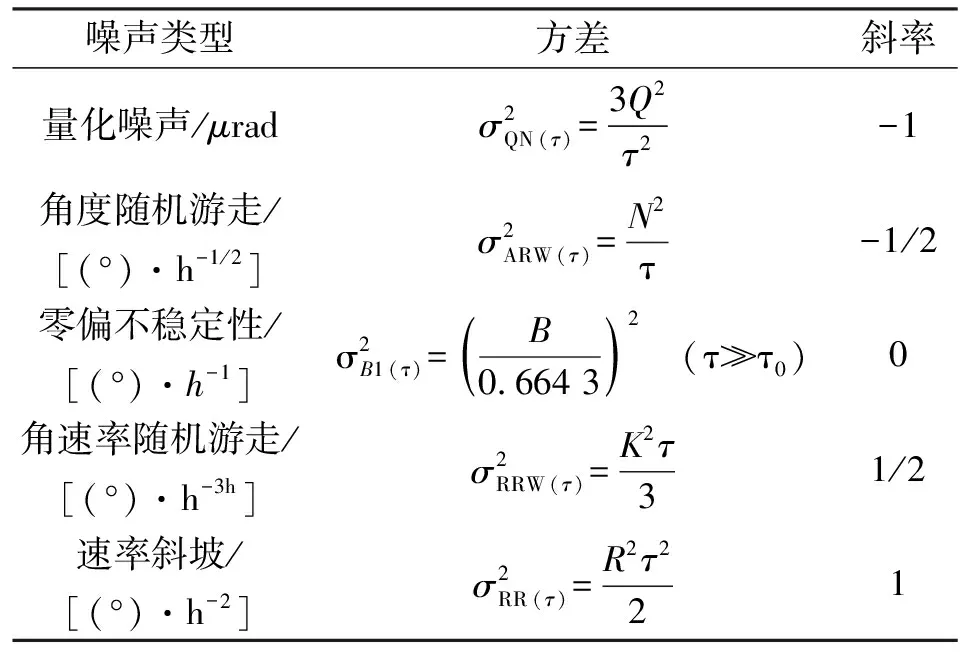
表1 Allan分析与5种噪声的对应关系

Allan分析不一定能得出量化噪声和速率斜坡结果，而由于MEMS陀螺仪中的随机误差主要包括角度随机游走、零偏不稳定性和随机噪声角速率随机游走，因此，重点关注这3个误差。另外再引入标准差判断数据的离散性。

2 时间序列分析与建模

时间序列分析模型主要有自回归模型(AR)、滑动平均模型(MA)及自回归滑动平均模型(ARMA)。首先对采集的数据进行预处理，再判断模型类别，估计模型参数[11]。

2.1 时间序列模型的确定

数据经去粗差、去趋势项及去周期项等预处理后，可以进行时间序列模型建模[12]。通过自相关函数图(ACF)和偏相关函数图(PACF)的“拖尾/截尾”性质识别时间序列的模型结构[13]。对试验所用1号MEMS陀螺仪进行自相关和偏自相关检测，如图1、2所示。

由图1、2可得出试验所用1号MEMS陀螺仪的ACF图和PACF图都是拖尾，判断对该陀螺仪建模采用ARMA模型。平稳、正态时间序列xk的ARMA(p,q)模型[8]为

(4)

式中：φi(i=1,2,…,p)表示自回归系数；θi(i=1,2,…,q)表示滑动平均系数；εs,εt为新息；E(εt)是εt的方差；E(εtεs)，E(Xsεt)代表期望。

2.2 ARMA模型定阶及参数确定

首先要确定ARMA模型的阶数。常用的判断方法有AIC准则、BIC准则、FPE准则及新息值等[14]。此次建模选用AIC、BIC准则判定模型阶数。

赤池信息量准则(AIC)是估计随机序列模型阶次的一种优良的度量[14]:

(5)

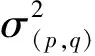
贝叶斯信息准则(BIC)与AIC类似，用于模型阶数的选择[14]:

BIC(p,q)=-2ln(L)+(p+q)ln(N)

(6)

式中：L为最大似然函数；N为样本总数。

经过AIC和BIC准则计算，得到本文使用的1号MEMS陀螺仪的ARMA模型为ARMA(3,2)。

采用自回归逼近法估计[11]本文ARMA模型参数。估计参数为：φ1=0.138 11，φ2=0.158 41，φ3=-0.110 56，θ1=0.273 14，θ2=-0.180 75。1号MEMS陀螺仪x轴ARMA模型的表达式为

xk=0.138 11xk-1+0.158 41xk-2-

0.110 56xk-3+εk-0.273 14εk-1+

0.180 75εk-2

(7)

3 卡尔曼滤波器设计

基于式(7)建立ARMA(3,2)模型，采用卡尔曼滤波对MEMS陀螺仪随机误差进行补偿。由ARMA(3,2)模型得到1号MEMS陀螺仪的状态方程和量测方程可表示为

(8)

式中：Ak/k-1表示系统的状态转移矩阵；Xk-1=[xk-1xk-2xk-3]T；Bk/k-1表示系统的噪声矩阵；Qk-1表示k-1时刻的系统噪声；Hk为k时刻的量测矩阵；Vk为k时刻的量测噪声。采用文献[14]中的设置方法得到滤波器参数为

(9)

(10)

(11)

传统的卡尔曼滤波递推方程[15]为

(12)

有时测试的数据中含有一些异常值，其量测方程为

zk=Hkxk+Vk+sigk

(13)

式中sigk为k时刻的异常测量值。含有异常值的新息为

(14)

误差矩阵为

(15)

矩阵每一行表示对MEMS数据新息的约束参数：

yk(k)=ci1+ci2yk(k-1)+…+cijyk(k-j)

(i=1,2,3;j=1,2,…,n)

(16)

每个参数的值随输入信号而变化，通过对短时间的新息进行曲线拟合，再通过互补对新息进行更新，其中曲线参数采用递推最小二乘法进行参数更新。

同时考虑到被测噪声参数不稳定的特点，在滤波算法中加入了衰减记忆系数，采用衰减记忆加权算法自适应估计，减小旧值对滤波算法的影响[4]。引入新息误差矩阵和衰减记忆系数之后的卡尔曼滤波算法为

(17)

式中b(0

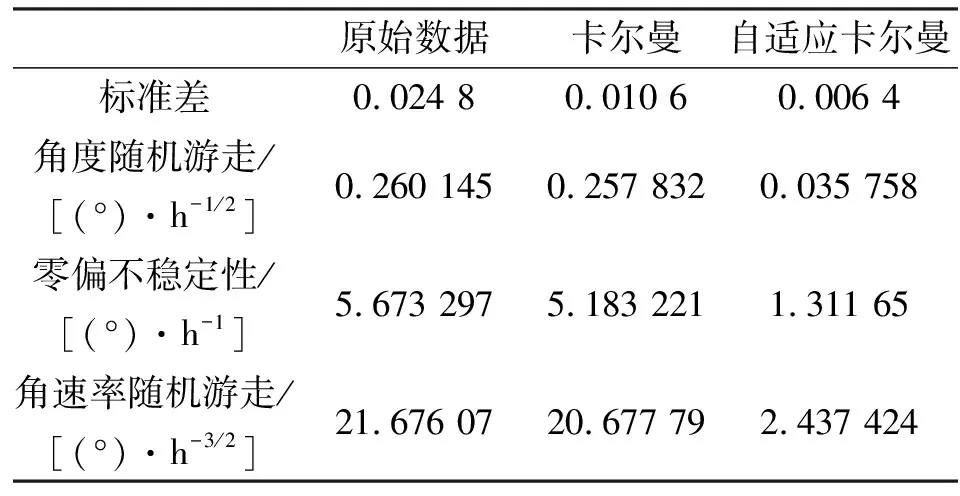
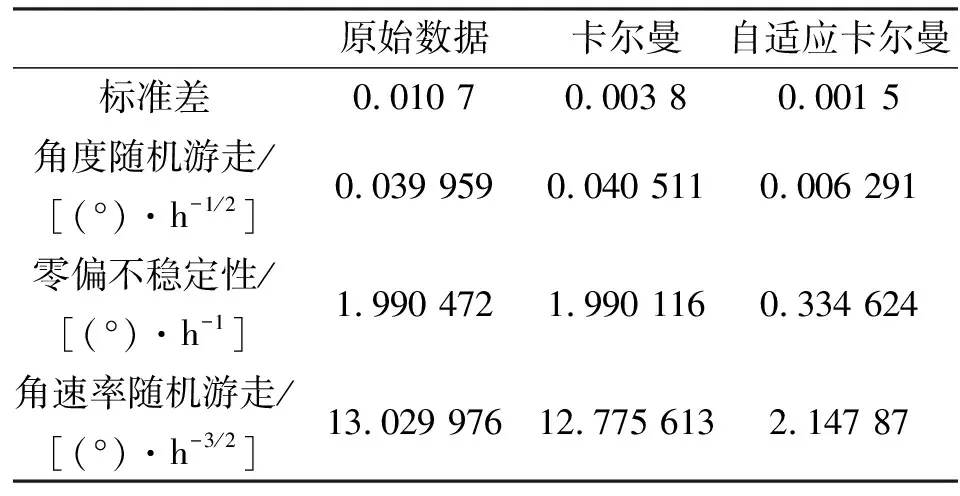
4 数据分析和结果验证

实验中采用实验室自研1号和2号MEMS陀螺仪进行测试，转台采用我国自主研发制造的特定型号3轴速度位置转台，如图3所示。采样频率为200 Hz，用于测试滤波方法的可靠性和补偿效果。

4.1 1号MEMS陀螺仪测试

4.1.1 1号MEMS陀螺仪静态测试

进行数据采集时，将1号MEMS陀螺仪固定到三轴速率转台上，调至水平，实验室温控制在常温。在室温、零激励条件下采集2 h静止数据，选取稳定部分进行滤波处理。部分数据测试结果如图4、5所示。

由图4、5可见，KF和自适应KF滤波后的数据起伏明显变小，但KF滤波的结果存在较多明显尖峰，即突变值。自适应KF引入了新息突变约束矩阵，新息在补偿前后有明显区别，对数据的突变值有很好的抑制效果，相比之下数据更平滑，不存在明显尖峰。由表2标准差对比可以看出，滤波前后的数据发生突变的概率减小，角度随机游走精度提高0.96倍和9.13倍，零偏不稳定性精度提高1倍和9.84倍，角速率随机游走精度提高2.72倍和26.74倍。

表2 原始数据与滤波结果指标比较

4.1.2 1号MEMS陀螺仪动态速率测试

试验流程类似于静态试验，MEMS陀螺仪固定后，在三轴转台30(°)/s的激励下进行数据采集。其建立的ARMA(3,2)模型为

xk=0.131 37xk-1-0.708xk-2+0.629 18xk-3+

εk+0.472 85εk-1-0.656 87εk-2

(18)

测试结果如图6所示。

由图6可见，原始数据波动较大，导致卡尔曼滤波后也有小幅波动，但自适应滤波后结果较平滑，新息补偿前后也有很大区别，滤波后突跳减少。由表3标准差对比可以看出，滤波前后数据发生突变的概率减小，角度随机游走精度提高1倍和7.28倍，零偏不稳定性精度提高1.09倍和4.33倍，角速率随机游走精度提高1.05倍和8.89倍。

表3 原始数据与滤波结果指标比较

4.2 2号MEMS陀螺仪测试

4.2.1 2号MEMS陀螺仪静态测试

采用相同的处理过程对2号MEMS陀螺仪进行处理，建立ARMA(3,1)模型，其表达式为

xk=0.063 78xk-1-0.166 94xk-2+

0.237 99xk-3+εk-0.124 52εk-1

(19)

最终测试结果如图7、8所示。

根据图7、8可以看出，2号MEMS陀螺仪的测试结果和1号的测试结果基本相同。数据变化更平缓，基本不存在突变值。由表4可见，滤波后标准差明显减小，角度随机游走精度提高0.98倍和6.35倍，零偏不稳定性精度提高1倍和5.96倍，角速率随机游走精度提高1.02倍和6.07倍。

表4 原始数据与滤波结果指标比较

4.2.2 2号MEMS陀螺仪动态速率测试

同1号MEMS陀螺仪在三轴转台上采用30(°)/s的激励进行数据采集。建立的ARMA(3,1)模型为

xk=0.167 68xk-1-0.070 765xk-2+

0.223 29xk-3+εk-0.444 82εk-1

(20)

测试结果如图9所示。

由图9可见，与原始数据和卡尔曼滤波后数据波动相比，自适应滤波后数据波动减小，新息补偿前后也有很大区别，滤波后突跳减少。由表5标准差对比可以看出，滤波前后的数据发生突变的概率减小，角度随机游走精度提高1.09和3.19倍，零偏不稳定性精度提高1.21和8.99倍，角速率随机游走精度提高1.04和5.08倍。