顾客延时离开的共享车位预订控制策略研究

张利凤, 慕银平, 靖富营

(1.成都大学 旅游与文化产业学院,四川 成都 610106; 2.电子科技大学 经济与管理学院,四川 成都 611731; 3.重庆工商大学 智能制造服务国际科技合作基地,重庆 400067)

0 引言

随着汽车保有量的增加，停车难问题日益凸显。为缓解停车难问题，各地政府开始倡导共享闲置车位。如2017年太原市发布的《关于进一步推动太原市“互联网+停车服务”的指导意见》指出，办公区停车位白天紧张，夜间闲置，而居住区则相反，因此可采取错时停车，实现车位共享。虽然车位共享既为平台和车位拥有者带来了收益，也提高了车位利用率，但是居民在使用共享车位时，却出现了未按约定时间驶离的现象。这一现象导致共享车位的推行遭遇阻力。

实际中，车位共享平台与私家车位拥有者合作，将车位的空闲时段进行回购后，提供给需要车位的顾客[1]。共享平台首先发布车位空闲信息并接受顾客的预订。当预订周期结束，进入服务周期时，预订用户可能由于某些特殊原因导致不能按时离开。此时，平台将面临后一位到达的预订顾客无车位可停的风险，从而面临较大的损失。因此，本文需解决的问题为：面对预订顾客有延时行为时，平台如何制订预订策略，既能保障平台的收益也能减少停车时间的冲突。

私家车的普及导致了停车位的稀缺，因此车位的预约分配面临着挑战。针对传统车位预约分配的文献，主要是以最大化收益为目标构建整数规划模型以决策是否应该接受顾客的预订。许多学者基于此，分别构建静态[2～4]和动态[5,6]的优化模型对车位的预订分配进行了研究；Schlote等基于顾客的停车意愿与车位的空置率相关的情形下，将研究从单个停车场拓展到了多个停车场的车位动态分配问题[7]；除此之外，部分研究基于停车资源使用者间的竞争关系，构建了博弈模型对车位的分配进行了研究[8,9]。

为缓解停车难问题，车位共享逐渐出现。关于共享车位分配的研究文献较少，Shao等首次基于供需信息确定的前提下，构建整数规划模型对共享车位预订的静态分配问题进行研究[10]；林小围等基于动态的车位预订供需信息，以停车场利用率最大化为目标构建整数规划对共享车位的分配问题进行研究[11]；Chou等基于需求随机的情形下，以最大化停车场收益为目标，研究了共享车位动态预订控制问题[12]； Wu等通过构建非线性规划模型研究了位置和服务质量决策问题，并设计启发式算法求解模型[13]；Yan等构建了一种实时预约方式，并提出了多对一的匹配机制，以更好地利用稀缺的停车资源[14]。上述车位的预约分配问题均假定顾客会按时离开。在实际中，预约顾客可能因为突发情况导致未按照预订时间离开，此时将可能导致停车时间冲突。

针对共享时间冲突的研究，李涛和关宏志为避免小区内部使用者和外部使用者的时间相冲突，构建优化模型研究了如何实施共享停车[1]；Guo等通过构建高斯混合模型求解了平台的最大回购量，并通过数值仿真得到了避免时间冲突下的共享终止时刻[15]；路扬等以共享时间不冲突为约束条件讨论了共享车位的供需匹配问题[16]。上述研究是以共享车位的时间不冲突作为约束条件探讨车位的匹配问题，而Aydina等针对酒店预订顾客存在延长停留时间的问题进行研究[17]。由于酒店可以拒绝延时申请，因此酒店不会面临时间冲突，而本文将研究因顾客延时离开导致时间冲突情形下的共享车位预订控制策略。

1 随机动态规划模型的构建

实施车位共享时，平台将面临两个阶段：预订阶段和服务阶段。在预订阶段，平台决策是否接受顾客的预订；在服务阶段，平台将车位提供给预订顾客。若共享平台期初回购的车位数量为Q[1,15]，首先将预订阶段离散化为τ个周期，每个周期最多允许一个预订到达[17,18]，再将服务阶段也离散化为T个周期。

首先在预订周期，由于预订顾客的停车时长可能不同，将顾客开始停车的周期i和结束停车的周期j视为一个产品(i,j)。用X=(x11,x12,…,x1T,xTT)表示预订状态，其中xij表示已接受的产品(i,j)的预订数量。每接受一个产品(i,j)的预订，平台将获取净收益fij。用pijt表示需求为(i,j)的顾客在预订周期t出现的概率，Vt(X)表示从预订周期到服务周期结束的期望总收益，则有以下随机动态规划(Random Dynamic Programming,简称RDP)模型成立:

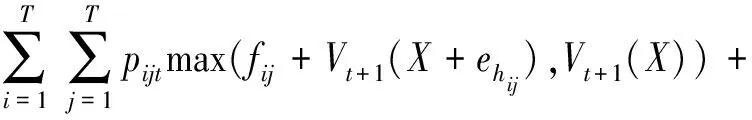
(1)

(2)

(3)

(6)

显然，式(1)的边界条件是Vτ+1(X)=π(X)。其中，式(3)表示服务周期的收益由延时收入与惩罚成本构成；式(4)表示实际接受的预订数量与延时量不超过车位总量；式(5)表示延时需求服从二项分布。

由于式(1)中预订状态的维度较高，很难直接进行求解。实际上，若将每一个服务周期作为一种资源，产品(i,j)需要耗费多种资源，因此该问题属于网络收益管理问题。接下来，我们将分不同情况合理简化网络结构。

2 算法设计

2.1 延时需求可以被拒绝的产品分解算法

(7)

(8)

zij≤wij,i=1,2,…,T-1;j=i,i+1,…,T-1

(9)

wij～b(xij,qij),i=1,2,…,T-1;j=i,i+1,…,T-1

(10)

2.1.1 单产品分解模型(Product-Based Decomposition model,简称:PBD)构建

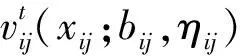
(11)

(12)

(13)

ηij≤bij,i=1,2,…,T;j=i,i+1,…,T

(14)

bij,ηij∈Z+,i=1,2,…,T;j=i,i+1,…,T

(15)

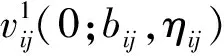
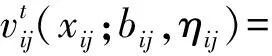
(16)

其中xij≤bij。若延时可以被拒绝，则式(16)的边界条件为:

(17)

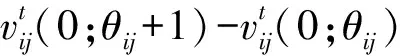
2.1.2 算法设计

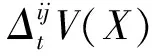
PBD算法:Step1:初始化参数:预订周期和服务周期τ,T,预订到达率pijt,延时概率qij,车位容量Q;Step2:当预订周期的预订状态为x时,若产品(i,j)到达,将式(16),(17)带入表达式(11),求解式(11)～(14),将最优解取整得到b∗ij,η∗ij; Step3:根据式(16),(17),计算vtij(xij;b∗ij,η∗ij)-vtij(xij+1;b∗ij,η∗ij)。当产品(i,j)的预订需求到达时,若fij⩾vtij(xij;b∗ij,η∗ij)-vtij(xij+1;b∗ij,η∗ij),则接受该需求;反之,则拒绝该需求。

2.2 延时需求不能被拒绝的线性规划算法

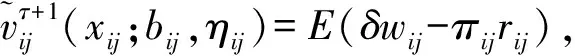
2.2.1 确定性线性规划(Deterministic linear programming,简称DLP)模型构建

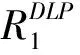
(18)

(21)

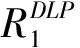
实际中，满足延时需求可能会导致后续到达的预订需求无车位可停，因此假设存在一个容量无限大的虚拟停车场，以存放超过容量的延时需求[20]。第k个服务周期在虚拟停车场停放的车辆数为

用虚拟停车场的车辆数作为衡量拒绝已接受预订产品数量的指标，构建非线性规划(Non-linear programming,简称NLP)模型如下:

式(22)表示平台的收益由平台的预订收入，延时收入以及惩罚成本所构成。

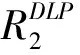
(23)

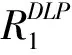
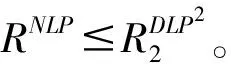
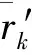
求解DLP2模型得到产品预订量后，根据式(26)～(29)计算可得产品(i,j)的拒绝数量rij，此时若平台已经接受的预订量为X时，平台获得的期望收益可由以下表达式估计得到:

(30)

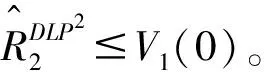
2.2.2 算法设计

为对RDP模型进行求解，通过构建DLP2模型计算当前预订状态下的最优预订量，并采用离散差分的方法计算机会成本，得到预订控制策略。设计算法如下:

DLP2算法Step1:初始化参数:预订周期和服务周期τ,T,预订到达率pijt,延时概率qij,车位容量Q;Step2:当预订周期t的预订状态为X时,若产品(i,j)到达,求解式(21),(24),(31)～(34)得到xij;再根据式(26)～(29)计算得到rij,将X,xij,rij带入(30)式,计算R^DLP22,t+1(X)-R^DLP22,t+1(X+ehij)。Step3:若fij⩾R^DLP22,t+1(X)-R^DLP22,t+1(X+ehij),则接受该需求,更新预订状态X=X+ehij;否则,拒绝该需求,预订状态不变。

3 数值仿真

3.1 算法有效性检验

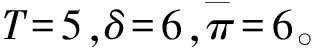
根据图1可得，当车位容量较小时，DLP2算法有效性低于PBD算法，而车位容量较大时，两种算法有效性较好。随着车位数量的增加，当延时概率较小时，DLP2算法获得的收益大于PBD算法获得的收益；反之，PBD算法获得的收益大于DLP2算法获得的收益。实际中，延时收费高于预订收费，顾客会尽可能避免出现延时行为，即延时概率较小。此时，DLP2算法具有有效性。

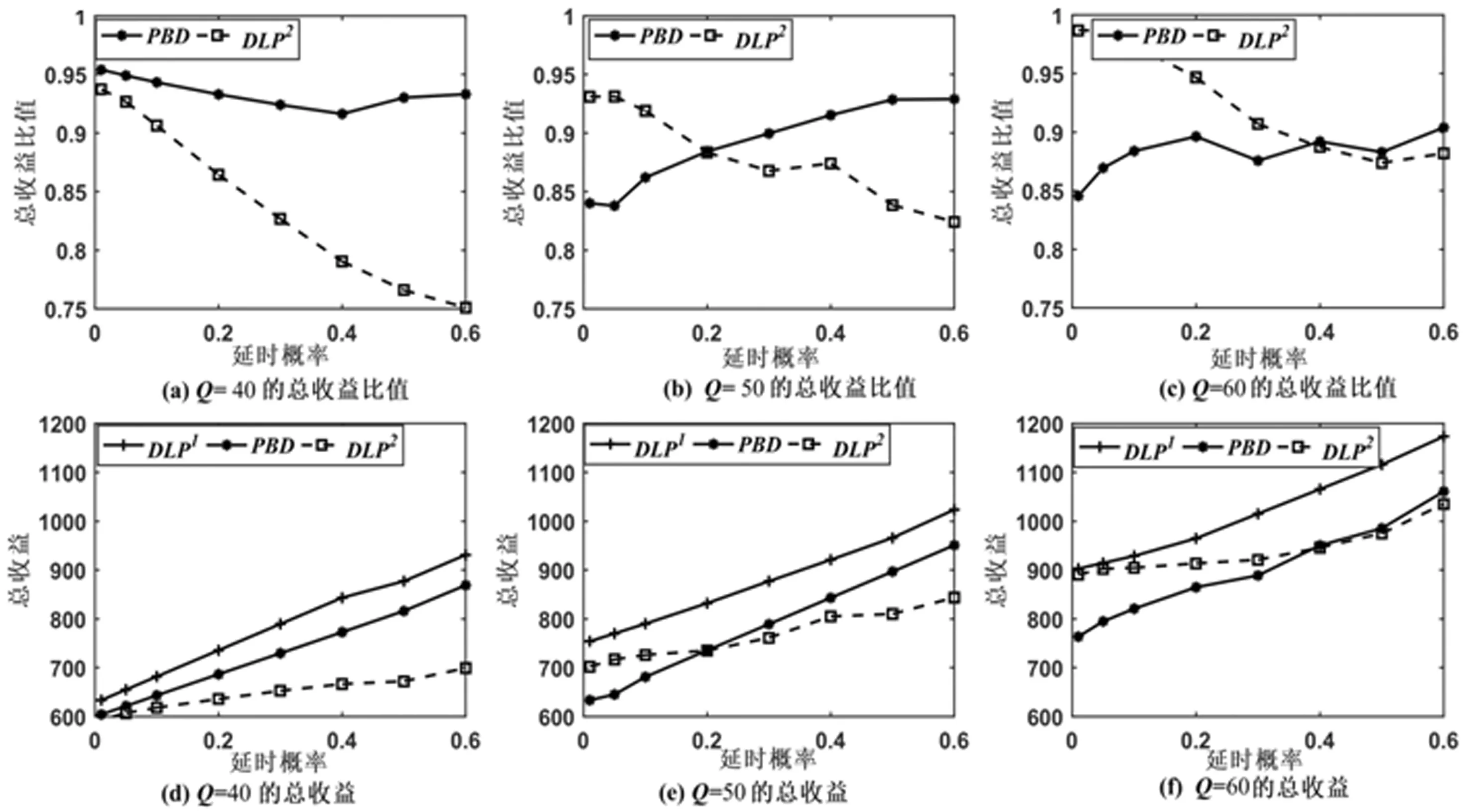
图1 不同延时概率下各算法的有效性

3.2 参数灵敏度分析

3.2.1 机会成本的灵敏度分析

当平台面对预订顾客到达时，决策的关键是对机会成本进行估计。考虑到延时概率将会影响服务周期的产品收益，因此接下来将通过数值仿真验证延时概率对不同算法下的机会成本的影响，具体仿真结果见图2。

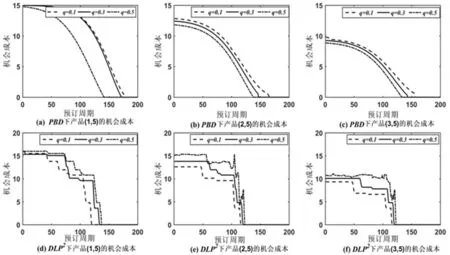
图2 不同延时概率下的机会成本

根据图2可得，机会成本随着预订周期的推移将减少。随着延时概率的增加，DLP2算法拒绝预订的可能性增加，因此机会成本逐渐增加，而在PBD算法中，随着延时概率的增加，需求量增加，机会成本将减少。

3.2.2 预订周期的灵敏度分析

由于预订周期的长短会影响平台的收益，因此，平台需要设置合理的预订周期来接受预订顾客。接下来将分析不同预订周期数对平台收益的影响，具体仿真结果见图3～图4。

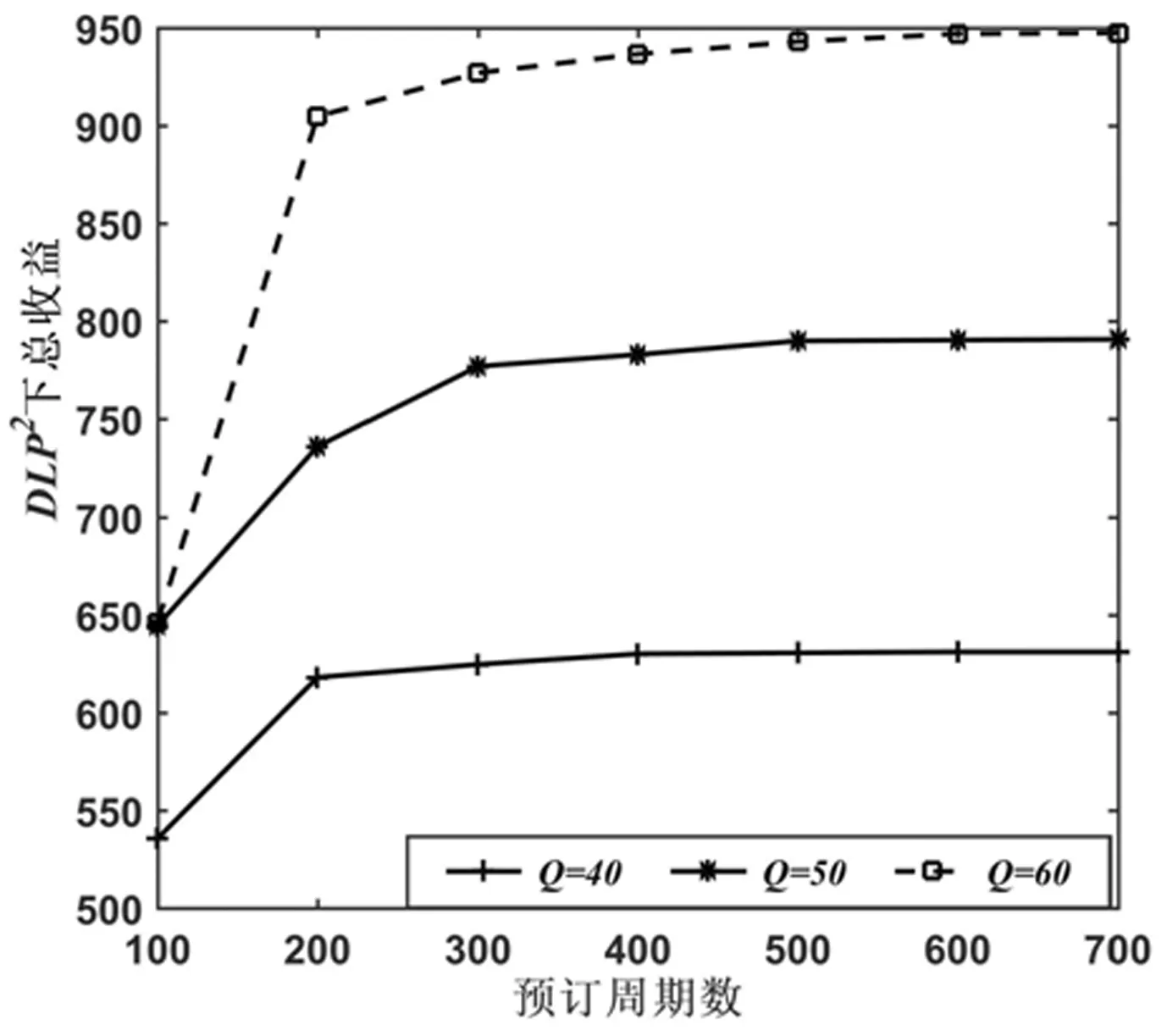
图3 DLP2算法下不同预订周期数的总收益

图4 PBD算法下不同预订周期数的总收益

根据图3～图4得到，随着预订决策周期数的增加，平台的边际收益将先增加后减少。因此，预订周期存在最优值。根据图3，图4还可以得到，车位容量越小，总收益越快达到稳定值，即车位容量与最优预订周期数成正比。

3.2.3 预订价格的灵敏度分析

接下来，我们将研究不同的预订价格下平台的预订控制效果。定义平台的服务率=平台接受的预订总数/预订需求总数，车位的利用率=服务周期接受的车位总数/车位容量。通过对不同的预订价格进行数值仿真，结果如图5所示。

根据图5可得，延时概率增加，平台的车位利用率也会增加。当延时概率较小且预订价格较低时，DLP2算法下的平台服务率和车位利用率均高于PBD算法下的平台服务率和车位利用率，反之，也成立。随着延时概率的增加，DLP2算法下的平台服务率逐渐减小，而PBD算法下的平台服务率却有所上升。

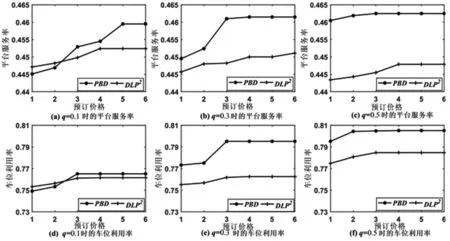
图5 不同预订价格下的平台服务率和车位利用率的变化

4 结论

本文针对车位共享用户可能存在延时行为的问题，构建了预订顾客延时离开的随机动态规划模型。由于随机动态规划模型很难进行求解，因此分别构建了模型的上下界，并基于延时能否被拒绝两种情况设计算法求解平台的预订策略。最后，本文通过大量的数值仿真研究发现：随着预订周期数的增加，总收益将增加，但是当预订周期数增加到一定程度时，总收益将趋于稳定，即预订周期数存在最优值。同时，车位数量越多，则平台设置的预订周期越长，反之，则平台设置的预订周期越短。随着延时概率的增加，若延时可以被拒绝，平台接受预订的可能性将增加；而若延时不可以被拒绝，则平台接受预订的可能性将减小。虽然随着延时概率的增加，DLP2算法下的平台服务率下降，但是在服务周期，延时概率增加，则延时需求增加，因此不论延时需求是否可以被拒绝，延时概率增加均会提高车位的利用率，从而提高平台的收益。当延时概率较大或者车位容量较小时，PBD算法下获得的收益高于DLP2算法所获得的收益，此时，平台需激励顾客提前提供延时信息以进行决策；反之，平台可以采用DLP2算法进行预订控制决策。本文为共享车位的预订分配提供了理论支持和实践指导，具有一定的现实意义。