考虑顾客退货和固定成本的联合补货与定价策略
2022-07-15刘志学
赵 玲, 刘志学
(1.佛山科学技术学院 经济管理学院,广东 佛山 528000; 2.华中科技大学 管理学院,湖北 武汉 430074)
0 引言
随着电子商务的快速发展,企业越来越重视服务质量。因此,大多数电子商务零售商推出“七天无理由退货”服务和上门取件服务。这使得顾客退货更为经济方便,进而导致更多顾客退货。例如,新浪财经报道,2013年电子商务零售商“天猫”的服饰类商品中,运动鞋和运动服等30天平均退货率高达15.07%[1];来自零售分析公司Appriss Retail的数据表明,2019年美国零售行业因网络退货造成的损失超过200亿美元[2]。较高的退货率加重了电子商务零售商的运营成本负担,若处理不好,则会导致严重亏损。因此,有必要考虑退货对企业运营决策的影响。
电子商务零售商在处理下游顾客退货问题的同时,也需要通过从上游供应商订购或直接生产等方式定期补充库存以满足顾客需求。在补货时,不仅会产生与补货量呈线性关系的变动成本,而且也会产生与补货量无关的固定成本。例如,当零售商订购重量较大的产品时,需要给搬运人员提供一定的劳务费用,从而产生固定补货成本。再如,对于自产自销的电子商务零售商而言,在需求高峰期需要大量生产,从而需要招聘临时劳动力并进行培训,而培训劳动力产生的成本与生产量无关,可看作固定成本。更多有关固定成本的例子,参见Chao和Zipkin[3]。
基于以上讨论,电子商务零售商在日常运营管理中,同时面对顾客退货和固定补货成本的现象很常见。然而,在已有的大多数研究中,有的仅考虑固定补货成本,如Chen等[4]等;另一些仅考虑顾客退货,如刘咏梅等[5]以及Chen和Bell[6]等。很少有研究同时考虑顾客退货和固定成本的影响。基于此,本文将在同时考虑顾客退货和固定补货成本的情形下,探究电子商务零售商利润最大化的补货和定价联合策略。具体地,考虑允许顾客免费退货情形,零售商的补货成本包括固定和线性变动成本,而且面对的顾客需求随机且依赖定价。零售商的目标是通过同时决策每周期商品的补货水平和定价,从而最大化有限计划期内的总利润。本论文首先刻画最优策略,然后根据策略特征提出启发式求解策略。最后,利用数值算例验证启发式策略的近似最优性,并探讨退货率和固定成本的影响。
1 文献综述
在与顾客退货相关的研究中,大多数考虑的是单期或两期问题,如Granot和Yin[7],李建斌和李赟[8]以及卢美丽等[9]等。很少有研究考虑多期情形下的顾客退货问题。Chen和Bell[6]分别在需求为确定性和随机性两种情形下讨论了多周期的库存与定价问题,其中在随机情形中假设需求函数是加法结构,而且需求分布满足一定条件;通过对目标函数求一阶导的方法,他们得出最优定价和库存与成本参数及退货参数之间的关系。张霖霖和姚忠[10]也采用导数分析法分别讨论类似确定性和随机性模型,但需求函数是乘法结构。应该指出的是,文献[6]和[10]都忽略了固定成本。然而,电子商务零售商在实际中会因搬运费用等问题产生固定成本,这促使本文探讨同时考虑固定成本和顾客退货的随机动态补货模型。固定成本的引入使得本研究的模型不再具有可微性,导致导数方法不再适用本文的分析。因此,本文成果拓展了类似研究问题的结论。
与本文模型相关的另一个文献流是考虑固定补货成本的多周期联合库存与定价问题。在延期交货情形下,Chen和Simchi-levi[11],Chen等[4]和Hu等[12]分别对固定与线性补货成本、分段线性凹补货成本和分段线性凸/凹补货成本的随机动态规划模型进行探讨。这些模型中延期交货的假设使得类似凹性(如K-凹性[11],拟-K-凹性[4]和κ-凹性[12]等)在最优化问题中成立,从而可以应用这些性质刻画最优策略。对于缺货不补情形,Chen等[13]在假设需求函数为加法结构且随机变量分布满足一定条件的情形下,证明(s,S,p)策略最优。Song等[14]则在乘法需求结构下证明最优策略为(s,S,A,p)策略。与(s,S,p)策略相比,(s,S,A,p)策略在区间A上的决策要根据实际情况确定。对于比较一般的需求函数结构,Huh和Janakiraman[15]给出(s,S)库存策略最优的充分条件。上述研究中讨论的系统动态都可以写成关于库存y与需求D(p,ε)之差ψ(y-D)(p,ε)的函数形式,其中总需求D(p,ε)依赖定价p与随机变量ε。然而,由于顾客退货因素的引入,ψ(y-D(p,ε))结构对于本文更加复杂的系统动态不再成立,这给本文的分析带来了挑战。针对此,本研究通过分析最优值函数的结构部分刻画最优策略,并根据刻画提出近似最优的启发式算法。此外,上述讨论缺货不补情形的研究中,文献[13]和[14]都对需求密度函数施加了假设,文献[15]给出的最优策略的充分条件通常难以直接判断;而本文讨论的一般需求情形则不需要判断充分条件。
综上所述,一方面,目前关于顾客退货的研究大多考虑的是单期或两期问题,而少有的几篇有关多期问题的文献讨论的补货成本仅为线性结构,忽略了固定成本。然而,零售商会由于支付运费等原因产生固定成本,因而同时考虑顾客退货和固定成本的库存定价问题非常值得研究。另一方面,在有关考虑固定补货成本的多周期联合库存与定价模型中鲜有考虑顾客退货情形,同时顾客退货因素的引入又会导致系统动态的复杂性从而增加分析的难度。因此,本文在现有研究的基础上,建立同时考虑顾客退货和固定成本的动态库存与定价模型,通过分析最优值函数的性质刻画最优策略,并探讨退货率和固定成本对最优策略的影响。
2 模型建立
电子商务零售商的目标是最大化其在有限计划期(包含T个周期)内的总期望折扣利润。在每周期开始时,电子商务零售商都需要根据初始库存决策商品的定价和补货量,然后用已有的库存满足需求,并允许免费退货,接下来收到退货并进行处理,最后该周期的利润产生,下一周期的初始库存生成。假设每周期的需求随机且依赖定价,而且对于任意的t=1,2,…,T,第t周期的需求函数可以写成加法或乘法形式,即
D(p,εt)=d(p)+εt,D(p,εt)=d(p)εt
(1)
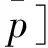
第t周期的成本包括补货、库存和退货成本,记其固定补货成本为K(≥0),单位变动补货成本为c。那么当该零售商补货z单位时,需要支付补货成本c(z)=Kδ(z)+cz,其中指标函数δ(·)满足:如果z=0那么δ(z)=0;否则δ(z)=1。假设当电子商务零售商补货后的库存水平y高于(低于)顾客需求D(p,εt)时会产生库存持有(短缺)成本,则库存成本为
h[y-D(p,εt)]++b[D(p,εt)-y]+
(2)
其中非负参数h和b分别为单位库存持有成本和单位缺货惩罚成本,x+表示x与0的最大值,即x+=max{x,0}。为了提高服务质量,在不影响产品二次销售的情形下,电子商务零售商允许顾客在一个周期内进行退货。因为销售量越多,退货量越大,所以假设退货量与满足的顾客需求成正比。该假设很常见,如张霖霖和姚忠[10]等。为简便,记x∧y=min{x,y},那么退货量为η[D(p,εt)∧y],其中η∈[0,1)和D(p,εt)∧y分别为退货率和满足的顾客需求。假设退货的顾客可得到全价赔偿,每件退货因为重新包装、运费等因素给电子商务零售商带来的损失为L(≤c),而且退回的货物可在当期到达零售商。那么,在第t周期电子商务零售商因提供退货服务而退给顾客的费用和造成的损失分别为pη[D(p,εt)∧y]与Lη[D(p,εt)∧y],所以因顾客退货产生的成本为η(L+p)[D(p,εt)∧y]。
假设当电子商务零售商的库存水平高于顾客需求时,剩余库存可以留在后续周期继续使用;否则,未满足的需求不再满足。那么,给定补货后的库存水平y,第t周期结束时电子商务零售商的库存为
φ(y,p,εt)=[y-D(p,εt)]++η[D(p,εt)∧y]
(3)
其中[y-D(p,εt)]+为第t周期满足需求之后剩余的库存,η[D(p,εt)∧y]是退货量。
令γ∈[0,1]为折扣因子,E为对εt求期望的符号,Ft(x)为第t周期的预期折扣利润关于初始库存x≥0的函数,FT+1(x)=cx。那么相应的动态规划问题如下:

[Kδ(y-x)+c(y-x)]-
E[h(y-D)(p,εt))++
b(D(p,εt)-y)+]-
η(L+p)E[D(p,εt)∧y]+
γEFt+1(φ(y,p,εt))}
(4)
其中目标函数中的前四项分别为第t周期的期望收益、补货成本、期望库存成本和期望退货成本。为简便,定义函数ft(x)=Ft(x)-cx和
Gt(y,p)=(p-ηL-ηp)E[D,(p,εt)∧y]-
hE[y-D(p,εt)]+-bE[D(p,εt)-y]+-
cy+γcEφ(y,p,εt)
(5)
于是,上述动态规划问题等价于:
其中

(7)
而且fT+1(x)≡0。给定x,记问题(6)在第t周期的最优解为yt(x);给定y,记问题(7)的最优解为Pt(y)。那么,最优定价与初始库存x的关系pt(x)=Pt(yt(x))。为便于刻画最优解,下面定义St为gt(y)在区间[0,+∞)上最小的最大值点,st为满足不等式gt(y)>gt(St)-K且不大于St的下确界,即
(8)
注意到εt是连续型随机变量,而且式(7)的目标函数函数是对εt求期望后得到,因而该目标函数连续,进而得到式(7)的最优值函数gt(y)也连续,这可确保上述两个界值的存在性。
3 最优策略的刻画
本节首先针对一般需求分布情形,在乘法和加法结构需求前提下部分刻画最优策略。然后,针对特殊需求分布情形,在乘法结构需求前提下更严格地刻画最优策略;而对于加法结构需求,由于技术限制故将其作为后续研究问题。注意这里提到的特殊需求分布指随机变量εt的失效率函数r(u)=uw(u)/[1-W(u)]递增的分布(详见3.2节假设),而一般需求分布则包括任何类型的分布。此外,两种需求函数结构的不同在于定价影响需求随机性的方式不同,其中式(1)表明在加法和乘法结构中定价分别影响需求D(p,εt)分布的位置与形状。
3.1 一般需求分布下的最优策略
在需求服从一般分布的情形下,探讨随机动态规划问题(6)在多期情形下的最优解。固定成本的引入以及系统动态φ(y,p,εt)结构的复杂性使函数gt不具有凹性,为多期情形下最优策略的刻画带来挑战。针对此,本文可用以下结论刻画最优策略。
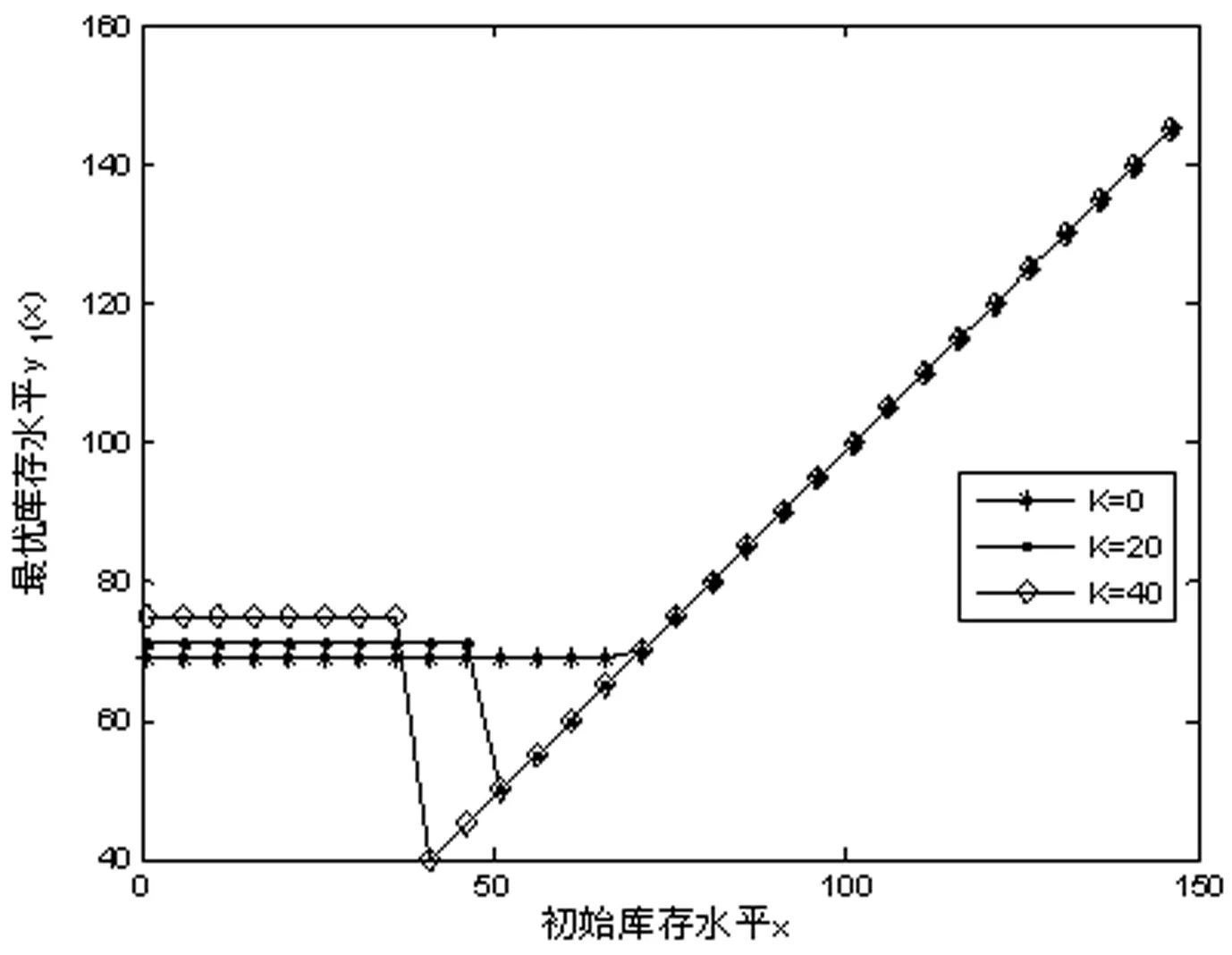
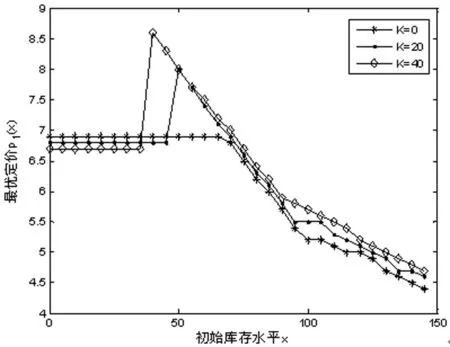
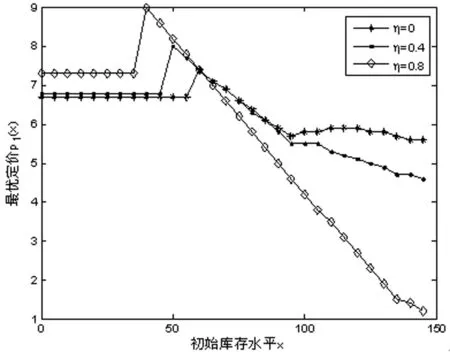
为便于描述,首先引入K-减函数[16]的概念。如果对于任意的x It(y,p,q)=-(ap+l1)E[D(q,εt)-y]+ -l2E[y-D(q,εt)]+ (9) (10) 命题1对任意周期t,当y≥Mt时,gt(y)是严格K-减函数。从命题1可以看出,当y≥Mt时,gt(y)是严格K-减。也就是说,对于任意y>x≥Mt,有gt(x)>gt(y)-K。注意到gt(x)为第t周期不补货情形下第t周期到最后一周期的总利润,gt(y)-K为第t周期补货至y的情形下第t周期到最后一周期的总利润。因此,当初始库存水平x≥Mt时,不补货比补货至任意库存水平得到的利润更高。应用这个结论,可刻画多期问题的最优策略。 定理1对于任意t,当x≤st时yt(x)=St;当x≥Mt时yt(x)=x,其中st≤Mt。 由定理1可知,当电子商务零售商的初始库存水平x低于界值st时,需要将库存水平增加至St;当初始库存水平x高于Mt时,不需要补充库存。不等式关系st≤Mt将为下文启发式算法的提出提供理论依据。 考虑到在一般需求分布情形下,定理1并没有完全刻画多期问题的最优策略。因此,本小节将在特殊需求分布情形下更为具体地刻画最优策略。特别地,此处主要考虑乘法结构的需求函数即D(p,εt)=d(p)εt,以及稳定的系统,即εt关于周期t独立而且具有相同的分布。因此,可以省去εt,μt和Gt的下标,简写为ε,μ和G。有关随机变量ε分布和成本参数的假设如下: 假设1随机变量ε的失效率函数r(u)=uw(u)/[1-W(u)]递增。 假设2单位缺货惩罚成本b=0。 由假设1可知,虽然的分布有限制,但包括大多数常用分布,如均匀分布、正态分布以及指数分布等[17]。假设2表明未满足的顾客需求不会给零售商带来损失,Song等[14]也考虑了这个假设。 定理2在第t=T周期,当x≤st时,yt(x)=St;当x>st时,yt(x)=x。 由定理2可知,在单期情形下,当电子商务零售商的初始库存x低于库存点st时,需要补货至St;否则不补货最优。也就是说,在单期情形下最优联合补货与定价策略是(s,S,p)策略。 命题3如果条件1成立而且Q(y)是拟凹函数,那么对于任意的y2>y1≥S或y2 由命题3可知,当条件1满足且Q(y)是拟凹函数时,g(t)y是K-减。命题3与Huh和Janakiraman[15]中命题2的结论相似,但这里讨论的最优化问题的系统动态φ(y,p,ε)的形式更为一般化,不仅包含Huh和Janakiraman中不考虑顾客退货情形即ψ(y-D(p,ε)),而且包含顾客退货情形即[y-D(p,ε)]++η[D(p,ε)∧y]。 应用命题2和3中函数G(y,p)及gt(y)的性质,下面将刻画多期问题的最优解。 定理3如果假设1和2成立,那么最优补货水平 (11) 而且,当K=0时有st=S,所以若x 由定理3可知,当初始库存x低于界值st时,补充库存至St最优;当x≥S时,不补充库存最优;当st≤x 首先根据最优策略的结构化性质为最优化问题构造启发式算法并检验其近似最优性,然后探讨固定补货成本和退货率对最优库存水平和定价水平的影响。 注意到固定成本的引入以及系统动态结构的复杂性导致定理1和3没有完全刻画多期问题的最优策略。因此,将根据已有刻画为最优化问题构造启发式策略。 (i)计算函数 本小节探讨固定补货成本K和顾客的退货率η对补货决策和定价决策产生的影响。在下面所有数值例子中,设置成本参数为c=1,b=3,h=2,L=0.5。确定性需求与定价的关系为d(p)=10-p,p∈[1,10],而且εt在集合{0,1,2,…,50}上均匀分布,设置总周期数T=3,折扣因子γ=0.9。 图1和2分别是退货率η=0.4时不同固定成本情形下补货决策与定价决策随初始库存水平的变化。由图1可知,随着固定成本的增大,区分电子商务零售商是否需要补货的界值减小,最优库存水平增大。这说明固定成本越大,电子商务零售商补货的可能性越小。此外,图1还表明,对于给定的K,总存在一个界值,当初始库存水平低于这个界值时,电子商务零售商需补货至一个固定的水平,否则不需要补货。这与定理1中对最优策略结构的刻画以及算法1中启发式策略的结构一致。从图2可以看出,当初始库存水平较低时,最优价格不变,而且该最优价格随着固定成本呈递减变化;当初始库存水平较高时,电子商务零售商的最优定价随着固定成本的增加而增加。这意味着当电子商务零售商的初始库存较少时,随着固定成本的升高,需要通过降低销售价格生成更多的需求,从而增大利润。此外,图2还表明,对于给定的固定成本K,当初始库存较低时,电子商务零售商的最优定价维持不变;否则最优定价随初始库存递减。也就意味着当电子商务零售商的库存较多时,需要通过降低定价增大顾客的需求从而减少库存持有成本,以增加利润。 图3和4分别是固定成本K=20时不同退货率情形下的最优库存水平与最优定价。从图3可以看出,随着退货率的增加,用于区分是否需要补货的界值减小,最优库存水平也减小。这意味着当退货率较大时,电子商务零售商补充库存的可能性减少。由图4可知,当初始库存水平较低(高)时,电子商务零售商的最优定价随退货率的增加而增加(降低),意味着当初始库存水平较低时,电子商务零售商所得的边际利润随退货率递减,因而需要通过提高定价来相应地增加边际利润;当初始库存水平较高时,随着退货率的增加,电子商务零售商需要通过降低定价来增加需求,从而增加利润。 在考虑顾客退货和固定补货成本的情形下,本论文专题探讨了电子商务零售商面对的多周期联合库存与定价问题。针对一般需求分布和一般需求函数结构,部分刻画多期问题的最优策略;针对特殊需求分布以及乘法结构的需求函数,证明单期问题的最优策略为(s,S,p)策略,并对多期问题的最优策略进行严格刻画。在此基础上构造启发式策略,并通过数值模拟验证启发式策略的近似最优性,检验了固定成本和顾客退货率的影响。本研究的管理启示主要有两点:①如果电子商务零售商当前库存较少,那么当固定成本(退货率)增大时,电子商务零售商会在增加(降低)补货水平的同时降低(提高)定价;②如果电子商务零售商当前库存较多,那么电子商务零售商不用补货,当固定成本(退货率)增大时,电子商务零售商应该提高(降低)价格。这些研究成果将为电子商务零售商灵活应对补货成本结构的复杂性和顾客退货现象提供有效指导。 图1 固定成本对最优库存水平的影响 图2 固定成本对最优定价的影响 图3 退货率对最优库存水平的影响 图4 退货率对最优定价的影响


3.2 特殊需求分布下的最优策略
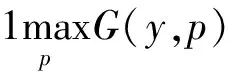



4 启发式算法及数值分析
4.1 启发式策略的构造及其检验

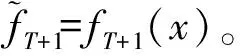

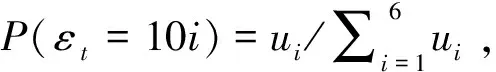
4.2 固定成本和退货率的影响
5 结论