飞行速度可调导弹的自适应滑模制导律

花文华, 张金鹏,2

(1.中国空空导弹研究院，河南 洛阳 471000； 2.航空制导武器航空科技重点实验室，河南 洛阳 471000)

0 引言

导弹的飞行速度和弹道的转弯半径、过载等紧密相关，在飞行过程中的速度变化会通过剩余飞行时间、前置角等产生额外的视线角速度，从而增加对过载的需求，甚至影响制导性能[1]。本文主要针对一类加装有推力可调发动机的导弹开展制导律的研究，这样一类发动机包括冲压发动机和涡喷发动机等。对于采用固体或液体火箭发动机的导弹，飞行速度是不可控的，一般在制导律的设计中考虑速度变化带来的影响，而非进行速度的直接控制。采用推力可调发动机的导弹在轴向多了一个控制自由度。通过轴向飞行速度控制来保持导弹飞行速度的稳定将有助于缓解飞行速度变化带来的影响。产生脱靶量的因素有多种，包括视线角速度、目标横向加速度、目标飞行速度的变化等。如果通过轴向飞行速度控制，向着减少瞬时脱靶量的方向进行加速或速度保持，甚至小推力下借助阻力进行减速，将有助于提升导弹飞行弹道的收敛速度，从而改善制导性能。

将导弹飞行速度变化考虑到制导律的设计当中，这方面的研究文献较多[2-7]，但往往受限于研究对象，并未将导弹速度的变化当作控制量对待。如文献[4]基于微分对策理论，将对策双方的速度变化直接考虑到非线性相对运动关系当中，提出了一种适用于变速拦截情形的有界控制非线性微分对策制导律。文献[7]利用线性化制导回路中解析出的剩余飞行时间内的平均速度预测值，设计了一种考虑导弹速度变化的碰撞时间控制制导律，并将制导律扩展到了适用于非线性系统的情况。

本文主要针对一类飞行速度可调的导弹，开展同时具备速度和脱靶量控制的自适应滑模制导律的研究。首先给出了一种考虑导弹速度变化且以末端过载需求为零的修正比例导引律，在对该制导律瞬时脱靶量部分进一步分析的基础上，采用滑模控制方法进行飞行速度控制律的设计，从而实现导弹横向和速度方向同时在减少脱靶量的方向上控制的目的。

1 问题描述及建模

平面弹目相对运动关系如图1所示。图1中，q为视线角，r为弹目相对距离，a，v，γ分别为加速度、速度和航向角，下标m和t分别对应导弹和目标的状态。本文中变量均为标量。

图1 平面弹目相对运动关系Fig.1 Planar engagement geometry

建立平面弹目相对运动的微分方程，即

(1)

式(1)中，假设导弹和目标具有一阶控制系统动态特性，τm和τt分别为相应的时间常数，umc和utc分别为导弹和目标的控制指令。

可控流量的发动机，如冲压发动机、涡喷发动机等模型复杂，都涉及到对大气模型、进气道、燃烧室和尾喷管等的建模。从制导控制的角度上只需了解发动机的推力，发动机流量的控制则表现为推力的可控，进而实现导弹飞行速度的可控。为了避免对导弹发动机的复杂建模，仅考虑从速度大小控制的角度进行制导律的研究，相应的发动机工作模式简化为轴向加速度大小的调节，这种方法从发动机的内部控制和全弹控制能量优化的角度并不是最优的，但适当的简化，特别是将发动机当作“黑盒”来对待，却可以简化制导控制方法的设计。导弹的飞行速度可控，则可建模为

(2)

式中，amx表示用于飞行速度大小控制的加速度量，假设其具有时间常数为τmx的一阶控制系统动态特性，相应的控制量为umxc。受限于发动机的推力特性和空气阻力，amx总是有界的。

2 制导律推导

2.1 修正的比例导引

比例导引是应用最广泛的制导律形式，在接近速度为负的情况下，总是控制导弹向着视线角速度降低的方向运动，力图构建导弹-目标-命中点的碰撞三角形，实现对目标的毁伤。本文以式(3)形式的比例导引为基础进行制导律的进一步设计，即

(3)

N=Kvmcos(γm-q)

(4)

比例导引具有广泛的衍生形式，典型形式包括扩展比例导引、最优制导律和微分对策制导律[4,8-9]。这些典型形式都包括一个比例导引部分或与视线角速度相关的部分，而由于考虑了目标的机动，导弹和目标的控制系统动态特性等，具有了不同的瞬时脱靶量组成形式。一般都可以写成

(5)

由式(1)可得[10]

(6)

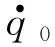
为了改善弹道特性，减少需用过载，改变需用过载的分布，可通过增加修正项的形式对比例导引律进行修正。取修正比例导引律的控制形式为

(7)

式中，变量x表示比例导引律的修正项。

考虑修正项x的影响，由式(1)和式(6)，并取t=tf，可得

(8)

修正项x的设计目的为命中时刻的过载为零，则由式(1)中第4式并经进一步推导，可以得到

(9)

则式(7)可以进一步改写为

(10)

结合式(5)，修正后的比例导引对应的瞬时脱靶量为

(11)

2.2 速度控制的自适应滑模制导律

本文在式(11)的基础上，进一步利用自适应滑模控制方法[11-13]，进行导弹速度控制指令umxc的设计。所定义的滑模面s为

(12)

对s进行求导，并进一步整理，可以得到

(13)

式中

(14)

(15)

(16)

(17)

(18)

假设与目标相关的不确定项Δ是有界的，|Δ|≤ν，其中ν为边界值。

(19)

(20)

(21)

相应的自适应律为

(22)

定义Lyapunov函数为

(23)

对式(23)两边求导并代入式(6)，经进一步推导后可得

(24)

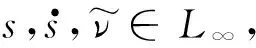
参数κ决定了系统趋近滑模面的速度，选取

(25)

式中，κ4为设计参数。随着弹目相对距离r不断减小，κ逐渐增大，一定程度上可缓解视线角速度发散的影响，并削弱控制上的抖振。

3 仿真及分析

导弹在飞行过程中，会受到空气阻力的影响，如果发动机推力大于阻力，会加速，反之，则会减速。相应地，通过推力的调节可以实现对飞行速度的控制。仿真中对这一过程进行了模拟，假设空气阻力为常值，取为-0.5g。

式(10)所示的修正比例导引律以命中时刻的过载为零为目标，采用mPN(modified PN)表示，涉及的参量η由导弹的轴向加速度amx，以及目标的飞行速度vt、航向角γt及相应的变化率等构成。仿真中，采用对应amx的控制量umx抵消空气阻力带来的速度的下降，保持飞行速度的稳定。假设在闭合mPN计算中涉及的目标参数都是已知的，而ASM在mPN的基础上，不需要知道空气阻力的大小，根据瞬时脱靶量，进行飞行速度的主动控制。

采用所设计的自适应滑模制导律ASM，修正的比例导引律mPN和比例导引PN进行仿真对比和分析。仿真中，取导弹和目标的初值位置分别为(0,0)和(3000,4000)，单位为m，导弹的初速度为300 m/s，初始航向80°，目标的飞行速度取为常值200 m/s，初始航向为135°，并以3g的常值机动进行规避逃逸。导弹的一阶控制系统时间常数和速度控制一阶响应延迟时间常数分别为0.2 s和0.5 s，目标的一阶控制系统时间常数为0.3 s。对于ASM，κ1=2，速度控制的加速度边界值为1g，3种制导律的比例系数K=4，导弹最大加速度6g。仿真结果如图2～7所示。

图2为3种制导律对应的导弹飞行弹道，从图中可以看出PN对应的弹道最为弯曲，mPN和ASM由于采用了导弹飞行速度的控制，弹道则较为平直且较为接近，相应的导弹速度控制的加速度amx和飞行速度vm分别如图3和图4所示。

图2 飞行弹道Fig.2 Flight trajectory

图3 导弹的速度控制量Fig.3 Velocity control value of the missile

图4 导弹的飞行速度Fig.4 Flight velocity of the missile

对于mPN，为保证飞行速度稳定，amx的稳态值与空气阻力的大小相等，vm基本保持不变，而对于ASM，存在一个加速后减速到再次加速的过程，如图3和图4所示，通过该过程，并有效利用空气阻力的影响，ASM对应的弹道曲率是最小的。3种制导律对应的横向加速度和视线角速度分别如图5和图6所示。从图5中可以看出，PN对应的加速度最大，且越接近尾端，受目标机动的影响越大，对过载的需求也越大;而mPN采用了命中时刻的过载为零的修正，全弹道的加速度都较小;ASM在mPN的基础上进行了飞行速度的主动控制，全弹道的加速度同样较小，且小于mPN。在该加速度控制下，PN和mPN的脱靶量分别为0.279 m和0.059 6 m，而ASM的脱靶量趋近于零。图7为ASM对应的滑模面s的变化曲线，受限于速度控制量umxc总是非负的限制，导弹在前端的加速段，s很快收敛到零，而在利用空气阻力的减速过程中，umxc=0，s逐渐偏离零值，在尾端再次进入加速段后，s又收敛到零值附近。

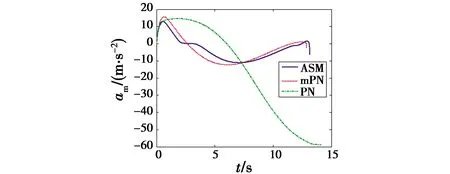
图5 导弹的横向控制量Fig.5 Lateral control value of the missile

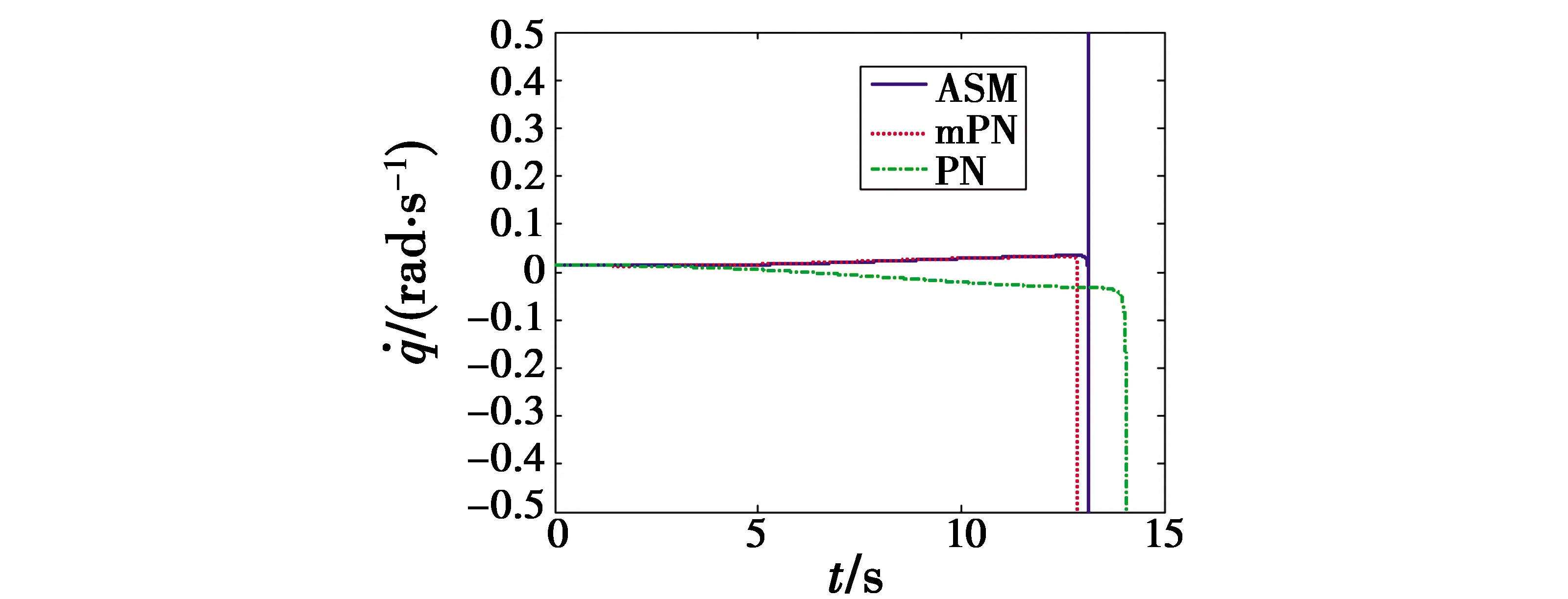
图6 视线角速度Fig.6 Line of sight rate

图7 滑模面Fig.7 Sliding mode surface

4 结论

针对一类飞行速度可控的导弹，利用增加的轴向控制自由度，提出了一种速度可控的自适应滑模制导律。该制导律在末端过载为零的修正比例导引的基础上，通过瞬时脱靶量的分析选取适当的滑模面，并采用自适应滑模控制方法进行设计。仿真结果对比表明，所设计的修正比例导引+飞行速度控制的双重控制自适应滑模制导律可以获得更加平直的弹道，且过载需求更小，自适应滑模制导律达到了假设阻力已知情况下并保持飞行稳定的修正的比例导引的制导性能，且具有一定的优势，同时也说明，对于飞行速度可调的导弹实现飞行速度的稳定也是改善制导性能的有效手段。