轻型仿生机器手的几何求逆优化及轨迹规划

张明松，黄滔

（1. 三峡大学 机械与动力学院，湖北 宜昌 443002；2. 水电机械设备设计与维护湖北省重点实验室，湖北 宜昌 443002）

轻型机械手广泛应用于科研教育以及康复医疗等多个领域，其设计非常轻巧便捷，内置的控制器也比较方便用户轻松控制机械臂，主要是全关节内置的扭矩传感器直接影响到了机械臂的性能[1]，使其拥有良好的安全性及人机交互性[2]。目前国内有很多学者在机械臂运动学上以及机械臂轨迹规划上有比较深入的研究。周霏等[3]基于四自由度机械臂进行运动学仿真，采用数值法进行逆运动学的求解和分析；孙龙等[4]针对目前六自由度机械臂的运动过程中所产生轨迹偏差以及不平稳的问题进行大量模型的仿真研究完成正运动学分析，采用了数值法和多项式插值法，最终确定了机械臂的运动空间的预测和运动轨迹的规划；刘壮壮等[5]针对七自由度冗余机器臂的奇异位型、运动学、动力学以及轨迹规划问题进行详细的说明和分析，利用计算机软件搭建了机械臂仿真环境，并且最终完成了算法的验证和证明；机械臂的运动学分析、轨迹规划、动力学仿真等，其中的各个板块之间都有一定的关联。运动学的理论公式和方程的推导以及最终求解，很大程度上影响了机械臂的运动轨迹规划，机械臂的运动轨迹规划又包含着各个关节的位移、速度、加速度的计算和求解，对于其中的任意值的变化都必定带动整个机械臂运动轨迹的变化，从而会导致之后的动力学仿真分析产生不符合实际的运动。为了保证能够更加符合实际，确保具有实际研究价值，对运动学计算和求解的研究是必不可少的。

本文以KINOVA jaco2 6DOF-S超轻量型机械臂为研究模型，基于一种结合位姿分离思想的几何求逆优化算法完成机械臂的运动分析，并使用数学计算软件进行计算和求解，最终完成对机械手臂的空间运动轨迹的分析，从而证明理论的准确性和研究的合理性。本文中大部分使用数学计算软件完成最终的计算和求解，从而保证求解的准确性。为了保证理论的可靠性和计算的准确性，使用MATLAB中的Robotics仿真模块来建立机械臂数学模型，并将数学模型转换为可直接观察和分析的物理模型，完成对正运动学和改进逆运动学算法进行验证。最后基于正逆运动学的分析和求解，和五次多项式的计算和求解，最终完成对机械手臂进行空间运动轨迹的规划，为机械手臂控制和动力学仿真的研究奠定理论基础。

1 正运动学分析

1.1 连杆坐标系的建立及D-H参数的构建

连杆坐标系的建立是为了研究机器人连杆之间的关系。本文中所研究对象是六自由度冗余机械手臂，因此对应着会有六个关节轴，首先需要确定的是各个相邻的轴线，设关节轴为i（i＝1～6）轴，其相邻关节轴为i＋1轴，具体的坐标系建立步骤如下：

步骤1：确定Zi轴，根据上述所确定的关节轴，可知相邻的两个关节轴分别为i轴和i＋1轴，最终根据两个相邻轴的关系来确定Zi轴，沿关节轴i的指向为Zi轴。

步骤2：确定机械臂空间坐标系的原点位置，确定原点有以下两种方法，第一种方法是关节轴i和i＋1不平行时，此时就需要找出关节轴i和i＋1之间的公垂线，将找出的关节轴i和i＋1的公垂线和关节轴i进行相交，公垂线与关节轴相交的交点就是机械臂中连杆空间坐标系{i}的原点。第二种方法是关节轴i和i＋1平行时，此时就只需找到关节轴i和i＋1的交点，将找到的关节轴i和i＋1的交点和关节轴i相交，关节轴i和i＋1的交点与关节轴相交的交点就是机械臂中连杆空间坐标系{i}的原点。

步骤3：确定六自由度机械臂的Xi轴线。根据步骤1所确定的Zi轴来确定Xi轴，规定Xi轴垂直Zi轴，Xi轴的方向指向Zi＋1。确定Xi轴时也会出现关节轴i和i＋1相交的情况，这种情况下就认为Xi轴与关节轴i和i＋1所在的平面垂直。

步骤4：确定Yi轴。根据步骤1～3可以知道机械臂空间坐标系中的原点、Xi轴、Zi轴，进而可以采用右手定来找出Yi轴。

根据KINOVA jaco2 6DOF-S超轻量型机械臂的结构特点以及上述的坐标系确定方法建立如图1所示的连杆坐标系。

图1 机械臂连杆坐标系

构建D-H参数如表1所示。

表1 Jaco2 6DOF-S超轻量型机械臂D-H参数

1.2 正运动学计算

在定义机械臂的位姿时，其中坐标系{i}和坐标系{i-1}的齐次变换矩阵为，两连杆之间的齐次变换矩阵为[2]：

式中：cθi表示cosθi；sθi表示sinθi；cαi-1表示cosαi-1；sαi-1表示sinαi-1。

已知D-H参数表和齐次变换矩阵，将

参数表中数据代入式（1）可计算出各相邻两个坐标系之间的变换矩阵为：

将矩阵依次相乘可得正运动学公式为：

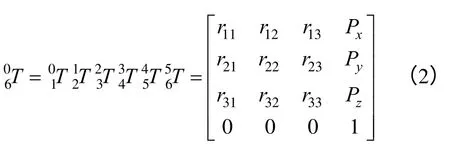
式中：

1.3 正运动学仿真

运用MATLABRobotics Toolbox工具箱中Link函数和SerialLink函数搭建六自由度机械臂模型，生成六自由度机械手臂可视化模型，使用teach 函数生成可调节关节角的人机交互界面，为了能够方便对六自由度机械手臂的研究，笔者将机械手臂的初始姿态设定为各个关节角均为零度时的运动姿态。

如图2所示为机械臂的初始姿态，图2（a）为机械臂关节角控制操作界面，拖动界面上的滑块就可以调节各个关节角度的大小，从而控制六自由度机械臂空间位置的姿态，实现手动控制机械手臂的末端执行器运动到所希望的位姿，图2（b）为六自由度机械手臂的三维模型，此时图中显示的是六自由度机械手臂处于各个关节角为零度时的位姿。右侧图中的机械臂三维模型显示的目的是为了保证手动设置各个关节角时能够实时的观察六自由度机械臂的位姿状态，进而可以更加准确、快速地设定各个关节角度的大小。

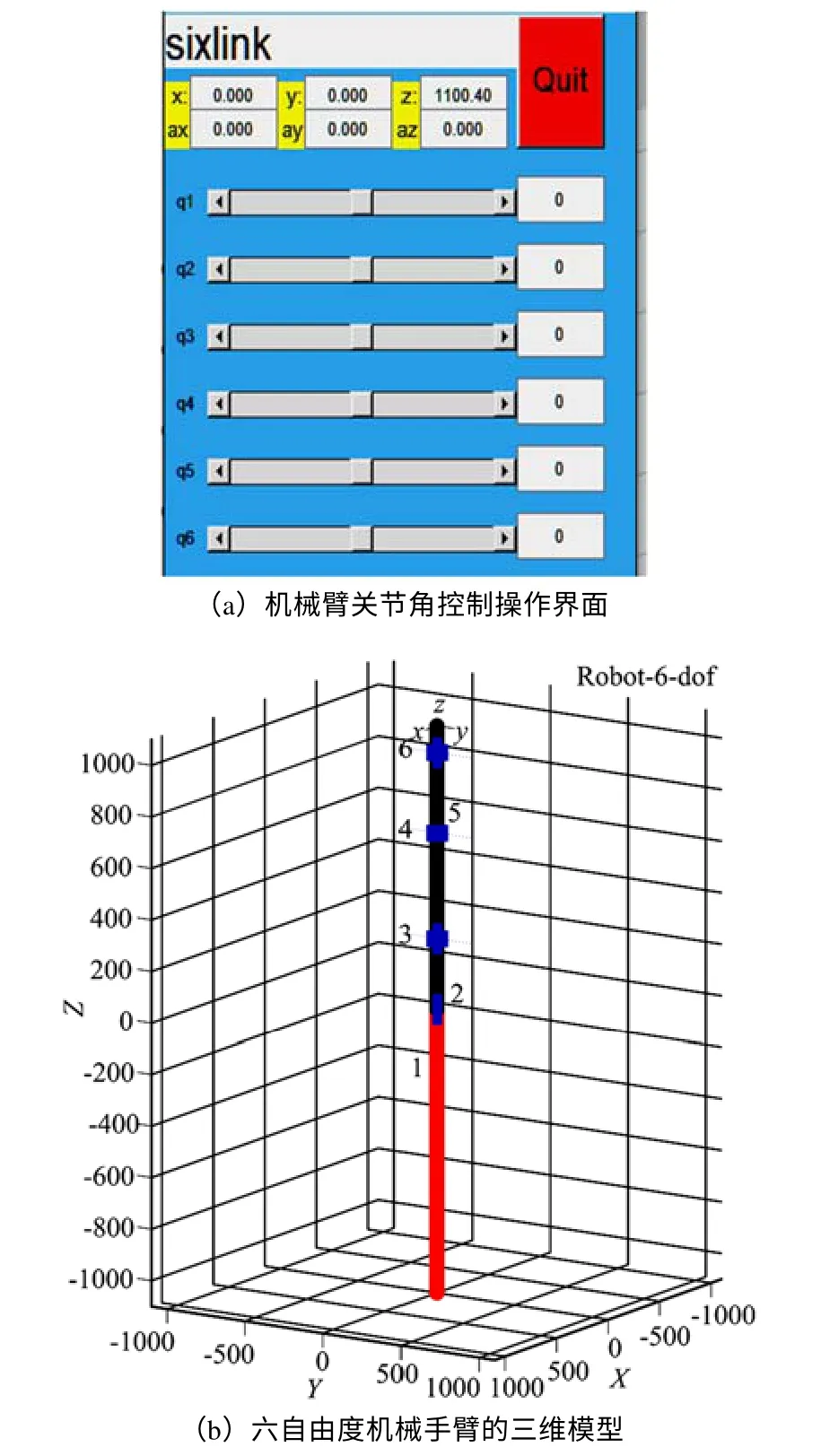
图2 机械臂初始姿态

另外，设置右侧图中的机械臂三维模型也方便了对正运动的计算结果进行验证，本文所采用验证方法的具体步骤为：首先需要依据D-H参数表要求，任意选取六个关节角的角度大小，将其数据代入到本文中所列出的公式中，经过理论计算后会得出一个机械手臂末端执行器的位姿；之后，再通过运用teach()命令进行对比验证，将正运动学所求解的结果代入机器人工具箱中就能够观察机械臂的位置姿态。最后通过比较理论计算后的数值与使用机器人工具箱进行仿真后的数值。本文使用了以上所提到的方法进行了正运动学验算，结果显示两个数值保持一致，说明了本文理论计算是正确的，从而保证了后面的逆运动学和空间轨迹规划的正确性和合理性。

2 几何求逆优化算法的设计

所谓逆运动学其实就是正运动学的逆算过程，在机械手臂实际的工作运行中，往往都是给定机械手臂末端执行器的位置，再通过计算机的运算求解出每个关节角的角度大小，最后传输到各个关节角的控制器中，从而控制着机械手臂实际的运动状态。因此机器臂逆运动学计算就是在已知机械手臂末端执行器的位姿后来进行逆推导过程，通常逆推导后会计算出很多关节角的数值，所以需要根据机械手臂实际的工作要求选取那些符合工作要求的关节角再进行之后的处理。

在逆推导的过程中有很多求解方法，本文采用的是几何解法，将六自由度机械手臂的结构用实线和虚线进行表示，再通过几何学进行求解，但本文中所采用的几何法是基于普通几何法的求解进行优化处理，目的是可以更快的求解结果。本文逆推导的过程为：

式中：R为末端执行器所在坐标系相对基坐标系的旋转矩阵；P为笛卡尔空间中的位置矩阵[6]。

采用旋转矩阵与位置矩阵分离法，使位置矩阵与几何法结合来求解前三个关节角θ1、θ2、θ3随后在此基础上利用关节连杆4、5、6的旋转矩阵来求解余下的关节角[7]。本文为了便于计算，基于θ2＝θ3的前提条件下进行逆运动学求解，具体如下：

（1）步骤1：求关节角θ1、θ2、θ3。

根据D-H坐标系和末端执行器位姿矩阵，可得机械臂末端坐标系原点的位置矩阵[Px Py Pz]T，将机械臂各关节连杆简化为刚体，其几何位置关系如图3所示[8]。

图3 机械臂连杆几何位置关系

由于本文所研究的机械臂关节6的运动对关节5的位置不产生影响。因此可以计算出关节5相对于基坐标的位置矩阵，即：

可得：

由图3可得机械臂末端执行器的位置关系函数表达式为：

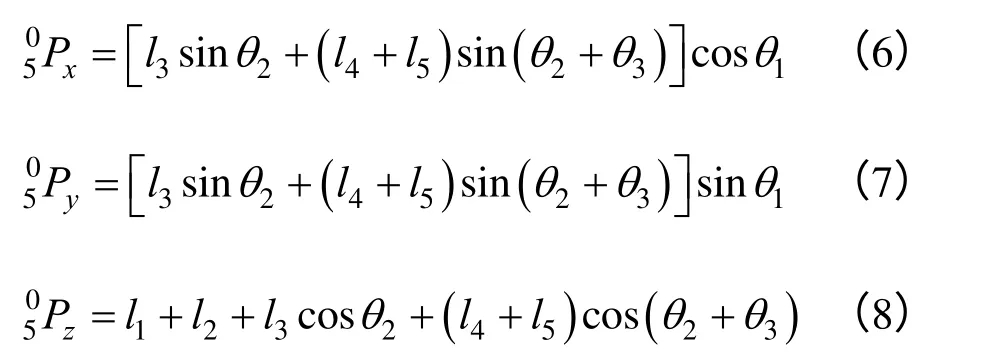
由式（6）、式（7）求解得：

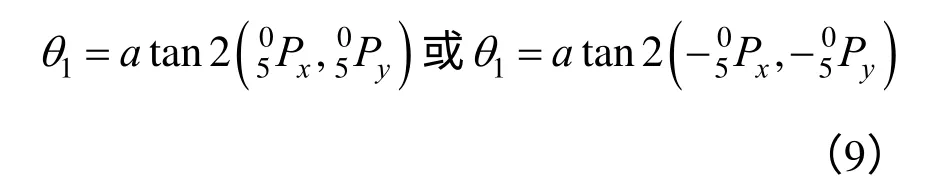
将式（6）和式（8）联立，平方后相加得：

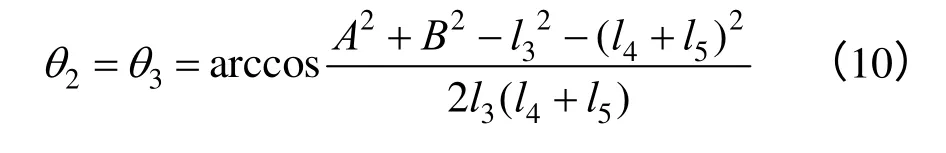
（2）步骤2：求关节角θ4、θ5、θ6。

相邻两连杆间旋转矩阵为：

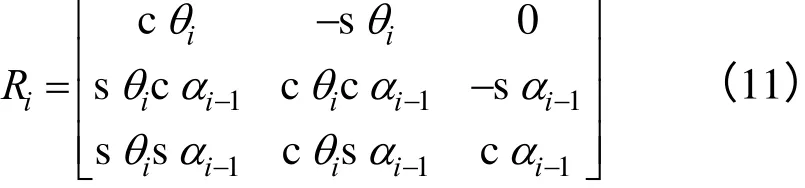
由旋转矩阵正交性质可得：

求解得：

当0＜θ6≤120°时：

当-120°≤θ6≤0时：

由式（15）、式（16）可知θ6有两种解，产生的原因是由于各关节角位移求解结果相互关联。六自由度机械手臂在实际运动过程中会有一部分的解表示的关节角位移是机械手臂到达不了的位置，因此最后所求逆解的选取要由机械手臂的实际工作情况而定[9]。

3 关节空间轨迹规划

关节空间轨迹规划是用来规划机械手臂实际的运动轨迹，主要是利用每个关节的变量与时间之间的函数关系所形成的方程来表述机械手臂的运动轨迹。本文采用的是五次多项式插值算法，基于MatlabRoboticsToolbox平台进行关节空间轨迹规划，进而得到各关节角度、速度和加速度与时间关系曲线[10]。

五次多项式中包含6个待定系数，其中的任意系数都可对起始点和目标点的角度、角速度和角加速度进行同时约束，设六自由度机械手臂关节角符合：

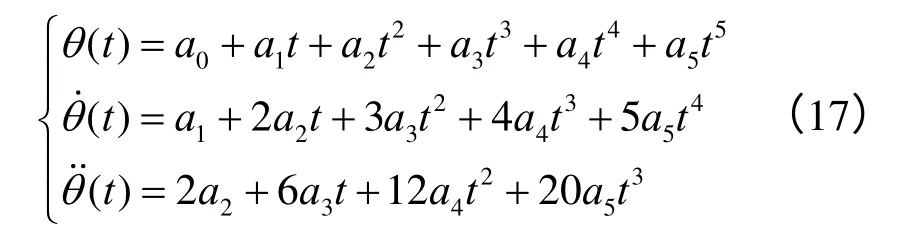
将一小段轨迹的头尾两个点看作运动轨迹的起点θ0和终点θf，并将起始速度约束为V0，终止速度约束为Vf，如下所示：

将约束条件代入函数式（18），可求得式（19），从而可得到插值法规划的轨迹。

就机械手臂的空间轨迹规划问题，通过五次多项式的插值算法，计算出满足多约束条件下六自由度机械手臂运动的多项式方程，并最终通过数学计算工具MATLAB进行运算和仿真得到相应的结果和仿真数据。对六自由度机械手臂进行五次多项式插值，不仅可以得到机械手臂末端执行器的空间轨迹，还可以得到每一个关节的角位移、角速度和角加速度[11]。

如图4所示为机械臂末端关节的空间轨迹图，空间轨迹图的生成需要初始点和终止点两个点作为起始和终止位置，笔者在做起始点和终止点设定时特意选定起始A点为机械臂各关节均为0度时机械臂末端关节的位置，而对空间轨迹终止B点则设定为关节角1为90°、关节角2为负30°、关节角3为30°、关节角4为0°、关节角5为30°、关节角5为0°时的机械臂末端关节位置。图4（a）为机械手臂空间姿态图，图中所显示的是机械手臂移动到B点时的位姿。图4（b）为空间轨迹图，图上所显示的A、B两点分别代表机械手臂的初始点和终止点，空间轨迹线表示的是机械手臂末端关节从初始A点移动到终止B点所经过的路径。从图4来看，空间轨迹为一条曲线型的轨迹，没有突变也没有断口，且机械手臂能准确地到达提前已设置好的的位置，进而说明空间轨迹点设定没有问题并且机械手臂控制具有合理性。

如图5所示为机械手臂各个关节角位移曲线图，从图5中各关节随时间变化的位移曲线图可以看到图中的关节角1、关节角2、关节角3、关节角5的位移曲线随时间变化而变化的大致相同，只是零时刻弧度和达到稳定点时刻不同，而图中的关节角4、关节角6位移显示为零，产生这样的原因是机械手臂的起始点和终止点的设定不同，因此每个关节对应的变化就有所不同。另外，通过对各个关节角的位移曲线图的分析可以说明机械手臂是按照设定的路径和程序进行运动的，进而证明的机械手臂计算和仿真的正确性。

图6、图7分别为六自由度机械手臂的关节角速度曲线图和各关节角加速度曲线图，图中所显示的均是各关节随时间变化而变化的运动情况，关节角1、关节角2、关节角3、关节角5的角速度和角加速度随时间变化的曲线大致相同，且角速度和角加速度均没有突变，各关节角速度和角加速度变化的曲线是连续且缓和。通过图4、图5可知五次多项式机械臂轨迹规划算法的有效性[11]，机械手臂的各关节运动平稳，可达到空间轨迹规划设计要求。

图4 机械臂末端执行器空间轨迹图

图5 各关节角位移曲线图

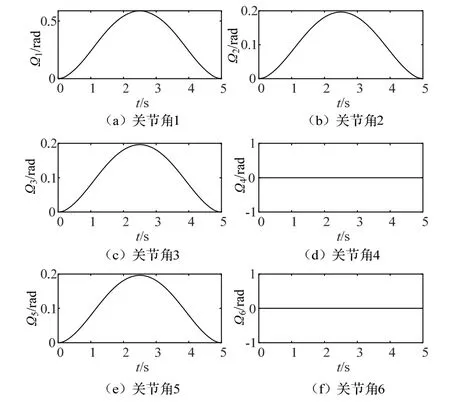
图6 各关节角速度曲线图

图7 各关节角加速度曲线图

4 结论

针对轻型六自由度机械手，本文主要完成了对正逆运动学的推导计算，并就逆推导过程中提出一种结合位姿分离思想的几何求逆优化算法。本文有如下结论：

（1）六自由度机械手臂的正运动学重点在于计算和推导，其求解的结果与逆运动求解是相互关联，并起到验证逆运动结果的作用。

（2）本文中六自由度机械手臂的逆运动学完成了各个关节角的求解，并根据本文所研究的机械手臂的结构要求对几何求逆算法进行了优化处理，提出一种位姿分离的思想，可以更好地解决多自由度求逆困难的问题。

（3）结合D-H坐标系，本文建立了六自由度机械手臂的运动学模型，并推算出了六自由度机械手臂正逆运动学方程的数学函数表达式和各个关节运算求解的过程，然后，通过MATLAB机器人工具箱分别验证和仿真了机械手臂的正、逆运动计算结果以及机械臂关节空间轨迹。本文完成了五次多项式的机械臂轨迹规划并给出了各个关节角的角位移、角速度、角加速度的数据曲线。

本文通过公式推导、方程求解计算、验证仿真，最终结果表明，验算的结果与理论公式计算结果的数值几乎保持一致，证明了本文中KINOVA jaco2 6DOF-S模型结构和计算方法的一致性[7]，对六自由度机械臂空间控制的研究具有很大的借鉴和参考价值，为之后的机械臂动力学等研究提供理论分析和可靠依据[9]。