Risley双棱镜与FSM复合轴实时精密控制技术研究

马秀刚，张文博，陶冶

（四川大学 机械工程学院，四川 成都 610065）

在现代化军事战争中，夺取和保持制空权对战争进程和结局具有决定性影响。为保障战机对空中高速运动目标的快速识别与精准打击能力，光电跟瞄系统需具备极高的跟踪精度与动态响应性能。目前光电跟瞄系统一般采用万向式复合轴结构。其扫描范围大，但响应速度慢、动态性能差，影响跟踪精度[1-2]。然而，由于万向式结构本身限制，跟瞄精度很难再进一步提高，在某些特定场合无法满足光电跟瞄系统的精度要求[3-5]。Risley双棱镜与FSM复合轴结构作为光电跟瞄平台光束指向机构能够有效提高跟瞄系统的跟踪精度与响应速度，因此，在一些对跟瞄精度需求较高且相对视场较小的应用场景有较大的发展潜力。目前，对Risley双棱镜与FSM复合轴跟瞄系统的研究还较少。为了解决Risley双棱镜视场中心出现的盲区问题，彭起等[6-7]提出了一种基于旋转双棱镜的复合轴跟踪系统，解决了Risley双棱镜视野盲区问题。然而，跟瞄系统需要有一定的视场范围，而Risley双棱镜只有在极小范围内才能保证足够的精度，随着扫描范围的增大，光束指向精度会降低[8-11]。

针对以上问题，本文提出一种Risley双棱镜与FSM快反镜复合轴实时精密控制方法。该方法利用Risley双棱镜对动态目标进行捕获与粗级跟踪，神经网络预测模块根据目标与探测器视场中心的偏差（脱靶量）以及目标速度实时预测Risley双棱镜下一个控制周期的误差，再利用FSM直接进行实时补偿，提高系统跟踪精度。本文建立了传统复合轴跟踪平台控制与Risley双棱镜与FSM快反镜复合轴实时精密控制方法的仿真模型，实验结果表明该方法能够有效提高光电跟瞄复合轴系统的响应速度与稳定跟踪精度。

1 Risley双棱镜与FSM复合轴结构与偏差分析

1.1 Risley双棱镜与FSM复合轴跟瞄系统结构分析

光电跟瞄系统一般为两级联动的复合轴系统，复合轴系统一般有单探测器型与双探测器型两种结构。本文选用单探测器型结构作为研究对象，单探测型复合轴结构主轴与子轴共用一个探测器，可消除因装配误差导致的主轴与视轴偏差，同时，结构更简单、紧凑。然而，单探测器系统具有主、子轴耦合更复杂、控制难度更大的特点[12]。本节主要分析Risley双棱镜与FSM复合轴的结构组成与系统光束指向原理。

如图1所示，系统由Risley双棱镜主轴、FSM子轴、成像组、分光镜、激光发射器、CCD探测器以及复合轴控制器组成。两个旋转棱镜共轴排列，目标反射光线穿过Risley双棱镜系统后进入成像组，再经过FSM与分光镜后在CCD探测器上成像。在动态跟踪过程中，假设分光镜不改变透射光束传播方向，Risley双棱镜粗跟踪平台根据探测器提供的脱靶量负责大范围扫描搜索目标并且将其锁定在视场内。FSM系统则通过不断调整位姿，矫正光束指向，提高系统跟瞄精度。由图1可知，目标位置在CCD上成像点与CCD中心偏差越小，激光发射器的瞄准精度越高。因此，无论采用何种结构或者何种控制方法，其最终目的都是减小目标位置与视场中心的偏差以提高战机精准打击能力。本小节主要根据系统结构分析Risley双棱镜系统与FSM系统在进行动态跟瞄过程中的光束指向原理，确定双棱镜旋转角度、FSM旋转角度与光束偏转之间的关系。

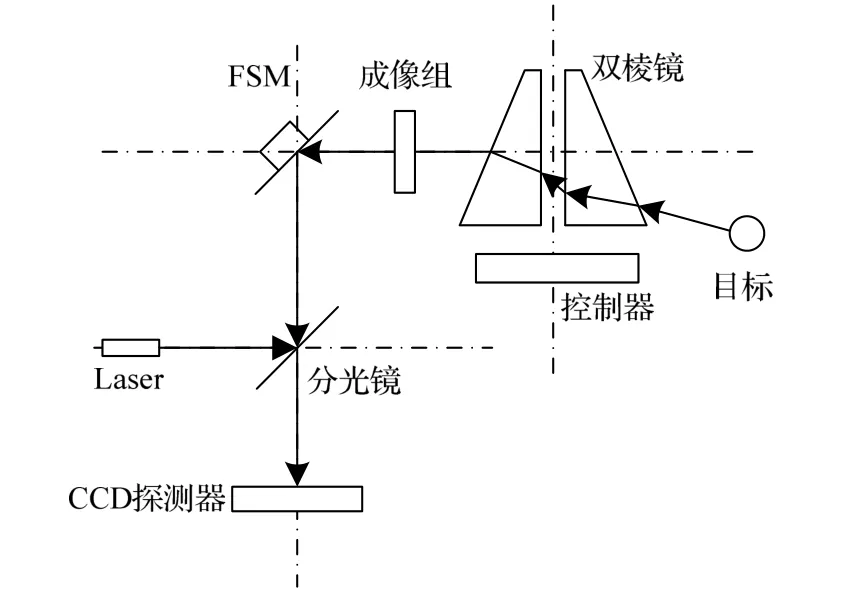
图1 Risley双棱镜与FSM复合轴系统组成

1.1.1 Risley双棱镜光束指向分析

Risley双棱镜作为粗跟踪平台的光束指向机构，一般采用两个具有相同顶角与折射率的棱镜同轴排列而成。Risley双棱镜两个棱镜旋转角度与光束指向之间呈非线性关系，由两个棱镜的旋转角度求解视轴指向（偏转角Φ和方位角Θ）的过程称为正解求解过程，由目标所在方向偏转角Φ和方位角Θ求解两个棱镜的旋转角度的过程称为逆解求解过程。周远等[13-14]对旋转双棱镜的光束指向正解与逆解求解问题进行了详细的研究与验证，通过理论分析分析与实验验证对比了一阶近轴近似方法与非近轴光线追迹法的光束指向与反向解精度，指出通过非近轴光线追迹法求解得出的光束指向精度与反向解更加准确。本文着重研究Risley双棱镜与FSM复合轴跟瞄系统控制方法，需以Risley双棱镜正解与逆解为基础，求解方法则基于文献[13-14]所提方法。

旋转双棱镜光束指向示意图如图2所示跟踪偏差即为视轴指向点与目标所在点的偏差，目标的坐标信息由CCD探测器获取，其偏转角为：

图2 旋转双棱镜光束指向示意图

方位角为：

而视轴指向点的坐标信息需要通过求解视轴光束指向方向的偏转角Φ0与方位角Θ0来计算，可表示为：

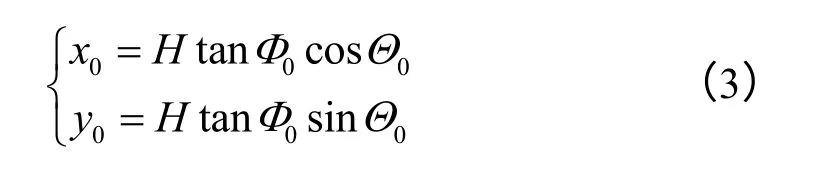
偏转角Φ0与方位角Θ0的表达式为：

式中：（K,L,M）为出射光的方向余弦向量。

对于动态目标跟踪最主要的是跟据目标实际位置计算双棱镜需要旋转得转角，即求旋转双棱镜反向解析解θ1和θ2。一般旋转双棱镜会选用相同材料、相同顶角的棱镜，因此，偏转角Φ0的大小由两棱镜的旋转角差来决定。求两棱镜的转角θ1和θ2可采用两步法，此时有两个组合解[15-16]，当θ1≤θ2时，第一个组合解为当θ1＞θ2时，第二个组合解为

求第二个组合解，假设第一步完成时的方位角表示为，此时同理，第二步两个棱镜同步旋转角度则第二个组合解为：

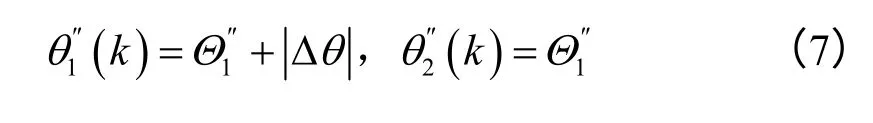
1.1.2 FSM光束指向分析

旋转双棱镜的目标跟踪始终都会存在跟踪残差，使得对目标进行瞄准时激光无法准确指向目标，为了提高激光瞄准精度，引入FSM机构，如图3所示，快反镜初始安装位置为45°角，快反镜绕着自身方位轴与俯仰轴分别旋转α与β，使激光束指向目标。假设此时视轴沿x轴方向，OP与视轴的夹角δ即为跟踪误差，FSM绕着旋转轴A、B分别旋转角α与β，从初始位置П1调整到П2位置，相应的目标在CCD上的成像点由P0移动到O0，即CCD中心。文献[17-18]讨论了出射光与目标方向之间的夹角δ和快反镜旋转角度α、β之间的关系，但其计算过程极为复杂。本文将FSM指向模型简化，在图3中，目标在CCD中偏离中心点O0的大小可用O0M与O0N的值来表示。FSM绕着轴A与轴B旋转可改变O0M与O0N的值，若是FSM安装精度足够，则O0M的大小由FSM绕轴A旋转的角度α决定；O0N的大小则由FSM绕轴B旋转的角度β决定。

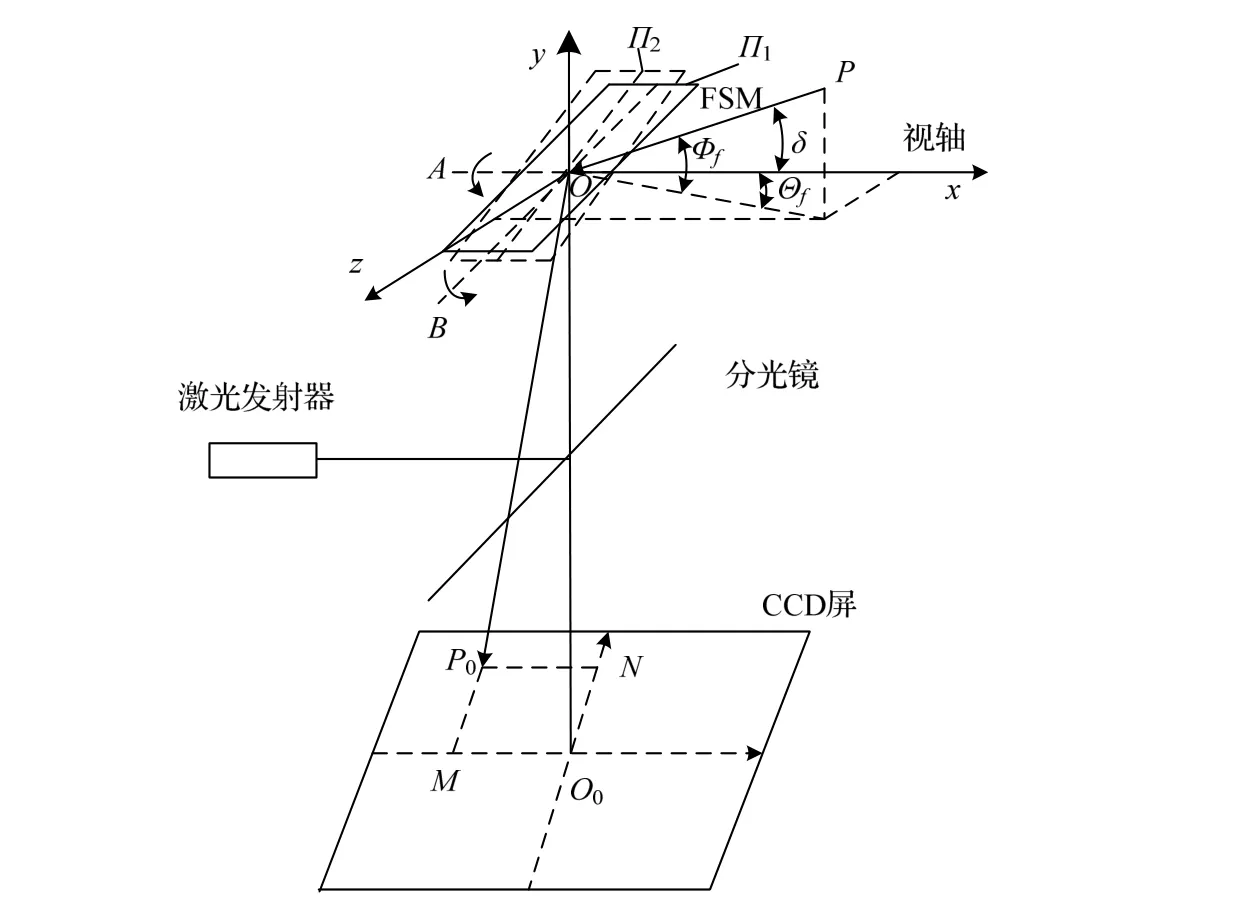
图3 FSM装置光束指向图

FSM绕轴A旋转时光束指向平面示意图如图4所示，为了将目标成像点移动到O0，FSM绕轴A旋转α到达П2，O0M的大小由CCD探测器获取，由图4很容易即可得FSM的旋转角度为：

图4 FSM光束指向平面图

在图4三角形ΔOO0M中，有：

代入式（8）可得：

同理，FSM绕轴B旋转角度为：

1.2 Risley双棱镜与FSM复合轴系统控制方案及偏差分析

Risley双棱镜与FSM复合轴控制系统在跟踪动态目标时，Risley双棱镜主轴系统根据探测器提供的脱靶量驱动两个棱镜旋转实现大范围的目标捕获与一级粗跟踪。FSM子轴系统视场小、精度高、响应速度快，当目标稳定在FSM精跟踪系统视场内，即偏差小于FSM行程时启动，根据神经网络预测模块所预测的主轴偏差预测值进行实时补偿，实现复合轴系统高精度跟踪。然而，由于FSM精跟踪平台行程非常小，要求Risley双棱镜粗跟踪系统偏差在10 mrad以内，否则无法迅速将目标稳定在FSM精跟踪系统视场内。精跟踪系统跟踪精度直接决定了复合轴系统跟踪精度，因此，精跟踪系统需具备微弧度甚至亚微弧度级跟踪精度。

在工程应用中，虽然很多先进控制方法取得了一定的成果，但是在实际应用中实现过程往往非常复杂，难以实现。因此，本文主、子系统采用已经应用成熟且高精度的伺服三环控制+光学闭环反馈控制方案，其框图如图5所示。在进行动态目标跟踪时，通过光学CCD探测器获取目标信息，经过图像处理计算得到目标脱靶量，再通过Risley双棱镜反向解析法求解旋转双棱镜逆解，即两个棱镜目标旋转位置θ1和θ2，并将指令给到伺服驱动器驱动电机快速旋转到指定位置。

图5 Risley双棱镜粗跟踪闭环控制原理图

在保证粗、精跟踪分系统具有足够的精度后，复合轴主、子轴协同控制成为了关键难点。典型的单探测器复合轴粗精控制系统框图如图6所示，D1为CCD探测器，K1为主轴控制器，Gc为主轴执行机构，K2为子轴控制器，Af为子轴执行机构，D2为解耦支路。复合轴系统分为三个工作阶段，第一阶段为目标扫描捕获阶段，该阶段粗跟踪平台按照一定轨迹搜索目标并将其锁定在视场内；第二阶段为粗跟踪阶段，当目标出现在视场内，启动粗跟踪，探测器与Risley双棱镜粗跟踪平台形成闭环系统，控制器K1接收脱靶量并解算得到运动信号驱动Risley双棱镜快速旋转到目标位置，实现粗级跟踪；第三阶段为精跟踪阶段，当目标稳定在FSM精跟踪视场内时，启动精跟踪，FSM系统根据目标脱靶量在其行程内对光束指向进行矫正；同时，Risley双棱镜主轴通过解耦支路对FSM子轴超限量进行修正。然而，这种方法复合轴主轴与子轴运动范围存在矛盾，解耦极为复杂，难以控制，并且补偿量始终落后一个周期，导致跟踪响应速度慢、精度低。

图6 传统单探测器复合轴控制系统控制框图

2 Risley双棱镜与FSM复合轴主轴偏差实时预测与补偿策略

2.1 Risley双棱镜与FSM复合轴系统主轴偏差实时预测

Risley双棱镜粗跟踪系统每一个控制周期的偏差与目标运动速度、加速度以及上一周期偏差等有关，但是难以建立准确的数学模型。RBF 神经网络理论上可以以无限小的精度逼近任意函数，采集多组目标脱靶量、运动速度、目标加速度以及对应的粗跟踪系统偏差作为训练集训练网络，只要训练数据足够多且准确，神经网络就能根据目标运动信息准确预测粗跟踪系统偏差。因此，神经网络模型是Risley双棱镜与FSM复合轴跟瞄系统关键一环，其预测精度决定了复合轴系统的跟踪精度。RBF 神经网络是一种三层前馈网络，分别为输入层、隐含层和输出层，由输入到输出之间是非线性映射关系。由隐含层到输出层之间是线性映射关系，因而极大的加快了网络的学习速度，克服了局部极小问题。RBF神经网络相较于其他神经网络效率较高，并且结构相对简单，只有一个隐含层，学习效率较高。其结构如图7所示[18]。

图7 RBF神经网络结构[19]

在图7的RBF神经网络结构中，n为神经网络输入xn的维数，m为隐含层神经元数，本文以目标脱靶量、目标速度作为网络输入，所以输入层只有两个神经元，隐含层取6个神经元，RBF神经网络的径向基向量设为H＝[h1,h2, …,hm]T，hj为高斯基函数，其表达式为：

式中：Cj＝[cj1,cj2, …,cjm]T为第j个隐含层神经元高斯基函数的中心向量；Bj＝[bj1,bj2,…,bjm]T为第j个隐含层神经元高斯基函数的宽度向量。

高斯基函数宽度bj越大，高斯基函数的非零输出区域越大，即对输入映射能力越强，而中心向量cj则表示此非零输出区域的中心，输入值离中心越近，相应的输出值越大。RBF神经网络输出可表示为：

式中：W＝[w1,w2,…,wm]T，为网络输出层权值矩阵。

RBF神经网络在训练过程中，会不断地调节输出层的权值矩阵W，直到预测精度达到设定值。RBF神经网络可采用梯度下降法来调节权值矩阵，设RBF神经网络的估计误差指标为：

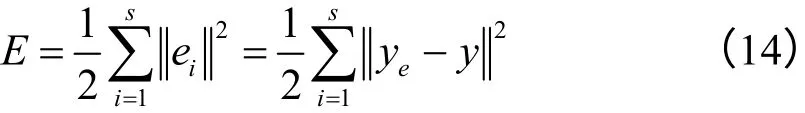
式中：ye为期望输出值；s为输出层神经元个数，本文取s＝1。

根据梯度下降法，网络输出权值、节点中心向量及基函数宽度的迭代算法分别如下：

（1）输出权值向量迭代过程

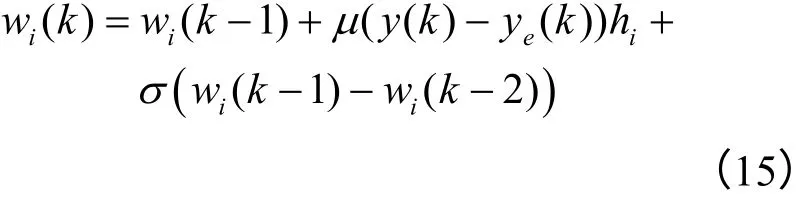
（2）节点中心向量迭代过程

（3）节点基函数宽度向量迭代过程

式中：μ= ∈（ 0,1）为学习速率；σ=∈（ 0,1）为动量因子。

本节介绍并建立了RBF神经网络模型，其作用是预测Risley双棱镜上一周期的跟踪残差，便于快反镜系统进行快速补偿。下一节将介绍整个复合轴系统的工作原理与跟踪残差补偿控制策略。

2.2 Risley双棱镜与FSM复合轴主轴偏差实时补偿

Risley双棱镜与FSM复合轴跟瞄系统利用RBF神经网络理论上可以无限逼近任意函数的优势，将Risley双棱镜跟踪残差预测值e(k)发送给FSM子轴实现主轴偏差实时补偿。本复合轴跟瞄系统工作分为五个阶段，其控制流程框图如图8所示，第一阶段为实验数据采集阶段，首先由探测器与Risley双棱镜粗跟踪系统闭环，让目标以不同的轨迹、不同的速度、加速度运动，采集对应的脱靶量，再提取百分之六十的数据作为神经网络训练集。第二阶段为网络训练阶段，以粗跟踪系统上一控制周期的偏差e(k)、目标此时的速度、加速度为网络输入层，该控制周期的偏差e(k+1)为输出值，不断调整权值w(k)，直到网络收敛，具有足够的精度。第三阶段为目标扫描捕获阶段，该阶段Risley双棱镜平台按照一定轨迹搜索目标并将其锁定在视场内。第四阶段为粗跟踪阶段，当目标出现在视场内，启动粗跟踪，探测器与Risley双棱镜粗跟踪平台形成闭环系统，控制器接收脱靶量并解算得到运动信号驱动Risley双棱镜快速旋转到目标位置，实现粗级跟踪；第五阶段为实时补偿精跟踪阶段，当目标稳定在FSM精跟踪视场内时，启动精跟踪，神经网络系统根据目标脱靶量及速度与加速度信息提前预测Risley双棱镜主轴的偏差，FSM精跟踪系统依据该偏差解算FSM旋转角度，并快速旋转到目标位置实时补偿主轴偏差。

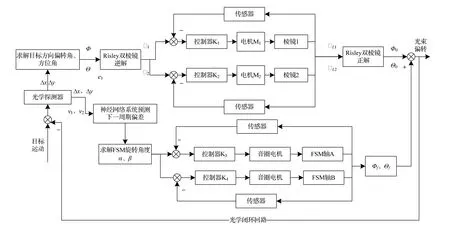
图8 Risley双棱镜与FSM复合轴主轴偏差实时补偿原理图

实时补偿精跟踪阶段，第k周期的脱靶量由Δx(k)、Δy(k)表示，粗跟踪系统跟踪残差为e1(k)。RBF神经网络预测值e1＇(k)，该值作为FSM精跟踪系统输入值，FSM输出值e2(k)即为实时补偿量。则Risley双棱镜与FSM复合轴跟瞄系统最终偏差为e(k)＝e1(k)－e2(k)，极大减小了跟瞄系统跟踪误差。

3 仿真实验

为了检验Risley双棱镜与FSM快反镜复合轴实时精密控制方法的可行性与跟踪精度，本文给出了该方法与传统控制方法的仿真实验比较分析。仿真实验在MATLAB环境中进行。假定目标在H＝2 km外，Risley双棱镜的扫描视场范围为±30°，FSM的视场调整范围为±1.5°，则在2 km外系统扫描范围为R＝1.2 km的圆区域。FSM的可调整视场范围为Rf＝52 m，镜头视场为r＝35 m的圆区域。前文已经阐明了由于双棱镜视轴偏转角大小只与两个棱镜旋转角只差Δθ有关，当目标直线运动时偏转角变化最快。为了便于分析双棱镜系统的跟踪性能，目标轨迹设定为一条直线：

Risley双棱镜粗跟踪平台X、Y方向上的跟踪效果如图9所示，蓝色曲线与绿色曲线分别代表目标X方向坐标与视轴中心X方向坐标，红色曲线与黑色曲线分别代表目标Y方向坐标与视轴中心Y方向坐标。两个棱镜旋转角度变化曲线如图10所示，蓝色曲线表示棱镜1的角度变化曲线，黑色曲线表示棱镜2的角度变化曲线。粗跟踪平台跟踪误差如图11所示，红色曲线表示X方向误差，蓝色曲线表示Y方向误差，由图可知当系统稳定后跟踪误差可以达到0.5 mrad。

图9 Risley双棱镜粗跟踪平台跟踪效果图

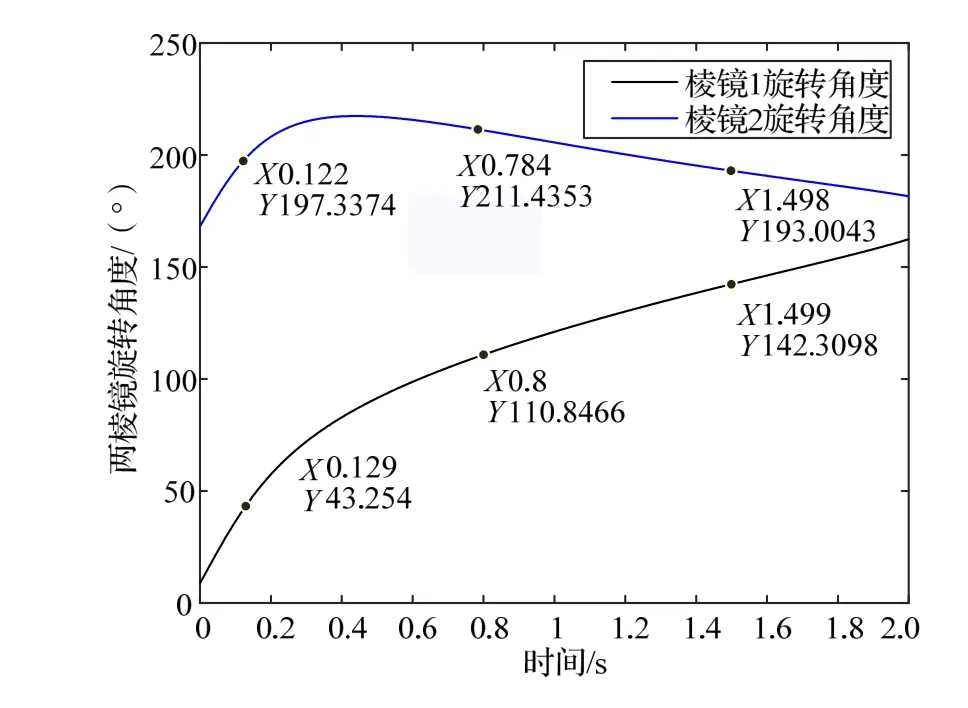
图10 Risley双棱镜粗跟踪系统两个棱镜旋转角度变化曲线

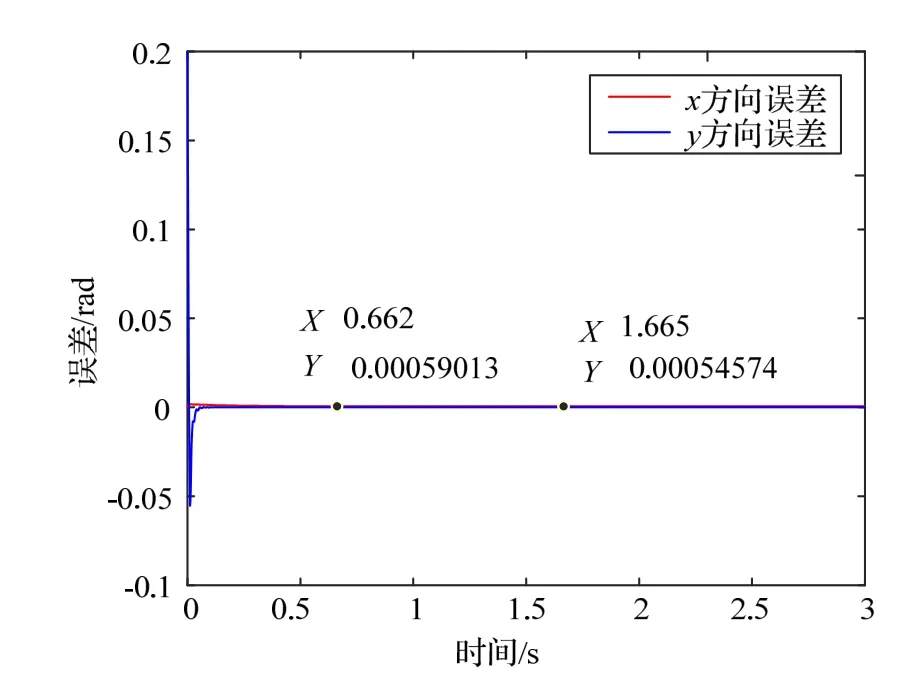
图11 Risley双棱镜粗跟踪系统x、y方向跟踪误差

传统方法与Risley双棱镜与FSM快反镜复合轴实时精密控制方法的仿真结果如图12所示，图13为局部放大图。图中方法一为传统控制方法仿真结果，方法二为本文提出的控制方法仿真结果。由图中可知本文所提出的控制方法有效提升了系统的响应速度与跟踪精度。传统方法跟踪波动较大，响应速度非常慢，波动范围在4～500 µrad，稳定后误差为4.88 µrad。而Risley双棱镜与FSM快反镜复合轴实时精密控制方法的跟踪误差波动非常小，基本在0.8～10 µrad，稳定误差可以达到0.89 µrad。

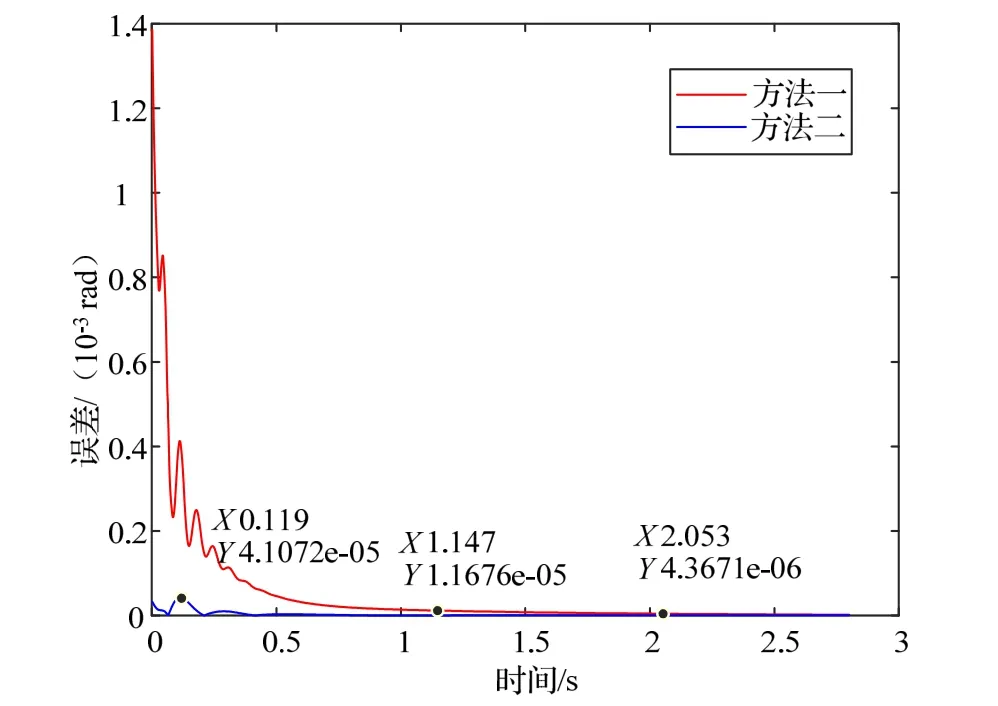
图12 传统方法与Risley双棱镜与FSM快反镜复合轴实时精密控制方法误差对比图

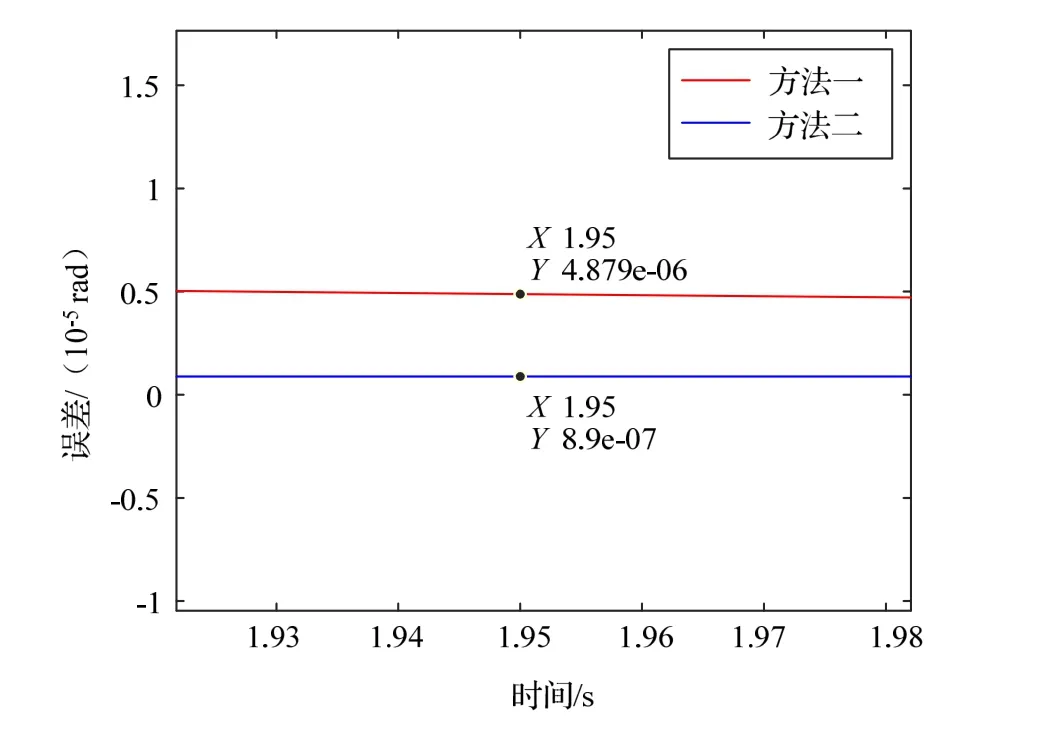
图13 图12局部放大图

4 总结

针对传统的单探测器复合轴跟踪控制方法粗精平台交接换班工作控制复杂，粗精对准矩阵难以精确定参，同时响应速度慢、控制精度低等问题，本文提出了一种Risley双棱镜与FSM快反镜复合轴实时精密控制方法。该控制方法利用RBF神经网络模型根据目标运动信息提前预测Risley双棱镜粗跟踪平台下一控制周期的跟踪误差err，并将该偏差信号提前发送给FSM精跟踪平台进行实时补偿。该过程不存在传统方法粗精平台交接换班工作的过程，也不需要对解耦之路精确定参，通过提前预测与实时补偿有效提高了复合轴跟瞄系统的响应速度与跟踪精度。本文在MATLAB环境下建立了传统复合轴控制方法与Risley双棱镜与FSM复合轴精密控制的实时预测与补偿方法仿真实验模型，并进行了控制效果对比仿真试验。实验结果表明本控制方法能够将复合轴跟踪误差从4.88 µrad降低到0.89 µrad，并且极大地提高了系统的响应速度与稳定性，验证了该控制方法的可行性。