机床线性轴多自由度运动误差在线测量方法*

蔡引娣，高英豪，王路辉，范光照

（大连理工大学，大连 116024）

多轴数控机床常被用于加工航空结构件复杂曲面，复杂曲面的面型精度取决于数控机床的加工精度。线性轴是数控机床的重要运动部件，其不可避免的制造误差和装配误差将影响数控机床的加工精度。误差补偿法可以在满足精度的情况下降低仪器和设备的制造成本，因此成为提高数控机床加工精度的主要手段[1]。

误差测量是误差补偿的基础，商用激光干涉仪可以通过搭配不同的镜组实现多自由度运动误差的测量。但是，每次只可测量单一误差，长时间的测量将增加环境的不确定度。随后，出现了多自由度运动误差同时测量的仪器，如API公司的激光6D测量系统[2]和Renishaw公司的XM–60多光束激光干涉仪。但这些系统体积大，无法集成在机床上进行在线误差测量，成本也较高。

为了满足小型化、易集成的要求，近年来出现了一些高精度的多自由度运动误差测量系统。Jin等[3]提出了基于外差干涉原理的直线度误差与滚转角误差同时测量方法。房丰洲[4]和Lee[5]等基于全息原理提出了一种六自由度误差同时测量方法。Feng等[6]基于激光干涉原理和激光自准直原理设计了用于测量线性轴六自由度运动误差的激光测量系统。Yu等[7]提出了基于声光调制和光纤耦合的运动误差测量方法。翟玉生等[8]基于激光准直技术提出了五自由度运动误差测量系统。Fan等[9]利用4套多普勒测量仪和两个光电探测器测量了线性轴的六自由度运动误差。上述测量系统具有较高的分辨率和测量精度，但是其测量范围较小，且光路复杂，很难用于机床误差在线测量。

Huang[10]和Cai[11–12]等提出了基于激光准直原理和激光自准直原理的多自由运动误差激光测量方法，并采用小型化半导体激光器作为测量系统的光源。测量系统体积小，可以集成在机床上进行误差测量。测量系统中考虑了由半导体激光器自身发热、机械振动和电噪声干扰等引起的激光发射端的光束漂移对测量精度的影响。但未考虑在测量过程中大气扰动对测量系统稳定性和测量精度的影响。同时，未考虑半导体激光器的椭圆光斑对测量系统测量精度的影响。

因此，本研究基于半导体激光器设计了一种光路简单、低成本、易集成的四自由度运动误差测量系统。提出了基于双反射镜的光束漂移主动抑制方法，采用BPNN–PID控制双反射镜的角度，使其旋转方向始终与光束漂移方向相反。研究了椭圆光斑对测量精度的影响，提出了通过改变聚焦透镜和光电探测器的相对位置来修整光斑形貌的方法。该方法不用加入其他光学元件，提高了系统的稳定性。最后通过一系列试验验证了提出方法的有效性和设计的四自由度运动误差测量系统的测量精度。

1 四自由度误差测量系统

1.1 测量原理及光路设计

四自由度运动误差测量系统光学结构简图，如图1所示。系统由固定端、测量端、比对端和反馈单元4部分组成。固定端用于发射激光，由半导体激光器 （LD）、直角反射镜（M1、M2）、分光棱镜 （BS1、BS2、BS3）组成。测量端用于四自由度运动误差测量，由BS4、M3、聚焦透镜（FL1）和四象限光电探测器 （QPD1、QPD2）组成。比对端光路与测量端光路结构一致，用于光束漂移抑制效果的对比测试，由BS5、M4、M5、FL2和QPD3、QPD4组成。反馈单元1和反馈单元2用于实时测量激光光束平行漂移和角度漂移，由QPD5、QPD6和FL3组成。

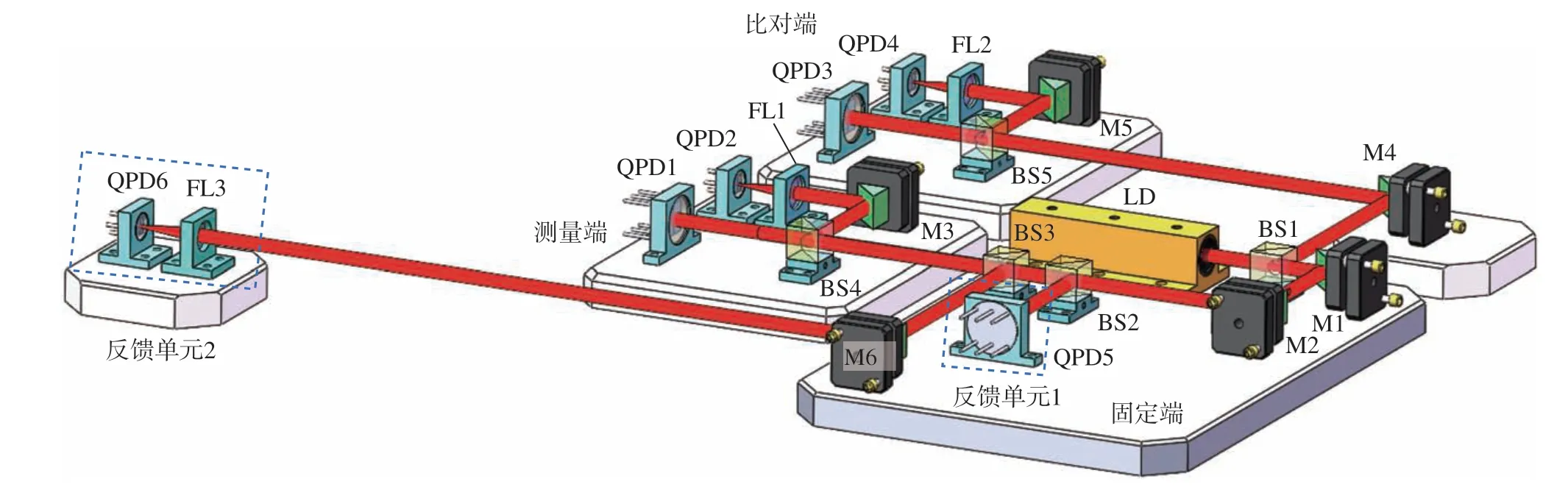
图1 四自由度运动误差测量系统Fig.1 4–DOF motion errors measurement system

激光光束由LD出射后，经过M1、M2反射并透过BS2、BS3射入测量端的直线度误差测量单元 （QPD1）和角度误差测量单元 （FL1和QPD2）。QPD由4个完全相同的光电二极管组成，当激光光束射至QPD的光敏面时，各象限将会输出响应电流，其电流值i与光敏面上接收光强度呈正比例关系。

直线度误差的测量基于激光准直原理。当线性轴在运动过程中不存在直线度误差时，光束将打在QPD1的中心位置处。此时，各象限的响应电流相等。当线性轴存在直线度误差（δx、δy）时，光束将在QPD1上产生沿X方向和Y方向的偏移量Δx1和Δy1。线性轴的直线度误差可由式（1）得到

式中，kδx、kδy为QPD1在X和Y方向上的灵敏度；im（m=A1，B1，C1，D1）为各象限的响应电流。

角度误差的测量基于激光自准直原理。当线性轴在运动过程中不存在角度误差时，光束将打在QPD2的中心位置处。当线性轴存在偏摆角误差和俯仰角误差（εx、εy）时，光束将在QPD2上产生沿X方向和Y方向的偏移量Δx2和Δy2。线性轴的偏摆角误差和俯仰角误差可由式（2）得到

式中，f为聚焦透镜的焦距；kεx、kεy为QPD2在X和Y方向上的灵敏度；in（n=A2，B2，C2，D2）为QPD2各象限的响应电流。

1.2 光束漂移抑制原理

为了提高测量过程中半导体激光器光束稳定性，提出了基于双反射镜的光束平行漂移 （平漂）和角度漂移 （角漂）主动抑制方法。光束漂移抑制原理如图2所示。激光光束由LD射出，被M1、M2反射后，经BS2分为两束光。其中，反射光射入QPD5用于平漂测量；透射光经过BS3后再次分为两束光，其透射光进入测量端用于运动误差测量，反射光经M6反射后被FL3聚焦至QPD6用于角漂测量。其中，M1和M2安装在内嵌有压电陶瓷驱动器 （PZT）的高精度二维角度调整架上。

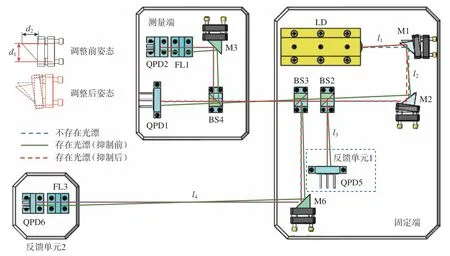
图2 激光光束漂移抑制原理Fig.2 Principle of compensating laser beam drift

当激光器存在平漂σx、σy和角漂τx、τy时，激光光斑在QPD5和QPD6上会产生沿X和Y方向发生偏移量。此时，根据偏移量和PZT驱动电压之间的关系改变PZT的长度，从而调整位于高精度二维角度调整架上M1和M2绕X轴和Y轴的转动角度αx、αy和βx、βy，使调整光线光轴与理想光束光轴重合。待重合后，QPD5和QPD6上的光斑位置会回到其中心位置，即实现了对激光平漂和角漂的实时抑制。

激光光束漂移主动抑制流程如图3所示。当QPD5、QPD6检测到光束的平漂和角漂信号后，信号经过I/V转换放大电路和A/D转换电路传至上位机作为BPNN和PID控制的输入信号。经训练后的BPNN实时调节PID控制器的参数 （kp、ki、kd），PID控制器对输入信号产生响应输出，其经D/A转换为PZT的驱动电压，改变高精度二维角度调整架中PZT的长度，从而改变M1和M2的角度，使光束始终位于QPD5和QPD6的中心。

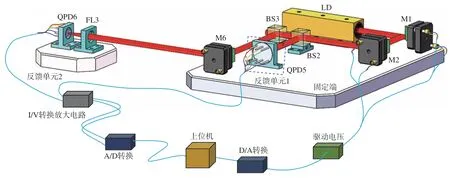
图3 激光光束漂移主动抑制流程Fig.3 Process of active compensating laser beam drifts

由上述分析和高精密二维角度调整架的结构可知，当射入M1和M2的光束没有经过高精度二维角度调整架的旋转中心时，M1和M2的旋转角将影响QPD5和QPD6的输出。因此，QPD5和QPD6的输出不仅受激光器平漂σx、σy、角漂τx、τy的影响，还受到M1旋转角度αx、αy和M2旋转角度βx、βy的影响。根据光束追迹法可得QPD5和QPD6的输出为

式中，δx5、δy5、εx6、εy6分别为QPD5、QPD6在X方向和Y方向的输出；d1为球铰与PZT间距；d2为反射镜直角边长；l1、l2、l3、l4为各元件之间光程，如图2所示。

由式（3）和（4）可解得直角反射镜M1和M2旋转角度与激光平漂和角漂的关系为

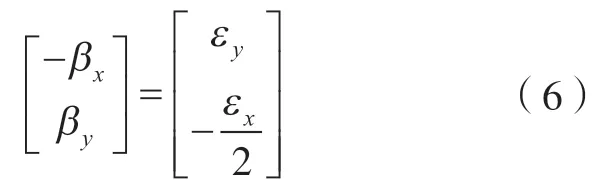
1.3 光斑畸变影响分析及解决

当采用传统的归一化差分算法计算光束位于四象限光电探测器的位置时，如式（7）所示，激光器光斑形状须为圆形。

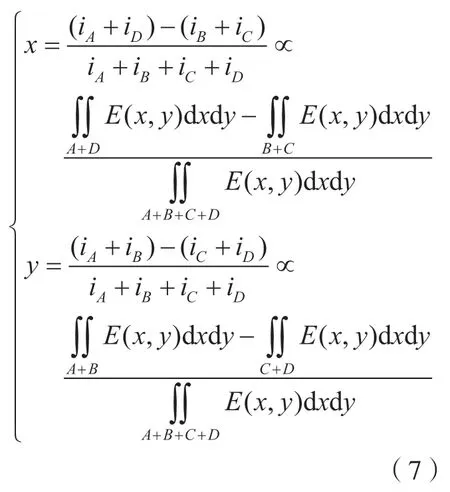
式中，E（x，y）为激光器光强。当激光器光斑为圆形时，激光器光强Ecir（x，y）可表示为

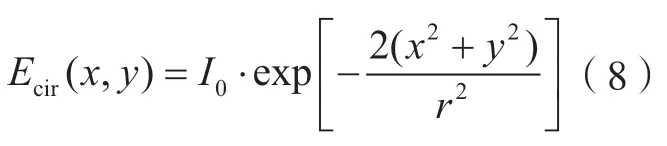
式中，I0为光斑质心光强度值；r为光斑半径。

而当激光器光斑为椭圆形时，其光强Eell（x，y）可表示为

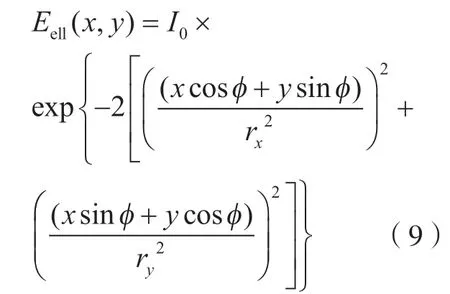
式中，rx、ry为椭圆光斑长半轴和短半轴长度；φ为椭圆光斑倾角。

对比圆光斑和椭圆光斑光强表达式可知，椭圆光斑的光斑大小和倾角将影响QPD的光束位移测量结果。本研究首先模拟分析了椭圆光斑的光斑形貌对直线度误差和角度误差测量精度的影响。由椭圆光斑造成的测量误差可由圆光斑的测量结果与椭圆光斑的测量结果之差得到。图4为模拟结果，椭圆光斑形貌对直线度误差测量精度影响较小，可以忽略 （图4（a））。而椭圆光斑形貌对角度误差测量精度影响较大，且随着椭圆光斑的减小，椭圆光斑造成的测量误差逐渐增大 （图4（b））。同时，由椭圆光斑造成的测量误差随倾角和椭率e（rx、ry之比）的增加而增加 （图4（c）和 （d））。

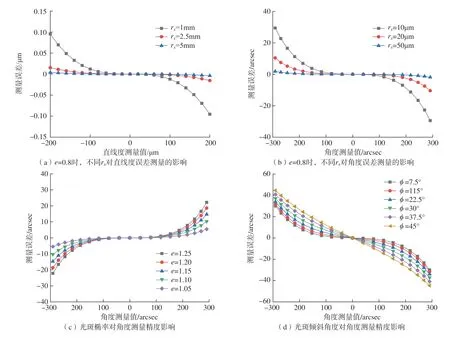
图4 光斑形貌对测量精度影响Fig.4 Influence of laser spot shape on measurement accuracy

为了消除椭圆光斑对测量结果的影响，本研究提出了通过改变聚焦透镜和四象限光电探测器的相对位置来消除椭圆光斑造成的测量误差的方法，其原理如图5所示。当四象限光电探测器位于聚焦透镜的焦平面时，聚焦后打在四象限光电探测器上光斑的长轴和短轴 （xf和yf）可由式（10）计算得到

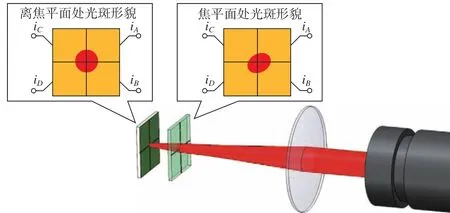
图5 激光光斑整形原理Fig.5 Principle of laser beam shaping

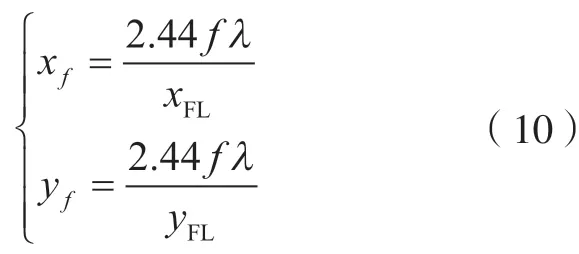
式中，xFL、yFL分别为聚焦前光斑长轴和短轴；λ为激光波长。

当四象限光电探测器到聚焦透镜的焦平面的距离为d时，聚焦后打在四象限光电探测器上光斑的长轴和短轴 （xd和yd）变为

由式（11）可知，当四象限光电探测器到聚焦透镜的焦平面的距离为d，如式（12），聚焦后打在四象限光电探测器上光斑的长轴等于短轴，即椭圆形光斑被整形为圆形光斑。

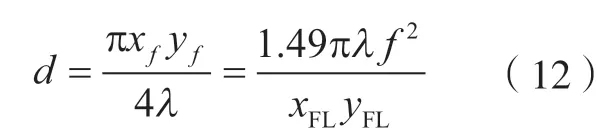
由图6可知，将光斑整形为圆形的同时，四象限光电探测器安装位置偏离理想焦平面将引入测量误差Δεx和Δεy

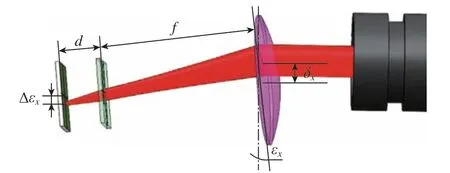
图6 离焦对测量精度的影响Fig.6 Effect of defocused on measurement accuracy

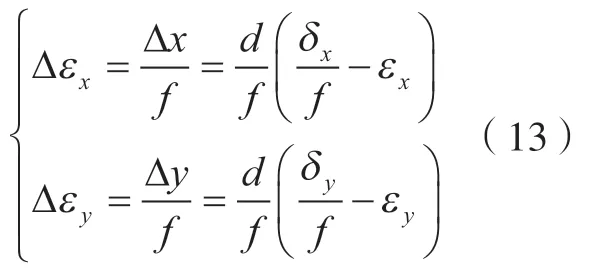
Δεx和Δεy为系统误差，其对运动误差测量系统测量精度的影响可以通过式（13）来消除。

2 试验与分析

根据上述测量和补偿原理，搭建四自由度运动误差测量系统，如图7所示。半导体激光器选用西安华科光电有限公司的DA635型激光器。四象限光电探测器选用First Sensor公司的QP5.8–6–TO5和QP50–6–T08型四象限光电探测器。PZT采用TOKIN公司的AL1.65×1.65×5D–4F型压电陶瓷致动器。

图7 试验装置Fig.7 Experimental setup

首先，通过标定试验计算各四象限光电探测器的灵敏度，以席尔瓦克 （SYLVAC）公司的805.8601型电子数显千分表和奥特梅尔公司的AUTOMAT 5000UH–3050型光电自准直仪作为标定测量直线度误差和角度误差的QPD1和QPD2的标准仪器。千分表和光电自准直仪的测量精度分别为±0.8μm和±0.1arcsec。用于测量直线度误差的QPD1的灵敏度标定结果如图8（a）所示，在±300μm标定范围内，X方向灵敏度为1860.9 μm/V，Y方向灵敏度为1652.4μm/V。根据提出的光斑整形的方法，不断地调整QPD2与FL1之间的距离，直到标定范围在±300acrsec内时QPD2在X方向和Y方向的灵敏度近似相等。X方向灵敏度为1346.9arcesec/V，Y方向灵敏度为1337.0arcesec/V，如图8（b）所示。由于，灵敏度和光斑直径呈线性关系，所以此时椭圆光斑已经被整形为圆光斑。

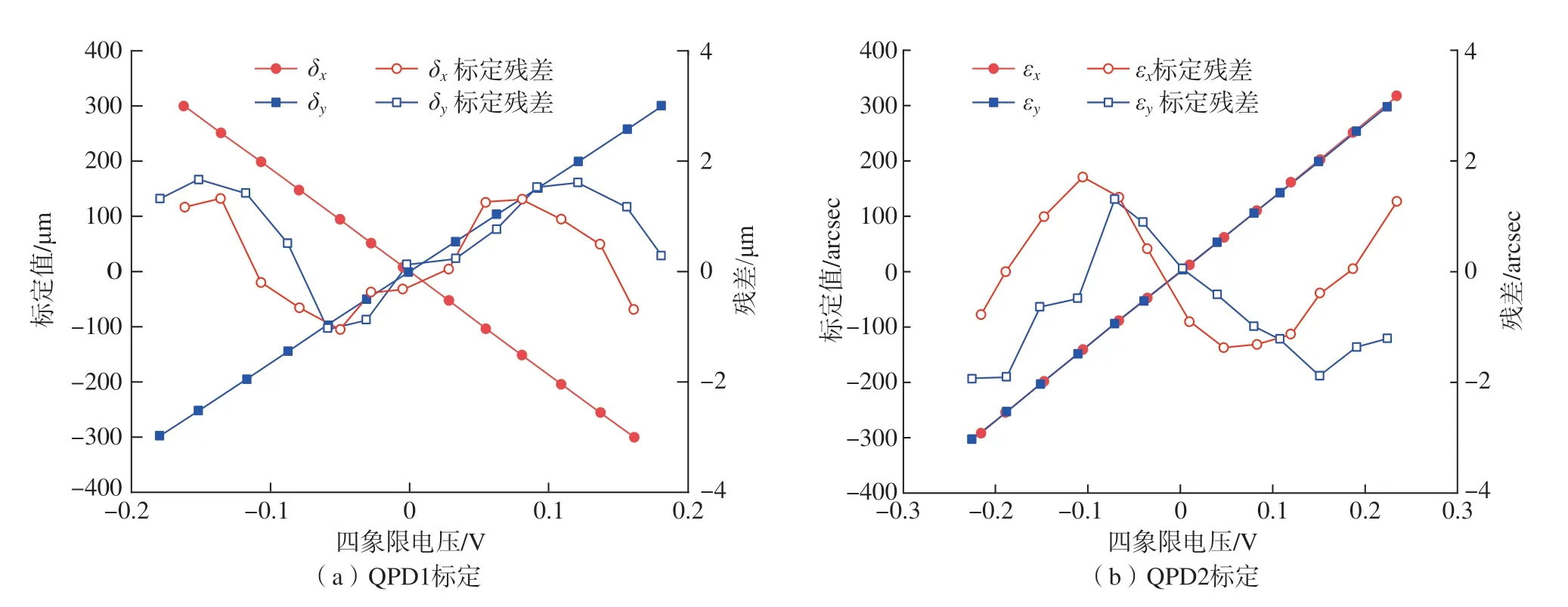
图8 QPD1和QPD2标定Fig.8 Calibration of QPD1 and QPD2

其次，对测量系统的稳定性进行测试。为了验证提出的光束漂移抑制方法的有效性，设计并搭建了和测量端具有同样光学结构的比对端。在测试中，测量端采集的数据为光束漂移抑制系统开启状态下的数据，而对比端为光束漂移抑制系统不开启状态下的数据。将测量端与比对端装置同时安装于距离固定端1400mm处。采用小波滤波串联中值滤波的组合滤波方式，采样频率和采样时间设为20Hz和1800s。稳定性测试结果如图9所示。水平直线度误差信号δx、竖直直线度误差信号δy、偏摆角误差信号εx和俯仰角误差信号εy的稳定性由光束漂移抑制前的6.9μm、6.7μm、5.4arcsec和4.6arcsec提高到光束漂移抑制后的5.5μm、2.5μm、1.3arcsec和1.7arcsec。由此验证了本文提出的光束漂移抑制方法的有效性。

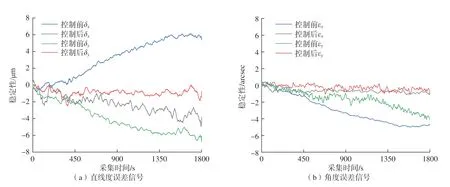
图9 光束漂移抑制前后系统稳定性Fig.9 Stability of measurement system before and after laser beam drifts compensation

最后，用设计的四自由度运动误差测量系统测量线性轴（瑞芯科技RXS60直线模组）的直线度误差δx、δy和角度误差εx、εy。被测线性模组运动行程为1200mm。为了验证设计的测量系统的测量精度，商用运动误差测量仪器也安装在线性轴上同时测量δx、δy、εx和εy。商用运动误差测量仪器的直线度误差测量精度为±1μm，角度误差测量精度为±0.5arcsec。进行3次测量，测量间距为100mm，测量结果如图10所示。残差表示商用运动误差测量仪器测量结果与设计的运动误差测量系统测量结果之差。其中，δxi、δyi、εyi、εyi（i=1，2，3）表示由本研究所设计的运动误差测量系统测量得到的运动误差；δxi′、δyi′、εyi′、εyi′（i=1，2，3）表示由商用运动误差测量仪器测量得到的运动误差。由图10可知，水平直线度误差δx和竖直直线度误差δy测量残差均小于±1.9μm，偏摆角度误差εx和俯仰角度误差εy测量残差均小于±1.6arcsec。

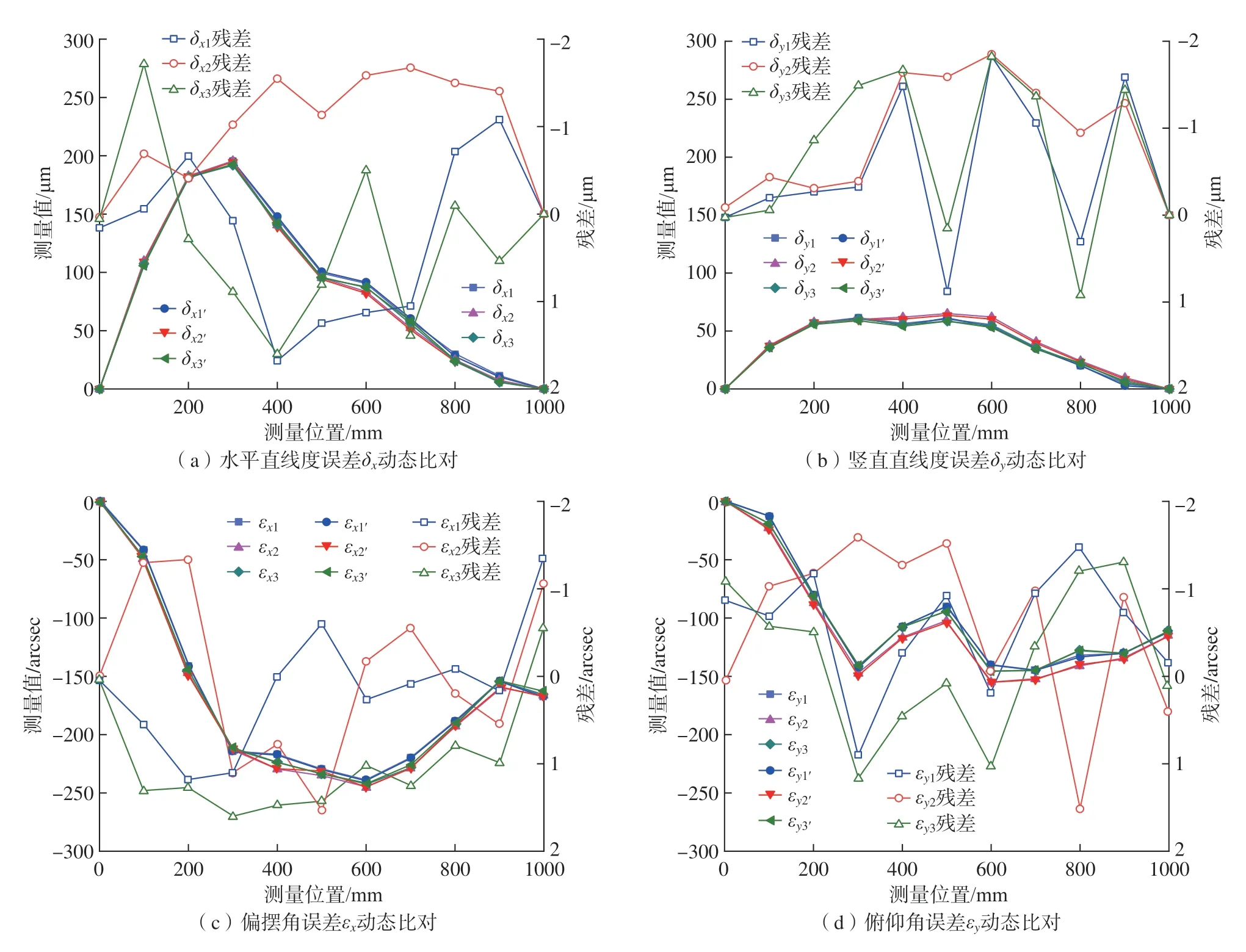
图10 线性轴四自由度运动误差测量结果Fig.10 Measurement results of 4-DOF motion errors of linear stage

3 结论

（1）设计了以半导体激光器为光源的低成本、易集成、高精度的四自由度运动误差测量系统。

（2）提出了基于双反射镜的激光光束平行漂移和角度漂移自动抑制方法；水平直线度误差信号、竖直直线度误差信号、偏摆角误差信号和俯仰角误差信号的稳定性由光束漂移抑制前的6.9μm、6.7μm、5.4arcsec和4.6arcsec提高到光束漂移抑制后的5.5μm、2.5μm、1.3arcsec和1.7arcsec。

（3）分析了椭圆光斑对运动误差测量精度的影响，并提出了通过改变聚焦透镜和四象限光电探测器相对位置来改变光斑形貌的方法。

（4）通过测量试验得到设计的四自由度运动误差测量系统直线度误差测量精度为±1.5μm，角度误差测量精度为±1.5arcsec。