工业机器人绝对定位误差补偿方法*

林嘉睿， 程东源， 刘思仁， 任永杰

（1.天津大学精密测试技术及仪器国家重点实验室，天津 300072；2.中国商飞上海飞机制造有限公司，上海 200436）

航空制造过程中需要对机身和机翼的主要构件完成加工、铆接、装配等工序，该类作业任务往往具有大空间及高精度的特点，对作为制造装备执行体的工业机器人绝对定位误差提出越来越高的要求[1–3]。在实际生产中，机器人长期处于连续高速运行状态，关节磨损、连杆变形等几何误差因素以及电机发热、自重、负载等非几何因素作用使得机器人末端位置发生漂移，实际运行轨迹偏离设定值，且定位误差是动态变化的，导致绝对定位精度显著下降。因此，需要研究一种工业机器人绝对定位误差的高效补偿方法，在不影响作业节拍的前提下在线提升机器人的绝对定位精度。

已有的补偿方法通常是在离线状态下对机器人的运动学参数进行标定[4–6]，然而机器人误差源繁多，这种方法只能一定程度上消除制造、装配等因素造成的几何参数误差，不能改善因电机发热，外界温度变化、末端负载作用等非几何参数因素造成的绝对定位误差。文献[7–11]提出在机器人末端增加视觉传感器，基于距离约束和球约束关系建立优化模型实现在线自标定，对测量工具要求简单，可用于补偿因非几何参数因素导致的绝对定位误差，但每次标定只在特定工作空间内采集少量的位姿信息，无法对全空间内的定位误差实现有效补偿。文献[12–13]通过外部高精度测量设备对工业机器人的位姿进行实时测量，辨识实际运动学参数并反馈给机器人，但测量设备效率低，容易发生遮挡，同时不支持无法在控制器中修改运动学参数的机器人。文献[14–17]通过事先设计好的固定空间网格结构，利用激光跟踪仪建立机器人位置和对应误差矢量值之间的映射变换，对几何及非几何因素导致的绝对定位误差均有一定补偿效果，但该方法仍存在以下不足： （1）定位误差在机器人作业过程中是动态变化的，且随着机器人作业空间的变换，精度的维护需要对空间误差库进行实时更新，跟踪仪无法短时间内完成，补偿实时性不强； （2）跟踪仪等单站式测量设备无法高效实现全空间和全位姿的测量； （3）空间网格边长即网格划分疏密程度影响插值结果准确性和误差库建立效率，现有方法无法根据空间绝对定位误差实际分布情况实时调整网格边长。

针对以上问题，本研究利用工作空间测量定位系统wMPS （Workspace measurement positioning system）高精度、动态测量特点实现了空间误差库的快速建立并可随着机器人工作空间及工作姿态的变化及时更新误差库，研究了基于反距离加权插值算法的工业机器人绝对定位误差补偿方法，提出了一种边长可调的空间网格精细划分方法，动态调整网络划分既保证了插值结果的精度也进一步提升了误差库建立效率。wMPS作为一种多基站多目标并行测量系统，单站测角精度可达2"，测量频率可达30Hz，可以实现空间三维坐标的高效自动测量[18]，且可以根据现场情况灵活布局提升对机器人工作空间和位姿的覆盖能力，克服一定的光路遮挡，具有较强的现场适应性，在不影响作业节拍情况下，可以满足机器人绝对定位误差在线补偿的测量需求。

1 工作空间测量定位系统

wMPS是一种典型的分布式测量系统[18]，在空间不同位置摆放多台激光发射站，每台发射站通过精密转台带动两扇形扫描光面进行高匀速旋转，结合同步光信号构建全周向光场，能够覆盖空间多个光电接收器，基于多站角度交会约束实时获取接收器空间三维坐标信息。

图1为wMPS坐标测量示意图，发射站向测量空间发射两束绕轴匀速旋转并带有一定倾角的扫描激光平面1和2，同时当平面转到预定位置处基站发射光脉冲作为同步标记，当接收器收到发射站的扫描光平面信号或同步标记信号时进行光电信号转换，通过同步光–扫描光的相位信息来计算基站所测量的角度值，如图2所示。

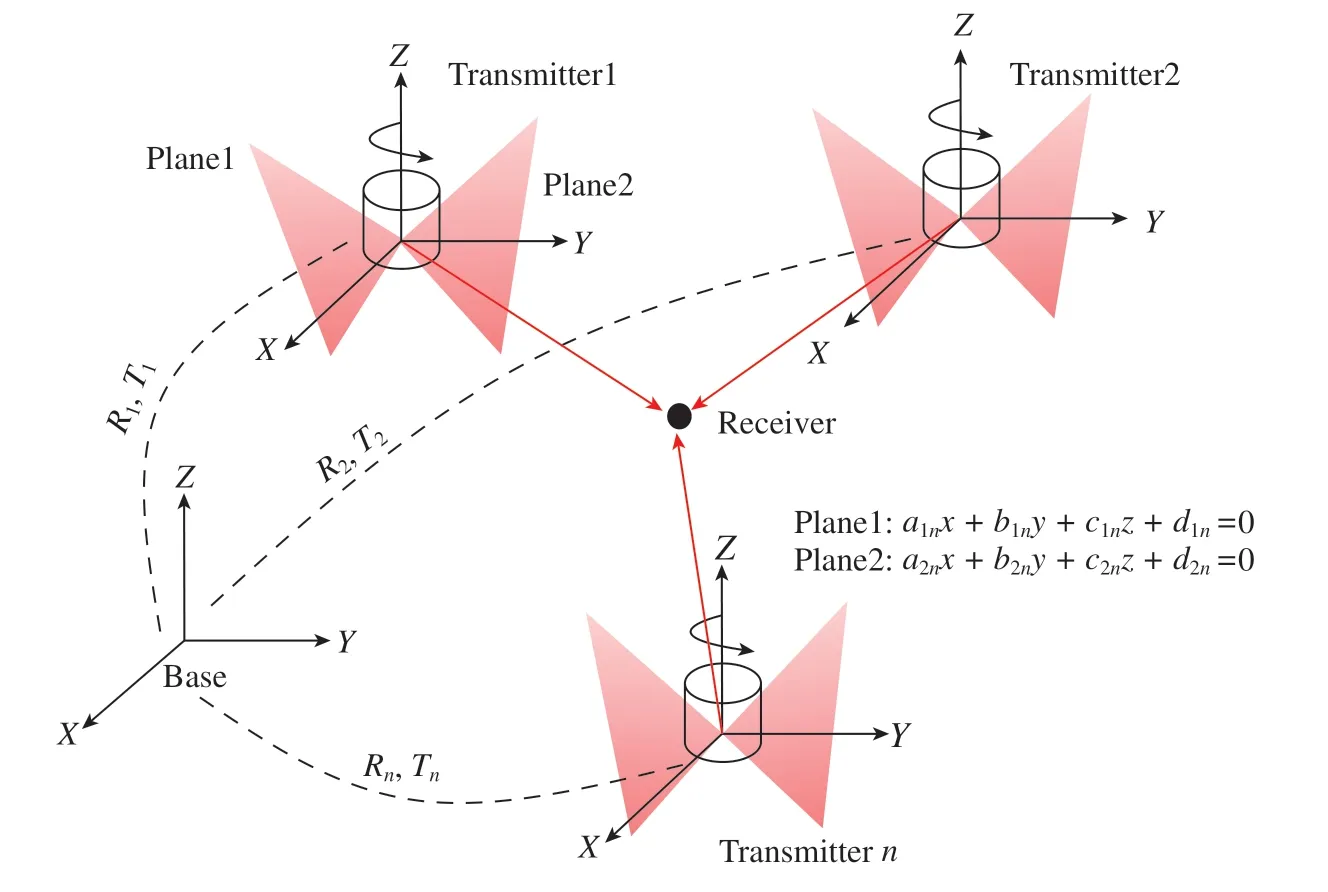
图1 wMPS测量示意图Fig.1 Schematic diagram of wMPS

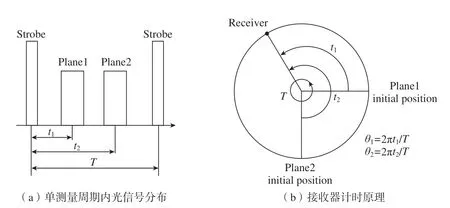
图2 单站测角原理Fig.2 Principle of single station angle measurement

此时，在发射站坐标系下的平面方程系数变为旋转角度θ1、θ2的函数为

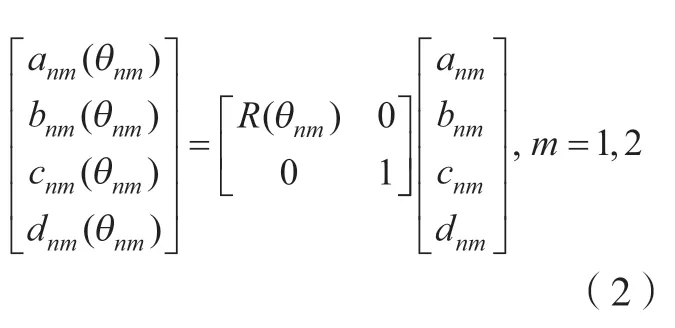
式中，a、b、c、d为发射站扫描光平面方程系数；m为发射站扫描光平面序号；n为发射站序号。

当系统基站完成姿态定向后，发射站坐标系到测量坐标系的旋转矩阵RTXG及平移向量PTXG已知，记发射站两扫描光平面到达待测接收器旋转角度为θn1和θn2。

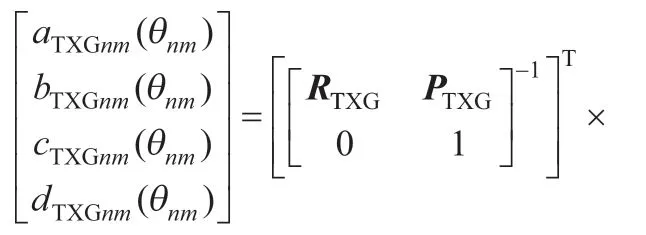
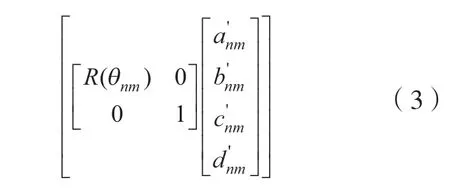
式中，n∈N；m=1，2；TXG为测量坐标系下的发射站结构参数。

此时在测量坐标系下坐标PRXG（xRXG，yEXG，zRXG）T

当测量空间内有n（n≥2）台发射站时，可以列出2n个方程，对这些方程组成的超定方程组进行最小二乘求解即可得到接收器的坐标PRXG。其中，发射站的转速和信号处理器的处理速度均会影响wMPS测量频率。不同发射站的识别基于不同的转速参数，接收器在一个测量周期内收到同一发射站的同步光信号和两个扫描光信号才能保证数据有效，目前发射站转速可稳定在1800～2500r/min区间，信号处理器处理光电信号频率稳定为30Hz，wMPS单点测量时间约为33ms，该动态性能为后续空间误差库的快速建立及更新打下了基础。

2 机器人位置误差插值补偿

以六自由度工业机器人为例，其运动过程中的变量仅为各关节轴的转角，随着各轴旋转角度的变化，其相应位置的绝对定位误差值也会随之变化，且该变化趋势在工作空间内是连续的，并在一定范围内可视为线性变化[19]。通过确定绝对定位误差显著线性相关的空间距离，合理划分空间网格并采集网格节点处绝对定位误差值，则空间内任意位置处的绝对定位误差值便可通过线性插值得到。为进一步提升网格划分效率和插值计算的准确性，在整个工作空间内均匀随机选取若干点，并计算空间内任意两点绝对定位误差矢量值之间的相关性关系，依据满足显著线性相关的最大距离将空间粗划分为若干区域，之后根据绝对定位误差的变化趋势，调整网格边长进行各区域细划分，完成空间误差库的建立。

2.1 空间绝对定位误差相似度分析

在机器人工作空间内进行随机采样，获取采样点绝对定位误差信息，分析空间内两点距离值与对应定位误差差值之间的相关性关系，以ABB IRB6700–200/2.60型机器人为例，以机器人基坐标系作为参考坐标系，选取工作空间为1000mm×1000mm× 500mm，在机器人末端法兰盘上放置wMPS光电接收靶球。首先采用文献[20]的方法标定出机器人基坐标系与wMPS坐标系的转换关系，并标定出光电接收靶球球心相对于末端法兰中心的位置偏移量。如图3所示，在空间内随机选取243个姿态一定的采样点，测量各采样点处靶球中心坐标值，计算各点处的绝对定位误差值。

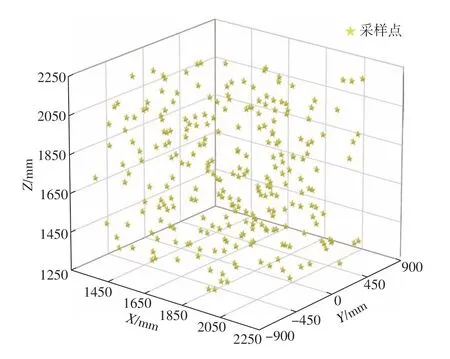
图3 工作空间采样点示意图Fig.3 Schematic diagram of sample points in workspace

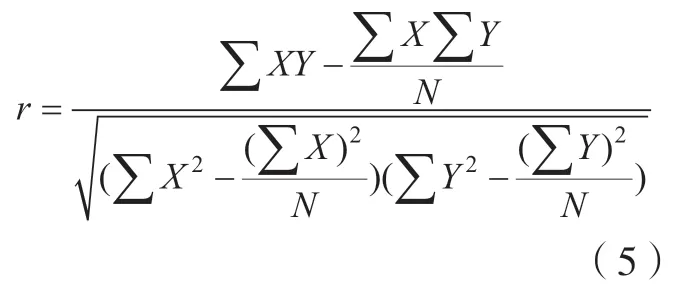
计算两采样点间空间距离与对应绝对定位误差差值间的相关程度，并采用Pearson系数评价，其计算公式为式中，X为两采样点间的空间距离；Y为两采样点对应绝对定位误差差值；r为相关系数，r>0时，表示两变量正相关，r<0时，表示两变量负相关，|r|的大小反映了两变量的线性相关高低，且已知当r≥0.70时，便可认为两变量间为显著线性正相关关系[18]。

图4拟合结果计算得到采样点间空间距离和对应绝对定位误差差值的Pearson相关系数值约为0.80，说明二者存在显著线性正相关关系，在合理完成空间误差库建立后可以通过线性插值的方式利用误差库中信息预测空间内任意目标点的绝对定位误差矢量值。

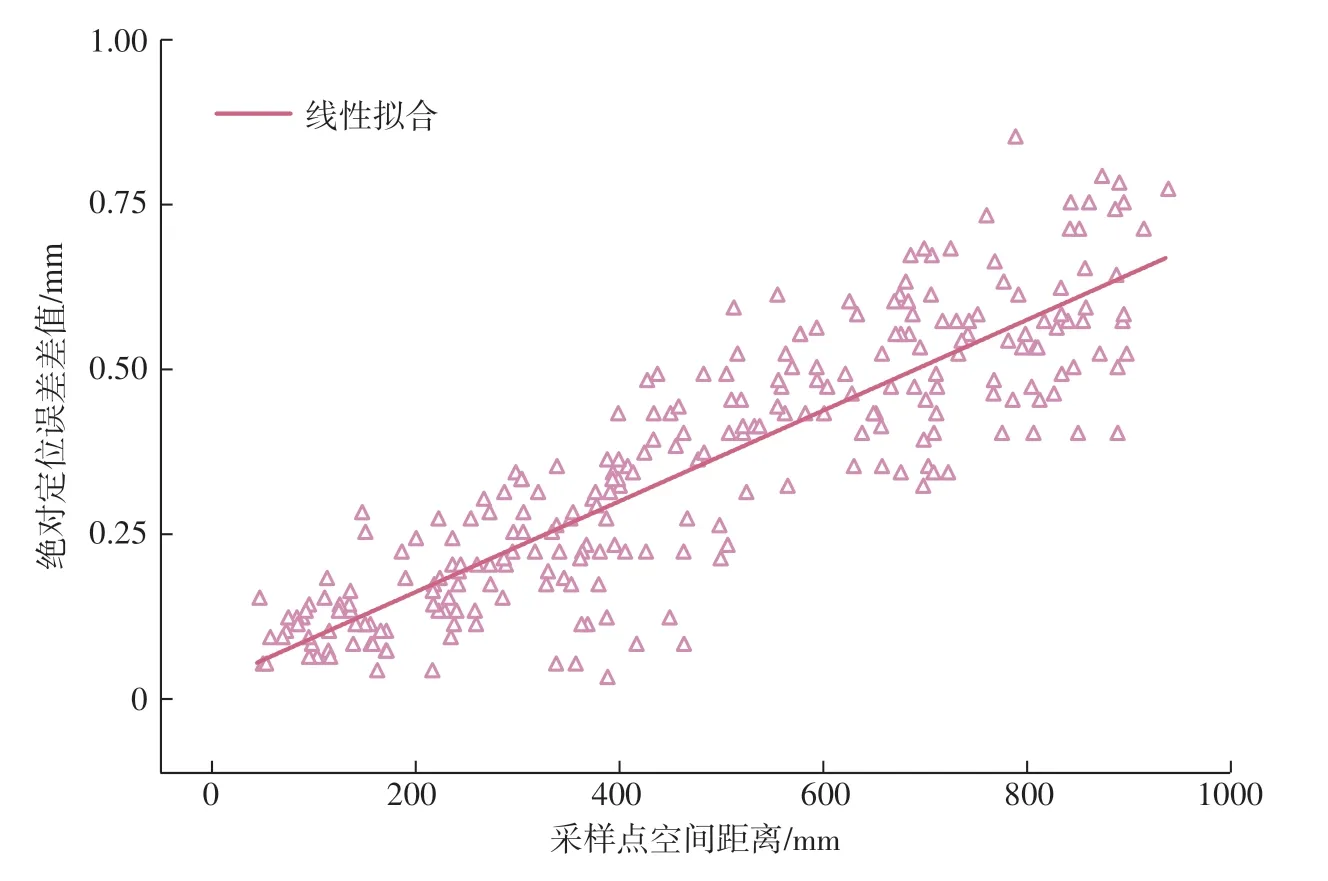
图4 采样点间空间距离与对应绝对定位误差差值的相似度关系Fig.4 Similarity relationship between spatial distance between sampling points and difference of absolute positioning errors

为研究随采样空间范围变化，采样点间空间距离和对应绝对定位误差差值的Pearson系数变化趋势，在原长方体空间的基础上逐渐减小空间范围，并选择各空间范围内的采样点依次按照式（5）的方式计算对应Pearson系数值，结果如图5所示。

由图5可知两点X、Y、Z方向绝对定位误差的差值与两点空间距离值之间的Pearson系数值随采样空间的减小而增大，以试验选取的采样空间为例，当空间两点距离≤400mm时，X、Y、Z3个方向对应的定位误差值均具有显著线性正相关性，即可得出类比结论：在一定的空间距离内，机器人X、Y、Z方向的绝对定位误差具有显著线性正相关性，在空间内设计合理的采样策略后，建立空间误差库，通过线性插值计算的方式可以实现定位误差值的提前预测。

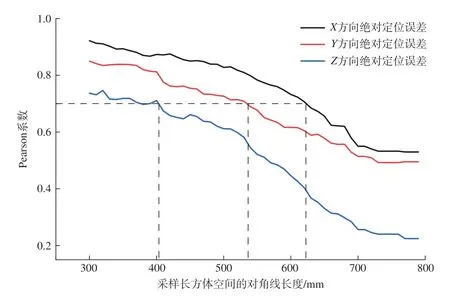
图5 采样空间对Pearson系数的影响趋势图Fig.5 Influence trend chart of sampling space on Pearson coefficient

2.2 空间插值法原理

已知机器人末端绝对定位误差矢量间的相似关系在笛卡尔空间的小范围内为显著线性正相关，不存在突变，因此在局部选取均匀分布的空间点进行线性插值计算，其逼近程度较好且计算简单、运算速度快。本研究采用的插值方法为反距离加权法。反距离加权法将两点间距离的倒数作为权重，即距离相近的点影响的权值因子更大，距离越远影响的权值因子越小，该方法对于连续缓慢变化数据插值效果好[21]。

根据机器人的运动轨迹选定待标定的工作空间，将该工作空间划分为一系列连续的空间网格，将网格顶点作为采样点，待标定空间内任意目标点的绝对定位误差矢量可以由包含其网格的8个节点处的绝对定位误差矢量插值得到。

如图6所示，完成空间网格划分后，首先测量出包含待测点的网格顶点（P1，P2，P3，…，P8）处的绝对定位误差值 ，以各顶点到待测点距离的倒数作为衡量各点权重的标准，将权值和绝对定位误差值相乘后求和即可预测网格中任意待测点P的绝对定位误差值。

图6 反距离加权法示意图Fig.6 Schematic diagram of inverse distance weighting method

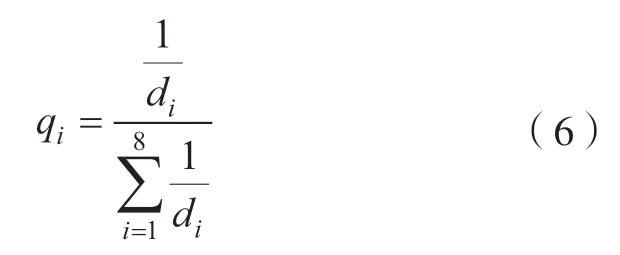
式中，qi为网格顶点Pi对P的影响权值；di为网格顶点Pi与P之间的距离。

式中，E为P的绝对定位误差矢量预测值；Ei为Pi的绝对定位误差矢量测量值。

2.3 网格边长设计

在进行空间网格插补时网格边长对插值结果的准确性有明显影响，边长太大采样点与预测点绝对定位误差矢量相似度太小，会导致插值结果不准确，减小边长可以提升插值结果的准确性，但会增加工作量，因此在实际补偿前需要选取合理的网格步长和划分策略。

在空间误差库建立过程中机器人需要多次重复启动–停止过程以完成采样，为尽可能缩短采样时间，需要确定机器人每次停留的最短时间t以区分采样点与路径上一般点，即

式中，t为采样时长，ms；T为wMPS单次测量耗时，ms；c为比例系数， 根据试验实际结果选取，为正整数。

2.3.1 网格粗划分

首先根据机器人运动轨迹确定工作空间范围为Lx×Ly×Lz，在空间内随机均匀选取足够多的采样点测得其绝对定位误差矢量以研究空间距离与绝对定位误差差值之间的相似度关系，参照2.1节内容，以Pearson系数等于0.70的空间距离值L作为粗划分立方体网格对角线长度值从而计算网格边长粗值a，见式（9），通过除以a向上取整的方式进一步得到工作空间X、Y、Z各方向的均分份数nx、ny和nz，见式（10），完成网格粗划分，划分后结果如图7所示。

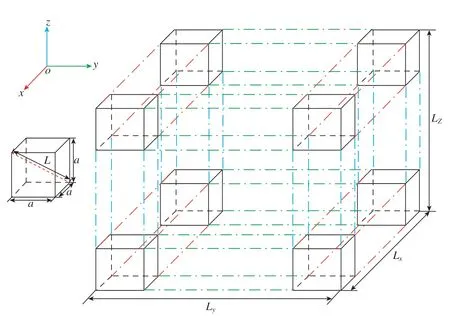
图7 空间网格粗划分示意图Fig.7 Schematic diagram of spatial grid roughly divided

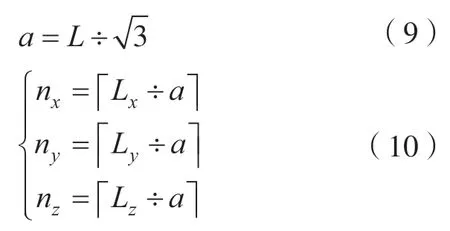
2.3.2 网格细划分

将工作空间粗划分为nx×ny×nz个网格区域后，选取各网格的中点位置作为起始点，利用wMPS系统测量效率高的优势，控制机器人在基坐标系下从起始点分别沿X、Y、Z方向做直线运动至且每间隔h做短暂停留t，各方向的最后一个采样点为当前网格区域边界，测量直线运动轨迹上各停留点的坐标值，进而得到各点对应的绝对定位误差矢量值，即

式中，k根据机器人实际运行节拍取值范围为[5%，10%]。

以图8所示方式完成测量后，按照到中心点距离由大到小的顺序，将距离相同的采样点分组进行反距离加权插值计算，得到中心点绝对定位误差矢量预测值Ein，计算与wMPS直接测量获取的中心点绝对定位误差矢量真实值Emn的偏差en，若en满足式（12）则继续计算en+1并判断两偏差值是否满足式（13），若满足则选取第n次距离值l作为细划分网格的对角线长度值，如图9所示。

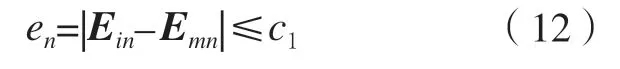
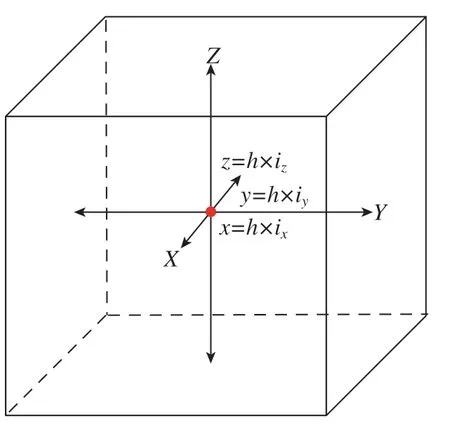
图8 细划分网格边长确定方法示意图Fig.8 Schematic diagram of method for determining side length of mesh subdivision

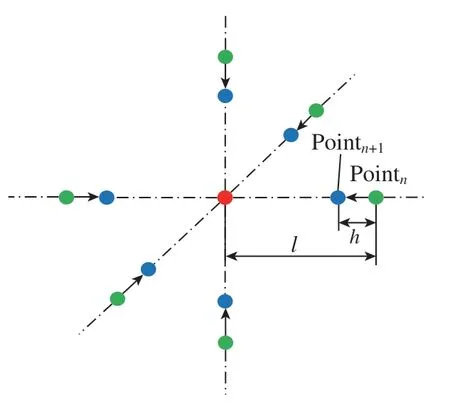
图9 细划分网格对角线长度l确认示意图Fig.9 Schematic diagram of confirming diagonal length l of mesh subdivision

式中，n为第n组采样点数据（按到中心点距离从大到小顺序分组排列）；c1为定位误差插值预测值与真实值偏差的阈值；c2为en和en+1差值的阈值。

以在该网格区域内满足式（12）和（13）的最大距离值l作为细划分网格的对角线长度值，区域大小为Lix×Liy×Liz，内部进行细划分时X、Y、Z方向均分份数nix、niy、niz的计算同式（9）和（10）。同理在其余粗划分区域完成网格细划分，建立空间误差库，最终的空间网格划分示意图如图10所示。

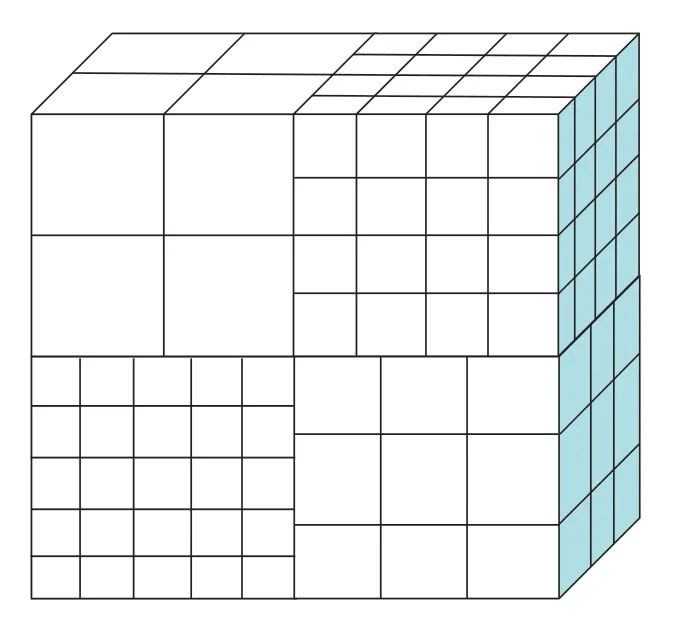
图10 空间网格划分示意图Fig.10 Schematic diagram of spatial grid division

3 试验验证与分析

为验证面向航空制造所研究方法的可行性及补偿后工业机器人的绝对定位精度，以ABB公司生产的IRB6700–200/2.60型机器人为研究对象，其重复定位精度Er= 0.10mm，网格节点绝对定位误差值测量采用wMPS，误差补偿效果验证采用Leica AT403型激光跟踪仪，测量精度为15μm+6μm/m。

以基坐标系作为参考坐标系，空间范围为：X方向1200～2200mm，Y方向– 500 ～500mm，Z方向1700 ～ 2200 mm，补偿过程中wMPS测量频率为30Hz。为在所采集坐标信息中挑选出采样点坐标值，机器人需频繁启停以标记采样点，为尽可能缩短采样时间，需要确定机器人在采样点处停留的最短时间，具体操作步骤如图11所示。

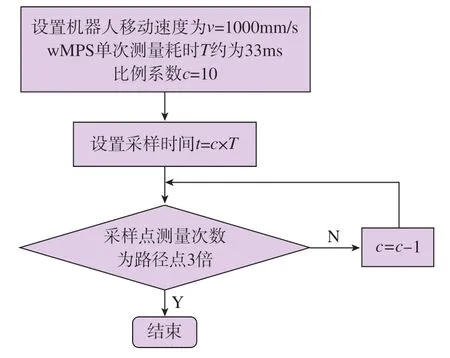
图11 节点最优停留时间选取流程图Fig.11 Flowchart for selecting the best pause time at nodes

试验结果显示，当前参数设置下当机器人在采样点处的停留时间约为100ms时可以将采样点坐标值与路径点坐标值进行明显区分。

为验证所提出误差补偿方法在实际生产中的补偿效果，特设置对比试验，比较机器人末端法兰在空载和安装约20kg蓝光形貌测量传感器后绝对定位误差的补偿效果，试验流程如图12所示。

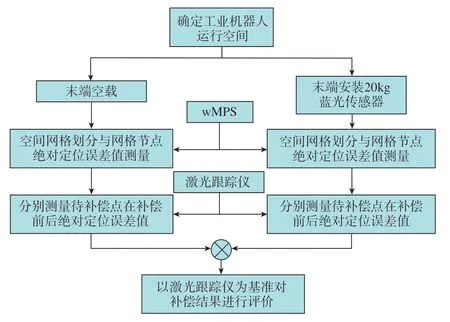
图12 机器人空载与20kg负载下绝对定位误差补偿对比试验流程图Fig.12 Experimental flowchart of comparison of absolute positioning error compensation by no–load and 20kg load

所搭建的试验验证平台如图13所示。

图13 试验验证平台Fig.13 Experimental setup

按照2.3节所介绍方法，参数设置为k=10%，c1=0.15mm，c2= 0.02mm，完成空间网格划分，得到的网格划分结果如表1所示。

表1 空载和增加20kg负载后空间网格划分结果统计表Table 1 Statistical table of meshing results of no–load and 20kg load

在空载和20kg负载两种情况下通过网格划分后分别建立wMPS空间误差库，在工作空间内均匀随机选取150个补偿点完成绝对定位误差补偿，以激光跟踪仪为测量基准，补偿前后的绝对定位误差值如图14所示。

由图14数据分析可知，空载情况下补偿点处绝对定位误差的平均值和最大值由补偿前的0.79mm和1.09mm减少至补偿后的0.16mm和0.25mm，分别减少了80%和77%，当在末端法兰增加20kg负载后，平均值和最大值由补偿前的1.36mm和2.09mm减少至补偿后的0.19mm和0.27mm，分别减少了86%和87%，增加负载后的误差补偿效果与空载时相当，证明了所提出方法的实际可行性。

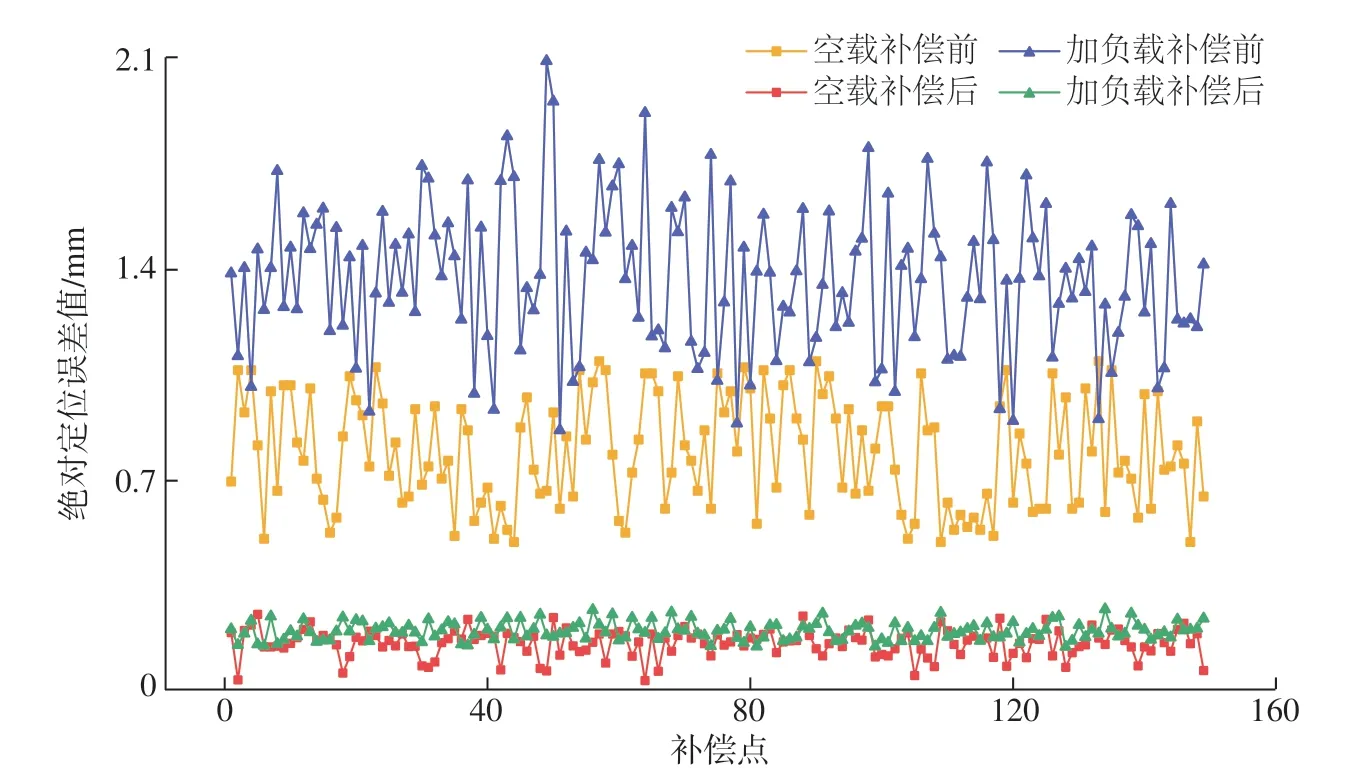
图14 不同负载下绝对定位误差补偿结果比较Fig.14 Comparison of absolute positioning error compensation by different load

为进一步说明采用wMPS建立空间误差库进行机器人绝对定位误差补偿耗时短的优势，基于图12的流程，比较了采用wMPS和激光跟踪仪完成空间网格化的效率和对应误差库补偿的效果。以激光跟踪仪为测量基准，两种方法耗时对比如表2所示，补偿前后的绝对定位误差如图15所示。

由图15的数据计算可知，使用wMPS和激光跟踪仪建立空间误差库完成误差补偿后，对应绝对定位误差的平均值分别为0.16mm和0.14mm，二者补偿效果相当。表2数据显示使用wMPS补偿流程总耗时3.6min，仅为使用跟踪仪自动测量耗时的28%，体现出wMPS测量高效性。且粗划分网格过程在第1次建立误差库时完成即可，后续只需构建精细化网格便可完成对误差库的更新，相比于跟踪仪在构建精细化网格的低效率，wMPS总耗时能够再缩减50%以上。综上所述，本文所研究方法可以实现机器人绝对定位误差的高效高精度补偿。

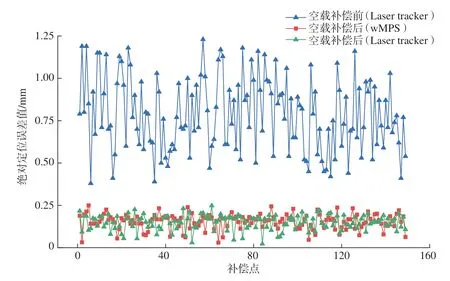
图15 使用wMPS和激光跟踪仪完成绝对定位误差补偿的效果对比Fig.15 Effect comparison of absolute positioning error compensation using wMPS and laser tracker

表2 网格建立效率对比表Table 2 Measurement efficiency comparison table min

4 结论

本文针对机器人在工作空间相邻位置处绝对定位误差矢量显著线性正相关的特点，利用工作空间测量定位系统wMPS高精度动态测量的优势，设计了一种基于空间误差库的机器人绝对定位误差补偿方法，通过对工作空间的网格精细化划分和快速测量，建立并更新空间误差库，在不影响作业节拍情况下实现空间任意点的绝对定位误差矢量预测及补偿。

（1）利用工作空间测量定位系统wMPS测量效率高、覆盖广的优势实现了空间误差库的快速建立及实时更新，为动态变化的机器人定位误差高精度补偿提供了可能。

（2）综合考虑插值精度和效率需求，提出了一种空间网格精细化设计方法，能够确定不同区域定位误差矢量显著线性相关的最大空间距离，并设计最优网格划分策略，从而提高了误差库建立效率。

（3）后续可基于wMPS多目标并行测量特点，设计一种全向靶标解决机器人在运动过程中由于姿态变化导致的光信号遮挡问题，实现工作空间内全位姿实时测量。