随机活动工期下求解资源约束项目最大期望净现值的动态调度算法
2022-07-15白思俊郭云涛
陈 志, 白思俊, 郭云涛
(西北工业大学 管理学院,陕西 西安 710072)
0 引言
项目进度计划是指在项目工作分解结构(Work Breakdown Structure, WBS)的基础上合理安排每个活动的开始、结束时间以满足特定的目标。传统上项目进度计划的主要目标为确保项目能够按时完成,然而对于一些工期要求比较宽松,资金密集型的项目,如何最大化项目的净现值(Net Present Value, NPV)往往成为项目管理者关注的首要目标。项目进度计划显然与项目净现值息息相关:活动的执行需要消耗资源,产生一定的成本,同时项目的支付也往往以特定活动的完成为依据进行,因此伴随着活动的执行,项目会产生一系列正向和负向的现金流。对于活动不同的进度安排将导致活动所产生的现金流发生在不同的时刻,从而会影响整个项目的净现值。传统上,在进行项目进度计划之前,项目管理者会对WBS中的每个活动给予一个期望时间,然后依据此期望时间对项目进行调度,然而现实中项目总是会受到各种不确定因素的影响,如:资源不到位导致活动不能够按计划进行,天气原因使得活动不得不推迟进行等。所以,活动的工期实际上为一随机变量。当活动的工期为一随机变量时,如何对活动进行安排使得项目的期望净现值最大是本文研究的问题。
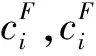
本文在文献[11~13]的基础上考虑了指数分布工期下具有资源约束的折现现金流项目调度问题。对于该问题的优化本文仍采用动态规划算法,但是由于考虑了资源的约束,需要重新设计动态规划算法状态的生成及最优解的求解过程,使得最优解满足资源的约束。与现有文献不同的是本文重新设计了动态规划算法状态的生成过程并对其进行了优化,使得生成的状态既能满足活动之间的逻辑关系及资源的约束,又大大减小了生成重复状态的数量。同时本文分析了不同状态最优目标值之间的关系,使得满足一定条件的多个状态只需要计算一个状态的最优目标值,从而减少了算法的计算时间。最后本文将设计的算法在504个案例上进行了实验,实验结果验证了算法的有效性。
1 问题的描述

(1)
式(1)中γ为折现因子。一般来说项目在完成一些特定的活动V′⊂V后才会得到一笔固定的收入gi>0(i∈V′),其中n+1∈V′,即整个项目结束后会得到一笔固定收入,对于其他活动i∈VV′,gi=0。
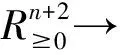
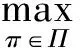
(2)
图1为该问题的一个案例。假设该项目只需要使用一种资源,该资源总的供给量为10个单位。图1中活动上方的数字分别为该活动的期望工期、期望现金流,下方的数字为该活动对资源的需求量。由于活动1和活动2对资源的总需求量超过了该种资源的总供给量,因此活动1和活动2不能同时执行。假设折现因子γ=0.04,可以计算在策略π1={将活动2推迟至活动1结束之后,其他活动在其紧前活动结束的时刻即开始}下该项目的期望净现值为28.599,策略π2={将活动2推迟至活动1结束之后,同时若活动1的结束时间早于时刻6,则将活动3推迟至时刻6再开始,其他活动在其紧前活动结束的时刻即开始}下该项目的期望净现值为32.789,最后在策略π3={将活动1推迟至活动2结束之后,活动3推迟至活动4结束之后,其他活动在其紧前活动结束的时刻即开始}下该项目的期望净现值为51.166。可见不同的调度策略下项目最后的期望净现值是不一样的。可以证明上述3个策略中π3为全局最优调度策略。
2 动态规划算法的设计
由图1所给出的案例可知,通常情况下该问题的求解会比较复杂,由于活动的时间为随机数,而一个活动可以在其所有紧前活动结束后的任意时刻开始,这样单就一个活动来说其解就有无限多种可能性。但当活动时间服从指数分布时,文献[11~13]证明了如下的定理:
定理1当活动时间服从指数分布时,该问题的最优解中每一个活动总是在其他活动结束的时刻开始,即最优策略中每一次决策总是发生在某一活动结束的时刻。
定理1大幅简化了该问题的求解过程,使得该问题的解空间由无穷变为了有限。本节在定理1的基础上针对第2节所描述的问题设计了一种动态规划算法。
2.1 阶段的划分,状态,决策及状态之间的转移
对于含有n+2个活动的项目G,可以将该问题的求解划分为n+2个阶段。其中每一个阶段至少包含1个状态。第m阶段所有状态集合为Sm,第i个状态为Sm,i=(φm,i,φm,i),其中φm,i和φm,i为V的一个子集,即φm,i,φm,i⊆V并且φm,i∩φm,i=Ø。φm,i表示该状态下已经完成的活动,φm,i表示该状态下正在进行的活动。S1,1=({0},Ø)为第一阶段唯一的状态,表示虚拟开始活动被完成,Sn+2,1=(V,Ø)为最后一阶段唯一的状态,表示项目所有活动已经被完成。图2给出了求解图1中问题的阶段及状态,图中圆角矩形表示状态,状态中分号前边的活动集合为φ,分号后边的活动集合为φ,若分号后无活动则表示φ为空。连接不同状态边上的数字表示状态之间转移所采取的决策,如当处于状态S3,1=(0,1,3;)时,若开始活动2则可以到达状态S4,1=(0,1,2,3;)。图中圆形则表示决策之后的状态可能会发生多种不同的情况,如当处于状态S2,2=(0,2;)时,若同时开始活动1和4,则当活动1早于活动4结束时会到达状态S3,5=(0,1,2;4),当活动4早于活动1结束时会到达状态S3,6=(0,2,4;1)。在图1所示的案例中第二阶段省略了状态(0,1;2)和(0,2;1),这两个状态虽然满足逻辑关系,但是由于资源的约束,活动1和活动2不能够同时开始,因此它们为不可行状态。
假设E(S)为当处于状态S时的允许决策集合,E(S)中包含了状态S下可以开始的活动集合,若活动i∈E(S),则活动i的所有紧前活动在状态S时已经被完成,即E(S)={i∈VS|∀(j,i)∈E,j∈φ}。如图1中所示的项目,当活动0,1,2被完成时,可以开始活动3和4,所以E(S3,4)={3,4}。决策变量D(S)表示当处于状态S时实际开始执行的活动集合,显然D(S)⊆E(S)。决策变量的取值应当考虑资源的约束,即同一时刻正在执行的活动对任何一种资源的需求不应当超过该种资源的供给量,即∑i∈D(S)∪φri,k≤Rk,∀k∈ω。对于某一状态S,当φ≠Ø时,E(S)可能为Ø,如图2中E(S3,3)=Ø;当φ=Ø,同时决策变量D(S)=Ø时表示放弃执行该项目剩余的活动,本文所建立的模型并不考虑这一决策变量。
由于最后一个阶段的状态及该状态下的目标值是已知的,因此对该问题的优化需要采用逆推的方式进行。第m-1阶段的所有状态也是由第m阶段的状态生成。当不考虑资源的约束时,对于一个具有m个已完成活动和w个正在执行活动的状态,其满足逻辑关系的前驱状态及相应的决策如图3所示。若当前状态有m个已完成活动,则前一阶段状态必然有m-1个已完成活动,同时前一阶段状态中正在执行活动的个数加上决策集合中的活动个数必然等于w+1。与一个状态的前驱状态相似,一个状态的后继状态个数往往也多于一个,如当|φ|=m-1,|φ|=0,|D(S) |=w+1时,其后继状态就多达w+1个。因此,若对于第m阶段的每一个状态考虑其所有可能的前驱状态则会生成大量重复的状态,使得计算需要大量的时间。为了节省计算时间,同时又不遗漏任何可能的状态,本文设计了一种新的计算方法来计算前一阶段所有满足逻辑关系和资源约束的状态,其计算过程如算法1所示。对第m阶段的状态Sm,i=(φm,i,φm,i)∈Sm,首先计算集合H(Sm,i),H(Sm,i)中包含了那些在第m-1阶段中可以从φm,i中去掉的活动。若活动j在第m-1阶段可以从φm,i中去掉,则活动j的后继活动集合Sucj中的任何活动必然不属于φm,i∪φm,i。对于状态Sm,i=(φm,i,φm,i),若|φm,i|=w≥1则只需要产生|φm-1,j|=w+1的所有满足逻辑关系的状态, 若|φm,i|=0则需要产生|φm-1,j|=0和|φm-1,j|=1的所有满足逻辑关系的前驱状态。定理2保证了算法1能够产生第m-1阶段所有满足逻辑关系的状态。
算法1 计算前一阶段所有满足逻辑关系及资源约束状态的伪代码

Algorithm 1Determine all the states of stage m-1Input: Sm,i(m=1,2,…,n+2),rj,k(j∈V,k∈ω),Rk(k∈ω)1.for every state Sm,i=(ϕm,i,φm,i)∈Sm2.determine H(Sm,i)={j∈ϕm,i|Sucj∩(ϕm,i∪φm,i)=Ø}3.if|H(Sm,i)|>14.move every activity j∈H(Sm,i)from ϕm,ito φm,i, generate new state Sm-1,i′=(ϕm,i-j,φm,i+j)∈Sm-1, check the feasibility of re-source demands5.end if6.if|φm,i|=07.remove every activity j∈H(Sm,i)from ϕm,i, generate new stateSm-1,i′=(ϕm,i-j,Ø)∈Sm-18.end if9.end for
定理2对于第m阶段的状态Sm,i=(φm,i,φm,i)∈Sm,若|φm,i|=w≥1,则只需要产生|φm-1,j|=w+1的所有满足逻辑关系的状态,若|φm,i|=0,则需要产生|φm-1,j|=0和|φm-1,j|=1的所有满足逻辑关系的状态,该过程足以产生第m-1阶段所有满足逻辑关系的状态。
定理2简化了由第m阶段状态产生第m-1阶段所有状态的过程,使得产生重复状态的数量大大减少。
定理3对于任意状态Sm,i=(φm,i,φm,i)∈Sm,|φm,i|=w,活动j∈H(Sm,i),状态Sm-1,i′=(φm,i-j,φm,i+j)满足逻辑关系的充分必要条件是|H(Sm,i)|>1。
对于第m阶段状态Sm,i=(φm,i,φm,i),在计算出H(Sm,i)之后,生成第m-1阶段状态时只需要将H(Sm,i)之中的活动逐个从φm,i中移至φm,i。若|φm,i|=0,则还需要将H(Sm,i)之中的活动逐个从φm,i移除。在将H(Sm,i)之中的活动逐个从φm,i中移至φm,i时还需要考虑资源的约束,若新的状态不满足资源的约束则可以将其直接删除,从而节省程序对存储的需求及计算时间。
推论1对于任意状态Sm,i=(φm,i,φm,i)∈Sm,|φm,i|=w,活动j∈H(Sm,i),状态Sm-1,i′=(φm,i-j,φm,i+j)是满足资源需求的,则必然存在着另一活动j′∈H(Sm,i),满足rj,k+rj′k+∑q∈φm,irq,k≤Rk,∀k∈ω。
推论1是定理3的一个直接结果,由于第m-1阶段状态Sm-1,i′=(φm,i-j,φm,i+j)是第m-2阶段状态Sm-2,i″=(φm-2,i″,φm-2,i″)的后继状态,而状态Sm-2,i″产生Sm-1,i′必须满足条件|φm-2,i″|+|D(Sm-2,i″)|=w+2,即w+2个活动可以同时被执行。
以图2为例,当状态为S4,1时,H(S4,1)={2,3},按照算法1可以生成状态S3,1,S3,2,S3,3,S3,4。当状态为S4,2时,H(S4,2)={3},无需生成任何前驱状态。当状态为S4,3时,H(S4,3)={4},无需生成任何前驱状态。当状态为S4,4时,H(S4,4)={1,4},按照算法1可以生成状态S3,4,S3,5,S3,6,S3,7,其中状态S3,4为重复生成的状态。
2.2 目标函数及最优值函数
当处于状态S时,若以V(S)表示决策D(S)下的目标函数值,则采用逆推的方法可以得到V(S)的表达式如下:
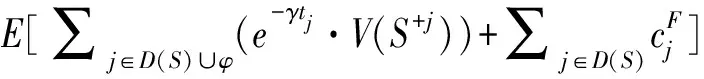
(3)
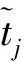
=1-e-t∑j∈D(S)∪φλj=1-e-tρ
(4)
活动j∈D(S)∪φ最先完成的概率为
(5)
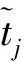
(6)
f(t,j)=λje-t∑i∈D(S)∪φλi=λje-tρ
(7)
则由式(7)计算可得
(8)
最后将式(8)带入式(3)中可以得到V(S)的最终表达式为
(9)
而最优值函数V*(S)的表达式为
V*(S)=maxD(S)⊆E(S)V(S)
(10)
以图2为例,当处于状态S3,4时,允许决策集合E(S3,4)={3,4}。假设V*(S4,1)=187.59,V*(S4,2)=220.59,V*(S4,3)=277.78,V*(S4,4)=166.78,则当D(S3,4)={3}时,后续状态只有S4,1,此时V(S3,4)=62.69,当D(S3,4)={4}时,后续状态只有S4,4,此时V(S3,4)=89.63,当D(S3,4)={4,5}时,则状态S3,4会以9/11的概率转移至状态S4,2,以2/11的概率转移至状态S4,3,此时V(S3,4)=72.80。综上可知V*(S3,4)=89.63,而最优决策D*(S3,4)={4},即当活动0、1、2结束时,只开始活动4,推迟活动3的开始时间。
2.3 最优策略的求解
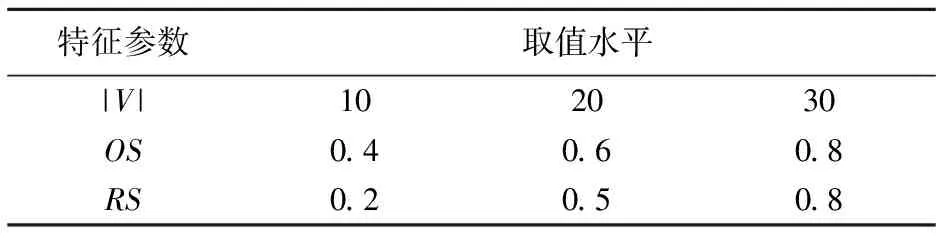
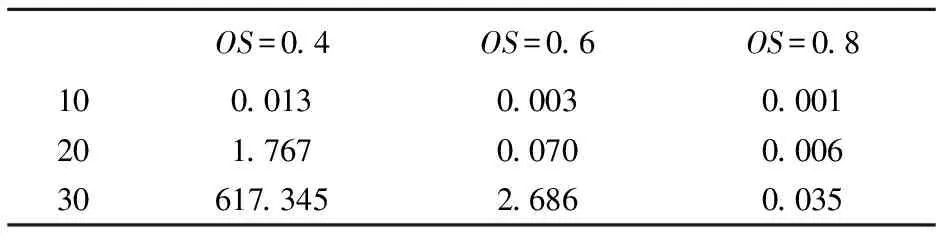
对于每一状态下最优决策的求解为一组合优化问题,该问题与背包问题十分相似,资源的约束为背包容量,活动对资源的需求为物品重量,目标为在资源的约束下最大化状态的净现值。针对该问题本文设计了一种分支算法来求解最优决策。图4给出了一个求解最优决策的案例,图中状态节点右边的数字为该状态的最优目标值,活动上边的数字为期望工期、期望现金流,下边的数字为该活动对资源的需求。4种资源的总供给量为(12,11,10,13)。图5给出了求解图4中问题的分支算法的过程。图5中方框中的数字表示决策变量D(S),有向边上的数字+i表示该状态下的决策包括活动i,相反若有向边上的数字为-i,则表示该状态下的决策不包括活动i。对于状态S,若|E(S)|=m,则该分支树最多有m层。对于第j层节点,若j 算法2求解随机活动工期下资源约束项目最大期望净现值的动态规划算法流程 Algorithm2 Determine the maximum expected NPVInput: G=(V,E),ri,k,cFi,dEi(i∈V,k∈ω)Output: V∗(S1,1)1.Sn+2,1←(V,Ø),V∗(Sn+2,1)←cFn+22.for stage m←from n+2 to 2 do3.based onSm, generate statesSm-14.for state Sm-1,i∈Sm-15.determine the D∗(Sm-1,i)and V∗(Sm-1,i)6.end for7.free memory occupied bySm8.end9.free memory occupied byS1 为了验证算法的有效性,本文对2节设计的动态规划算法利用C++在Microsoft Visual Studio 2017中进行了测试。测试环境为Intel Core i5-2400 4核处理器,3.10 GHz主频及4 GB RAM。 (11) (12) 表1 项目案例参数的取值水平 表2给出了不同活动数量及次序强度下算法求得项目案例最优值所需要的平均时间。总的来说随着项目活动数量的增加,算法所需的时间也在增加;随着项目案例次序强度的增加,算法所需时间在减小。其中项目案例的次序强度对算法所需时间有着较大的影响。表3给出了这一影响的具体原因:对比表3的不同列,会发现项目的次序强度越小,动态规划算法所产生的状态数量越多,由于每个状态均需要计算其最优决策与最优目标值,因此算法需要较长的时间。表4给出了不同项目活动数量下资源强度对案例状态数量的影响,从表中可以看出项目案例的状态数量随着资源强度的增加也在增加。这一现象很好理解,随着可利用资源的增加每一状态S的允许决策集合E(S)中的活动数量也会增加,从而其后续可能的状态数量也会增加,这导致了整个案例状态数量的增加。 表2 不同活动数量及次序强度下项目案例的平均计算时间(s) 表3 不同活动数量及次序强度下项目案例的平均状态数量 表4 资源强度对项目案例状态数量的影响 本文研究了随机活动工期下如何调度资源约束项目使得项目的期望净现值最大化。首先对问题进行了描述和界定,并建立了优化模型。该模型假设项目活动时间为一已知分布的随机变量,项目管理者需要在满足活动逻辑关系和有限资源的约束下对项目调度进行优化,使得项目的期望净现值最大。由于活动时间为不确定的值,项目的调度不再是给出每个活动的开始时间,而是确定一动态调度策略。针对该问题的特点本文设计了一种动态规划算法。在动态规划算法中状态变量和决策变量具有组合属性,随着项目活动的增多,状态空间和决策空间的规模会呈指数级增长,因此如何高效地生成状态并求得状态的最优决策和目标值是算法设计的关键。本文在分析了项目网络图结构的基础上优化了状态的生成过程,使得算法能高效地生成满足活动逻辑关系及资源的约束的状态。同时本文发现了在求解状态最优决策和目标值的过程中满足一定条件的多个状态只需要计算一个状态的最优决策和目标值,从而减少了算法的计算时间。最后,本文将设计的算法在540个不同规模和不同特征的仿真案例上进行了测试,实验结果验证了算法的有效性。同时实验发现:在相同规模的项目之间,次序强度对算法所需时间有着较大的影响,随着项目次序强度的减小,算法生成的状态数量会增加,从而计算时间也会增加。本文给出的动态规划算法只能对活动时间为指数分布的案例进行优化,当项目活动时间为非指数分布时定理1不再成立,因此动态规划算法并不能给出该问题的最优解。如何求解非指数分布工期下项目的最大期望净现值是值得进一步研究的方向。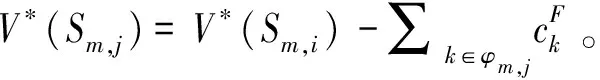
2.4 算法流程
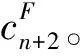

3 实验设计与结果
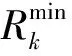


4 结语
