基于流场仿真的导流型鱼礁体组合优化研究
2022-07-15毛海英于定勇王开睿
毛海英,胡 聪,于定勇,王开睿
(1.广西科技大学土木建筑工程学院,广西 柳州 545001;2.山西省第六地质工程勘察院有限公司,山西 运城 044000;3.中国海洋大学工程学院,山东 青岛 266100)
人工鱼礁是人为在海底设置的有效构筑物,为鱼虾等海洋生物营造良好的栖息环境,以达到渔业资源保护和增殖的目的.我国人工鱼礁自20世纪70年代开始试验,目前,辽宁、天津、河北、山东、香港和台湾等沿海地区,都已启动人工鱼礁的规划和建设.
人工鱼礁可净化海水水质环境,改变海水水流方向,形成上升流,有利于鱼类摄食、滞留和聚集,其中流场效应对提高鱼类摄食十分重要.目前,国内外学者对于人工鱼礁的流场效应研究主要有模型实验和计算流体动力学(computational fluid dynamics,CFD)数值计算.模型实验是人工鱼礁水动力学研究的重要方法,可根据实际情况缩小比例尺测得各个工况下的模型参数,实验条件良好,过程直观.随着数值数学与计算机科学的结合,CFD得到迅速发展,已经逐渐应用到了人工鱼礁流场效应分析中.Sanchez-Jerez等[1]和Christopher等[2]通过物理模型实验研究了地中海及新加坡海域人工鱼礁体的集鱼作用.Fujihara等[3]通过数值计算物理-生物耦合模型研究了礁体前方的上升流的变化.借助粒子图像测速PIV试验[4-6],通过改变不同水流速度和人工鱼礁体迎流角度,研究了人工鱼礁体产生的上升流及背涡流的变化规律.不同学者基于CFD研究了立方体框架[7]、米字型[8]、圆台型[9]、三棱体[10]、梯形台[11]等人工鱼礁体对水动力特性的影响.礁体排列方式及布设间距的改变对流场效应影响不容忽视,不同形式人工鱼礁体在不同排列下[12-14]流场效应的差异较大.
本文基于CFD,以导流型鱼礁体为研究对象,验证了数值计算结果的可信度,开展了不同纵横布设间距下的鱼礁体组合优化研究,通过计算上升流最大高度、上升流水平跨度、上升流体积和阻力系数,分析其变化规律及产生原理,选取最优的布设间距,形成最佳流场效应,为人工鱼礁体选型、设计和布设提供科学依据.
1 物模实验
1.1 模型优选及制作
首先进行鱼礁体优选,选型涉及材料、形状、结构、投放及布局等问题,参考人工鱼礁体的优化选型依据文献[15]中的4个参数:礁体体积V(礁体外轮廓线包围体的体积)、礁体表面积与礁体体积之比η(η=礁体表面积/礁体体积)、礁体空方体积与礁体体积之比ε(ε=礁体空方体积/礁体体积)和礁体覆盖区面积A(礁体水体底部所占的水体面积).本文选取方型[16]、梯形[11]和导流方型鱼礁体进行对比(表1).方型和导流方型的礁体体积V比梯型要大,导流方型的η占优,由于附着生物量增多,对增值类鱼礁最有利,梯型和导流方型的ε数值接近,ε的增大可产生较大的流态效应,综上,导流型鱼礁体选型较优于方型和梯型.

表1 不同型式人工鱼礁比较
物模实验中模型比尺取λ=20,导流型人工鱼礁体外表面尺寸为15 cm×15 cm×15 cm,开口比(迎流面开口沿水流垂直方向投影面积与迎流面面积的比值)φ为0.1,上下布设两层导流叶板,导流型叶板厚为1 cm,与竖直方向夹角为45°.生产性鱼礁采用混凝土材料,其中混凝土糙率n实=0.014,根据水力相似准则,λ=20时,n模=n实/λ1/6=0.008 5,有机玻璃较光滑,糙率取值范围为0.007 5~0.008 5,满足试验要求,导流型人工鱼礁体结构如图1所示.
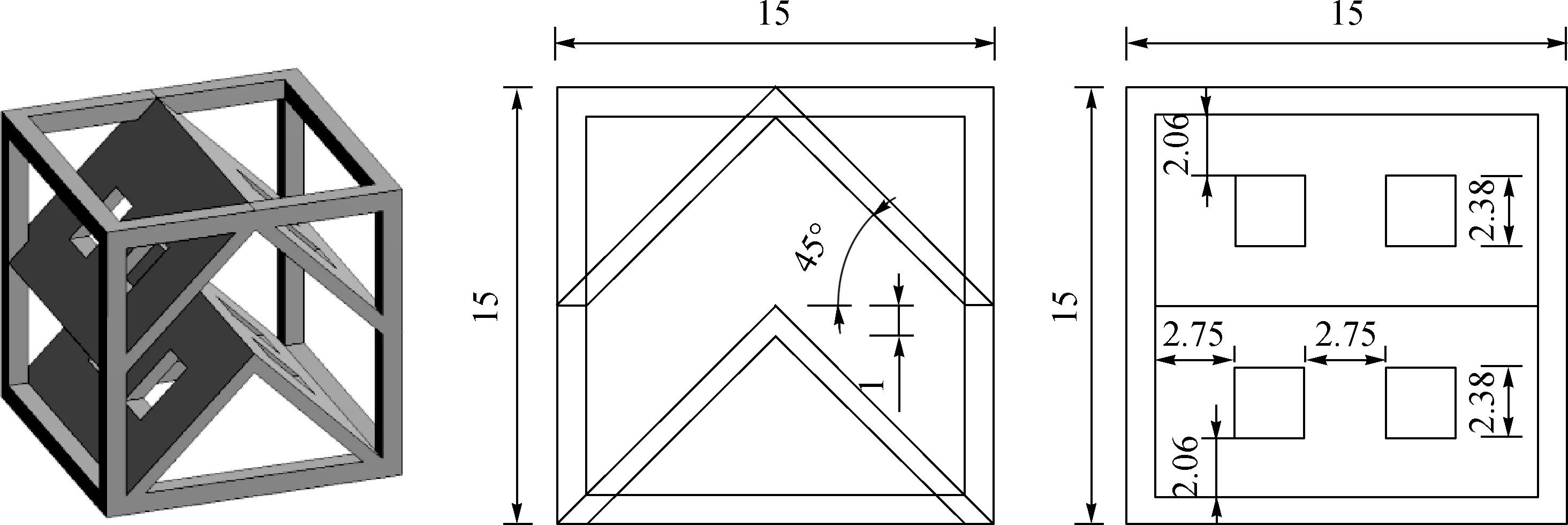
图1 鱼礁体结构尺寸(单位:cm)Fig.1 The structure size of artificial reef (unit:cm)
1.2 实验装置及仪器
流速测量采用Vectrino小威龙点式流速仪,采样体积最小0.085 ml,采样输出频率最高200 Hz,流速范围0~4 m/s,测量点距离中央发射点5 cm,精度为±0.5%,可准确测量礁体前后不同距离的流速.礁体阻力测量采用六分力仪传感器,六分力仪传感器一侧与鱼礁固定,另一侧与水槽上部连接固定,其量程0~50 kg,精度为±0.3%,可准确测量礁体的阻力.
1.3 实验方法
利用螺母将模型固定在直径为10 mm的螺杆上并垂直悬挂在水中,模型底面与水槽底面相接近但不接触,水槽底面作为模拟海底,假设礁体模型底部不受缝隙水流的作用.礁体表面距离水槽自由液面较远时,不考虑自由液面的影响,螺杆另一端与六分力仪相连接.用声学多普勒流速仪(ADV)测量距离礁体模型迎流面前方0.6 m处的流速,待其流速稳定后移动流速仪测量礁体周围测点的流速,每个测点实验3次,每次记录历时10 s的流速数据,然后取其平均值作为该测点的流速测量值,实验装置示意图如图2所示.

图2 模型实验装置示意图Fig.2 Schematic diagram of model test device
根据重力相似准则,模型比尺λ=20,得到礁体模型迎流面前方0.6 m处流速应为0.179 m/s.首先保证礁体前0.6 m处的流速稳定在0.179 m/s,然后测量A1B1(流速测点的坐标)、A2B1、A3B1、A4B1、A5B1、A6B1点的流速,其中S为纵向布设间距.纵向布设间距1.0和2.0倍礁体长度下测点位置见图3.

图3 不同双礁纵向布设间距下测点位置示意图Fig.3 The sketch of measurement points position of double reefs with different spaces
2 数学模型
2.1 控制方程
假定导流型鱼礁体周围的流体特性为黏性不可压缩流体,温度恒定,可忽略能量方程.
连续方程:
(1)
动量方程:
fi,
(2)

2.2 湍流模型
导流型鱼礁体周围流线变化幅度较大,且存在高应变率流动,故采用RNG(Renormalization group model)κ-ε湍流模型,该模型可较好模拟近壁区内Re数较低的流动.
湍动能κ方程:
(3)
湍流耗散率ε方程:
(4)

2.3 鱼礁结构及模拟计算区域
本文研究的导流型人工鱼礁体外表面尺寸为3.0 m×3.0 m×3.0 m,开口比φ为0.1,上下布设两层导流叶板,导流叶板厚为0.2 m,其与竖直方向夹角为45°.导流型鱼礁体横向布设间距分别为0.5L、1.0L、1.5L和2.0L,纵向布设间距分别为0.5L、1.0L、2.0L、3.0L、4.0L和5.0L.来流速度选取0.8 m/s,模型的计算区域见图4.

图4 双礁纵向布设间距3.0L流场计算域(单位:m)Fig.4 Calculation range of flow while double reefs with 3.0L vertical direction (unit:m)
2.4 模型可靠性验证
为消除不同网格大小引起的结果差异,以纵向间距3.0 m为例,网格尺寸分别设置为0.9,0.7,0.5,0.3 和0.2 m,以前方礁体阻力系数趋于稳定为验证依据,计算结果如表2所示.当网格尺寸为0.3 m时,网格单元数为33.84×105个,前方礁体阻力系数趋于稳定值1.293,综合考虑计算效率,选取网格计算尺寸为0.3 m,其收敛性符合要求.

表2 不同网格尺寸验证
为了验证数值计算模型的可靠性,按照物理模型试验条件进行了数值计算.由于横纵向布设的实验条件、数值RNGκ-ε湍流模型均相同,本文仅进行纵向间距1.0L和2.0L双礁体测点流速、前方礁体阻力系数与物理模型试验结果验证,对比结果如图5和表3所示.

表3 前礁体阻力系数Cd的数值模拟值与实验值比较

图5 不同间距测点流速计算值与实验值比较Fig.5 Comparison between calculated and experimental values of flow velocity at measuring points with different spaces
礁体纵向间距为1.0L时,前方测点受到水流扰动较小,A1B1、A2B1、A3B1处流速模拟值与实验值相对误差较小,A4B1处测点距离后礁体位置较近,受到后礁体与实验螺杆的扰动作用较大,测量读数时流速变化范围较大,测量误差为6.5%,随着距离的增加,A5B1、A6B1处流速模拟值与实验值相对误差较小.礁体纵向间距为2.0L时,各点流速相对误差较小,模拟值和实验值吻合较好.
前礁体阻力系数数值模拟值与物模实验值的比较见表3,礁体纵向间距为1.0L时,数值模拟值与物模实验值相对误差为3.64%,由于前礁体与后礁体距离较近,扰流现象较为明显,加上水槽造流电机的振动及实验螺杆的阻力作用,物模实验值比数值模拟值大.当礁体间距增大到2.0L时,后礁体扰流现象有所减轻,物模实验值与数值模拟值接近,相对误差较小,数值模拟值与物模实验值吻合较好.基于上述验证的数值计算模型,针对导流型人工鱼礁体不同纵横布设间距组合下水动力特性进行了更深入的研究.
3 水动力特性研究
3.1 流场形态
流场特性评估选取上升流(垂向速度与来流速度比大于或等于5%)特征参数,本文采用的特征参数包括上升流高度、上升流水平跨度和上升流体积.
图6给出了不同横向布设间距双礁体组合下断面速度云图,左右礁体流速特性对称分布,礁体前方存在一定的缓流区,流速范围0.7~0.8 m/s,左右礁体中间急流区面积与横向布设间距成正比,当横向间距大于1.5L时,急流区趋于稳定.表4给出了不同横向间距上升流特性参数,上升流最大高度、竖向最大速度和阻力系数均与横向布设间距成反比,0.5L时,上升流最大高度达到礁体高度的2.77倍,1.0L时,上升流体积最大,达到627.73 m3.

表4 不同横向间距上升流特性参数
图7给出了不同纵向布设间距双礁体组合下断面速度云图,当纵向间距为0.5L~2.0L时,前方礁体与后方礁体距离较近,前礁体遮流效应明显,双礁体之间区域流速大部分小于0.2 m/s,双礁体顶部影响区域较大且流速大于0.85 m/s;当纵向间距为3.0L~4.0L时,随着礁体距离增大,前礁体对后礁体影响变小,4.0L~5.0L时,前礁体遮流效应减弱并消失,4.0L时达到临界值,后礁体上方上升流影响范围逐渐增大且趋于稳定.表5给出了导流方型和方型不同纵向间距上升流特性参数,导流方型鱼礁体的上升流最大高度比和上升流水平跨度比明显优于方型鱼礁体,纵向布设下上升流最大高度变化较小;上升流水平跨度与布设间距成正比,大于4.0L时,趋于平缓;纵向间距为0.5L~2.0L时,上升流体积增速缓慢,2.0L~4.0L时,上升流体积迅速增大,4.0L~5.0L时,上升流体积趋于平缓,综合上述组合优化研究,当纵向间距为4.0L时,流场效应较好.

表5 不同纵向间距上升流特性参数
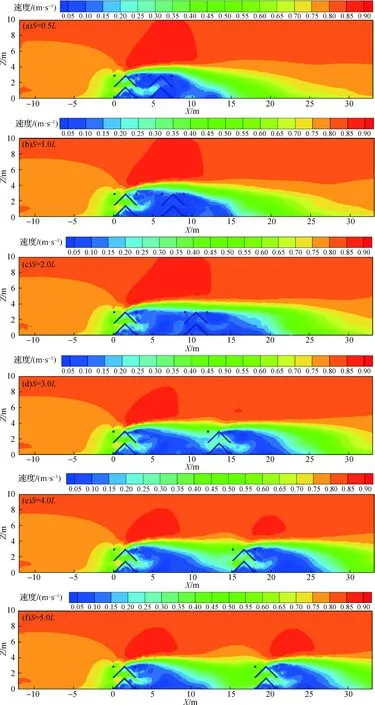
Z表示垂直于XY面方向上的距离.
3.2 阻力系数

(5)



图8 双礁体的kH随S的变化Fig.8 Variation of kH with S of double reefs
纵向排列时,前礁体与后礁体的阻力系数差异较大,前、后礁体的阻力系数与纵向间距成正比,前礁体的阻力系数增幅较缓,2.0L时,后礁体的阻力系数随纵向间距的增大迅速增大,5.0L时,后礁体阻力系数已达到1.023,接近单礁体的阻力系数1.362,当双礁体间距大于4.0L时,后礁体受前礁体遮流效应逐渐减弱(图9).

图9 双礁体的Cd随S的变化Fig.9 Variation of Cd with S of double reefs
4 结 论
本文参考人工鱼礁体的优化选型依据,选取方型、梯形和导流方型鱼礁体进行优化选型,经过不同型式V、η、ε和A的对比,导流型鱼礁体选型较优于方型和梯型.
数值计算并验证了物理模型实验中各个测点的流速值及阻力值,数值模拟值与物模实验值吻合较好,说明数模计算方法可行,结果可信.本文计算了不同横向间距及纵向间距组合下的水动力特性,布设间距不同时,水动力特性差异较大,通过组合优化研究得到如下结论:
1) 随着横向布设间距的增大,上升流最大高度和竖向最大速度减小,上升流体积先增大后减小,0.5L时,上升流最大高度达到最大,1.0L时,上升流体积达到最大;
2) 随着横向布设间距的增大,平均阻力系数和横向阻力影响系数均逐渐减小,表明双礁体阻力系数受横向布设间距的影响逐渐减弱;
3) 随着纵向布设间距的增大,上升流最大高度变化幅值较小,上升流水平跨度和上升流体积与布设间距成正比,大于4.0L时,趋于平缓;随着纵向布设间距的增大,前礁体阻力系数缓慢增大,后礁体阻力系数迅速增大,当间距为4.0L时,后方礁体阻力系数趋于平缓,表明后礁体受前礁体遮流效应逐渐减弱.
根据以上不同纵横布设间距组合优化研究表明,当横向布设间距为0.5L~1.0L、纵向布设间距为4.0L时,导流型人工鱼礁周围的流场效应较好.该研究结果可为礁区布局方案的确定提供参考.
