Laplace变换在第一类高振荡 Volterra方程求解中的应用
2022-07-14严睿琪陈松良
严睿琪,李 斌,王 佩,陈松良
(贵州师范学院数学与大数据学院,贵州 贵阳 550018)
0 引言
卷积形式的积分方程在物理和工程等领域有许多的应用,如在散射问题中合成积分方程是卷积型的[1]。在物理学、工程学等众多领域的积分方程中常含有双曲函数[2]。在这篇文章里,我们主要研究带贝塞尔高振荡核函数和双曲函数的第一类Volterra积分方程
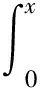
(1.1)
的解,这里f(x)为光滑的函数,f(0)=0,y(x)为未知函数,Jv(wx)为第一类贝塞尔函数,v>-1,w,r为振动参数。
最近关于Volterra积分方程的求解问题的文献较多[3-4],但对于方程(1.1)而言,最显著的特点就是含有高振荡性,当w,r≫1时,核函数将变得高振荡,标准的配置方法和不连续的Galerkin方法无法有效的计算,因为与空间网格相关的长度尺度过小,导致得到的是一个大规模的病态线性系统[5]。而Laplace变换法是计算第一类Volterra积分方程的有效方法,特别是对卷积形式的积分方程有效。2007年,Rahman[6]比较系统的介绍了通过Laplace变换计算各类Volterra积分方程的方法;2014年,向[3]使用Laplace变换和Laplace逆变换来求解带高振荡贝塞尔核函数的沃尔特拉积分方程
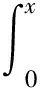
(1.2)
这里w≫1,v为非负整数,f(x)为光滑的函数。大多数情况下,这类方程的解不能以封闭形式解析求解,只能写成高振荡积分解的形式。2018年, Uddin M[7]通过Laplace变换的应用,将积分方程(1.2)转化为代数方程,然后利用Laplace逆变换的方法,将解表示为沿延伸到复平面左半部分的光滑曲线的积分,再求积分。2019年,李[8]等考虑来自电磁与声散射问题,例如平面波是空间时谐波,通过Laplace变换来求解两端带高振荡核函数的第一类Volterra积分方程
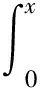
(1.3)
并通过克伦肖·柯蒂斯型方法求出方程的高精度近似解。本文的所有数值结果都是在台式机上用Matlab R2014a实现的(8gb内存,2个2.50 GHz的处理器,Windows 10操作系统)。
1 多项式逼近
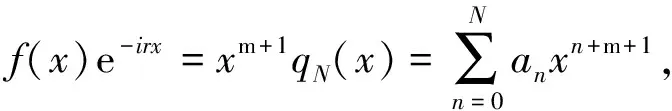
例1设方程(1.3)中f(x)=x2sin(x),r=1000,m=0,则|f(x)e-irx-xm+1qN(x)|和|f(x)-xm+1qN(x)|在x=0.4处的误差分别为表1和表2所示。

表1 例1中f(x)e-irx-xm+1qN(x)在x=0.4处的绝对误差

表2 例1中f(x)-xm+1qN(x)在x=0.4处的绝对误差


称为函数f(t)的Laplace变换,这里的逆Laplace变换记为
2 方程(1.1)的精确解
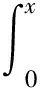
(2.1)
将(2.1)的解yN(x)作为方程(1.1)的近似解,然后令N→∞,则得到方程(1.1)的精确解y(x).
引理1[8]定义m=「ν⎤为小于或等于ν的最小整数,若f(x)∈Cm+1[0,1],m是非负整数,则(1.3)有唯一解y(x)∈C[0,1]的充要条件是
f(0)=f′(0)=…=f(m)(0)=0.

定理1假设f(x)∈Cm+1[0,1],v0=m-ν,f(0)=f′(0)=…=f(m)(0)=0,则方程(1.1)的解可以表示为:
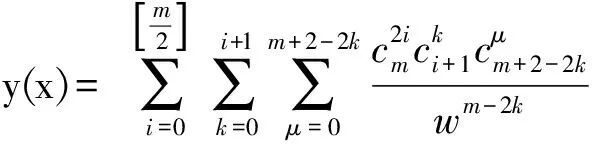
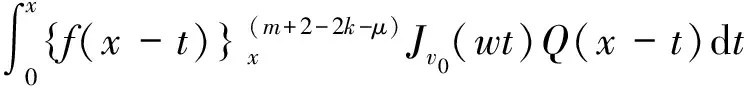
(2.2)
这里
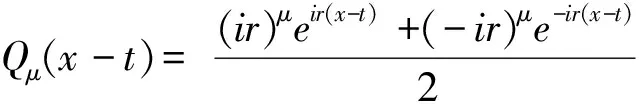
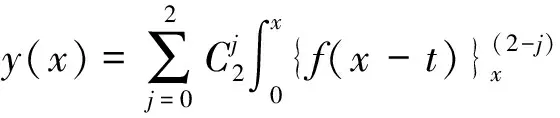
(2.3)
证明(1)方程(2.1)是有卷积形式的积分方程,两边同时采用Laplace变换有
L[yN(x)]
这里
由于L1,L2类似,若算出其中一个,就可得到另外一个。下面先考虑L2的Laplace变换。

则有
这里ν=m-ν0,ν0≥0.下面讨论上面最后一个等式中的第二个和式
则有
接下来考虑Laplace逆变换,上式结合下面的式子(见[10])
(2.4)
(2.5)
=w-δJδ(wx),δ>-1,
(2.6)
δ>0,
(2.7)
可得
根据下面的Laplace逆变换公式
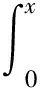
(2.8)
易得
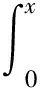
同理,可得关于L1的逆Laplace变换计算公式
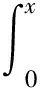
从而得到了方程(2.1)的精确解为
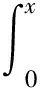
(2)当ν∈Z+,m=ν≠0时,ν0=0,下面考虑m=ν=0时方程(1.1)的解。
这里
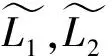

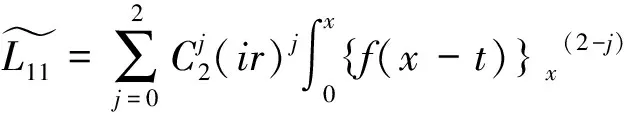

从而得到方程(2.1)的解为
3 数值计算
例2求Volterra积分方程
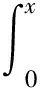
的解,这里f(0)=f'(0)=0.
解由于v=0.2,则m=1,v0=0.8, 结合公式(2.3)可得方程的解为
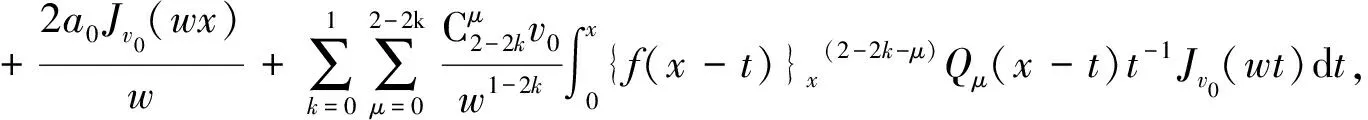
例3求Volterra积分方程
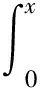
的解,这里f(x)为连续函数,且满足f(0)=0.
解由于v=0, 结合公式(1.4)可得方程的解为

(3.1)
这里
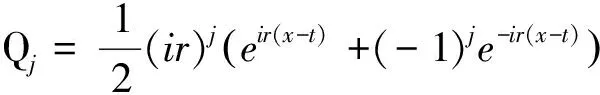
例4求Volterra积分方程
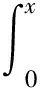
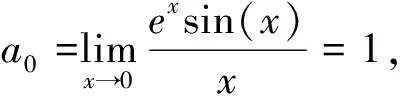

通过Laplace变换得到积分方程积分形式的精确解,这些解的形式为

(3.2)
其中f(x)在区间[0,1]上是连续函数。
如果需要Volterra积分方程的高精度数值解,可通过克伦肖·柯蒂斯型方法[11]计算得到在不同x处的高精度近似解(如表3所示),其误差如图1和图2所示,误差分析为下面的定理2。
定理2[11]采用克伦肖·柯蒂斯型方法计算积分(3.2)可得到如下的误差:
(1)若f在伯恩斯坦椭圆Eρ上是分析性,则I[f]-QN[f]=O(ρ-N);
(2)如果f,f',…,f(m-1)在区间[0,1]上是绝对连续的,且Var(f(m))<∞,则I[f]-QN[f]=O(N-m).

表3 例题4中,当r=1000时,由克伦肖·柯蒂斯型方法[11]在不同的x,w处得到的误差

图1 数值解的误差分析图
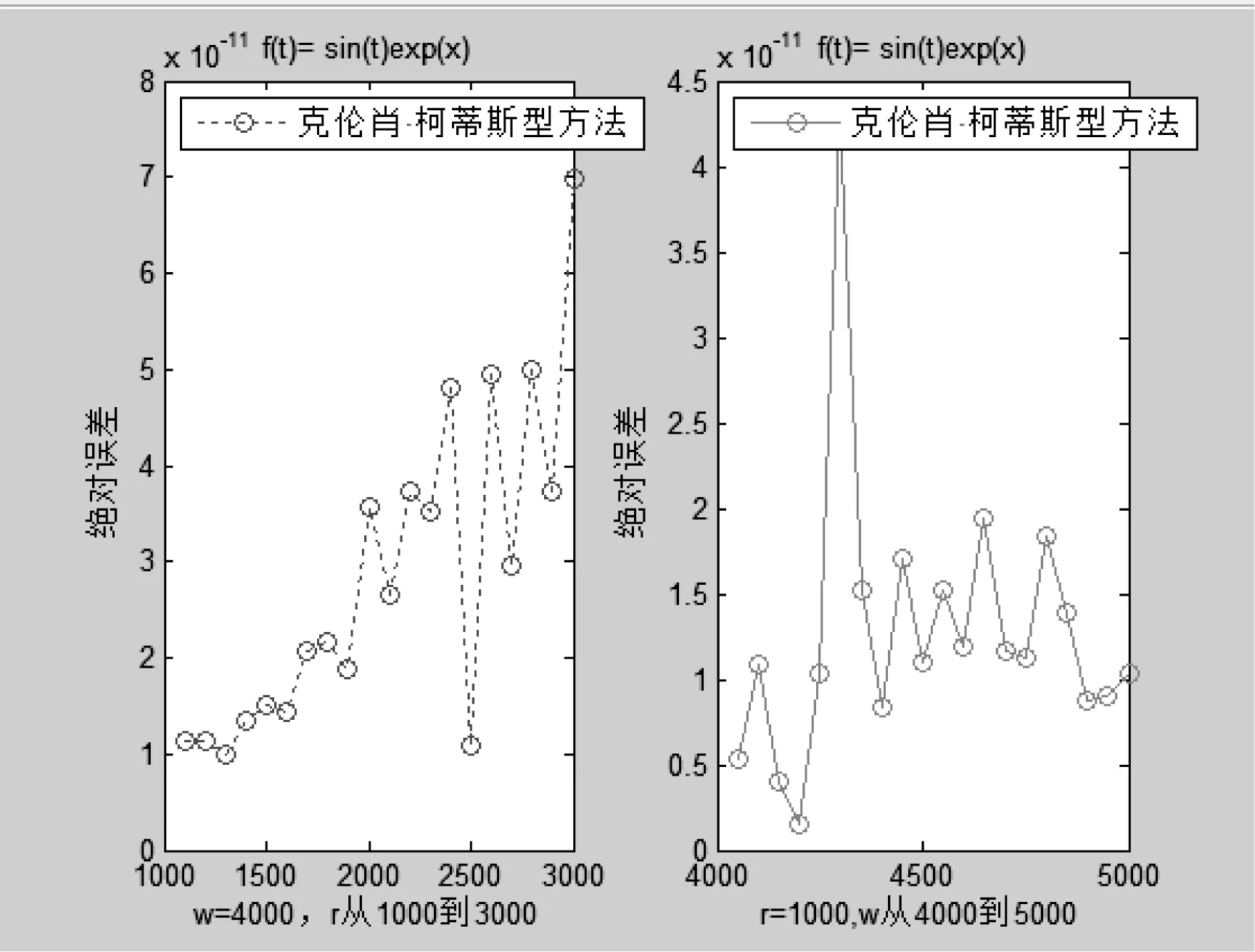
图2 数值解绝对误差分析图
4 结束语