一类圆锥曲线定点问题的解法探究与拓展

汪红毅

(广东省佛山市顺德区乐从中学，528315)

一、问题呈现

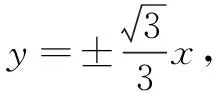
(1)求曲线C的方程;

(2)设点Q(1,0),直线x=t(t∈R)不经过点P且与C相交于A,B两点,若直线BQ与C交于另一点D,求证:直线AD过定点(如图1).

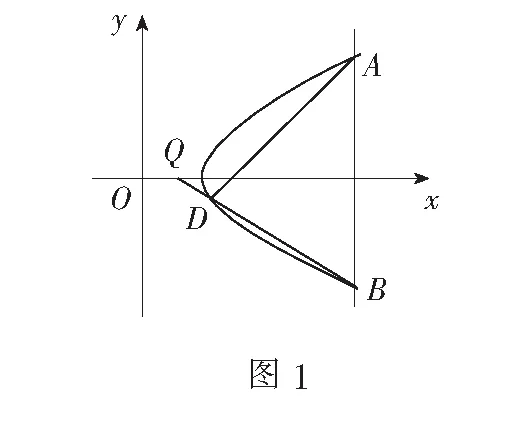
二、解法探究

第(1)问易知答案为x2-3y2=3.

第(2)问的求解条件之一是过定点Q(1,0)的直线QB与双曲线相交,涉及到联立方程组的计算和韦达定理的应用;条件之二是涉及到其中一个交点B的对称点A与另一个交点D的连线问题,弄清楚这三个点的坐标之间的关系,综合以上条件和分析才能得到正确答案.

步骤1寻找A,B,D三点之间的联系

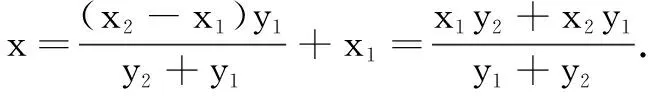
步骤2设直线QB的方程,运用韦达定理求解.

解法1(设点斜式方程)

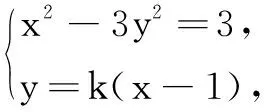
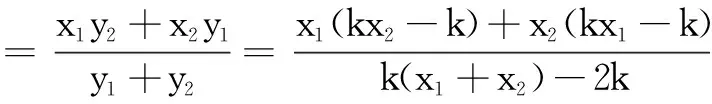
所以直线AD恒过定点(3,0).

解法2(设横截距式方程)

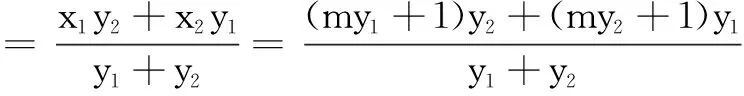
=3.

所以直线AD恒过定点(3,0).

三、关联问题

上述问题和如下的2018年全国高考题有很大的关联.

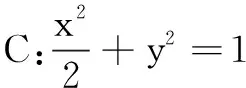
(1)当l与x轴垂直时,求直线AM的方程;

(2)设O为坐标原点,证明∠OMA=∠OMB(如图2).

分析第(2)问中直线l过焦点,证明∠OMA=∠OMB的方法有很多,由于椭圆的对称性,其中一个证明方法可以是反过来证明点A关于x轴的对称点D与点B的连线恒过点M.符合过某一定点的直线与圆锥曲线相交时其中一个交点与另一个交点的连线恒过另外一个定点的特征.

类似的题还有例2所示的2021年广东省肇庆市检测题.

例2已知抛物线C:y2=4x的焦点为F,直线l与抛物线C交于A,B两点,O是坐标原点.

(1)若直线l过点F且|AB|=8,求直线l的方程;

(2)已知点E(-2,0),若不过点E的直线l不与坐标轴垂直,且∠AEO=∠BEO,证明:直线l过定点.

分析第(2)问中已知∠AEO=∠BEO,可以得到点A关于x轴的对称点D与E,B三点共线,即直线ED与抛物线相交于B,D两点,只需证明直线AB恒过定点即可.

四、拓展延伸

对比例1和例2,可以发现他们具有类似的条件与结论,可以试着探究圆锥曲线这一类问题是否都能成立.

结论1假设焦点在x轴的椭圆或双曲线C的方程为Ax2+By2=1(AB≠0),过定点Q(n,0)(定点Q不为原点和曲线C的顶点)的直线l与曲线C相交于D,E两点,点D关于x轴的对称点为F,证明直线EF恒过定点.

证明设直线l的方程为x=my+n,点D(x1,y1),E(x2,y2),则点F(x1,-y1).

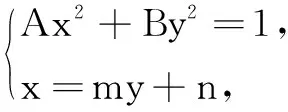
同文首问题的步骤1,可知

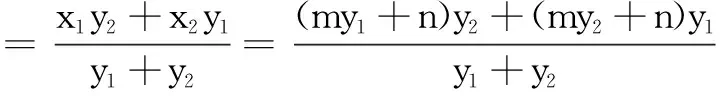
结论2已知过点(n,0)(n≠0)的直线l与抛物线C:y2=2px相交于A,B两点,点A关于x轴的对称点为D,证明直线BD恒过定点.

证明设直线l的方程为x=my+n,点A(x1,y1),B(x2,y2),则点D(x1,-y1).

y1+y2=2pm,y1y2=-2pn.

同上述步骤1,可知

所以直线AB恒过定点(-n,0).

评注根据结论2,我们可验证上述例2的结果是否成立.事实上,设点A关于x轴的对称点为C,由∠AEO=∠BEO,可知点E,B,C三点共线.又点E(-2,0),则直线AB恒过定点(2,0).

综合结论1与结论2,可得

结论3过圆锥曲线对称轴上任意一点作两条关于对称轴对称的直线与该圆锥曲线相交于4个点,分别连结对称轴同侧的4个点得到两条直线,则此两条直线交于定点.

评注由于圆锥曲线的对称性,焦点在y轴上的圆锥曲线也有类似的结论.