利用阿基米德三角形的性质求解面积问题*
2022-07-14唐义恒王安国
唐义恒 王安国 陈 亮
(重庆市合川中学,401520) (重庆市合川区教育科学研究所,401520)
抛物线的弦与过弦的端点的两条切线所围成的三角形称为阿基米德三角形,它具有许多有趣的性质.在近几年的高考试题中,多次出现涉及阿基米德三角形的面积问题.本文以抛物线x2=2py(p>0)为例,阐述如何利用阿基米德三角形的两个基本性质求解相应问题.
一、性质与面积公式
性质1阿基米德三角形底边上的中线平行(或重合)于抛物线的对称轴.
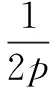
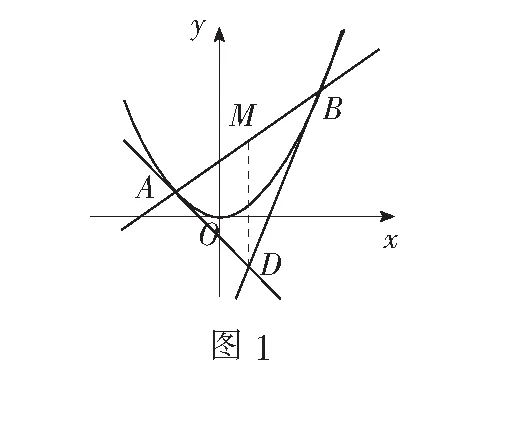
证明如图1,设点A(x1,y1),B(x2,y2)在抛物线x2=2py(p>0)上,弦AB为阿基米德三角形的底边,M为底边AB的中点,D为两切线DA,DB的交点.
易知过点A,B的切线方程分别为
x1x=p(y+y1),
①
x2x=p(y+y2).
②
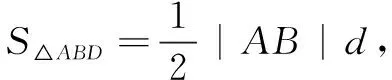

下面利用该结论求解阿基米德三角形面积问题.
二、真题解答


(1)证明:直线AB过定点;

解(1)略.


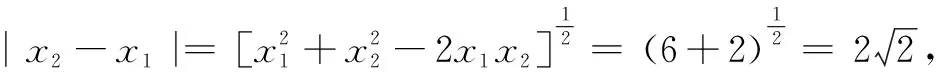


例2(2021年全国高考题)己知抛物线C:x2=2py(p>0)的焦点为F,且点F与圆M:x2+(y+4)2=1上点的距离的最小值为4.
(1)求p;
(2)若点P在圆M上,PA,PB是C的两条切线,A,B是切点,求∆PAB面积的最大值.

解(1)p=2.(过程略)


评注以上两道试题求解的关键在于用两切线横坐标的和与积去衔接阿基米德三角形面积公式.这样的思路不但可以避免求两切点所在的直线方程、点到直线的距离及弦长,还能减少运算,提高解题速度.
三、变式拓展
变式已知抛物线C:x2=4y,PA,PB为C的切线,切点为A,B.
(1)若点P在直线y=x-3上,求∆PAB面积的最小值;
(2)若点P在双曲线y2-x2=1的下支上,求∆PAB面积的最小值.
解设点P(x0,y0),A(x1,y1),B(x2,y2),则x1+x2=2x0,x1x2=4y0.
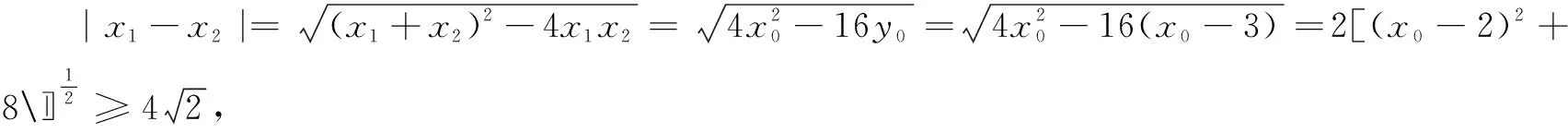


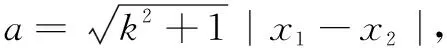
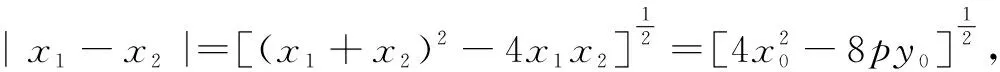
与此同时,我们也能感受到,恰当使用阿基米德三角形的性质能简化运算过程,减少运算量,可以使一些较难的问题得到比较方便的解决,从而提高解题速度和准确度.当然,阿基米德三角形中还隐藏有其他有趣的性质,等待着同学们去探究去发现.
