由特殊到一般——一道试题解答引发的思考

费曙光 何拓程

(北京市通州区运河中学,101121) (北京理工大学附属中学,101119)

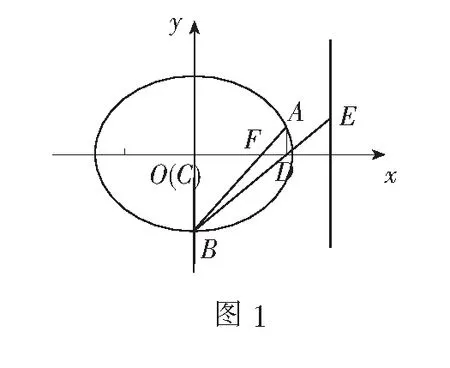
一、问题呈现

(1)求椭圆M的方程;

(2)过点F的直线l与椭圆M交于A,B两点,BC⊥x轴于点C,AD⊥x轴于点D,直线BD交直线x=4于点E,求∆ECD与∆EAB的面积之比.

二、解法探究

1.以静制动,特殊化探路

2.重点突破,一般性论证

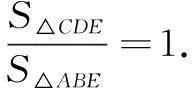
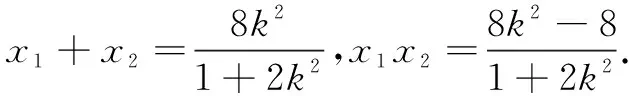
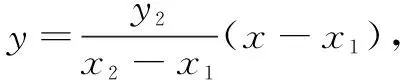
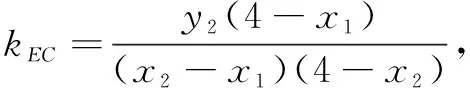
=0,

故C,A,E三点共线.

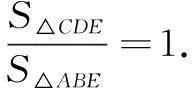
解法2设点A(x1,y1),B(x2,y2),C(x2,0),D(x1,0),同解法1证得C，A，E三点共线.

评注解法1和解法2立足于斜率证明C,A,E三点共线,思维方向是执因索果.我们也可以逆向思维,用同一法证明C,A,E三点共线.

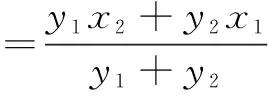
=4.

所以直线AC与BD交点的轨迹方程为x=4,即C,A,E三点共线.

三、背景溯源

回顾第(2)问的上述三种解法,可以发现C,A,E三点共线是隐藏在题设背后的一个重要的隐含条件,是解决问题的关键.注意到x=4为题设椭圆的右准线,由解法3进一步研究,不难发现C,A,E三点共线实质上源于以下一般性结论.

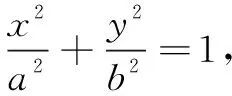
①

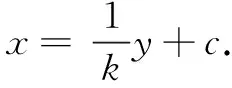
四、感悟

最新出台的高考评价体系提出了基础性、综合性、应用性、创新性的“四翼”要求，其中综合素质的培养要求学生对不同层面的知识、能力、素养能够纵向融会贯通，合理组织和调动相关知识及能力，高质量应对复杂问题情境.通过以上问题的讨论不难发现,当我们在问题求解遇到困难时,不妨先从简单、特殊情形入手,挖掘问题的隐含条件,经历直观、猜想等思维过程,明确一般情形下解题的重点与难点,再围绕重点寻找相关的数学模型与常见处理手段,关联相应知识点,加深数学不同模块的相互联系,使知识与方法有效结合,达成问题的解答.