基于隶属度的模糊加权k 近质心近邻算法

刘利，张德生，肖燕婷

（西安理工大学 理学院，西安 710054）

0 概述

分类任务［1］是利用已知类别的样本通过建立模型预测新样本的类别［2］。分类是数据挖掘中最重要的任务之一，应用十分广泛。目前，常用的分类算法主要有决策树［3］、贝叶斯分类器［4］、人工神经网络［5］、支持向量机［6］、k 近邻（k-Nearest Neighbor，KNN）算法［7］等。这些已有的分类算法及其改进算法被广泛地应用于各个领域，如统计学［8］、医学［9］、模式识别［10］、决策理论［11］等。KNN 算法的基本思想［12］是通过已知类别的训练样本寻找待测样本的k个近邻，将k个近邻中出现频率最高的类别作为待测样本的类别。由于KNN 算法具有理论简单、易于操作等优点，被认为是数据挖掘中最简单的方法之一［13］。但是，KNN 算法也存在不足：第1 个问题是它没有考虑样本的分布，当样本分布不均匀或样本中存在噪声样本时，分类精度会明显下降；第2 个问题是所有训练样本具有同等重要性，判断待分类样本的类别时没有考虑k个近邻的区别；第3 个问题是使用单一的多数投票原则进行分类决策。以上3 个问题都会影响分类的准确率及效率。

针对KNN 算法存在的问题，很多研究者提出了不同的改进算法。文献［14］提出了k 近质心近邻（k-Nearest Centroid Neighbor，KNCN）算法，该算法的设计思想是近邻点要尽可能地离待分类样本近，而且近邻点要均匀地分布在待分类样本周围，通过这些近邻点所属类别判断待测样本的类别。文献［15］提出了一种基于局部权重的k 近质心近邻算法LMKNCN，该算法的设计思想是为k个近质心近邻赋予不同的权重，再通过决策函数对每个测试样本进行分类。文献［16］将模糊理论与KNN 相结合，提出了模糊k 近邻（Fuzzy k-Nearest Neighbor，FKNN）算法，该算法的基本思想是为训练样本分配隶属度，根据k个近邻样本的隶属度和距离的权重，通过最大隶属度原则确定待分类样本的类别。文献［17］提出了自适应k值的FKNN 算法，该算法的设计思想是通过改进的粒子群算法自适应优化k值和模糊强度参数m，从而提高算法性能。文献［18］将KNCN 算法和FKNN 算法相结合，提出了模糊k 近质心近邻（Fuzzy KNCN，FKNCN）算法，该算法的设计思想是使用近质心近邻的概念来确定最近邻，并使用模糊理论为每个类分配隶属度，同时解决了样本分布和权重问题。文献［19］提出了基于Bonferroni 均值的FKNCN 算法，该算法的设计思想是运用均值算子和近质心近邻概念，计算最近的局部Bonferroni 均值向量确定待分类样本的类别标签，该算法对异常值具有很好的鲁棒性。

然而，上述FKNCN 算法及其改进算法在计算训练样本的隶属度时没有考虑训练样本中存在的噪声点或离群点，这在小样本数据集中会大幅降低分类精度。同时，算法忽略了训练样本特征的差异性，没有进行特征选择，影响了分类性能。针对这2 个问题，本文对FKNCN 算法进行改进，提出基于隶属度的模糊加权k 近质心近邻算法MRFKNCN。设计新的隶属度函数计算训练样本的隶属度，区分训练样本中存在的噪声或离群样本与有效样本。在此基础上，通过基于冗余分析的Relief-F 算法计算每个特征的权重，删去较小权重所对应的特征和冗余特征，选出重要特征后根据加权欧氏距离选取k个有代表性的近质心近邻，并确定待测样本的类标号。

1 预备知识

1.1 符号说明

本文算法所使用的符号说明见表1。

表1 符号说明Table 1 Symbol description

1.2 FKNCN 算法

假定在p维特征空间中，训练样本集T=有M个类标签c1,c2,…,cM，给定一个待测样本点y，FKNCN 算法步骤如下：

步骤1利用式（1）计算待测样本y与所有训练样本间的欧氏距离，进行升序排列，选择最短距离所对应的训练样本作为第1 个近质心近邻点

步骤2当r=2,3,…,k时，利用式（2）计算T（iTi表示除去被选为近质心近邻的训练样本之外所有剩余的训练样本）中的训练样本与之前所选的r-1 个近质心近邻的质心：

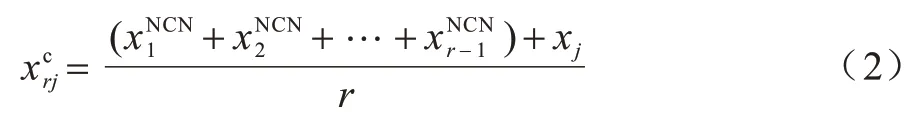
步骤3利用式（3）计算训练样本的质心与待测样本间的最短距离，选取所对应的训练样本作为第r个近质心近邻：

利用式（5）和式（6）均可计算训练样本的隶属度。一般而言，优先选择式（6）计算其隶属度［18］，原因在于该计算方式引入了模糊理论，将训练样本的隶属度模糊化，通过训练样本的k个近邻确定其隶属度，能够确保训练样本在自己的类中被赋予较高的权重，而在其他类中被赋予较低的权重。

步骤5通过最大的模糊隶属度值判断待测样本y的所属类别，如式（7）所示：

步骤6对于一个新的待测样本点，重复步骤1～步骤5。

1.3 特征的相关性度量

定义1皮尔逊相关系数［20］

设p维空间中的2 个样本点e=(e1,e2,…,ep)，f=(f1,f2,…,fp)，两者之间的皮尔逊相关系数的计算公式如式（8）所示：

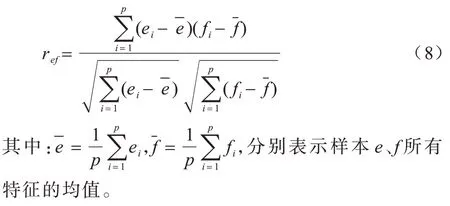
ref表示特征之间的线性相关性，其取值范围是[-1,1]，即0 ≤|ref| ≤1，相关系数的绝对值越大，相关性越强，相关系数的绝对值越接近于0，相关度越弱。

2 MRFKNCN 算法

隶属度函数的设计是FKNCN 算法的关键，但FKNCN 算法在计算训练样本的隶属度时，并没有考虑噪声点或离群点对分类的影响，同时该算法在计算待测样本与训练样本间的欧氏距离时，把所有训练样本的各维特征等同对待，没有区分它们的重要程度，这些都会影响分类的性能。为此，本文提出基于隶属度的模糊加权k 近质心近邻算法MRFKNCN。通过密度聚类思想为训练样本设计新的隶属度函数、利用基于冗余分析的Relief-F 算法计算特征的权重、确定待测样本的类别这3 个部分克服噪声点、离群点的影响，同时解决相同特征权重的问题，提高分类的效率和准确率。

2.1 隶属度函数构造

样本集中经常会出现噪声点或离群点，而FKNCN算法在计算训练样本的隶属度时，没有区分这些样本与有效样本，导致所有训练样本的隶属度相同，这会在很大程度上影响分类的准确率。本文采用密度聚类的思想构造最小包围球。首先计算最小包围球的类中心和半径；然后根据训练样本在最小包围球的位置确定其隶属度；最后根据隶属度的大小判断训练样本是离群或噪声样本还是有效样本。计算最小包围球类中心和半径的具体步骤如下：

步骤1计算训练样本xj与训练样本集中其他样本的欧氏距离，找到xj的第r个近邻(xjr,r=1,2,…,k)。

步骤2根据样本xj的k个近邻构造n×k的密度矩阵D=(d(xj,xjr))n×k。

步骤3利用式（9）计算所有样本的密度ρ(xj)：

步骤4选择最大密度样本点xmax，并找出离该点最近的样本点xn_max，通过这2 个点确定最小包围球的类中心O(T)：

步骤5利用式（10）计算最小包围球的半径：

其中：λ为自定义的惩罚因子；δ为半径调整系数；a(T)为类中心到所有样本点距离的平均值。

计算出样本集中最小包围球的类中心和半径后，利用式（12）确定训练样本的隶属度：

其中：d(xj)为训练样本xj与最小包围球类中心O(T)的欧氏距离。从式（12）可以看出，训练样本离最小包围球的类中心越远，该训练样本的隶属度就越小。如果训练样本位于最小包围球之内，其隶属度都大于0.3；反之，位于最小包围球之外的训练样本，其隶属度都小于等于0.3。位于最小包围球之外的样本一般都为离群或噪声样本。本文构造最小包围球方法简单有效，原因在于其只需计算最小包围球的类中心和半径，再通过式（12）为离群或噪声样本赋予较小的隶属度，即可快速区分出离群或噪声样本与有效样本。

2.2 基于冗余分析的Relief-F 算法

本节提出基于冗余分析的Relief-F 特征选择算法计算每个特征的权重。首先将FKNCN 算法中的欧氏距离改为特征加权的欧氏距离；然后通过加权欧氏距离确定待测样本的近质心近邻；最后通过近质心近邻的隶属度和距离加权确定待测样本的类隶属度。

2.2.1 特征权重的计算

在分类过程中，并不是所有的特征都与分类强相关，也会存在一些不相关特征及冗余特征。如果在分类时不处理这些特征，会出现计算成本高、分类性能低等问题。为了得到最优特征子集，特征选择是必不可少的。Relief-F 算法［21］是最成功的特征选择方法之一，算法的具体步骤如下：

1）对所有特征归一化处理：

2）从训练集中随机选择样本点xj，找出xj同类的k个最近邻样本集和不同类的k个样本集。

3）通过式（14）计算每个特征的特征权重［22］：

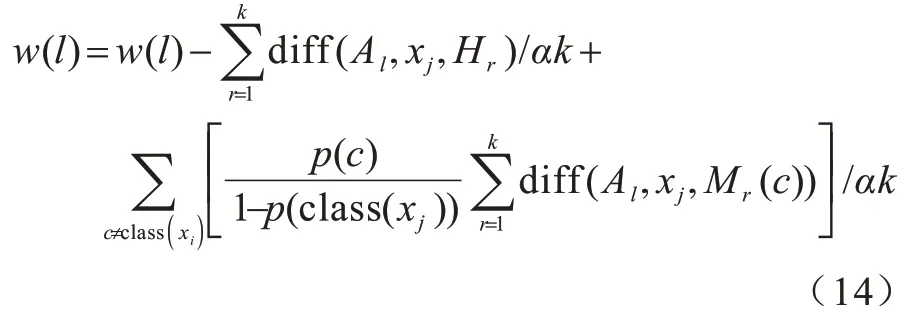
其中：diff(Al,xj,Hr)表示样本xj与Hr在第l个特征上的距离；diff(Al,xj,Mr(c))表示样本xj与Mr(c) 在第l个特征上的距离；p(c)表示属于类别c的样本出现的概率。

虽然Relief-F 算法在处理多分类问题时效率高并且能够很好地剔除不相关特征，但不能过滤冗余特征。为此，本文在Relief-F 算法的基础上提出基于冗余分析的Relief-F 特征选择算法计算所有特征的权重，算法描述如下：

算法1基于冗余分析的Relief-F 算法

输入训练集T，样本抽样次数α，最近邻样本个数k

输出每个特征的特征权重w

步骤1所有特征归一化处理。

步骤2将所有特征权重置0。

步骤3在T中随机选择样本点xj。

步骤4找到与xj同类的k个最近邻样本集Hr。

步骤5每个类c≠class(xj)，找到与xj不同类的k个最近邻样本集Mr(c)。

步骤6更新每个特征的特征权重。

步骤7根据特征权重阈值，选择分类权重最大的特征集合。

步骤8冗余分析。利用皮尔森相关系数计算特征之间的相关性。

以上步骤是在一次抽样下计算每个特征的特征权重，经过α次抽样后，将特征权重更新α次，并设置一个特征权重阈值Γ，将每个特征权重与总特征权重的比值累积，选择累积特征权重比大于阈值Γ的特征作为新特征，并删掉剩余的不相关特征，然后分析新特征之间的相关性，在特征相关性较大的情况下保留权重较高的特征，消除权重较低的特征，目的是消除冗余特征的干扰。通过基于冗余分析的Relief-F 算法计算特征权重，同时减少特征的数量、降低维数，从而完成特征选择。

2.2.2 加权欧氏距离的计算

利用式（15）计算待测样本y与训练样本xj的加权欧氏距离，从而确定待测样本的k个近质心近邻：

2.2.3 待分类样本类别的确定

计算出每个特征的特征权重后，利用式（16）计算待测样本y属于每个类别的隶属度值：

得到待测样本y属于每个类别的隶属度后，通过最大隶属度原则确定待测样本y的类别。

2.3 算法描述

MRFKNCN 算法的设计思想为：首先计算训练样本的隶属度；然后计算所有特征的权重，并找出k个近质心近邻；最后计算待测样本的模糊隶属度，通过最大隶属度原则确定待测样本的类别。具体步骤如算法2 所示，算法流程如图1 所示。

图1 MRFKNCN 算法流程Fig.1 Procedure of MRFKNCN algorithm

算法2MRFKNCN 算法

输入近质心近邻个数k，待测样本点y，训练样本集T，模糊强度参数m

输出待测试样本y的类别

步骤1利用式（9）计算训练样本的密度。

步骤2利用式（10）和式（11）计算最小包围球的类中心和半径。

步骤3利用式（12）计算训练样本隶属度。

步骤4通过基于冗余分析的Relief-F 算法计算所有特征的权重。

步骤5利用式（15）计算待测样本与训练样本之间的加权欧氏距离，找出k个近质心近邻集合。

步骤6利用式（16）计算待测样本的模糊隶属度。

步骤7根据最大隶属度原则确定待分类样本的类别。

2.4 算法复杂度分析

假设n表示数据集的规模，p表示特征维数，k表示近邻个数，M表示类别个数。基于隶属度的模糊k 近质心近邻算法的时间复杂度主要来源于以下5 个部分：1）通过密度聚类思想计算训练样本的隶属度，时间复杂度为O(np)；2）计算每个特征的特征权重，时间复杂度为O(npμ)；3）计算训练样本的质心，时间复杂度为O(nk)；4）待测样本到各个类的加权距离，时间复杂度为O(np)；5）通过最大隶属度原则确定待测样本的类别，时间复杂度为O(M)。因此，MRFKNCN 算法总的时间复杂度为O(2np+nk)。

3 仿真实验与分析

3.1 数据集

为验证本文MRFKNCN 算法的有效性，选用UCI 和KEEL 中的11 个标准数据集和4 个含噪数据集进行仿真实验，所有实验都在Matlab2014b 的环境下完成。表2、表3 列出了实验中所用数据集的相关信息。

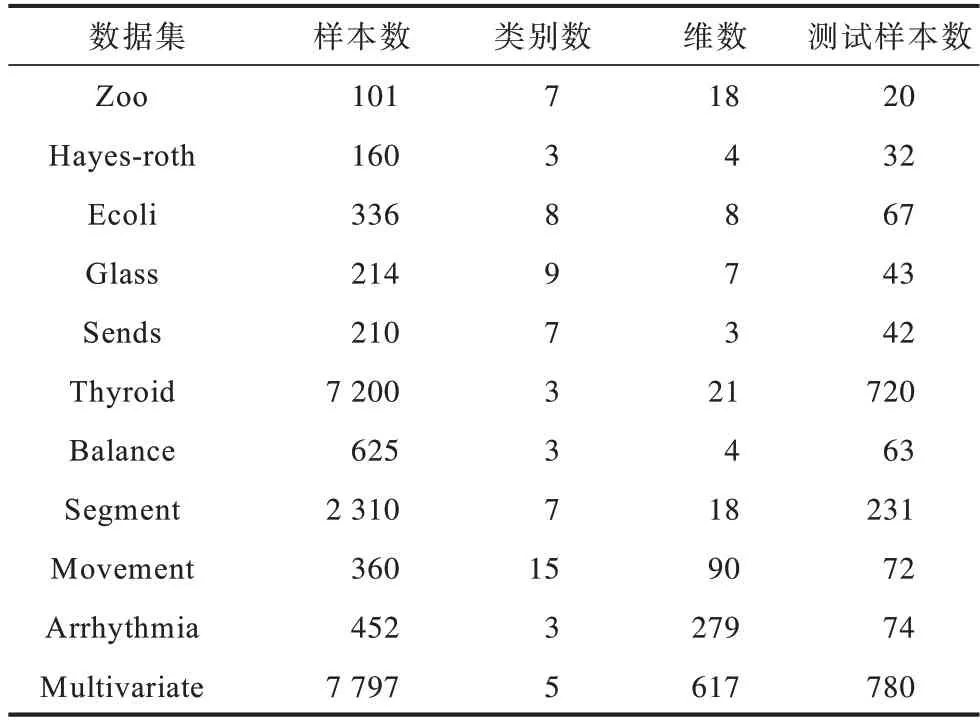
表2 标准数据集Table 2 Standard data sets

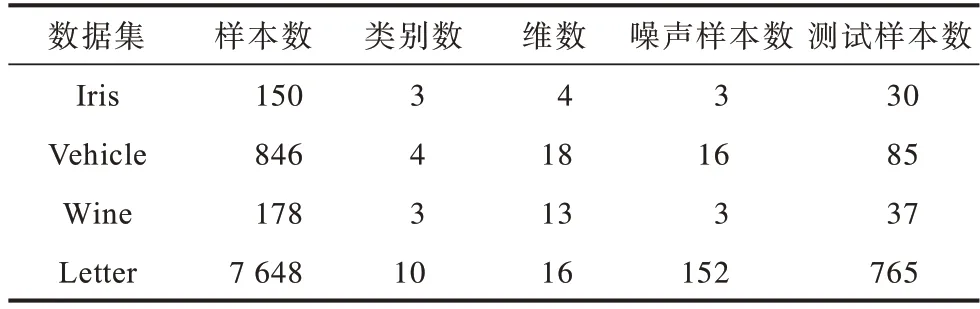
表3 含噪数据集Table 3 Datas sets with noise

3.2 算法参数设置

为了更好地测试各算法的分类效果，对本文算法所使用的相关参数进行调优。

参考文献［23］，取λ=2，δ=0.14 计算最小包围球的半径。计算完特征权重后，需要设置一个阈值Γ∊(0,1)［22］。对本文的数据集进行多次试验可知，当Γ=0.8 时，选出的新特征最具有代表性，模糊强度参数m=2，当模糊隶属度值与距离平方成反比时，在分类过程中会得到最优结果［18］。

3.3 实验结果与分析

本节设计了4 个实验来验证MRFKNCN 算法的有效性，将分类的准确率作为评价标准，比较本文算法与其他算法的性能。准确率的计算方法如下：

其中：Nc为正确分类的样本个数；Nt为实际分类的样本个数。

对于样本总数较小的数据集，通过10 次5 折交叉验证进行实验；对于样本总数大的数据集，通过10 次10 折交叉验证进行实验，最后将所有实验得到的准确率平均值作为测试结果。实验1～实验3 均采用交叉验证法确定最优k值。

3.3.1 MRFKNCN 算法总体性能分析

实验1为验证本文所提的新的隶属度函数在噪声点或离群点影响下的有效性，将MRFKNCN 算法与利用式（5）计算隶属度的FKNCN算法（命名为FKNCN1）及利用式（6）计算隶属度的FKNCN 算法（命名为FKNCN2）进行比较，运用表3 含噪数据集。实验结果如表4 所示。

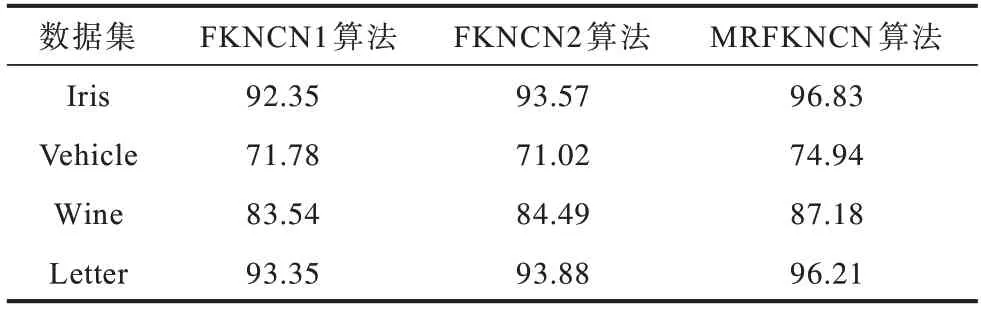
表4 MRFKNCN 与FKNCN 算法的平均准确率Table 4 Average accuracy of MRFKNCN and FKNCN algorithms %

表4 结果表明，当训练集中含有噪声点或离群点时，MRFKNCN 算法的平均准确率明显高于FKNCN1算法和FKNCN2 算法，在Iris、Vehicle、Wine、Letter 这4 个含噪数据集上，MRFKNCN 算法的平均准确率比FKNCN1 算法分别提高4.48、3.16、3.64、2.86个百分点，比FKNCN2算法分别提高3.26、3.92、2.69、2.33 个百分点，这表明本文所设计的新隶属度函数可以很好地识别出训练样本集中的噪声点或离群点，尤其是在Iris 小数据集中，MRFKNCN 算法获得了较高的准确率。

实验2为验证基于冗余分析的Relief-F 算法计算特征权重方法的有效性，将MRFKNCN 算法与未加权欧氏距离的MRFKNCN 算法（命名为MRFKNCN_N）、确定统一特征权重的MRFKNCN 算法（命名为MRFKNCN_U）进行对 比，运用 表3 中Arrhythmia、Segment、Zoo、Balance、Thyroid 这5 个数据集，3 种算法的平均准确率结果如图2 所示。

图2 3 种算法平均准确率对比Fig.2 Comparison of average accuracy of three algorithms

图2 结果表明，5 个数据集中MRFKNCN 的分类准确率都明显优于MRFKNCN_N 算法和MRFKNCN_U算法，说明不同的特征有不同的贡献率。因此，为了保证算法的准确率，应分别确定每个样本特征的权重，区分其差异，从而提高分类的性能。

实验3在最优k值下比较MRFKNCN、KNN［13］、KNCN［14］、LWKNCN［15］、FKNN［16］、FKNCN［18］和BMFKNCN［19］算法的分类平均准确率，所得结果如表5所示，其中加粗数字为最优值。

表5 最优k 值下MRFKNCN 与其他6 种算法的平均准确率Table 5 Average accuracy of MRFKNCN and other six algorithms under optimal k value %

表5 结果表明，虽然在Thyroid 数据集中，BMFKNCN算法取得了较高的准确率，但是MRFKNCN算法的准确率仍高于其他5 种对比算法。MRFKNCN算法在其余10 个数据集中的准确率都高于其他6 种对比算法的准确率，尤其是在Movement、Arrhythmia、Multivariate 这3 个高维数据集上的准确率大幅提升，说明MRFKNCN 算法不仅可以去除噪声样本对分类性能的影响，还可以选出有代表性的特征提高分类的准确率。同时，MRFKNCN 算法在11 个数据集中获得了最高的平均准确率。

3.3.2 MRFKNCN 算法在不同k值下的性能分析

实验4为了验证MRFKNCN 算法在不同k值下的分类性能，将MRFKNCN 算法与6 个对比算法在k=1～15时进行比较。运用表3的Hayes-roth、Ecoli、Glass、Sends、Cleveland 这5 个数据集。图3～图7 给出了7 种算法的分类准确率对比折线图。

图3 在Hayes-roth 数据集上的实验结果Fig.3 Experimental results on the Hayes-roth dataset

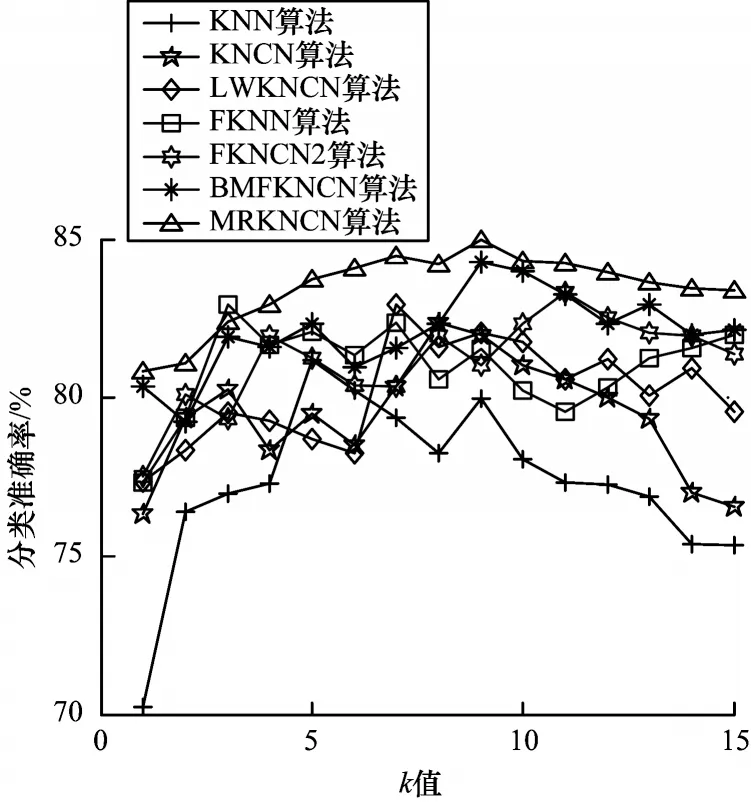
图4 在Ecoli 数据集上的实验结果Fig.4 Experimental results on the Ecoli dataset

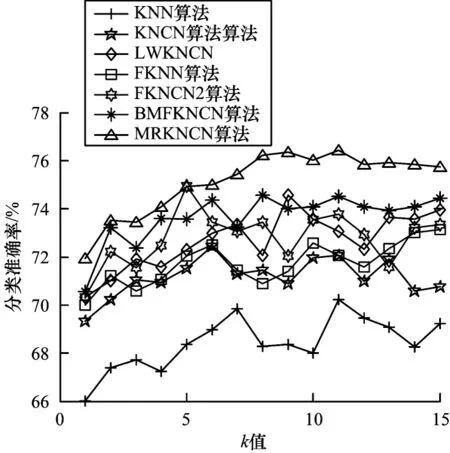
图5 在Glass 数据集上的实验结果Fig.5 Experimental results on the Glass dataset

图6 在Sends 数据集上的实验结果Fig.6 Experimental results on the Sends dataset

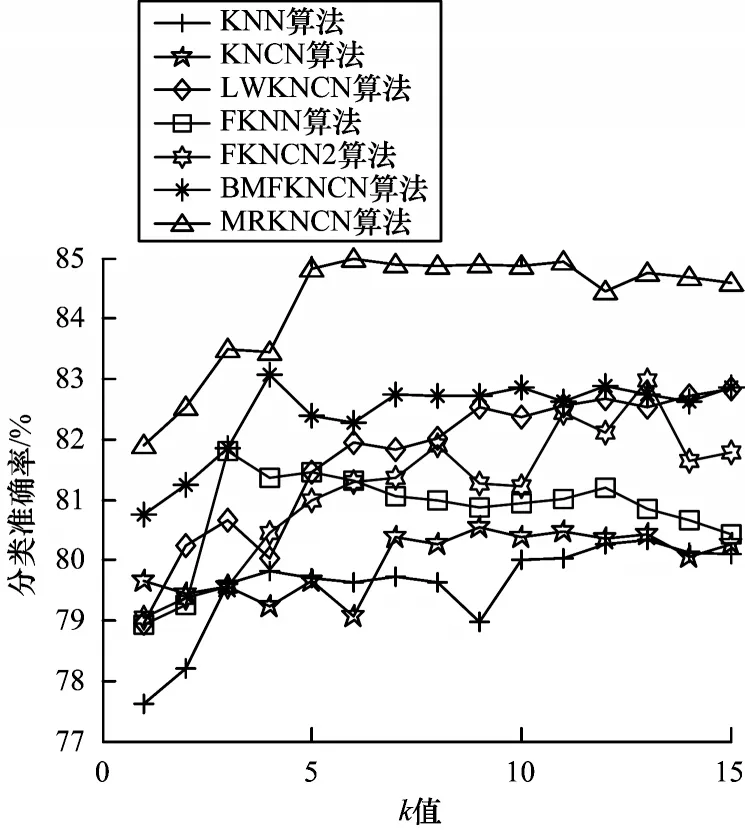
图7 在Movement 数据集上的实验结果Fig.7 Experimental results on the Movement dataset

4 结束语

针对FKNCN 算法未区别样本特征的不足，本文提出基于隶属度的模糊加权k 近质心近邻算法MRFKNCN。利用密度聚类思想设计新的隶属度函数计算训练样本的隶属度，通过基于冗余分析的Relief-F 算法计算每个特征的权重，删去不相关特征和冗余特征，选出重要的特征，并利用加权欧氏距离选取k个近质心近邻，最终根据最大隶属度原则对待测样本进行分类。该算法有效解决了训练样本中存在噪声样本或离群样本的问题，而且还为每个特征赋予不同的权重，更符合分类的实际情况。实验结果表明，MRFKNCN 算法在分类性能上明显优于其他对比算法。由于FKNCN 算法对参数k和模糊强度因子m敏感也会影响分类性能，因此下一步将研究如何自适应地优化FKNCN 算法的参数k和模糊强度因子m，进一步提高算法准确率。