地震诱发沙土液化对高速铁路车桥系统动力响应的影响分析

2022-07-14雷虎军陈奕涵朱广平

振动与冲击 2022年13期

雷虎军，陈奕涵，朱广平

(福建工程学院土木工程学院，福州 350118)

随着我国高速铁路网的不断延伸和加密，高速铁路桥梁位于液化场地的几率大大增加。液化场地由饱和无黏性土构成，动力荷载作用下，当其内部的超静孔隙水压力增大到与剪切面上的正应力相等时，土体会丧失抗剪强度，呈宏观上的“液体”状，简称“沙土液化”[1]。地震诱发砂土液化会导致地基承载力下降甚至失稳，如1964年美国的Alaska地震、日本的Niigata地震以及1976年中国的唐山地震等都出现了大面积砂土液化，并导致大量桥梁失稳破坏[2]。为避免沙土液化带来的地基失效问题，目前铁路桥梁抗震设计规范建议在液化场地采用群桩基础。群桩基础的使用可有效避免沙土液化时桥梁出现整体失稳，但沙土液化仍会降低土体对群桩的横向约束，进而改变桥梁的横向刚度。由于车桥系统对桥梁的横向刚度较为敏感[3]，地震诱发沙土液化可能进一步影响地震时桥上列车的行车安全性。由此可见，弄清沙土液化对地震时车桥系统动力响应的影响对于正确评价液化场地桥上列车的行车安全十分必要[4-7]。

车桥系统中沙土液化问题的实质是桥梁边界条件的改变，属桩土相互作用问题。已有部分学者针对车桥系统开展了桩土相互作用的相关研究。例如，李小珍等[8]使用BDAP V2.0程序对比分析了桥梁无桩模型和全桩模型的车桥耦合振动响应，在其研究中全桩模型采用弹性地基梁建立，桩土相互作用采用土弹簧实现并基于m法计算不同土层的弹簧刚度，该方法概念清晰、思路简单，但研究中忽略了土层阻尼的影响且无法模拟土的非线性特性；陈令坤等[9]利用ANSYS建立了简化的车桥耦合振动分析模型，并通过改进的Penzien模型模拟桩土相互作用，对比分析了不同工况下桩土相互作用的影响，该模型准确模拟了桩土非线性作用，但无法得到车辆、轮轨的动力响应；乔宏等[10]基于子结构法分别建立了车-桥子系统和桩基-地基子系统，通过迭代计算研究了桩土相互作用对车桥系统动力响应的影响，该方法可大大简化车桥系统中桩土相互作用的模拟，但模型参数计算复杂且无法模拟桩周土局部特性改变对耦合系统动力响应的影响；雷虎军等[11]采用Winkler地基梁模拟群桩基础，并利用m法计算弹簧参数，建立了地震作用下的车-轨-桥-群桩耦合振动模型，详细分析了桩土相互作用对耦合系统动力响应的影响，该模型中的桩土相互作用模拟方法与文献[8]一致，仍是基于线性的m法。地震诱发场地出现沙土液化后，桩土间的力学行为具有显著的非线性特征，要准确模拟需建立复杂的弹塑性力学模型，文献[12-14]进行了初步探索。由于铁路车桥系统具有时变非线性，模型规模大、计算耗时长，在其中进一步考虑沙土液化的影响，采用简化的桩土相互作用模型最为可行，目前针对该方面的研究还鲜有报道。

本文在以往研究的基础上，基于铁路大系统原理，采用Winkler地基梁模拟群桩基础并通过“m法”考虑桩土相互作用，建立了地震作用下的车-轨-桥-群桩耦合振动模型，并通过引入液化土力学指标折减系数Ψ考虑地基沙土液化。以某高速铁路(88+168+88)m预应力混凝土连续刚构桥为例，分别建立了土层未液化以及2种液化深度、3种不同液化程度的桥梁模型，通过输入典型地震波进行车桥耦合振动仿真计算，系统研究砂土液化对地震时车-轨-桥耦合系统动力响应的影响，研究成果可为液化场地高速铁路桥梁的行车安全评价提供参考。

1 地震-车-轨-桥-群桩耦合振动模型

地震作用下的车-轨-桥-群桩耦合振动模型是在原地震-车-轨-桥耦合振动模型的基础上增加群桩基础模型形成的，如图1所示。

图1 地震-车-轨-桥-群桩耦合振动模型Fig.1 Coupled vibration model of train-track-bridge-pile group under earthquake

其中，列车模型由一系列35个自由度的多刚体车辆模拟；轨道模型采用板式无砟轨道模拟；桥梁模型采用有限单元法建立，能够模拟任意桥型，上述模型的详细介绍可参考文献[15]。新增的群桩基础模型采用Winkler地基梁模拟，并通过土弹簧模拟土层对单桩的侧向约束，以此来简化考虑桩土相互作用。该方法最早由Reese提出[16]，并应用于我国的地基和基础设计规范，简称“m法”。在计算土弹簧的弹性刚度时，假设地基土各向同性、各方向抗力不耦合且地基系数随基础埋深线性增加。试验结果表明[17]，“m法”的计算精确度满足工程需求，土体的横向抗力σzx与单桩横向位移xz的关系如下

σzx=mzxz

(1)

式中：z为计算点的土层深度；m为地基系数的比例系数。由上式即可导出土弹簧的刚度Ks

(2)

式中：a为土层计算厚度；b0为基础侧面计算宽度。

地震诱发地基液化后，桩侧土对桩基的抗力会减小，液化程度越高、减小幅度越大。本文参照《抗规》附录C，采用液化土力学指标折减系数Ψ考虑桩周土的液化程度，如表1所示。

表1 液化土力学指标折减系数Tab.1 Mechanical index reduction factor of liquefied soil

对于液化土层，群桩基础模型中单桩的土弹簧刚度按下式修正

Ks=(1-ψ)·ab0mz

(3)

根据式(3)，即可在地震-车-轨-桥-群桩耦合振动模型中考虑地基沙土液化。根据上述理论，地震作用下的车-轨-桥-群桩耦合振动方程可统一表达为

(4)

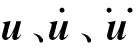
根据上述模型，利用既有列车-轨道-桥梁-地震分析程序TTBSAS[19]，即可实现地震作用下液化场地高速铁路桥梁-列车系统的耦合振动仿真计算，时域积分步长统一取为0.1 ms。

2 计算参数

以某高速铁路(88+168+88)m预应力混凝土连续刚构桥为例进行仿真计算，设计车速为250 km/h，结构总体布置如图2所示。其中，主梁为单箱单室变截面箱梁，顶板宽12 m、底板宽8 m，梁高6～12 m，腹板厚0.5～1.1 m，顶板厚0.62～1 m，底板厚0.52～1.1 m。桥墩采用空心墩，桩基为圆形钻孔灌注桩，1#墩和2#墩的桩径分别为2.5 m和2.8 m。梁体、桥墩分别采用C55和C40混凝土，承台和桩基采用C35混凝土。

图2 总体布置图(cm)Fig.2 General arrangement plan (cm)

根据该桥的地质条件，1#和2#桥墩承台底20 m范围内为可液化的砂质黏性土，群桩基础穿越可液化土层嵌固于基岩。在计算土弹簧的弹性刚度时，将地基土按2 m厚分层并依次编号，每层土的中点为土弹簧的刚度计算点。由于岩石的承载力强，其m值偏于保守地取块石类土的最大值，根据《地基》规范，1#和2#墩群桩基础的地质参数如表2所示。

表2 群桩基础地质参数Tab.2 Geological parameters of pile group foundation

《抗规》第4.0.2条规定：设防烈度为7度、8度或9度，地面以下15 m、20 m内，应通过试验判定地震时可液化土层是否液化。据此，本文考虑无液化以及两种液化深度：D=10 m和D=20 m，同时每种液化深度根据液化土力学指标折减系数考虑三种液化程度：Ψ=0.33、Ψ=0.66、Ψ=1.0，共7种群桩基础模型。采用MidasCivil 2020分别建立带有不同群桩基础的全桥有限元模型，并将其导入TTBSAS程序，即可得到本文耦合振动仿真计算的桥梁模型。

分别利用TTBSAS和Midas Civil 2020程序计算了不同桥梁模型的自振特性，部分振型特征对比如表3所示。结果表明：考虑地基沙土液化后，桥梁纵、横向自振周期均有所延长，且随着液化程度的增加桥梁的自振周期明显增大。由此可见，考虑地基沙土液化会增加结构的自振周期，且沙土液化对桥梁纵横向的影响大于竖向。

表3 模型自振频率及振型Tab.3 Natural frequency and mode shape of the model

此外，计算中的列车模型采用高速列车；轨道模型采用板式无砟轨道，轨道不平顺性采用德国低干扰轨道谱模拟，列车、轨道的详细参数参考文献[20]，分别如表4和表5所示。

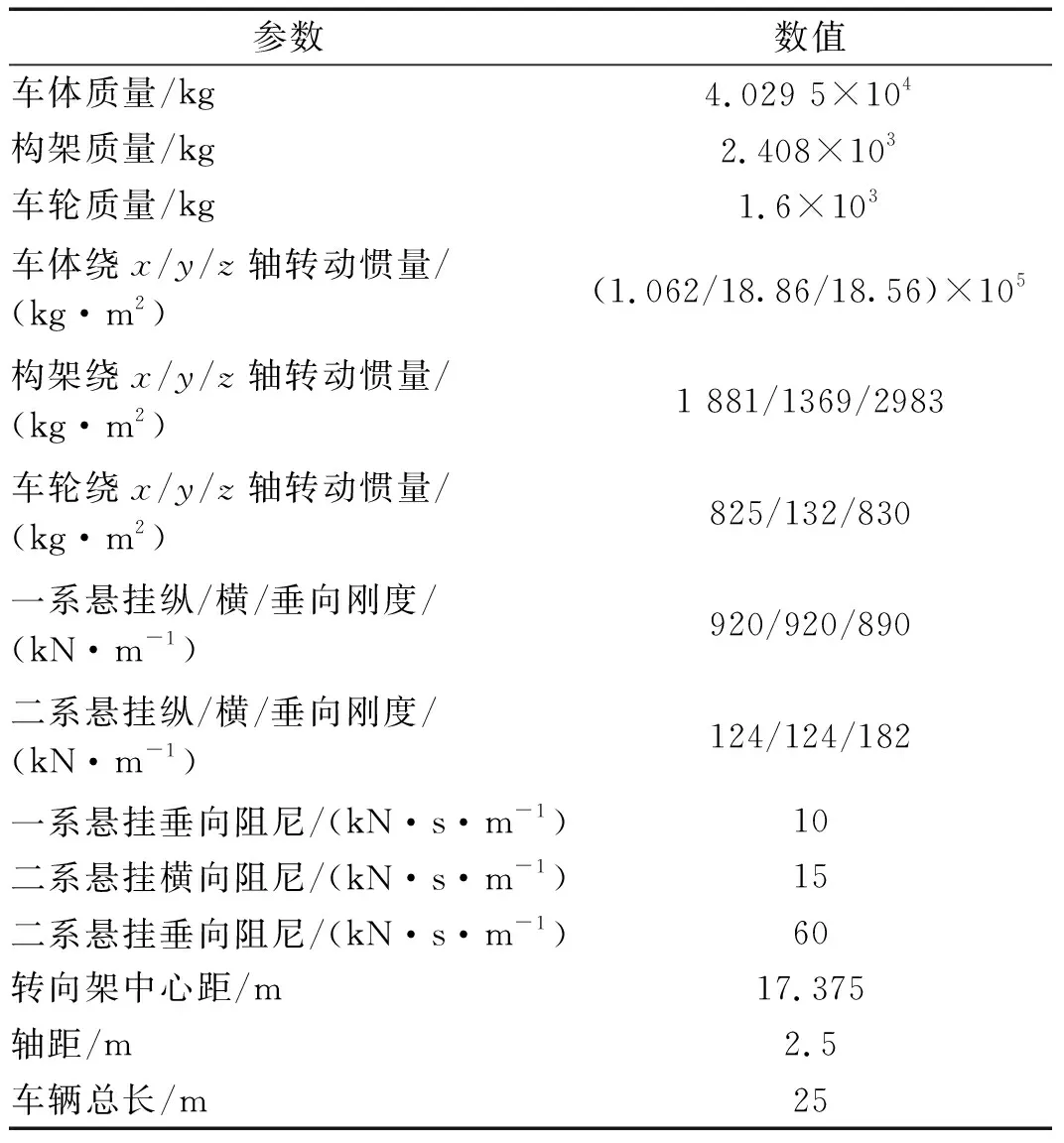
表4 车辆主要参数Tab.4 Main parameters of test train

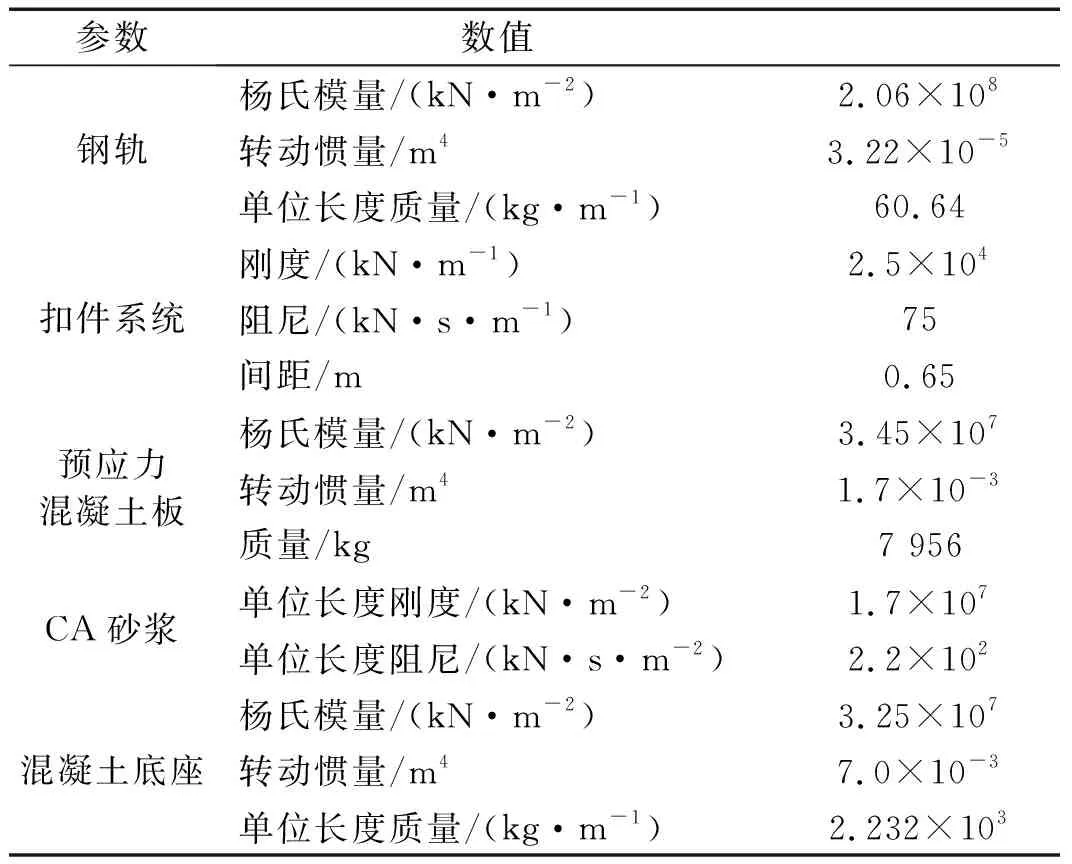
表5 板式无砟轨道主要参数Tab.5 Main parameters of non-ballasted slab track

该桥位于IV类场地，地震动反应谱特征周期Tg为0.75 s，设防烈度为7度，设计地震水平加速度峰值为0.1g。根据其加速度反应谱，人工生成了相应的地震波作为输入，其加速度时程及反应谱对比如图3所示。

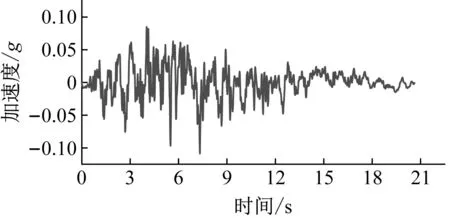
图3 输入地震波Fig.3 Input seismic wave

3 计算结果分析

3.1 液化深度的影响

首先考察液化深度对桥梁动力响应的影响。假设地震时液化土层完全液化，即液化土力学指标折减系数Ψ取1.0。当列车以设计车速250 km/h过桥时，无液化、液化深度10 m、液化深度20 m三种工况下桥梁跨中的横向位移时程和横向加速度时程对比如图4和图5所示。由图4和图5可得：当考虑场地沙土液化后，桥梁跨中的横向位移和横向加速度时程与不考虑液化时波形相似，尤其是液化深度为10 m时，其波形几乎完全一致，而在液化深度为20 m时，两者的波形变化趋势一致，但其峰值出现的时刻有差异。除此之外，考虑场地沙土液化后，桥梁跨中的横向位移和横向加速度时程峰值均比不考虑沙土液化时大。进一步对比不同液化深度下桥梁跨中的横向位移和横向加速度幅值，如图6所示。

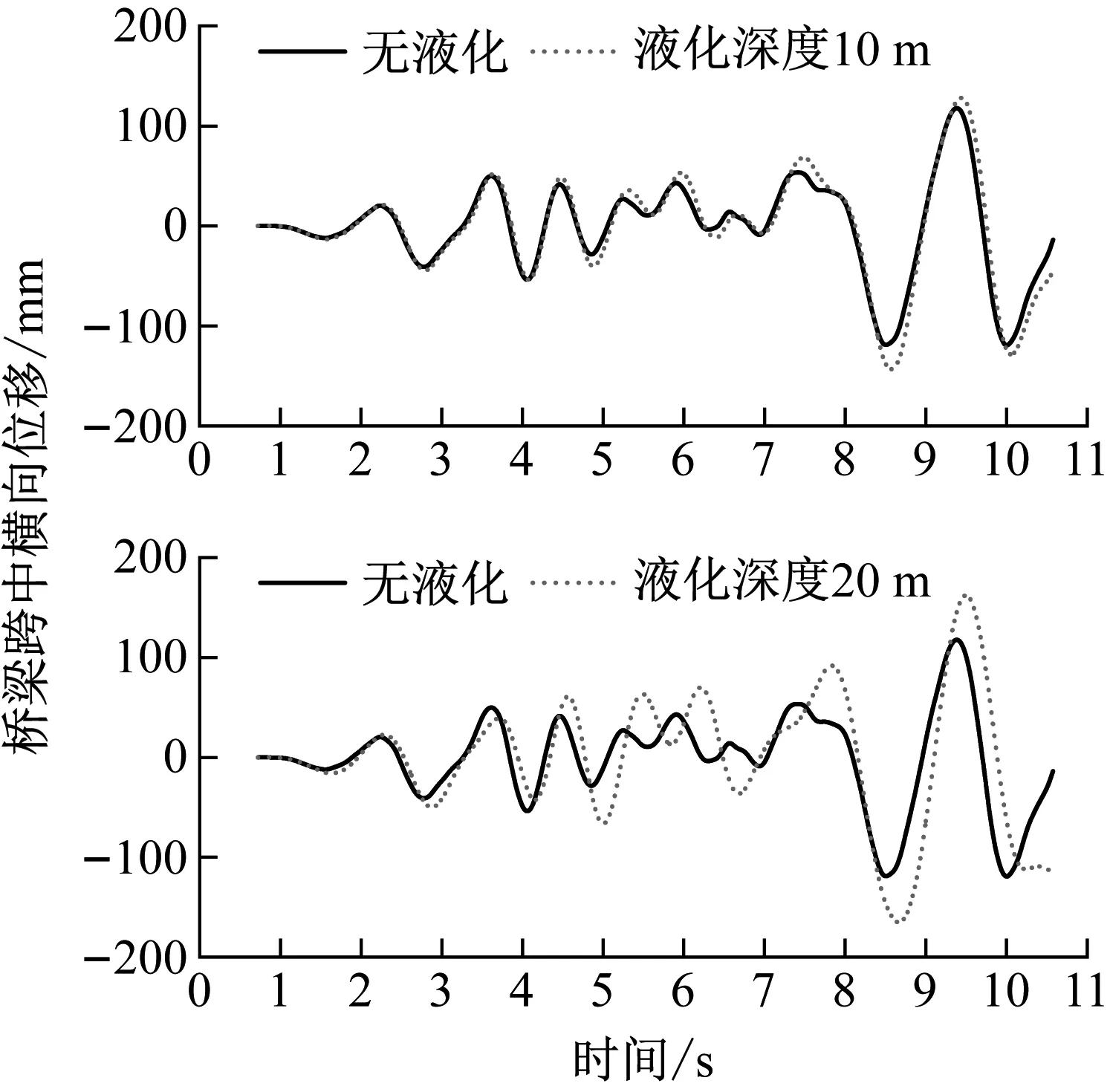
图4 不同液化深度下桥梁横向位移时程对比Fig.4 Time history comparison of lateral displacement of bridges under different liquefaction depths

图5 不同液化深度下桥梁横向加速度时程对比Fig.5 Time history comparison of lateral acceleration of bridges under different liquefaction depths

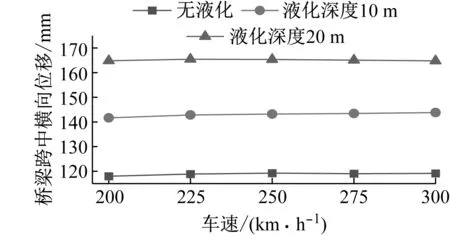
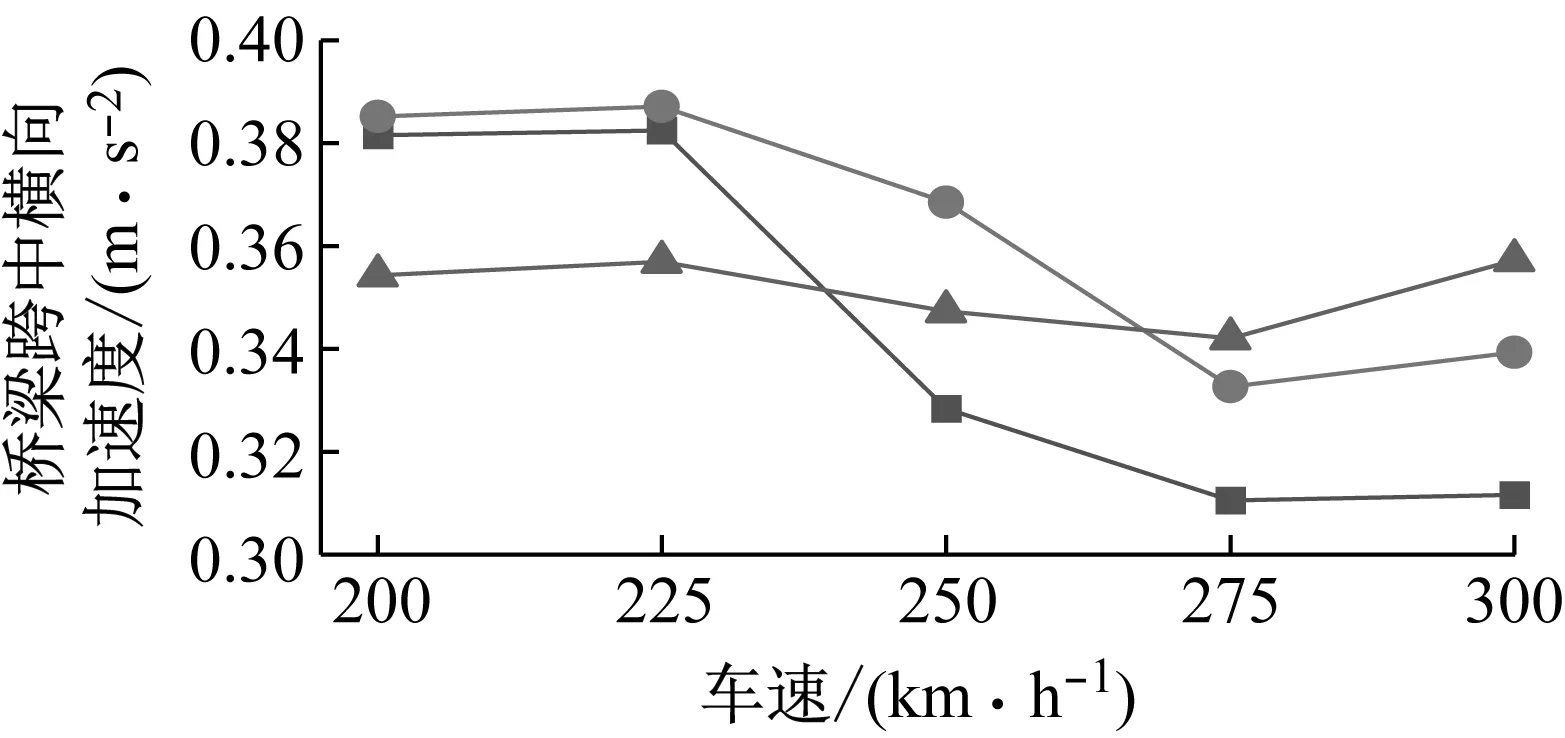
图6 不同液化深度下桥梁横向位移和加速度幅值对比Fig.6 Comparison of lateral displacement and acceleration amplitudes of bridges under different liquefaction depths

由图6可得：(1) 随着液化深度的增加，桥梁跨中的横向位移幅值均增大。其中，在车速为250 km/h时，液化深度10 m工况、液化深度20 m工况相对于无液化工况分别增大了20.1%和38.6%；(2) 随着液化深度的增加，桥梁跨中的横向加速度幅值变化规律较为复杂。其中，液化深度10 m工况的桥梁横向加速度幅值在不同车速下均比无液化工况大；而对于液化深度20 m工况，当车速为200 km/h和225 km/h时，桥梁跨中的横向加速度幅值小于无液化工况，且随着车速的增大，液化深度20 m工况的桥梁横向加速度幅值逐渐大于无液化工况和液化深度10 m工况。

分析原因可知，当地震诱发桥梁场地出现沙土液化时，液化的土层越厚，桩周土对桥梁群桩基础的横向约束越弱，桥梁的横向刚度降低越显著，其横向频率越低。根据反应谱理论，随着结构周期的延长，结构的位移响应会增加，加速度响应会降低。同时，对于高速铁路桥梁，它还受桥上列车的激振，且车速越快，横向激振力越大。由此可知，对于桥梁的位移响应，地震力起控制作用，桥梁跨中的横向位移会随液化深度的增加显著增大。而对于桥梁跨中的横向加速度响应，当液化深度为10 m时，列车的横向激振力起控制作用，当液化深度为20 m时，随着车速的增大其控制作用由地震力逐渐过渡到列车的横向激振力。因此，液化深度对高速铁路桥梁的位移和加速度响应均有较大影响。

进一步考察液化深度对桥上列车行车安全性的影响。本文根据TB 10002—2017《铁路桥涵设计规范》[21]，选取了5个指标进行参数分析以及用于后续的行车安全性评定。图7对比了不同液化深度下行车安全性指标1～5的幅值变化。

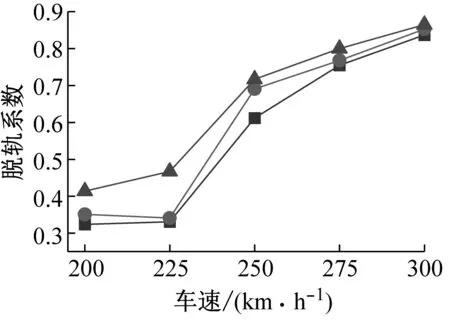
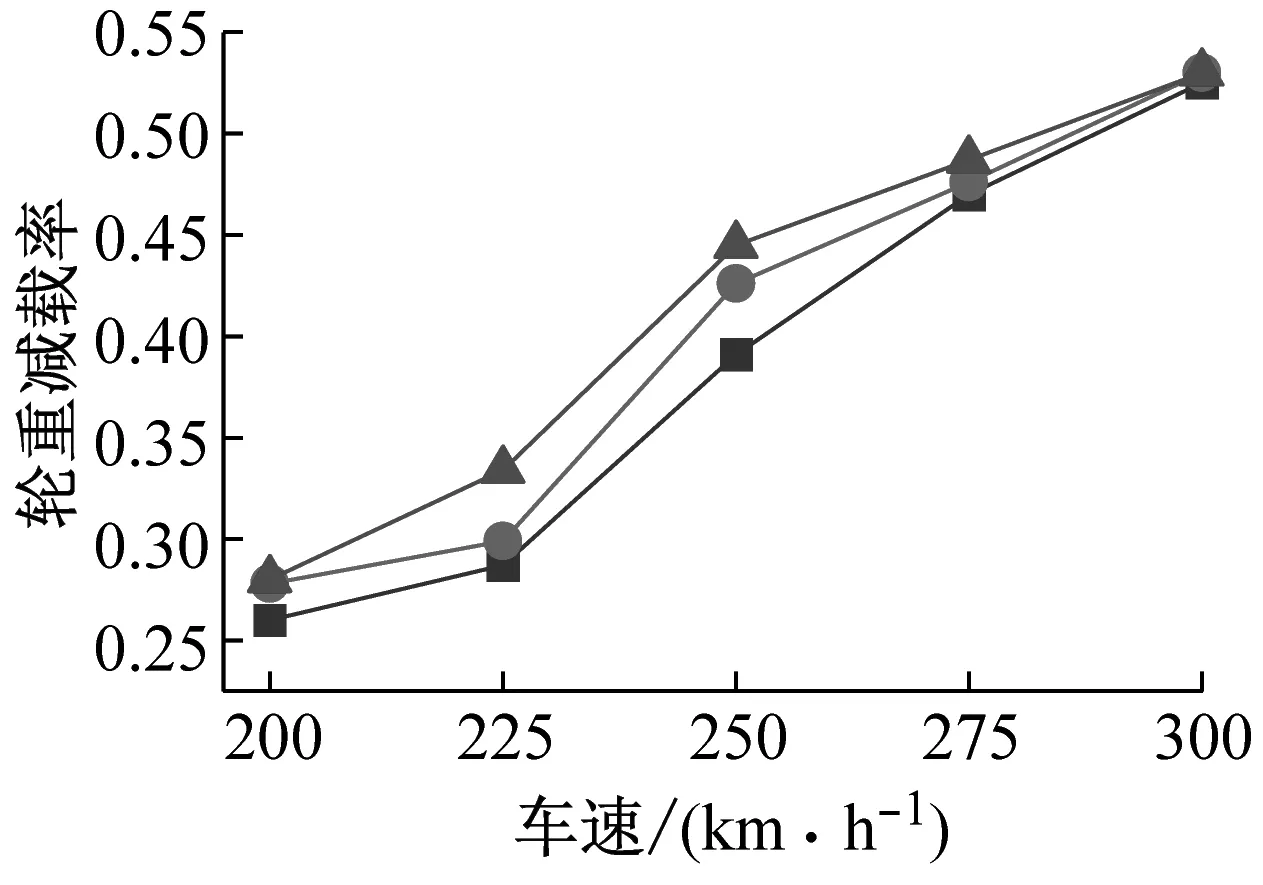
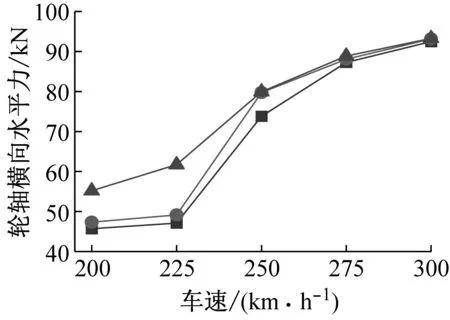
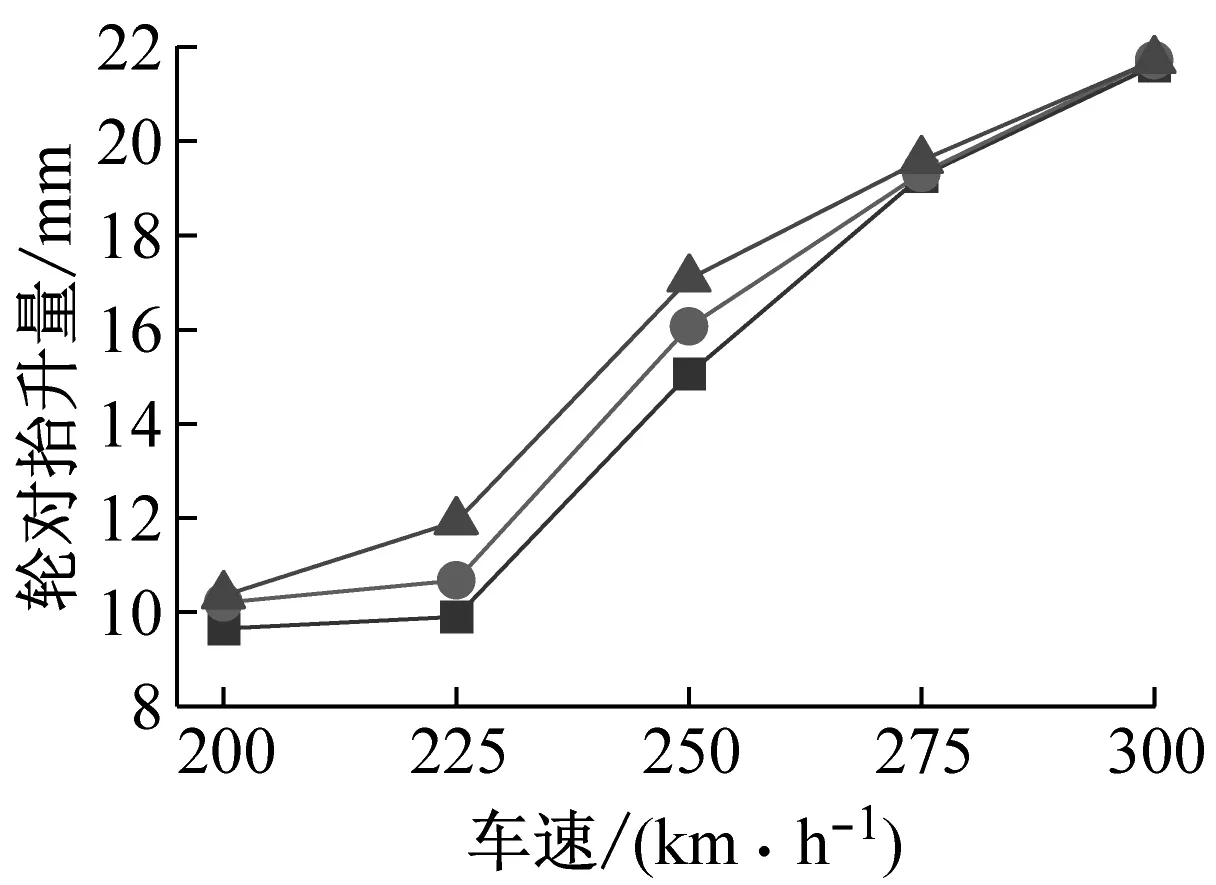
图7 不同液化深度下行车安全性指标对比Fig.7 Comparison of train safety indexes under different liquefaction depths

(5)

由图7可得：(1) 随着液化深度的增加，不同车速下的行车安全性指标均增大，但增幅小于桥梁跨中横向位移。其中，当车速为250 km/h时，液化深度20 m工况相对于无液化工况行车安全性指标1～5的增幅分别为17.2%、13.8%、8.3%、1.8%和13.4%。地震力通过桥梁作用于桥上轨道和列车，考虑沙土液化后，桥梁主梁横向位移会显著增大，从而引起桥上轨道的横向不平顺增加，进而影响桥上列车的行车安全性。同时，桥梁系统对地震波存在滤波作用，只允许与桥梁频率接近的地震波成分通过。因此，地震作用对桥梁的影响大于桥上列车；

(2) 随着车速的增大，液化深度对桥上列车行车安全性的影响逐渐减弱。例如：当车速为300 km/h时，液化深度20 m工况相对于无液化工况行车安全性指标1～5的增幅仅为0.9%、1.4%、0.9%、0.1%和0.5%，远小于车速为250 km/h时。这是由于当车速较低时，地震力起控制作用，此时液化深度对桥上列车行车安全性的影响较大，而随着车速的增加，列车的横向激振力逐渐增大，此时液化深度对桥上列车行车安全性的影响逐渐变小。

3.2 液化程度的影响

首先考察液化程度对桥梁动力响应的影响。假设液化层厚20 m，液化程度根据液化土力学指标折减系数Ψ分别取0、0.33、0.66和1，Ψ值取0表示无液化，Ψ值取1表示完全液化。地震作用下列车以设计车速250 km/h过桥时，不同液化程度下桥梁跨中的横向位移和横向加速度时程对比如图8和图9所示，其幅值随车速的变化如图10所示。

图8 不同液化程度下桥梁横向位移时程对比Fig.8 Time history comparison of lateral displacement of bridges under different liquefaction degrees

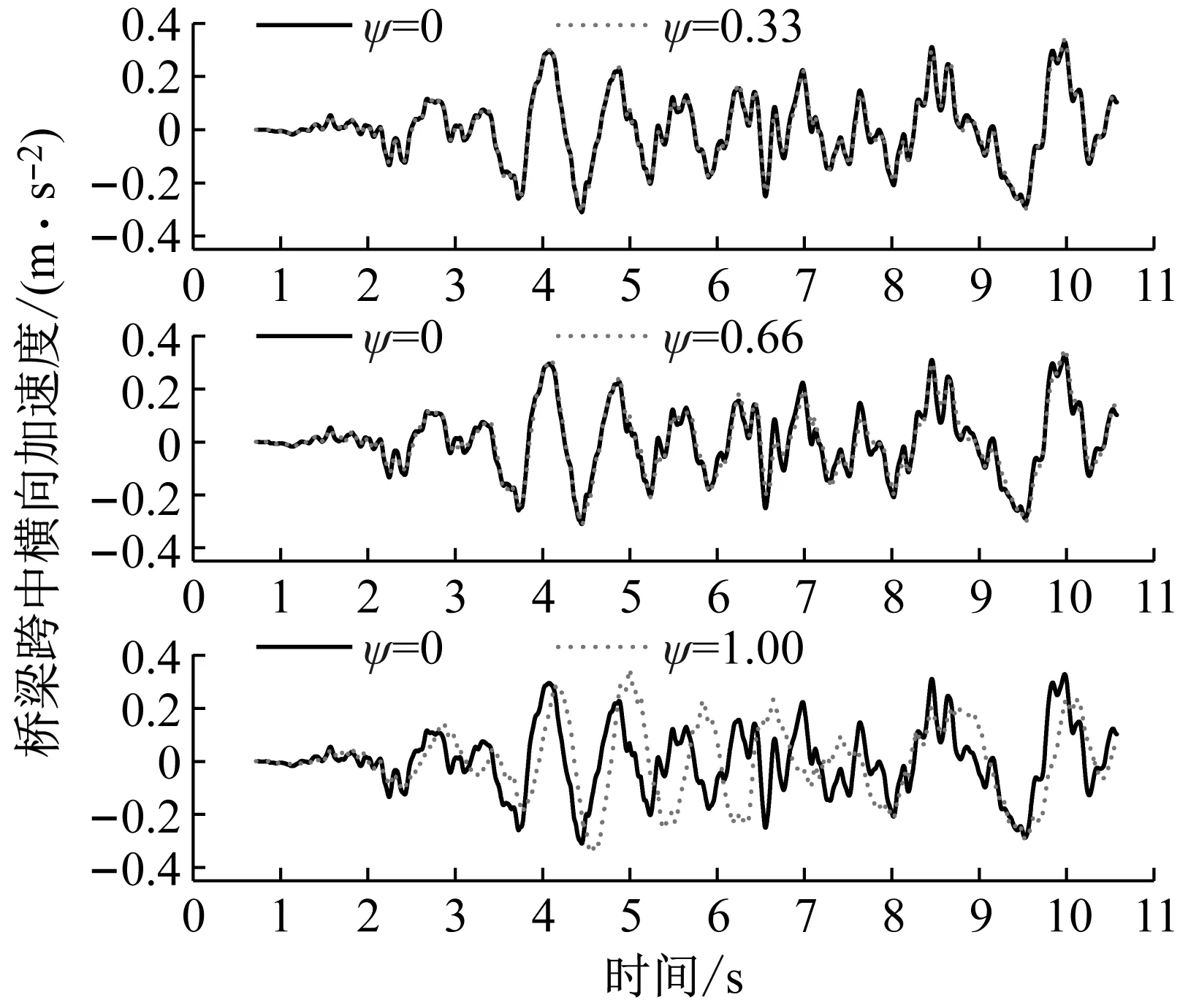
图9 不同液化程度下桥梁横向加速度时程对比Fig.9 Time history comparison of lateral acceleration of bridges under different liquefaction degrees

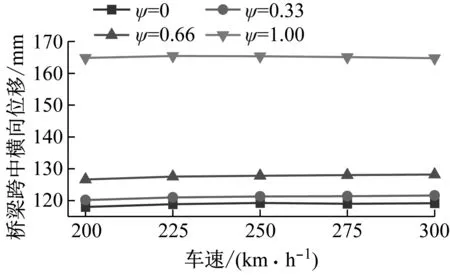
图10 不同液化程度下桥梁横向位移和加速度幅值对比Fig.10 Comparison of lateral displacement and acceleration amplitudes of bridges under different liquefaction degrees

由图8和图9可得：当液化层厚度保持不变，随着液化程度的增加，桥梁跨中的横向位移和横向加速度时程波形相似，尤其当液化土力学指标折减系数Ψ为0.33和0.66时，与无液化(Ψ为0.00)相比几乎完全一致；而当液化土力学指标折减系数Ψ为1.00时，桥梁跨中的横向位移和横向加速度时程波形有变化，且峰值时刻也不同。同时，随着液化程度的增加，桥梁跨中的横向位移和横向加速度峰值有增大的趋势。

由图10可得：(1) 随着液化程度的增加，桥梁跨中的横向位移幅值均增大，但增大速度并不均匀。其中，当车速为250 km/h时，液化土力学指标折减系数Ψ分别为0.33、0.66和1.00工况相对于Ψ为0工况下的桥梁跨中横向位移增幅分别为1.7%、7.2%和38.7%，增幅逐渐增大。

(2) 不同液化程度下，当列车以不同车速过桥时，桥梁跨中的横向加速度幅值变化规律较为复杂。其中，当液化土力学指标折减系数Ψ为0.33和0.66时，桥梁跨中的横向加速度幅值均比无液化时大，且液化程度越高、加速度幅值越大；而当液化土力学指标折减系数Ψ为1.00，车速由200 km/h增大至300 km/h时，桥梁跨中的横向加速度幅值先小于无液化工况，后逐渐增大。

(3) 通过与前述图6对比可以发现，不同液化程度下桥梁跨中的横向加速度幅值随车速的变化规律与不同液化深度下桥梁跨中的横向加速度幅值变化规律相似。

液化土力学指标折减系数Ψ越大，表明沙土液化程度越高，桩周土对桥梁群桩基础的约束作用越弱，结构的自振周期越长。因此，液化程度对桥梁动力响应的影响与液化深度类似，其本质是降低了结构的刚度、延长了结构周期，会显著增大桥梁的位移响应。此外，导致桥梁横向加速度幅值出现上述变化的原因也与液化深度的影响一致。

再进一步考察液化程度对桥上列车行车安全性的影响。不同液化程度下行车安全性指标1～5的幅值变化如图11所示。

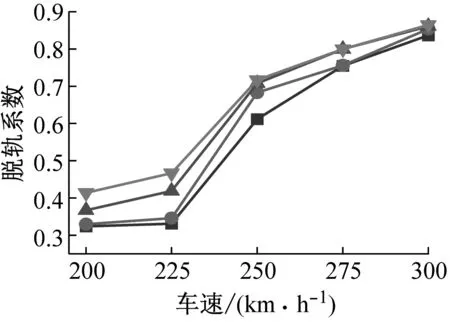
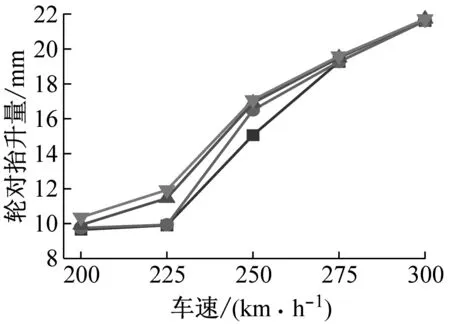
图11 不同液化程度下行车安全性指标对比Fig.11 Comparison of train safety indexes under different liquefaction degrees

由图11可得：(1) 随着液化程度的增加，不同车速下桥上列车的行车安全性指标1～5均有增大的趋势，同样其增幅也小于桥梁跨中的横向位移。其中，当列车以设计车速250 km/h过桥时，液化土力学指标折减系数Ψ为1.00工况相对于无液化工况的列车行车安全性指标1～5的增幅分别为17.2%、13.8%、8.3%、1.8%和13.4%。

(2) 随着车速的增大，液化程度对桥上列车行车安全性指标的影响逐渐减弱。当车速为300 km/h时，液化土力学指标折减系数Ψ为1.00工况相对于无液化工况下的列车行车安全性指标1～5的增幅分别仅为3.3%、1.0%、0.9%、0.1%和0.5%，远小于车速为250 km/h时。

(3) 通过对比图11和图7可以发现，液化程度对桥上列车行车安全性的影响与液化深度类似。不同液化程度和液化深度都会影响桥梁的横向刚度，进而影响桥上的轨道和列车系统，两者对桥上列车行车安全性指标的影响完全一致。

由此可见，液化程度也会显著影响桥上列车的行车安全性，且其影响机理与液化深度完全一致，在实际工程中可根据最不利原则进行仿真计算。

3.3 行车安全性探讨

进一步探讨无震、有震-不考虑沙土液化和有震-考虑沙土液化三种工况下列车过桥时的行车安全性，依次编号为工况1～工况3。根据前述分析，工况3中的液化深度取20 m、液化土力学指标折减系数Ψ取1.00，且对于CRH3高速列车，轮对横向水平力应≤62.3 kN。不同工况下行车安全性指标1～5的幅值对比如图12所示。

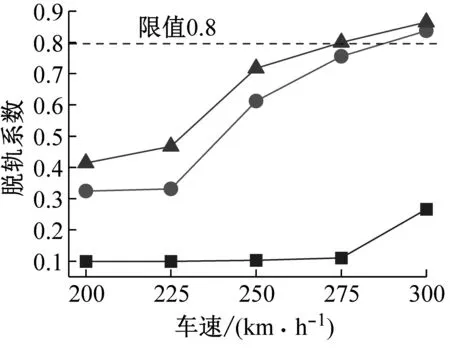
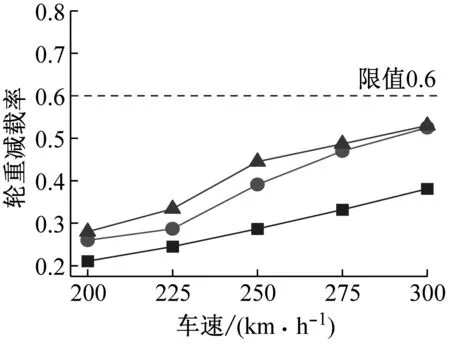
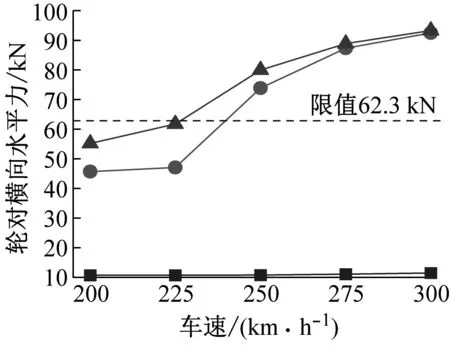
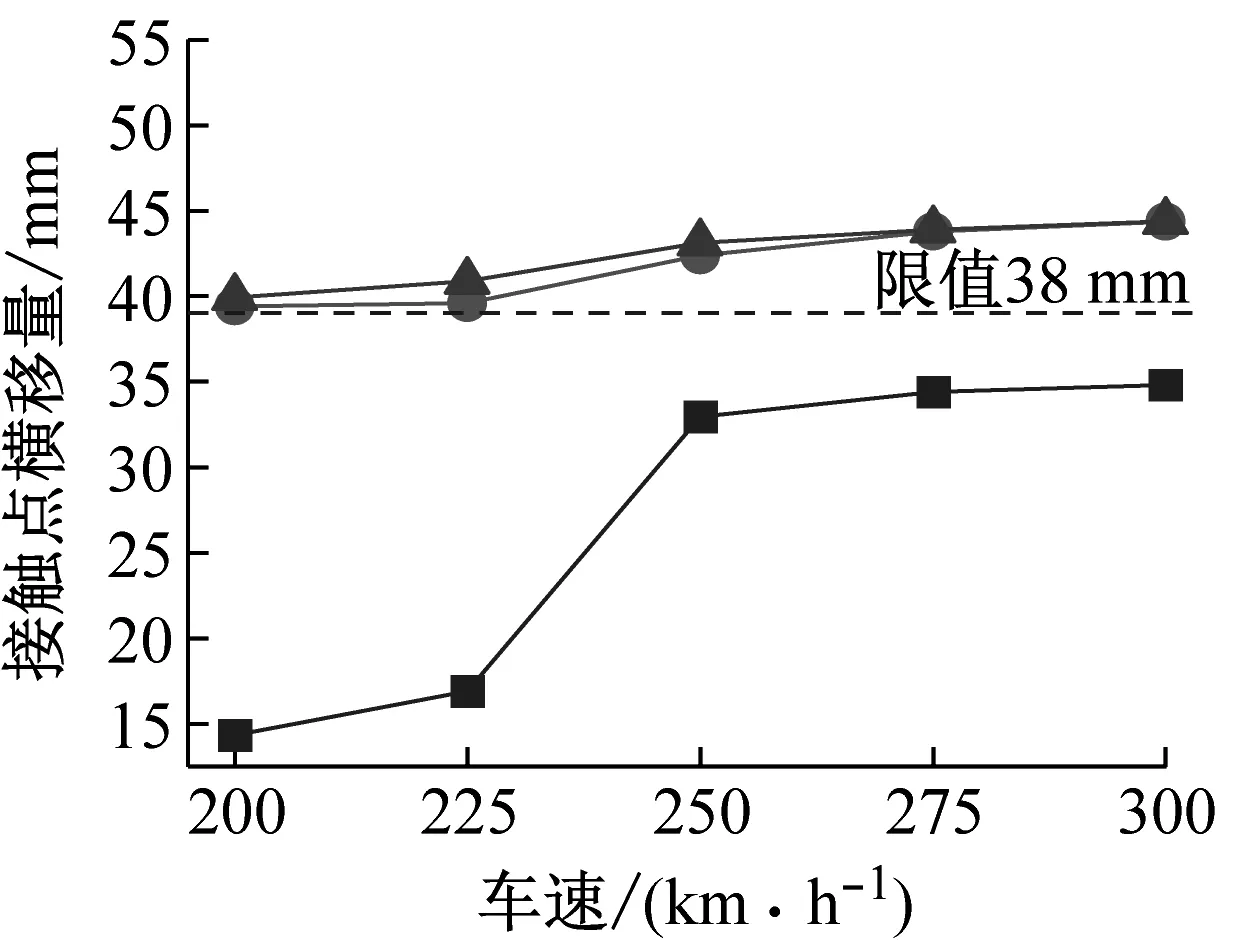
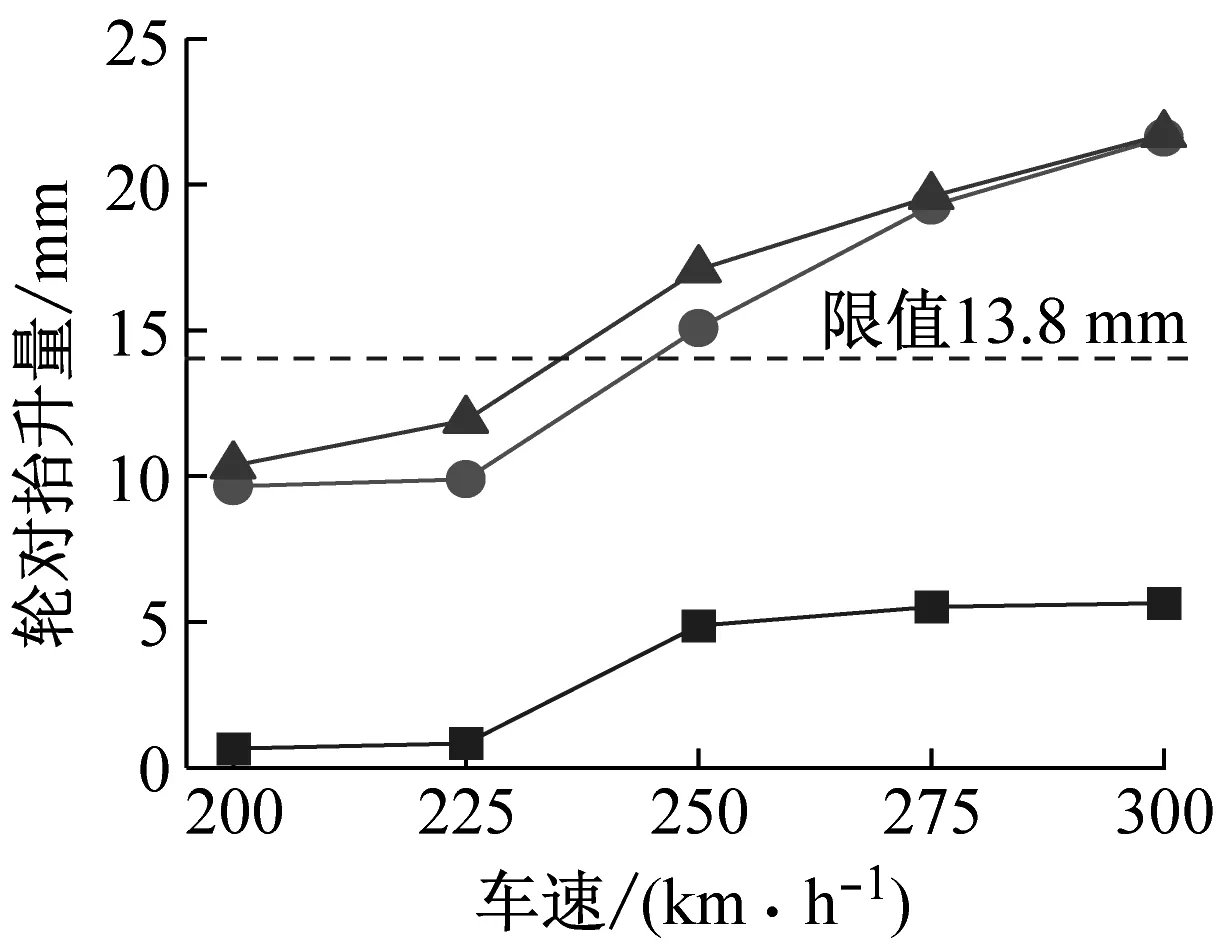
图12 不同工况下行车安全性指标对比Fig.12 Comparison of train safety indexes under different conditions

由图12可得：(1) 无震工况下，当计算车速由200 km/h按25 km/h间隔增大至300 km/h时，列车的行车安全性指标1～5均小于其限值。由此可见，对于本文的计算条件，无震工况下桥上列车的行车安全性满足要求。

(2) 有震工况下，列车的行车安全性指标随车速的增加而增大，且不同指标的超限车速不同。根据列车行车安全性指标1～5得到的安全车速阈值如表6所示。

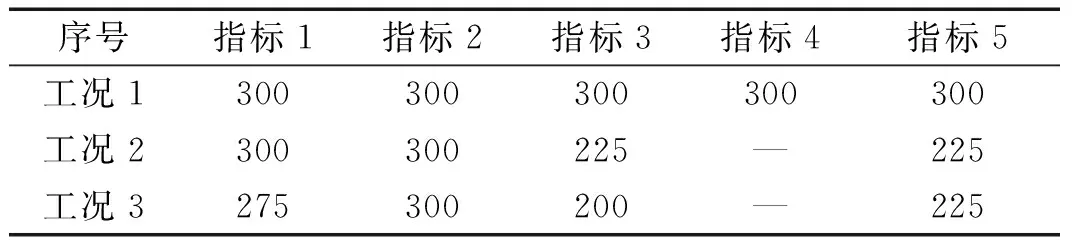
表6 列车的安全车速阈值Tab.6 Safety speed threshold of the train

由表4可得：对于列车的行车安全性指标1(脱轨系数)和指标3(轮对横向水平力)，不考虑沙土液化会高估列车过桥的安全车速阈值。其中，对于指标1，考虑与不考虑沙土液化时的安全车速阈值分别为275 km/h和300 km/h；对于指标3分别为200 km/h和225 km/h。而对于指标2、指标4和指标5，考虑与不考虑沙土液化时的安全车速阈值相同。由此可见，是否考虑场地沙土液化对地震时桥上列车的行车安全性评定有影响，建议在实际工程中考虑沙土液化的影响。