多传感器数据融合的复杂系统退化模式挖掘

2022-07-14彭宅铭程龙生姚启峰

振动与冲击 2022年13期

彭宅铭，程龙生，姚启峰

(1.江苏科技大学经济管理学院，江苏镇江 212100;2.南京理工大学经济管理学院，南京 210094)

随着复杂性、综合性和智能化水平的日益提升，现代装备系统逐渐发展成为具有更长寿命和更高可靠性的大规模复杂系统。由于系统结构复杂，各功能模块相互作用、相互依赖，关键部件的故障可能导致整个系统停止运行，给用户带来巨大的经济损失。复杂系统故障预测与健康管理(prognostics and health management， PHM)技术就是针对大型高价值复杂系统的自主保障、自主诊断的要求提出来的，该技术可利用先进的传感器获取系统运行状态信息，借助智能推理算法，实现系统状态的分析与监控、诊断与预测评估，对降低系统的维修成本、提高安全性与可靠性具有重要的意义[1]。退化模式挖掘是PHM技术的主要内容之一，该技术基于装备或系统的历史数据来构建状态评估模型，以此掌握不同环境下系统退化或降级的规律，挖掘可能存在的退化或降级模式，搭建全面的系统退化模式库。由于历史数据往往呈现时序性、高维性、复杂性、高噪声等特性，如果将其直接用于退化模式挖掘，不但在储存和计算上要花费高昂代价，而且可能会影响算法的准确性和可靠性。因此，有效的建立退化模式的方法就是对历史数据进行时间序列数据挖掘[2]。一方面，在降维或融合算法的基础上构建健康状态评估模型，以健康指数(health indicator，HI)曲线刻画系统的变化趋势；另一方面，利用时间序列聚类算法开展退化模式挖掘研究，探索不同的衰退模式。

复杂系统健康状态评估方法层出不穷，从HI构建的策略可以分为基于物理特征的健康指数(physics HI，PHI)方法和基于融合特征的健康指数(fusion HI，FHI)方法两类[3]。PHI方法主要使用统计方法或信号处理技术从监测信号中提取物理特征作为监测指标，如均方根、峰值、频谱特征和能量等。但这些PHI仅对特定性能退化阶段中特定故障敏感，无法满足系统全面健康状态监测的敏感性和稳定性。于是，在此基础上开发出了FHI方法，通过融合多个PHI或多传感器信号来构造表征系统健康状态和退化程度的参数。主成分分析法(PCA)能够在减少特征维数的同时保留尽可能多的信息，在FHI方法中也得到了大量的应用[4-6]。但是，PCA选择的主成分的物理特性往往难以解释。此外，特征融合方法，如神经网络[7]、遗传算法[8]、隐马尔可夫模型[9]、支持向量机[10]等方法也被广泛使用到FHI的构建中。这些算法的实用性在实践中都得到了验证，但无法描述特征对系统故障的敏感性和重要程度。马氏距离(Mahalanobis distance，MD)作为一种无量纲、尺度化的协方差距离，能够量化不同类别数据之间的差异，在构建FHI时表现出了较为理想的效果[11-12]。马田系统(Mahalanobis-Taguchi system，MTS)方法[13]是Taguchi提出的一种结合MD和质量工程学的多维模式识别方法，该算法可以在使用较小的样本量且没有任何先验信息的情况下，轻松地测量数据的异常程度并提供准确的结果。相比其它的特征融合算法，MTS不仅使用MD将所有相关信息融合为一个度量标准，而且能够识别出对故障信息敏感的特征。因此，MTS成为了当前部件或系统PHM的有效工具之一[14-15]。

时间序列聚类算法的主要过程是距离度量和聚类。在距离度量过程中，可选择多种不同的距离度量方法，如MD、欧式距离(Euclidean distance，ED)和动态时间弯曲(dynamic time warping，DTW)距离等[16]。相比MD和ED，DTW克服了点对点的缺陷，通过弯曲时间来测量长度不等的时间序列数据，能够实现数据点一对多匹配。因此，这种距离度量对时间偏差和幅度改变具有更强的稳健性[17]。在聚类算法选择上，层次聚类算法不仅不需要预先制定聚类数，而且能通过聚类结果准确描述整个聚类过程。因此，可利用DTW距离和层次聚类算法有效地挖掘滚动轴承的衰退模式[18]。

基于此，本文提出一种基于多传感器数据融合方法的复杂系统退化模式挖掘方法，通过改进MTS算法构建融合健康指数，利用分段点分析方法和基于DTW的层次聚类算法挖掘系统的不同退化模式，并利用航空发动机实例来验证所提方法的有效性。该方法充分利用现有系统全寿命周期数据，对系统衰退模式进行挖掘，为系统在线监测和剩余寿命预测提供依据，具有一定的理论价值和应用价值。

1 多传感器特征融合技术

复杂系统不同部件(或子系统)的传感器数据能够真实反映其性能状态，是其健康评估的基础。随着系统复杂程度的不断提升，数据维度也成倍增长，为在线评估和预测带来了挑战。根据PHM的内容，在对复杂系统进行健康状态评估前，需要通过数据采集、特征提取和特征选择等过程来提取有利故障特征，构建评估矩阵，基于评估矩阵构建健康状态评估模型，以此来量化评估系统的健康水平。

MTS将MD与质量工程学中的正交表(OA)和信噪比(SNR)相结合，实现多维特征的筛选和融合。同时，得到的MD是一种协方差距离，可以通过计算样本与样本集“重心”的最近距离来量化两个样本的差异。但是，在实际操作中MTS方法也存在明显不足：在基准空间优化时利用OA和SNR筛选的特征子集未必是最好的[19]。为此，本文提出改进MTS(improved MTS，IMTS)算法，并将其运用到多传感器数据的降维和融合中，以此来构建FHI。

1.1 基于IMTS的退化参数筛选与融合

基于IMTS的退化参数筛选与融合过程主要有四个阶段，具体如下：

阶段1基准空间(MS)构建

该阶段是IMTS的基础，需要从连续的时间序列数据中区分出“正常样本”和“异常样本”，确定“正常样本”和计算MD值。

(1) 按照性能参数的退化程度进行样本选择，早期的T0个监测数据作为“正常样本”，末期T1监测数据作为“异常样本”；

(2) 计算“正常样本”的MD值。设xi(i=1,2,…,n)为n个包含p个变量的样品，xi=(xi1,xi2,…,xip)，xij为第i个样本的第j个变量的观测值，则第i个样品的马氏距离平方(简称马氏距离)为

(1)

阶段2基准空间有效性验证

在基准空间优化之前要对上一阶段构建的基准空间的有效性进行验证。

阶段3基准空间优化

Taguchi认为并非所有的特征对分类都有贡献，有些变量可能会产生冗余信息、增加计算的成本和复杂度，因此，需要对原始变量进行筛选，挑选出其中的重要特征作为分类依据。

ReliefF算法是Kononenko[20]于1994年提出的基于特征权重的特征选择算法。通过搜索当前样本的各种近邻，综合计算特征权重，将权重小于阈值的特征移除，以选择最优特征子集。该算法计算简单，易于理解，在分类问题的特征选择中具有独特优势。为此，本文使用ReliefF算法代替OAs和SNR方法优化基准空间。但是，在实际运用中发现，利用ReliefF算法选择的特征之间可能存在高相关性，出现特征冗余，导致式(1)中的S不可逆，使得MD值无法计算。因此，如果能在进行ReliefF选择之前消除特征之间的相关性，将会有效地解决此类问题。基于以上的理论和实践，提出基于相关性聚类和ReliefF算法的两阶段特征选择算法来优化基准空间，具体步骤如下：

(4) 分别计算特征之间相关性系数的绝对值rij，得到相关系数矩阵r；

(5) 根据r进行特征聚类，将特征相关性大于阈值δ1的特征聚为一类，得到k类特征子集；

(6) 利用ReliefF算法计算所有特征的权重Wj并选择每一类中权重最大的特征构成特征子集FS1；

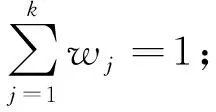
在上述过程中，步骤(5)和(6)利用相关系数聚类，可以消除特征集的高冗余性。本文选取Person相关系数，当其绝对值在0.8以上，认为特征间有强的相关性。因此，本文δ1选择在0.8～1.0之间。步骤(8)中的Sp类似于PCA中的累计贡献率，当Sp>δ2时可认为选择的特征子集可以解释原有的特征集，类似地，本文取δ2在0.85～1.0之间。

阶段4样本马氏距离计算

优化后的基准空间中包含初始特征集中的重要特征，可以利用其计算各样本的MD值。

(9) 利用优化后的基准空间计算样本的MD值：

(2)

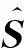
以上的IMTS方法操作简单，在降维时保持了特征集的分类能力，大大降低算法的复杂度。另外，利用该算法计算出的MD也是一种有效的刻画样本差异性的工具，可以作为表征系统性能状态的参数。

1.2 基于优化MD的健康指数构建

单一时刻的MD只能刻画系统偏离正常状态的程度，不能很好的反映该系统的健康状态变化过程，因此需要结合时间信息来获取相应的MD时间序列，以此来描述系统的退化过程及随时间偏移的程度。事实上，系统的健康状态遵循单调性原则，即如果没有进行人工干预(例如维修)，系统的健康状态不会随时间推移而改善，也不会突然出现大幅度下降(例如，从90%突然降到20%)。因此，需要根据单调性原则来计算HI，从而可以准确反映系统健康状况。

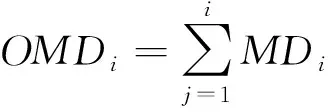
(3)

式中，OMDmin和OMDmax分别为系统全寿命周期样本计算的OMDi的最小值和最大值。

由式(3)可知，HIi∈[0,1]，且单调递减，值越大，系统越健康。系统整个寿命周期的HI曲线会呈现明显的变化趋势(如图1)。在整个过程中，曲线斜率均为负值，当系统处于稳定阶段时，曲线趋近于直线，而当系统逐渐退化，到达一定的阈值之后，曲线的斜率不断减小，直到HIi趋近于0。因此，通过以上方法定义的健康指数将有利于退化分段点确定。

图1 分段性能退化过程Fig.1 Piecewise performance degradation process

2 DTW层次聚类退化模式挖掘

2.1 退化分段点确定

假设某一系统全寿命周期共存在n个循环，其HI值记为H={h1,h2,…,hn}，对应的HI曲线图如图1所示。根据第1.2节的定义可知，HI存在图1中的退化分段点，该分段点的确定对于退化模式挖掘具有重要价值。

CUSUM(cumulative sum)算法是一种序贯分析技术，可以通过累积作用，将退化过程中的微小波动通过累计偏差反映出来，从而可以准确检测出退化分段点。CUSUM算法步骤如下：

(2) 令S0=0，计算累计和Sj：

(4)

(3) 寻找累积和Sj的极值点，即为退化分段点。

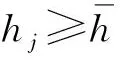
2.2 退化模式库构建

通过计算训练集样本的健康指数，建立健康指数曲线集合C={C1,C2,…,CN}。这些曲线记录了同一类型设备在不同环境中的运行状态，虽然各不相同，但存在具有类似退化趋势的样本。因此，有必要对健康指数曲线进行聚类分析，构建退化模式库。

DTW距离在计算时不要求两条时间序列具有相等的长度，可实现异步相似性比较，同时，对异常点不敏感。因此，DTW距离可以很好的作为健康指数曲线相似性度量的标准。层次聚类算法不需要预先设定聚类数，通过计算数据集样本间的相似性，不断的将相似性最高的样本合并构成新的集群，直到所有样本聚为一类。该算法的优势就在于可以表征聚类的全过程，同时可以清楚地知道各类之间的距离关系。为此，本文将利用DTW距离度量的层次聚类算法来挖掘系统的退化模式。具体步骤如下：

(1) 利用CUSUM算法确定N个健康指数曲线的分段点，并将退化阶段的健康指数曲线构成退化曲线集合D={D1,D2,…,DN}；

(2) 将单个退化曲线Di视为一类，计算Di和Dj之间的DTW距离dij，得到初始距离矩阵；

(3) 将初始距离矩阵中距离值及对应的退化曲线存放在数组DS={(Di,Dj,dij)|1≤i

(4) 将DS中dij最小的值对应的两条退化曲线合并为一类，形成新的聚类；

(5) 从DS中删除对应的类和距离值，计算新聚类与其它类之间的距离，更新距离矩阵；

(6) 重复步骤(3)～(5)，直到全部聚为一类；

(7) 根据设定的终止条件确定聚类数目k和聚类结果。

为更好地刻画新的聚类与其它类之间的特征，将新的聚类中所有样本到其它类之间距离的平均值作为类间距离。由于层次聚类的最终结果不是单一聚类，而是一个聚类层次，选择不同的终止条件将产生不同聚类数目。因此，选择一个合适的终止条件对聚类的结果有很大的影响。本文将根据类内相似度和退化时间区间确定不同类之间的阈值。

3.3 基于相似度的退化模式识别

基于相似度的退化模式识别的基本思想是找到与测试样本具有最高相似性的退化模式。对待测样本Y=[y1,y2,…,ym]T，yi=(yi1,yi2,…,yip)为第i个周期的特征数据，其退化模式识别步骤和流程如下：

(1) 利用IMTS优化的基准空间计算待测样本从开始运行到当前周期的MD值和MD累计和OMDi；

(2) 利用式(3)计算各时刻的健康指数HIi，得到HY=[HI1,HI2,…,HIm]T，其中OMDmin和OMDmax使用退化模式库中各模式样本的OMDmin最小值和OMDmax最大值；

(3) 根据退化模式库中的退化阈值确定Y的退化曲线DY；

(4) 计算DY与各退化模式Ci的相似度：

(5)

式中:Sim(Ci,j)为DY与Ci中每一条退化曲线D(j)的DTW距离;ni为模式Ci中退化曲线个数。

(5) 根据SIM(Ci)值和退化模式Ci的退化时间区间来确定Y所属的退化模式。模式Ci的退化时间区间定义为DTCi=[min(TCi),max(TCi)]，其中TCi为模式Ci中样本的退化时间，min(TCi)和max(TCi)分别为模式Ci中样本退化时间的最小值和最大值。假设测试样本Y所经历的退化时间为T，DY与模式Ci的相似度为SIM(Ci),i=1,2,…,l，将其按照从小到大排序为：SIM(Ck1)

①若T∈DTCk1，则Y属于模式Ck1；

②若T∉DTCk1，则Y不属于模式Ck1，进而判断T是否在DTCk2，若T∈DTCk2，则Y属于模式Ck2；以此类推，直到T在某一模式的退化时间区间内，则将其归为该类模式。

③若T不是任何一种模式的退化时间区间内，则将Y单独作为一类新的退化模式。

退化模式库的构建是一个不断学习的过程，在确定某样本的退化模式后，可将其加入相应的退化模式，更新模式库，以便更准确识别其他测试样本。退化模式识别的具体流程如图2所示。

图2 退化模式识别流程Fig.2 Flowchart of degradation pattern recognition

3 实验与分析

航空发动机是一个复杂的机电液磁耦合系统，其性能退化并不决定于某一个变量的退化，而是多个状态变量动态变化且相互耦合的结果，如温度、电压、振动等，所以必须充分利用多个传感器的特征参数，从中提取能体现系统退化特性的特征参数，才能准确了解航空发电机的退化状态。本文对美国国家航空航天局(NASA)提供的航空发动机全寿命周期退化仿真数据进行分析，该仿真数据是借助商用模块化航空推进器软件(C-MPASS)获得的。通过改变输入参数模拟风扇、高压涡轮、低压涡轮、高压压气机和低压压气机的故障和性能退化过程，利用传感器记录反映航空发动机运行状况的21个监测参数，其中包括低压压缩机出口温度(T24)、高压压缩机入口温度(T30)、高压压缩机出口压力(P30)、风扇物理转速(Nf)、核心机转速(NRc)、涵道比(BPR)、高压涡轮冷却引气流量(W31)、低压涡轮冷却引气流量(W32)和引气焓值(htBleed)等[21]。不同性能监测参数与航空发动机的退化状态有不同的相关性，根据训练集所有参数的散点图和局部加权回归(LOESS)散点平滑法选择有明显变化趋势的14 个参数构建航空发动机的状态矩阵。

本文选取FD001数据集，该数据集包含100个训练集样本，可作为历史数据进行退化模式挖掘。为验证方法的有效性和稳定性，利用5折交叉验证，随机选择其中的80个样本作为测试集，剩余20个样本作为测试集。以其中的一次交叉验证为例，介绍退化模式挖掘的流程，具体如下：

首先利用IMTS对历史样本数据进行分析，筛选对退化有利的特征。为消除发动机初期不稳定带来的影响，选取训练集中发动机的第6-10个周期飞行的数据作为正常样本，最终运行的5个周期飞行的数据作为异常样本，各包含500个样本。选择有变化趋势的参数构建航空发动机的评估矩阵。基准空间有效性验证结果显示，超过98.8%的正常样本的MD值小于异常样本的MD值的最小值，说明所建立的基准空间是有效的。利用特征之间的相关性，按照第1.1节进行特征聚类，取δ1=0.9。利用ReliefF算法计算特征的权重，并选择每一类中权重最大的特征构建特征子集，得到9个特征，将其按照标准化权重从大到小的顺序排列，如图3所示。

图3 特征的权重占比Fig.3 The weight ratio of each feature

由图可知，前6个特征的累积权重已经达到了93%，因此，选择NRc、T24、W31、P30、BPR、Nf构建优化基准空间。

分别计算训练集样本的全寿命周期的MD值和HI。利用CUSUM方法获取每个编号发动机的退化分段点和退化曲线。结果显示，航空发动机的退化阈值HIi0集中在0.6～0.9之间。结合航空发动机退化特性，取平均值HI0=0.745 0作为该类型发动机的退化阈值，即当健康指数大于0.745 0时，发动机缓慢退化，处于稳定阶段；当健康指数小于0.745 0时，发动机加速退化，处于退化阶段，直至完全失效。

根据退化阈值和健康指数曲线，确定发动机的退化曲线，如图4所示。

图4 发动机退化曲线图Fig.4 Degradation curve of engines

按照DTW层次聚类的步骤，得到如图5所示的聚类谱系图。聚类数目的选取对模式识别的准确率具有重要意义，本文基于以下三个原则来确定最佳聚类数目：①保证各类样本具有较高的类内相似性；②要求各退化模式得到的退化时间区间尽量不重叠；③各模式样本退化时间在剩余寿命预测允许的正向和负向预测误差(10和-13)内。经过多次试验，选择类内相似度阈值为85%，最终选择聚类数目为7，得到如表1所示的模式分类结果。分别选取各模式的样本和退化循环次数进行对比，如图6所示。

图5 DTW分层聚类谱系图Fig.5 Dendrogram of DTW hierarchical clustering

(a) 不同模式退化曲线对比

(b) 不同模式退化循环次数对比图6 不同退化模式对比Fig.6 Comparison of different degradation modes

表1 基于DTW聚类的模式聚类结果Tab.1 Model clustering results based on DTW clustering

由图6(a)可知，各模式的退化趋势有明显的差异。从表1中可以看出，不同退化模式经历的退化时间区间存在少量的重叠区域(模式四和模式五、模式五和模式六)，但从图6(b)中线箱图可以看出，不同模式的退化时间存在明显的差异。因此，可以利用得到的聚类结果和退化时间区间建立全面的系统退化模式库。

最后，利用建立的退化模式库和退化模式识别方法，对待测样本进行识别，识别结果如表2所示。

表2 模式识别结果Tab.2 Model recognition results

为度量模式识别的准确性，评估所有测试样本中正确识别的百分比，借鉴文献[21]中的准确率计算公式，构造如下的准确率计算公式

(6)

式中:N为待测样本个数;Cor(ei)表示识别结果，当识别的样本的退化时间在对应的模式区间内时，说明预测正确，此时Cor(ei)=1，反之Cor(ei)=0。

通过计算可知，除了一个样本被错误识别到模式七以外，剩余样本的识别准确率为100%。通过对比该样本退化曲线，该样本的退化时间不在任何一类中，因此，可将其归为单独一类。

为验证本文方法的稳定性，利用5折交叉验证，得到如表3所示的结果。结果显示，得到的模式数较为稳定，准确率较高，除了第1和第3次交叉验证出现的新模式被误识别外，其他测试样本均识别准确。因此，本文的退化模式聚类和识别方法是有效的，可以将其作为剩余寿命预测的依据。

表3 交叉验证结果Tab.3 Cross-validation results

为验证本文方法的在退化模式挖掘中的优势，选择文献[18]中的方法从健康指数构建和退化模式聚类两个层面进行对比。在健康指数构建方面，本文利用MD累计和构建的健康指数具有单调性，而且可以准确区分出稳定阶段和退化阶段，而文献中选择信号的时域特征作为退化趋势，不单调，且较难识别故障点。在退化模式聚类方面，航空发动机退化模式只与退化过程相关，本文利用退化曲线进行DTW聚类，而文献则使用整个寿命周期退化趋势进行DTW分段聚合，相比起来，本文方法更简便、合理。