某水电站进水口岩质边坡稳定性分析
2022-07-14徐向华
徐向华
(山东临沂水利工程总公司,山东 临沂 276000)
引 言
岩体边坡稳定性的探究是岩体工程中的一个热点研究方向,近年来我国的水利工程建设活动增多,出现了越来越多的大型水电工程建筑。建设活动也会受到场地条件的限制,有时候施工作业会因为地形环境的复杂而产生困难。为了应对客观环境造成的困难并保证工程施工的安全,需要进行各种边坡的挖掘,地形环境的限制会对水利水电工程的施工安全性、可行性与其所能产生的实际效益等产生影响[1~2],所以,进行岩质边坡稳定性的研究是非常有价值的。现今应用于边坡稳定性研究的方法比较多,本文的研究中岩体边坡安全性的设计应用的是极限平衡法,该方法的适用前提是基于滑体造成岩体破坏这一假设[3~4],进而得到能够符合设计稳定要求的相关数据参数,然后基于有限元模拟开展岩体边坡应力与变化关系的数值模拟研究,得出应力与变形参数,最后结合整体破坏得出岩体边坡的稳定系数。
1 岩体边坡稳定性分析
1.1 极限平衡法的基本原理
岩体在工程开挖时受到的影响主要是来自于施工爆破。由于受到卸荷松弛以及爆破损伤等影响,有较大的概率会造成岩体节理面延伸以及张裂的现象产生,尤其是在存在较多岩层分界面以及强节理面的岩质边坡中更容易产生[5]。岩体破碎很可能导致岩体滑落的状况产生,所以岩体边坡设计应该根据实际地形环境以及边坡形态。
第一步要进行力矩平衡参数的计算。F是强度储备系数,摩擦因数以及粘聚力分别为fi与ci。设分条竖向面上的法向力分别由Ei以及Ei+1来表示,Ti以及Ti+1为剪应力。另外,滑切面为Si,分条底部的法向力由Ni来表示。基于极限平衡以及屈服原则,列出如下滑裂面受力公式:
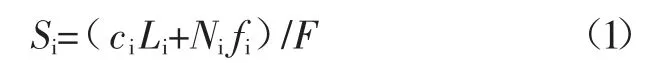
式(1)中,F是滑裂现象产生时的安全系数,而且F会受到力矩平衡条件的限制。在下述的推导中力矩平衡参数都是由Fm来表示。
从理论上来说,在力矩平衡条件的设定中,以任何位置当作中心平衡点都能符合要求。假设正方向为逆时针,原点O代表着中心点。在岩体边坡滑动状况产生时,以点对点的方式计算岩体的力矩,力矩的总和是零。据此可以得到滑裂面的安全系数在岩体边坡滑动状况产生时的具体公式表达:

式(2)成立的限制条件是整体力矩平衡。从理论上来说,如果水平力以及垂直力能够符合平衡的要求,那么力平衡的安全系数的具体公式依据其二中的任何一种平衡力都可以得到,但是,在实际的岩体边坡滑动现象中,除了一些特殊情况,滑动分量的力的分解一般来说其比重在垂直方向上是更小的。以水平方向的力为基础能够开展推导其整体的力学平衡条件,进而能够完成滑裂面安全系数数值大小的精准测算[6]。以上述条件为基础,能够得出岩体边坡投影大小在水平方向上为零时的安全系数的具体公式表达:

同时,垂直方向的力在岩体边坡的各方向作用力中是同等关键的,所以,垂直方向的力学平衡条件同理也必须得到满足,在岩体边坡投影大小在垂直方向上为零时,可以得到:

安全系数要以极限平衡法为基础开展研究,保证岩体状态稳定的力学假设条件能够依据极限平衡法得到满足。该力学假设条件的具体内容为:首先,岩体的材质的塑性以及刚性应该符合要求;另外,岩体边坡滑切面所承受的力的大小是恰好为临界值,而且此时的力学状态是与莫尔-库伦原则相符的[7]。
Ei、Ei+1、Ti以及Ti+1是一个位移边坡内力荷载群。对于Ni,Si以及强度储备系数F,设定F=Fm=Ff,同时这个条件的成立满足式(2)、(3)以及(4)。Ei、Ei+1、Ti以及Ti+1这组荷载群能够描述滑裂面的极限状态,F代表岩体边坡滑动时的安全系数。以上述描述为基础,然后利用极限平衡法将转换F,将其变成极值。
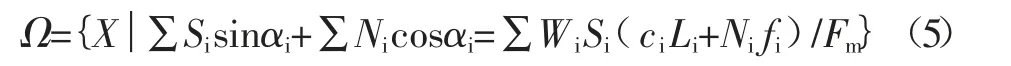
式(5)表示的是X的可行域范围Ω,上述的极值一定能够求解而且所得的解是唯一解。以相关力学原理为依据分析X,简化独立变量的同时会缩小X的可行域范围,进而能够求出边界稳定系数。
1.2 三维有限元计算基本原理
岩质边坡稳定性的分析与数值测算基于有限元模型计算分析结果更为精细,可以较好模拟岩体边坡变形过程,在这个过程中对于水利水电工程开挖和运作对岩体边坡变形规律以及应力分布所造成的影响状况要开展细致的探究,也包括岩体边坡所受到的渗流影响与支护的加固。采用有限元分析开展边坡的弹塑性研究,得到平衡方程:

在式(6)里,{F}e是等效节点力,{δ}e则是节点位移阵列。其中,刚度矩阵是[k],进而可以列出下式:

在式(7)里,[Dep]表示的是弹性矩阵。以塑性理论为依据,得到式(8):
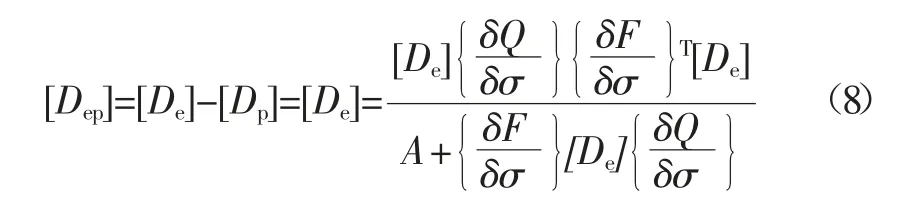
如果是理想化的材料,则其应该符合A=0。基于Drucker-Prager可以得到下式(9):

然后,基于莫尔-库伦准则开展上述两个参数I1以及J2的计算,可以得到:

基于莫尔-库伦准则,开展边坡岩体平衡方程的分析:

以弹塑性有限元为基础对加锚节理岩体进行数值的等效,设定加锚节理岩体是由岩块与锚件的相互连接组成,则其岩体的结构能够被描述为:

等效模拟的岩体弹粘塑性应变增量是:
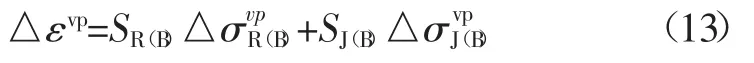
通常在实际的水利水电工程施工建设活动中与渗流相关的测算工作是比较繁杂的。在稳定渗流的问题分析中,裂缝岩体的处理应该按照等效连续的岩质属性来开展,然后得到如下有限元公式:

在上式中,Kx、Ky以及Kz分别指的是坐标系上对应的三个方向上的渗透函数,而q则指的是产水率。如果Kx=Ky=Kz,同时q=0,边坡岩体符合δH/δn=0。另外,在上式里,z指的是纵向坐标。以变分原理为基础,能够把上述问题变为一个极值问题[8]。基于Kx=Ky=Kz=K的假设条件同时忽略产水率,可得下式:

基于达西定律,稳定渗流水头函数应符合:
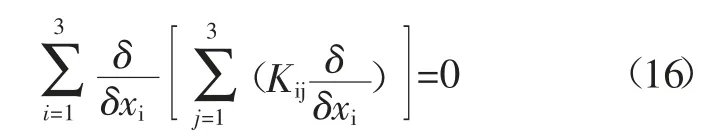
然后计算σ1、σ2以及σ3的稳定性:

2 计算结果分析
本文在岩体应力及其变化状态的测算中应用的计算方法是有限元模拟,通过这种方法在施工以及工程运作时去对边坡岩体的变化情况进行模拟,然后对比分析经由模拟得到的数据和实际监测活动中得到的数据。岩体边坡稳定性计算参数见表1。
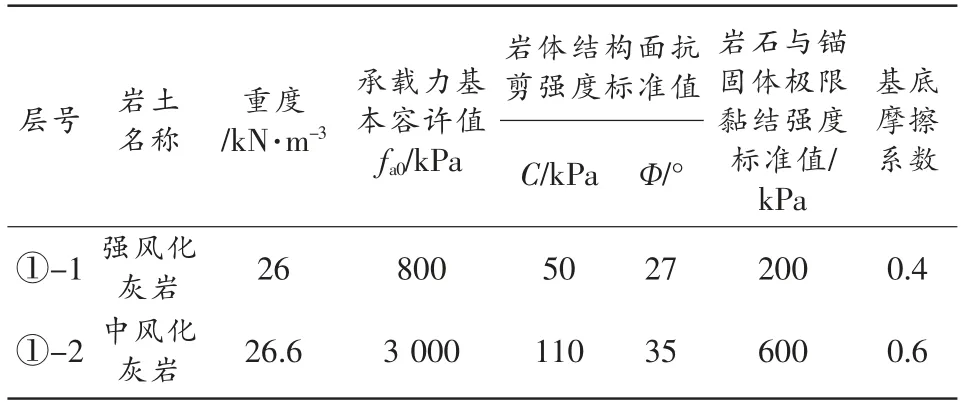
表1 边坡稳定性计算参数一览表
实验一:使用有限元法同时以进水口边坡岩体的实际地质状况以及岩组特点为依据去模拟分析岩体推进所受到的开挖活动对其造成的影响。对比通过有限元模拟得到的进水口岩体推进位移数据以及实际的开挖施工活动中监测得到的一号机器以及二号机器的安全系数数据。具体的数值情况分别如表2和表3所示,图1为通过有限元模拟得到的安全系数走势图。
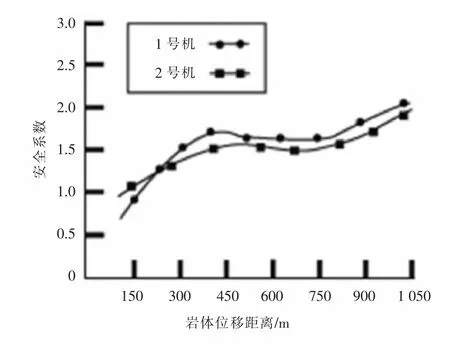
图1 边坡安全系数曲线图

表2 有限元法模拟计算结果
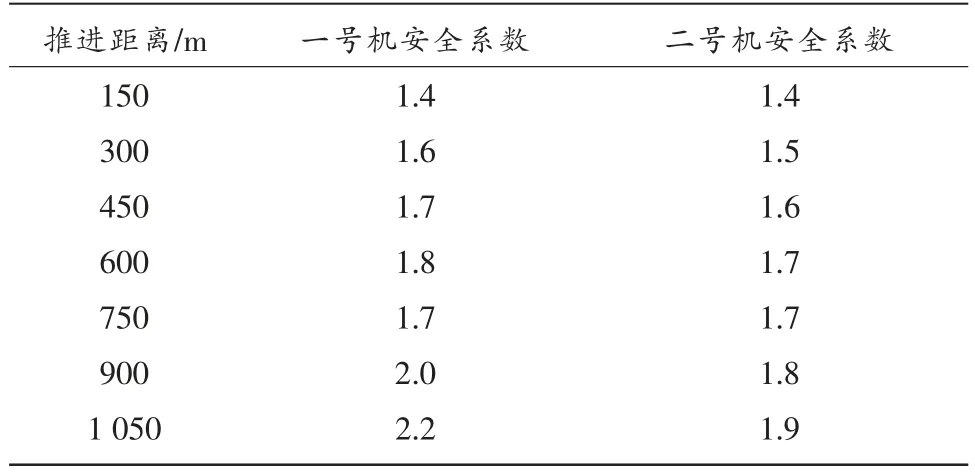
表3 实际边坡稳定监测数据计算结果
图2为天然工况下边坡稳定性位移云图,图3为天然工况下边坡最大主应力图。
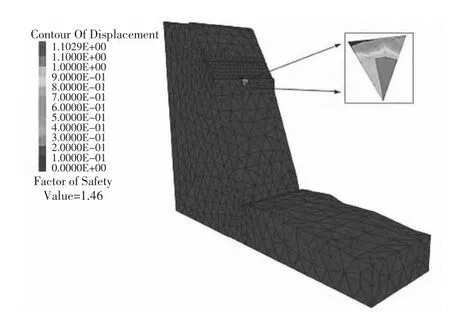
图2 天然工况下边坡稳定性位移云图

图3 天然工况下边坡最大主应力图
从表2中的数据能够看出,基于有限元模拟得到的二号机器的安全系数最小值是1.0,而且这个数据会跟着推进距离的增长而变大,后期其安全系数水平能够达到2.0,这也代表本文采用的研究方法是能够符合岩质边坡稳定性研究要求的。
实验二:水利水电工程正常运作时,其所处位置的自然环境气候状况能够影响其岩质边坡的稳定性。表4所示的是通过有限元模拟所得到的水利水电工程在不同工况下正常运行时的稳定系数数据情况,而表5中的数据是通过文献方法得到的。将上述两个表中的数据结果进行对比,能够为水利水电工程的相关研究提供参考资料。

表4 有限元法计算稳定系数

表5 极限平衡法计算稳定系数
通过对比,同时结合实际状况能够发现,相较于文献方法[9]得到的数据结果,通过有限元模拟得到的数据更加符合实际情况,通过文献法得到的数据结果普遍较小。
3 结 论
本文通过极限平衡法设计岩质边坡的稳定性,同时基于力学原理以及莫尔-库伦准则推导分析求得平衡状态下的安全系数,然后通过岩质边坡的数值模拟结果来分析其稳定状态。通过本文的探究分析能够发现通过有限元模拟得到的岩质稳定性数据是具有应用价值的,能够给水利水电工程相关应用研究活动提供参考。

