基于Guyan缩聚的模型修正方法在管道结构的应用

2022-07-14张明辉戴纳新

特种结构 2022年3期

张明辉戴纳新

南华大学土木工程学院衡阳 421000

引言

近些年，核能因其良好的安全性和经济型等优点被大量使用。但切尔诺贝利和福岛核事故对世界核电的发展造成了巨大的负面影响，暴露出了当前核工业不足之处。核电站管道的动力学分析一直是行业研究的热点问题，为了能够精确的掌握管道结构的动力学特性，必须对研究对象建立精确可靠的模型。错误或误差较大的动力学分析是没有价值的，甚至会造成巨大的工程事故。

当前，主要通过试验建模和理论建模两种方法了解结构的动力学特性。试验建模是基于试验模态分析方法，对结构进行试验测试，再利用采集到的测试数据通过模态参数识别技术识别出结构的模态参数，从而了解结构的动力学特性。研究人员认为试验测试能够反映出研究对象真实的动力学特性，实验建模的结果是可靠的。理论建模主要是利用有限元［1］方法，利用仿真技术在计算机中计算出建立的有限元模型，得到仿真模型的动力学特性。有限元建模可以在设计初期完成理论分析，为整个设计减小出错率以及缩短工期。但有限元方法中隐含了许多的假设和简化，例如实际工程管道系统焊接处、法兰与阀门等都会影响到有限元模型的建立。利用实测数据来修正有限元模型，使有限元模型的结果更贴合实际结果，解决有限元建模的缺陷。

有限元模型修正中最主要的两部分是自由度匹配和修正算法。由于测试点布置的局限性和部分自由度难以测量。测试振型自由度一般均小于有限元模型自由度数量，特别是复杂庞大的管道系统，有限元模型的自由度可能成千上万，然而试验测量数据一般仅有几十或几百。因此，需要对自由度进行匹配。

目前，主要有模型缩聚法和模态扩阶法。前者是将有限元模型缩减到与试验测量的自由度保持一致，后者是把测量振型扩展到与有限元模型具有相同的自由度数。模型缩聚后求出的特征参数与实测的特征参数符合，并且能保证将其带回完成自由度下的有限元后，二者仍能保持一致。模态扩阶法在扩展过程中保留了原有的试验误差，并且试验自由度数量远小于有限元模型自由度数量，因此模态扩展可能会将试验误差进行放大处理。当前，常用的自由度匹配法是模型缩聚技术。模型缩聚不仅可以节省计算机资源，还能够提高工作效率。

现有的修正算法主要有迭代修正方法和直接修正方法两类［2］。迭代修正方法有明确的物理含义，但模型参数的选取十分严格，且需要进行大量的结构分析，限制其在复杂的结构中的广泛应用［3－5］。直接修正方法是一种基于独立变量、在准确约束条件下最小化函数的方法。这类方法不需要迭代计算，因此消除了计算发散和较大计算量的可能性。Baruch［6］和Berman［7］方法为直接修正方法中最常使用的解析方法。

1 直接模型修正方法

1.1 质量矩阵修正

Berman和Nagy［8］运用类似Baruch［6］修正刚度矩阵的方法，把试验测量结果作为参考基准，去修正分析质量矩阵和刚度矩阵。

质量矩阵的修正问题可看成运用已知的特征向量矩阵和质量矩阵的解析估计，推导出质量矩阵的最优解。通过约束最小化式：

并满足正交性约束条件：

利用拉格朗日乘子法，将约束方程代入该函数并进行最小化，计算得到：

其中，Γ是拉格朗日乘子矩阵，将式（3）与质量正交性联合，得出修正矩阵为：

1.2 刚度矩阵修正

根据上述修正后的质量矩阵，采用Baruch［6］方法对刚度矩阵进行修正。该方法是基于约束最小化技术，推导出满足对称性和特性方程约束的刚度矩阵最优解。

Baruch等利用范数进行最小化，即：

利用拉格朗日乘子算法将要最小化的增广函数表示为：

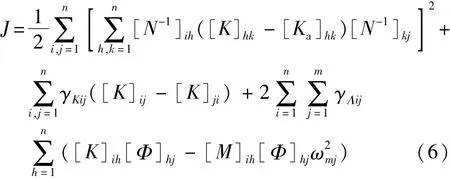
其中，ωmj为第j个测试得到的固有频率，拉格朗日乘子γΛij和γKij可表示为矩阵ΓΛ和ΓK的元素。

当拉格朗日乘子仅有下式约束时，产生唯一解：

对式（7）取待修正刚度矩阵（r，s）元素的偏微分，得到：

ΓK是反对称，经过整理可以得到K满足：

式子两侧都右乘Φ，利用特征向量矩阵的正交性和运动方程得到：

引入假设条件ΓTΛMaΦ是对称的，得到：

其中，将［I＋ΦΦTMa］矩阵取逆，才能得到式（11）的简化形式。

对于任意等幂矩阵A，都有：

在这种情况下，得到它的逆为：

把式子（13）代入到（11）中，得到ΓΛ满足等式：

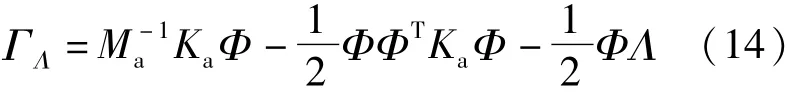
根据式（14）能够检查出ΓTΛMaΦ 是对称的，验证了前面的假设。将式（14）代入到式（9）中，合并同类项得到修正刚度矩阵的表达式为：

Baruch推导的刚度矩阵是唯一的，是式（5）优化的最小解。

2 模型修正的缩聚方法

2.1 Guyan缩聚法

Guyan［9］缩聚法完全忽略了副自由度的惯性影响得出了自由度转换矩阵，也成为静力缩聚法。Guyan缩聚法是一种非常经典的方法。该方法将结构自由度［X］分为主自由度［Xa］和副自由度［Xb］，根据主自由度和副自由度的相应位置，调整刚度矩阵和质量矩阵中元素的位置，在分块形式下的特征方程为：

展开公式（1）的第2 行可以得到：

忽略副自由度的惯性效应，得到副自由度与主自由度的关系：

从而得到结构自由度为：

其自由度转换矩阵T为：

此时式（4）可简化为：

将式（6）代入特征方程中，两端同时乘上TT，得到缩聚后的广义特征方程为：

MG和KG为缩聚后的质量矩阵和刚度矩阵，转换形式为：

2.2 IRS缩聚法

IRS［10］缩聚法是在静力缩聚的基础上，增加了惯性项使得缩聚后的精度有了进一步的提升。并且可以通过迭代运算进一步提高模型缩聚的精度。

将式（16）在频域内用分块矩阵表示为：

其中，ω是角频率。同式（17）整理得到：

将上述方程通过级数展开后，仅保留第一阶惯性项得到：若将所有惯性项去掉，即得到Guyan 缩聚法［9］。利用静力缩聚求出代入式（26）整理得到：

其中KS＝TT1KT1、MS＝TT1MT1，自由度转换矩阵T1为：

3 数值仿真

通过对两个算例进行模型修正，一是观察修正后结构结果的精确度，二是观察修正后结构在地震激励下的响应情况。本文利用有限元软件计算出真实的结构工况，将得到的结果作为试验数据代入到有限元模型修正中。通过Matlab［11］来进行大量的矩阵计算和动力分析。主要对修正后的有限元模型模态频率和时程分析的研究，目的在于为核管道在地震响应下更精确的模拟提供一种有效的方法。

3.1 实验室管道

本文模拟一个单端固定的实验室管道结构如图1 所示，管道长度为L＝2650mm，外径D＝60mm，厚度2.5mm，弹性模量E＝200GPa，泊松比0.3，密度7850kg／m3。“试验测试”数据来源于一个22 自由度模拟系统获得。由于管道处在热处理工艺下，导致管道材料属性发生了变化。假设实验管道材料的弹性模量发生了变化，将其弹性模量降低为原本的0.8 倍，其结果作为“试验测量”数据，对有限元模型进行修正。

图1 管道单元部分组成的模型示意Fig.1 Model schematic diagram of pipe unit parts

管道有限元模型采用的是单节点2 个自由度进行分析，分别是平动自由度和转动自由度。直管单元的结点位移为d＝（ui qj）T。除去约束，该管道共有20 个自由度。为了更好的修正管道模型，把仿真结果所获取的低阶频率和所有平动模态振型作为试验数据，代入到有限元模型中对质量矩阵和刚度矩阵进行修正。利用Guyan 缩聚方法来实现自由度匹配，通过编写Matlab程序将主副自由度进行分块处理，将管道中的平动向视为主自由度，转动向视为副自由度。有限元模型的刚度矩阵和质量矩阵缩聚后为一个10 ×10 的矩阵。运用刚度矩阵修正方法计算得到模型的特征值，如表1 所示给出了精确值（实际结构）、修正前和修正后的数值。

表1 管道前10 阶固有频率的对比Tab.1 Comparison of the first 10 natural frequencies of pipes

由于试验数据来源于仿真软件数据具有完备性，测量数据与有限元模型的自由度相匹配，不需要进行Guyan缩聚或模态扩阶，且修正后的计算结果与试验数据是一致的。在真实工况下，实测的自由度数量远低于有限元模型，相对于平动自由度来说，转动自由度难以测量。因此，仅考虑平动项的数据进行修正有限元模型。这样更符合真实的情况。通过表1可以看出，当有限元模型进行刚度矩阵修正后，计算出管道结构的固有频率能够较好的还原出真实的管道情况，相比修正前误差有很大的提升，相对误差均小于3.92182E-10 的绝对值。

本文同时也运用了IRS 模型缩聚技术实现自由度匹配如表2 所示，在模型缩聚中IRS 法相比Guyan缩聚法具有更好的效果，IRS 法中转换矩阵是将结构惯性量考虑进去。由于有限元刚度矩阵与真实的刚度矩阵存在误差，转换矩阵中多次引入含有误差的刚度矩阵，致使IRS 法在刚度矩阵修正后相比Guyan缩聚具有更大的误差。无论使用的是何种缩聚技术，经过刚度矩阵修正后其误差都比最初的有限元模拟提升了很多。说明在模型修正中，关键的影响因素是修正数据，在一定量的试验数据基础上误差与模型缩聚技术关联性不大。

表2 对比不同模型缩聚法下的固有频率Tab.2 Natural frequencies under modelreduction of different models

3.2 核电厂导汽管系统

本文以核电厂中导汽管道为工程背景［12］，对模型修正方法进行阐述。导汽管道系统由4 根φ168 ×14 的合金钢管构成，每根导汽管水平段长为5364mm，两端分别与气缸和主蒸汽管的汽门相连接。将水平导管划分为10 个单元、11个节点，且每个单元属性相同。为模拟模型中的误差，假设工况：④号单元为管道焊接处（图2），其刚度发生偏差降低40%；为对比修正前后的效果，在模态分析基础上对管道进行时程分析，计算在地震激励下管道结构的位移和速度情况。地震波由El-Centro 波改造而来如图3所示。

图2 有限元管道模型Fig.2 Finite element pipeline model

图3 地震波形时程曲线Fig.3 Seismic waveform time history curve

试验结果是从与分析模型具有相同自由度数量的模型中获得，这是一种理想情况。但在实际工程中，利用仪器测量得到的数据是有限的。因此，假设仅在管道单元中4、5、6、7、8 有平动自由度试验结果，利用Guyan缩聚技术对有限元模型进行模型缩减，实现自由度匹配。在进行模型修正过程中，不能利用Baruch 和Bar-Itzhack所提出的直接修正法。Baruch和Bar-Itzhack认为质量矩阵是准确的，但模型在进行Guyan 缩聚过程中MG＝TTMT缩聚后的质量矩阵有转换矩阵的参与，而转换矩阵构建过程中需要利用刚度矩阵进行构造引入了误差，使得转换矩阵是带有误差的。因此，在模型修正时将试验数据作为参考基准，去修正刚度矩阵才更为准确。

通过图4 对比同一节点不同情况下的动力学响应，发现有限元模拟（修正前）管道焊接处的节点位移与真实情况偏差较大，真实模型运用Guyan缩聚得到的结果优于有限元模拟，刚度矩阵修正后的结果最好，位移响应更贴合真实情况。通过图4 中不同节点下的响应情况，发现在节点6、7、8 处（材料属性无变化）模型修正前后的位移响应并无明显变化，Guyan 缩聚得到的结果与真实情况偏差最大。通过表3 最大位移可以观察到节点6、7、8 刚度矩阵修正后的误差反而大于修正前的结果，误差提升了1%左右。误差变大是Guyan缩聚转换矩阵所引起的。在材料属性损伤处，由原本的21%降低到2%左右。模型修正后的位移误差可以控制在2%左右，有限元模拟的结果在整体上的误差相对更大且很不稳定。