基于动态贝叶斯网络的钢桥检测和维修优化研究*

2022-07-14曾勇史振伟薛晓芳谭红梅

特种结构 2022年3期

曾勇史振伟薛晓芳谭红梅

1.重庆交通大学省部共建山区桥梁与隧道工程国家重点实验室 400074

2.重庆交通大学山区桥梁结构与材料教育部工程研究中心 400074

引言

钢桥承受重复荷载，可能会导致疲劳病害或疲劳失效。因此，需要在设计使用寿命期间对疲劳的某些关键细节进行检查，检测潜在的疲劳损伤，并为适当的维修行为提供有用的证据（如疲劳关键细节的裂纹长度）。另一方面，检测和与之相关的维修行为会产生费用，增加钢桥运营阶段的全寿命成本。由此可知，有效规划疲劳关键细节的检测和维修行为不仅对确保结构功能和安全至关重要，而且对控制钢桥运营阶段的全寿命也很重要。

从20 世纪90 年代开始，针对疲劳结构如何既保证结构的安全性，又使得运营阶段的全寿命成本最低，海内外学者相继提出了一些基于概率的结构养护优化方法。Kong［1］等通过使用计算机程序对退化结构进行生命周期分析（该程序考虑了各种作用对退化结构一组剖面的可靠性指标的影响），并考虑结构的全生命周期成本，建立了基于可靠性的框架模型，并给出了退化桥梁的数值算例，验证了该方法的有效性。Stewart［2］等利用钢筋混凝土结构腐蚀开裂可能性和开裂程度的概率信息，发展了一种预测寿命周期成本的技术，该技术根据裂缝开裂的可能性和程度，建立维修费用函数，并作为判断维修时机和维修费用的标准。Soliman［3］等提出了一种概率方法，通过整合检测和监测行动获得的信息，找到疲劳敏感结构的最佳管理计划，该方法利用依赖于时间的概率损坏准则，结合检查成本和失效成本来找到不确定情况下的最佳检测时间，在结构服役期间执行检测操作，所产生的新信息，将用于更新损伤传播参数和对结构的养护进行优化。Faber［4］等采用贝叶斯概率网络评估了某海上设施拆除的风险性，主要是利用贝叶斯概率网络进行敏感度分析，用于改进风险评估模型。J. Zhu［5］等通过积分提出了一种概率模型，使用动态贝叶斯网络进行现场检查，同时考虑相关的不确定性，用于正交异性钢桥面板的疲劳损伤的诊断和预测。

进入21 世纪以后，我国的一些学者也开始注意和研究此方向，并取得不错的成果。杨伟军［6］等基于桥梁运营阶段的动态可靠性，结合维修加固成本与加固完成后的经济效益，提出了一种以动态可靠性为约束，维修加固成本和失效损失之和为目标函数的决策方法。曾勇［7］等结合LEMF、结构可靠度理论和WLC 方法，提出了一种基于概率的钢桥焊接构件的疲劳养护策略优化方法，该方法以满足最小可靠度情况下总养护成本最低为准则，方法简单实用，可操作性强。黄天立［8］等采用伽马过程模拟钢桥的疲劳裂纹增长过程和疲劳失效概率，并结合检测概率和养护成本，以最大化构件使用寿命和最小化运营阶段养护成本为多目标函数，提出了基于伽马过程和遗传算法的钢桥构件疲劳裂纹检测和维护策略优化计算模型。

经上述研究现状发现，所采取的疲劳寿命评估方法的不足之处在于不能够获得疲劳裂纹的实际尺寸。当采用无损检查技术对钢桥进行检测时，不仅可以检测出结构的损害程度，更重要的是还能够获得疲劳裂纹的实际尺寸，而实际裂纹长度与采用各种方法模拟的裂纹长度往往会存在偏差。因此，本文采用动态贝叶斯网络，将无损检查获得的实际裂纹长度更新到基于动态贝叶斯网络的疲劳裂纹评估模型中，以保证各种方法模拟的实际裂纹长度的准确性。

1 钢桥检测和维修优化框架

虽然基于检测结果的后验分析能够更新疲劳裂纹评估模型并指导维修决策，但它对于选择检测计划（即无损检测技术）没有帮助。因此本文提出了一种综合性的基于概率的优化框架，用于选择疲劳关键细节的最佳检测和维修计划，拟议的框架如图1 所示。

图1 检测维修优化框架示意Fig.1 Schematic diagram of inspection and maintenance optimization framework

拟议的框架主要包括以下三个方面：

1.检测时间

在框架中用箭头表示钢桥的服役时间历程。检测时间可根据性能函数评估疲劳可靠性来确定，根据基于断裂力学理论的疲劳寿命评估模型进行预测，结合性能函数确定钢桥的第一次检测时间，然后将检测结果用动态贝叶斯网络更新钢桥疲劳细节的裂纹扩展模型，依据此模型确定下一次钢桥的检测时间，使用寿命期间剩余的检测也采用此方法。

2.检测维修事件树

确定检测以后，首先要根据疲劳细节、检测概率和基于动态贝叶斯网络的钢桥疲劳裂纹扩展模型等因素，从列举的检测方法I1～Ii中，选择出最佳的检测方法，检测完成后，根据获得的检测数据评估结构的损坏状态；最后再根据结构的损坏状态列举对应的维修措施R1～Ri。

3.养护决策流程图

首先要指定某一特定检测方法，根据检测获得的数据，利用动态贝叶斯网络的钢桥疲劳裂纹扩展模型评估钢桥的性能，列举维修措施，评估该维修措施下的钢桥性能，然后计算该措施的养护成本，循环计算不同维修措施下的养护成本，最终做出最佳的决策。

上述框架的关键之处在于如何将检测到的裂缝尺寸更新到结构的疲劳裂纹中去，并更新结构的性能。本文使用动态贝叶斯网络，将检测到的裂缝尺寸作为证据，用来达到上述目的。下面介绍一下动态贝叶斯网络模型的构建步骤，并建立基于动态贝叶斯网络的疲劳裂纹扩展模型。

2 动态贝叶斯网络模型的构建步骤

概率方法是解决不确定问题的一种相对有效的方式，而贝叶斯网络是将概率论统计应用于复杂领域、进行不确定性推理和数据分析的工具。目前动态贝叶斯网络在医疗诊断、工程应用、金融分析等领域有广泛的应用，是研究不确定性问题领域内发展较快的时变不确定信息推理技术。本文将动态贝叶斯网络的构建过程划分为以下四个阶段：

（1）获取变量阶段。贝叶斯网络中的特征变量是构建网络的基础，特征变量过多会导致计算量将呈量级增加，过少又会导致无法准确预测疲劳裂纹的扩展，构建的动态贝叶斯网络将失去意义。因此需要对研究的问题进行分析，确保能够得到与实际情况相符合的变量。在此阶段需要完成的工作有：确定节点变量及其状态分布，将其离散化处理，并确定变量的状态空间。

（2）构建静态贝叶斯网络。初始模型设计阶段即建立静态贝叶斯网络阶段，此阶段需要确定变量节点的拓扑结构和概率分布，然后使用Ge-

NIe软件完成静态贝叶斯网络的建模。

（3）构建动态贝叶斯网络。动态网络模型设计阶段的关键是确定随时间更新变化的节点，定义出转移网络。转移网络的定义有用引入算法进行定义的，也有利用专家知识进行定义的，可以根据研究问题具备的基础条件和需要进行选择。

（4）验证模型。可以通过输入工程实例数据进行正向推理，比较预测结果和使用最原始公式计算出来的数据的差距，来验证所构建的模型是否有效，如果结果差异较大，就需要对前面的步骤进行检查、修正。这一阶段是一个反复的过程。

2.1 获取动态贝叶斯网络模型变量

由于本文采用基于断裂力学的疲劳裂纹扩展模型对钢桥疲劳细节进行寿命评估，因此在本研究中，疲劳裂纹扩展由Paris公式（1）来确定：

式中：C、m为材料的疲劳参数；ΔK为循环应力强度因子，由循环应力引起；N为加载循环次数；Δa为一个时间段的裂纹扩展速率；Sre为等效应力幅；a0为当前时间段中的初始裂纹的长度；G为几何修正系数。

对于基于断裂力学的疲劳裂纹扩展模型，可以根据裂纹的长度定义疲劳的极限状态，当疲劳裂纹长度a达到预定阈值acr时，钢桥的构件达到其使用寿命。钢桥的极限疲劳状态可以通过式子（3）进行计算：

从式（3）可知，当E（t）＞0 时，构件处于安全状态；当E（t）＝0 时，构件处于临界状态；当E（t）＜0 时，构件处于危险状态。在此定义当疲劳裂纹长度a超过预定阈值acr时，构件处于危险状态，并将此事发生的概率命名为超限概率，并以Pf（t）来表示钢桥服役期t年时的超限概率。

从式（1）～（3）中可以得到贝叶斯网络的网络节点（节点变量）：材料常数C和m，循环应力强度因子ΔK，初始裂纹的长度a0，等效应力幅Sre，当前时间段的裂纹长度a，临界裂纹长度acr，当前时间段的疲劳状态E。

一般来说，贝叶斯网络的节点主要通过两种方式来获得变量空间：参数学习和专家咨询。由于监测资料少，搜集资料困难等原因，通过大样本数据进行参数学习的方法很难实现。另一方面，国内外学者对基于断裂力学的疲劳裂纹扩展拥有深入研究，对于本文涉及的变量，提出过针对不同材料和结构的概率分布。

2.2 构建静态贝叶斯网络模型

静态贝叶斯网络构建一般需要进行结构学习和参数学习，但是本文采用基于断裂力学的疲劳裂纹扩展模型，对于疲劳裂纹的计算有确定的公式，节点变量之间存在明显的逻辑关系，因此不需要进行结构学习和参数学习，下面根据疲劳裂纹的两种计算方式，提出两种静态贝叶斯网络。

1.方案一

根据公式（1）和（2）中的变量，建立了基于使用时间预测疲劳裂纹的增长模型，疲劳裂纹计算见公式（4）：

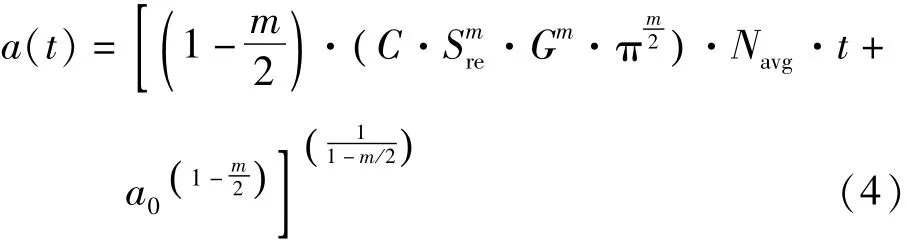
式中：t是服务年限；Navg是年平均负载周期数。

由于大多数检查结果与裂缝长度有关，因此，公式（4）基于裂缝的模型经常用于对裂缝寿命评估。

在该静态贝叶斯网络中，需要输入的节点参数包括Sre、G、C、m、N、t、a0，而at可以通过节点进行计算；裂纹的疲劳状态E，根据at进行确定。为了方便定义后续的节点变量，提出了两个中间变量，

2.方案二

根据公式（1）和（2）中变量及变量间的逻辑关系，使用GeNIe软件建立静态贝叶斯网络，如图2 所示。

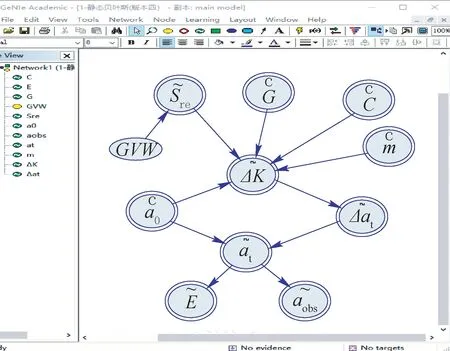
图2 方案二构建的静态贝叶斯网络Fig．2 Static Bayesian network constructed in scheme 2

在该静态贝叶斯网络中，GVW 表示汽车荷载，用于控制等效应力幅Sre；da／dN＝Δat表示一个时间段的裂纹扩展速率，并用于计算当前时间段的裂纹长度，at＝Δat＋a0；aobs表示通过无损检测观察到的实际裂纹长度，该值对于贝叶斯网络的更新起到重要的作用。裂纹的疲劳状态E，作用同方案一相同，用于获取当前时间段的疲劳细节超限概率Pf（t）。在此模型中需要输入Sre、G、C、m、GVW、a0，而aobs为观测值，在动态贝叶斯网络中才会起到作用。

为了模拟汽车荷载GVW 对疲劳构件应力幅的影响，通过建立ANSYS 有限元模型，输入汽车荷载，输出瞬态分析而获得的裂纹（即关键构件）处的应力时间历程。随后，基于Miner 的线性疲劳损伤累积理论，将计算的裂纹处的应力响应值，用于计算等效应力幅Sre。由于概率预测和贝叶斯推断都需要大量的ANSYS 模型，因此，该过程通常会略过，直接使用专家咨询方法对等效应力幅Sre进行定义。

3.对比分析

方案一和方案二都是基于断裂力学的疲劳裂纹扩展模型，两个方案都存在优缺点。方案一的优点是可以输入时间，计算任意时间的构件疲劳裂纹长度，有利于构建动态贝叶斯模型，缺点是输入的节点变量较多，计算较为复杂；方案二的优点是输入节点变量少，计算简单，缺点是模型中未存在关于时间的变量，构建动态贝叶斯网络时处理会较为复杂。因此，为方便构建动态贝叶斯网络模型和准确获取时间t的裂纹长度，本文使用方案一处理疲劳裂纹问题，并构建动态贝叶斯网络模型。

2.3 构建动态贝叶斯网络模型

当构建静态贝叶斯网络模型之后，下一步的工作就是构建动态贝叶斯网络。一般而言，从静态到动态需要定义出转移网络和转移概率。转移网络表示两个相邻静态贝叶斯网络的转移过程，包括结构转移和参数转移过程；转移概率表示节点状态在转移过程发生的概率变化。本文使用GeNIe软件直接通过公式（4）定义两个时间段之间的关系，以t－1 时间段的裂纹作为t时间段初始裂纹，t时间段的裂纹就可以通过公式进行计算，两个时间段之间的转移如图3 所示。当定义a3时间段的裂纹长度时，以a2作为a3时间段的初始裂纹长度，之后的时间段以此类推。由此可见，本文采用的方法是直接通过公式定义出转移网络。

图3 动态贝叶斯网络节点之间的关系转换Fig.3 Relationship transformation diagram between nodes of dynamic Bayesian network

在使用GeNIe建立动态贝叶斯网络时，首先要调出时间板，时间板调出之后，整个空间划分为四部分：时间板之外的部分表示节点处于同一时间，是静态的；时间板左侧的部分表示动态贝叶斯网络的初始状态，里面的节点类似于时间板外的静态节点，它们只能够连接到动态贝叶斯网络中的第一个时间段；时间板中间的部位是动态模型的主要表现部分，此处是唯一允许有时间弧的部位，同时还可以显示将要对其执行推断的时间段数；时间板右侧的部位是动态贝叶斯网络的最终状态，一般连接到网络最后一个时间段。本文在建立动态贝叶斯网络时，首先将静态贝叶斯网络的a0节点拖入时间板的左侧部分，a0节点作为初始状态定义完成后，将at节点和E节点拖入时间板的中间部分，并定义表示指向自身的时间弧。在本次操作中并未定义动态贝叶斯网络的最终状态，同时还可以从图中发现，构建的动态贝叶斯网络表示9 个时间段的内容。

GeNIe建立的动态贝叶斯网络一般存在两种形式。一种是未展开式，该形式网络结构简单，与静态贝叶斯网络类似，但是查询数据较为复杂，不方便使用。另一种是展开式，该形式网络结构稍微复杂，但是可以明显观察到各个时间段的节点情况，方便查询各个节点的数据。因展开式方便查询和修改数据，后续多采用此种方式的动态贝叶斯网络。值得注意的是，此处采用的动态贝叶斯网络仅对初始裂纹和年平均应力循环次数这两个参数进行更新，而实际情况往往并非如此，如交通量会发生变动。

2.4 模型验证

从前面介绍可知，本文中的动态贝叶斯网络是基于公式（4）构建的，而基于断裂力学的疲劳裂纹扩展最典型的公式是Paris 公式，使用Paris公式计算的数值具有一定的可信度。因此，本文使用Paris公式来验证动态贝叶斯网络模型计算的正确性。

当考虑节点变量的取值问题时，如果选取的节点变量含有概率的情况，如正态分布、指数正态分布等，那么使用Paris 公式计算的裂纹长度也会包含不确定性，这会使得模型的验证变得较为复杂，验证的效果也会不理想。所以，本文验证时不考虑概率的因素，选取的节点变量均为定值。

以某钢桥桥面板纵向加劲肋为例，初始裂纹长度a0取为0.1mm，等效应力幅Sre取32MPa，假设疲劳发生位置函数G为1.0，其余动态贝叶斯网络中的节点变量取值如表1 所示。

表1 动态贝叶斯网络中的节点变量取值Tab.1 Node variable values in dynamic Bayesian Networks

采用表1 中的数据，根据Paris 公式，使用MATLAB软件，得到疲劳裂纹长度与疲劳细节服役期之间的关系曲线；另外，在动态贝叶斯网络模型中输入对应的时间t，得到疲劳裂纹长度与疲劳细节服役期之间的关系曲线，具体曲线图如图4 所示。

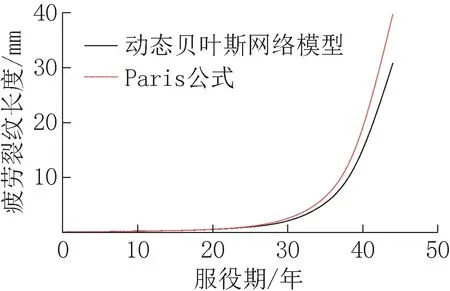
图4 疲劳裂纹发展曲线对比Fig.4 Comparison of fatigue crack growth curves

从图4 中可以看出，当不考虑疲劳细节使用过程中不确定性因素的影响时，基于Paris 公式绘制的图形是一条光滑的曲线，使用基于动态贝叶斯网络模型绘制的也是一条曲线，两曲线的增长趋势趋于一致。另外还可以从图4 中发现，疲劳细节自正常使用开始至服役期30 年，疲劳裂纹的扩展速度较为缓慢，两条曲线的值也较为接近；自服役期30 年后，疲劳裂纹的扩展速度迅速增长，两条曲线的值开始出现偏差，随着时间的增大，两条曲线的差值也慢慢变大；当裂纹扩展速度较为缓慢时，使用动态贝叶斯网络模型计算的值较为准确；当裂纹扩展速度较为迅速时，使用动态贝叶斯网络模型计算的值与Paris 公式计算的值会存在偏差，但偏差并不会太大，在可接受的范围内。

2.5 精确节点变量概率分布问题

在2.4 节中已经验证了节点变量取确定值时动态贝叶斯网络模型与Paris 公式计算的值较为接近，但在通常情况下，本文所涉及的节点变量不取确定值，而是以概率的形式来表示，如正态分布、对数正态分布和指数分布等。如何使用GeNIe软件较为准确的模拟节点变量的概率分布以及如何将节点变量的概率分布更准确的应用到动态贝叶斯网络是一个问题，接下来通过采样数和离散化两个方面来进行说明。

1.采样数

采样数是采样算法每次执行时设置使用的采样数目，所有的采样算法都是近似的。一般来说，样本的数量决定了结果的精度，采样时选取更多的样本，会有更精确的结果。另一方面，样本的数量与运算时间几乎是线性相关的，样本的数量越多，计算的时间越久。虽然采样数越多可以获得较为准确的精度，但当达到一定的采样数以后，获得的结果已经较为满意，继续增加样本数只会增加计算量，并不会提高结果的精度。因此，应该选择出一种合理的采样数，既能保证计算的精度又可以减小计算量。

在对概率问题进行研究时发现，当事件X服从正态分布N（μ，σ2）时，P（μ －σ ＜X≤μ ＋σ）＝0.6826，P（μ －2σ ＜X≤μ ＋2σ）＝0.9544，P（μ－3σ ＜X≤μ ＋3σ）＝0.9974。可以看出事件X服从正态分布时，特定范围的概率值为确定值，刚好可以用来验证采样数对精度的影响。在此假设某节点S服从正态分布N（30，22），分别观察5000 采样数、10000 采样数、100000 采样数、500000 采样数时处于μ ±σ、μ ±2σ 和μ ±3σ范围内的样本数，不同采样数在特定范围内的样本数和概率如表2 所示。不同采样数在特定范围内的概率值如图5 所示。

表2 不同采样数在特定范围内的样本数和概率Tab.2 Sample number and probability of different sample numbers in a specific range

从图5 宏观角度来看，选取的的四组采样数在特定范围内的概率值与标准值相差几乎不大，这表明GeNIe软件在进行随机采样时具有较高的准确度；另一方面，从表2 微观角度来看，当采样数为5000 样本和10000 样本时，采样数在特定范围内的概率值与标准值还是存在一定的偏差。当采样数为10000 样本和500000 样本时，采样数在特定范围内的概率值与标准值较为接近。而从数据上来看，当采样数为100000 时，取值与标准值相差很小，完全能够满足计算要求。因此，本文在使用动态贝叶斯网络模型进行计算时，为了避免不必要的计算和保证计算结果的精度，选取的采样数为100000。

图5 不同采样数在特定范围内的概率Fig.5 Probability values of different sampling numbers in a specific range

2.离散化

在前面提到，本文所涉及的节点变量较多的是以概率的形式来表示，如正态分布、对数正态分布和指数分布等，而这些概率分布都是连续性分布。当节点为连续性分布时，没有普遍可靠的随机抽样算法。在这种情况下，GeNIe 软件提出了一种自动离散化的算法。该算法将原始的基于方程的连续网络转化为离散贝叶斯网络，而原始的网络定义没有改变，但是在使用动态贝叶斯网络推理时是在一个临时的离散贝叶斯网络中进行的，这个网络专门为推理而创建。为了使用该算法，需要用离散化的规范来增强网络中节点的定义，如果不这样做，GeNIe 软件会本着保持每个模型语法正确性的精神，将每个变量离散成两种状态，在大多数情况下，两种状态不足以满足要求，应该重新访问有问题的节点，将它们离散成更多的间隔。

当进行离散化操作之前，首先需要定义节点变量取值的上下限。对于正态分布，由于3σ 原则，在（μ －3σ，μ ＋3σ）以外的取值概率不到0.3%，几乎不可能发生。所以，上限可取μ －3σ，下限可取μ ＋3σ。对于对数正态分布或其概率分布，可先不定义上下限，离散化查看结果取值之后，再结合实际情况重新定义节点变量的上下限。在此以某节点S服从正态分布N（30，22）为例，上限取24，下限取36，离散状态取10个，使用GeNIe 软件自动离散化后的结果如图6所示。

图6 自动离散化后的结果Fig.6 Results of automatic discretization

在进行离散化时需要考虑将节点变量离散为多少状态。以疲劳裂纹为例，如果离散的状态数目较少，会使得裂纹在扩展过程中一直处于某个状态不变，显然这不利于我们的分析，而如果离散的状态数目较多，会出现40 ～60 个状态，这虽然会使得结果更加精确，但会大大的增加统计数据工作的难度。所以，要根据实际情况来确定离散的状态数目。