基于GA-SVM的GNSS高程拟合应用研究

2022-07-14方云波

河南科技 2022年12期

方云波

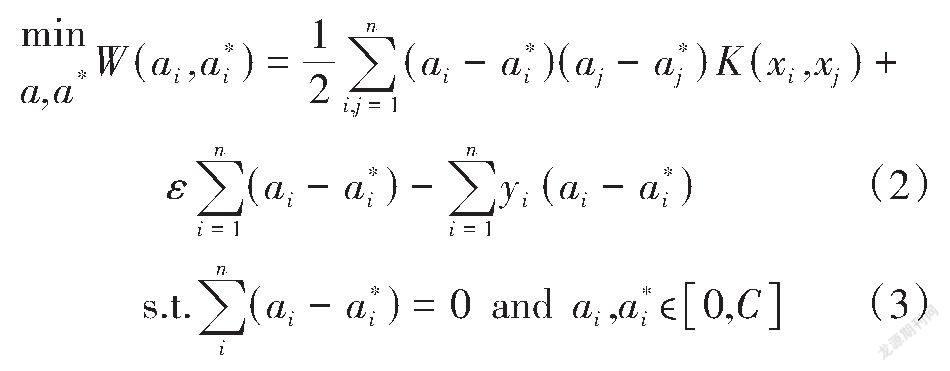
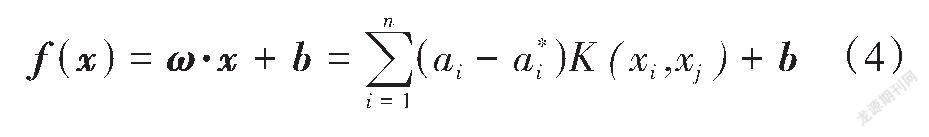
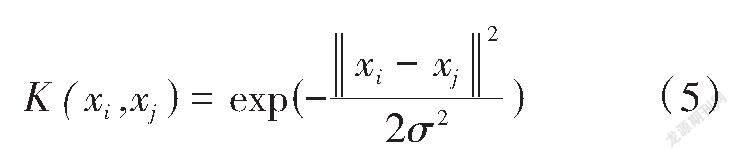
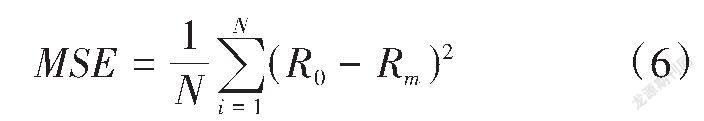
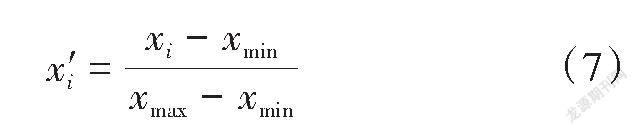
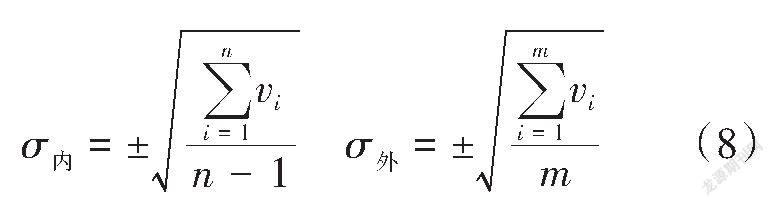
摘要：在支持向量机GNSS高程拟合应用中，通常采用交叉验证法来寻找训练模型的最优参数，但该方法有可能会陷入局部最优而难以提高模型精度。本研究采用具有全局寻优能力的遗传算法来优化支持向量机的参数，并建立GA-SVM模型对GNSS高程数据进行拟合。通过对比交叉验证表明，GA-SVM在GNSS高程拟合中具有更好的效果，内符合精度和外符合精度均达到毫米级。

关键词：遗传算法;支持向量机;高程拟合;交叉验证

中图分类号：P228 文献标志码：A 文章编号：1003-5168（2022）12-0013-04

DOI：10.19968/j.cnki.hnkj.1003-5168.2022.12.002

Application Research of GNSS Height Fitting Based on GA-SVM

FANG Yunbo

（Shanghai Weichen Surveying and Mapping Technology Co.，Ltd.，Shanghai 200100，China）

Abstract：In the application of support vector machine GNSS height fitting，the cross-validation method is usually used to find the optimal parameters of the training model.This method may fall into local optimization and is difficult to improve the accuracy of the model.In this paper，a genetic algorithm with global optimization ability is used to optimize the parameters of the support vector machine.GA-SVM model is established to fit GNSS height data.Compared with the cross-validation method，GA-SVM has a better effect on GNSS height fitting.The internal coincidence accuracy and external coincidence accuracy reach the millimetre level.

Keywords：genetic algorithm;support vector machine;height fitting;cross-validation

0 引言

GNSS技术能够获取点位的三维坐标，从而广泛应用于大地测量和工程测量领域。但由于GNSS所测的高程为大地高，几何水准测量获取的是正常高，大地高是空间点沿法线到参考椭球面的距离，正常高则是空间点沿铅垂线到似大地水准面的距离，两个高程之间存在高程异常，导致GNSS测得的高程不能被直接使用，从而浪费了大量的观测数据。几何水准测量是目前精度最高的方法，但施测效率却很低，需要花费大量的人力和时间，测量成本较高[1]。因此，研究GNSS大地高与水准测量正常高之间的高程转换方法对提高高程测量效率具有重要意义。对于局部工程区域，目前常用的测量方法有等值线图法、多项式拟合法、多面函数法等，但这些方法都要采用事先假设的函数模型来进行高程异常拟合，而拟合效率的优劣则取决于所选的函数模型。因此，不可避免地存在模型误差。

支持向量机（Support Vector Machine，SVM）是在统计学理论基础上建立起的一种机器学习算法[2]，由于其遵循结构风险最小化原则及善于处理小样本问题的能力，逐渐被应用于GNSS高程拟合中[3-6]。SVM性能的好坏取决于其模型参数，一般是基于交叉验证（Cross-Validation，CV）算法求得，但该算法有时会陷入局部最优解，难以找到全局最优参数。而遗传算法（Genetic Algorithm，GA）是一种模仿自然界中生物遗传机制和进化机制演变而来的寻优算法，能够得到全局最优状态[7]。因此，本研究建立基于遗传算法的支持向量机（GA-SVM）模型，将该模型应用于GNSS高程拟合中，通过对比交叉验证，来验证该模型的拟合效果和模型精度。

1 SVM模型

SVM是基于统计学习理论的一种通用机器学习算法，由Vapnik等人于1995年提出，是机器学习领域的标准工具之一[8]。SVM模型以结构风险最小化原则来平衡模型的复杂性和学习能力，通过求解高维空间线性约束的二次规划问题从而得到全局最优解[9]。

SVM模型源于线性回归问题，见式（1）。

[f（x）=ω·x+b] （1）

根据向量[（xi， f（xi））]，[i=1，2，...，n]来构建拟合模型，其中[xiϵRn]作为输入，[f（xi）ϵR]作为输出，目标是求出[ω]和b。

对于非线性问题，最省力的方法是利用式（1）的线性方法来解决，采用非线性映射[ϕ]，将输入空间的向量x映射到高维的Hilbert空间，转换为高维向量[ϕ]（x），这样输入空间中的非线性问题就会转换为高维特征空间中的廣义线性问题，从而可以在高维空间中进行线性回归[10]。

值得注意的是，虽然非线性映射能够在高维特征空间中解决非线性拟合问题，但这个非线性映射函数[ϕ]却不容易被找到，故针对不同的实际问题直接采用非线性映射是不易实现的。但是，非线性映射可通过内积运算来完成，因此，可通过核函数来代替非线性映射的内积运算，则高维特征空间中回归问题可表达为式（2）和式（3）。

式中：[ε]为损失参数，影响支持向量的数量;C为惩罚参数，其是对错分样本进行控制，以实现在错分样本的比例和算法的复杂程度之间“折中”的目的;[K（xi，xj）]为核函数，可以看出核函数是计算的捷径，避免了非线性函数[ϕ]的寻找和复杂的内积运算[11]。

进而得到线性回归函数，见式（4）。

由于高斯核函数具有普适性，适用于各分布类型的样本[12]。因此，本研究采用的高斯核函数见式（5）。

式中：[σ]为高斯核参数，SVM的3个参数损失参数[ε]、惩罚参数C和核函数参数[σ]的合理选取是SVM建模的关键。

2 CV-SVM模型

CV-SVM模型采用交叉验证法来优化SVM的参数，其基本思想是设置参数遍历区间，对原始数据进行分组，一部分作为训练集，另一部分作为验证集，先用SVM模型对训练集进行训练，再利用验证集来测试模型的优劣，不断进行试算，以此作为SVM的性能指标，直至找到最优的参数。常用的交叉验证法有留出法、K-折交叉法和留一法。

留出法是将原始数据随机分成两组，一组作为训练集，另一组作为验证集。利用SVM模型进行训练，利用验证集对模型精度进行验证，从而选择模型参数。该方法分组简单且运算效率高，但并没有执行严格意义上的交叉验证，故难以提高精度。

K-折交叉验证法是将原始数据均匀地分成K组，从而生成K个子集，将每个子集分别作为一次验证集，其余子集则作为训练集，逐组进行训练和验证。该方法可有效避免过学习和欠学习状态，其验证精度较高。

留一法是指每次只留一个样本作为验证集，其余样本均为训练集，直至遍历组合全部样本。该方法每次交叉验证基本会将所有样本用于训练，更加接近原始样本的分布状态，使得验证结果比较可靠，但运算量非常大，计算耗时且成本高，难以在实际问题中应用。综合考虑，本研究采用K-折交叉验证方法来进行SVM训练建模。

3 GA-SVM模型

遗传算法是借鉴自然界中生物遗传和进化机制，通过选择、交叉、变异等遗传操作，产生新的种群，以此不断迭代，最终得到最优的后代，从而达到获取全局最优解的效果。GA-SVM模型是利用遗传算法获取全局最优解来对支持向量机模型参数进行优化，算法流程如下。

3.1 参数编码

为了使计算的参数能够尽可能接近最优解，在设置SVM核参数时，尽量增大搜索空间。设置惩罚参数C的寻优区间为（0，100]，损失参数ε的寻优区间为[0，1]，核参数的倒数[1/σ]的寻优区间为[0，1 000]。对上述3个SVM参数进行二进制编码，生成一组代表这3个参数的染色体作为初始种群。如ε的编码方式为A，C的编码方式为B，[1/σ]的编码方式为C，则个体的编码形式为[A，B，C]。

3.2 适应度函数的选择

适应度函数是遗传算法和支持向量机算法之间的“纽带”，种群个体对环境适应能力的数学表达与目标函数有关。本研究的目的是对GNSS高程异常进行拟合，因此，选用拟合结果的均方误差作为目标函数，见式（6）。

式中：MSE为均方误差;R0为实测值;Rm为拟合值;N为拟合样本数。

3.3 遗传操作

3.3.1 选择。选取种群中生命力强（适应度大）的个体，使其交叉变异进化到下一代，同时淘汰适应度低的个体，以保证种群向着适应环境的方向进化。本研究根据适应度函数，选取轮盘赌法对种群个体进行选择。

3.3.2 交叉。种群中会不断产生新的个体，要对搜索空间中的新区域进行搜索，为了防止陷入局部最优，本研究采用单点交叉的方式。

3.3.3 变异。对个体染色体编码串中的某些基因座上的基因值取反（在二进制编码中，“0”与“1”互为反值），从而形成新的个体，其决定了遗传算法的局部搜索能力，维持群体的多样性，防止出现“早熟”现象。

3.4 遗传终止

采用预先设定的代数（终止迭代的次数）作为算法的终止条件，本研究设定的最大代数为200。当种群最优个体适应度达到某一阈值或迭代达到最大代数后，算法终止，经过解码得到SVM模型的最优参数。

4 基于GA-SVM的GNSS高程拟合案例分析

选取某地形平缓区域的B级GNSS控制网为研究对象，控制网中具有17个无粗差且精度相同的水准联测控制点，点间平均边长约为1 km，控制网区域面积约为10 km2，点位分布如图1所示，横轴和纵轴分别为高斯平面直角坐标系统的Y轴和X轴，三角形点为训练集中的控制点，圆形点为检核集中的控制点。

根据各控制点的正常高和大地高来计算高程的异常值，以控制网中12个控制点归一化后的坐标和大地高作为训练集的输入集，高程异常值作为训练集的输出集，进行SVM参数训练，其余5个点作为检核集来检验SVM模型的精度。归一化处理方法见式（7）。

式中：[x'i]为归一化后的数据;[xi]为归一化前的原始数据;[xmax]和[xmin]分别为归一化之前数据的最大值和最小值。归一化处理是一种无量纲处理算法，能够避免因数据之间的量纲差异过大而淹没了小量纲数据。

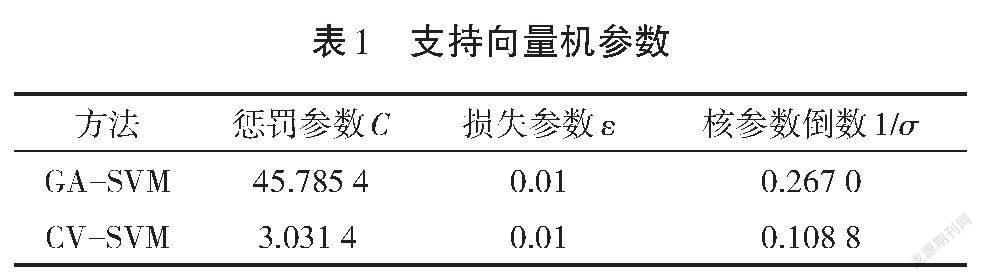
分别采用GA-SVM和CV-SVM方法对参数进行寻优，得到最终优化参数，结果如表1所示。

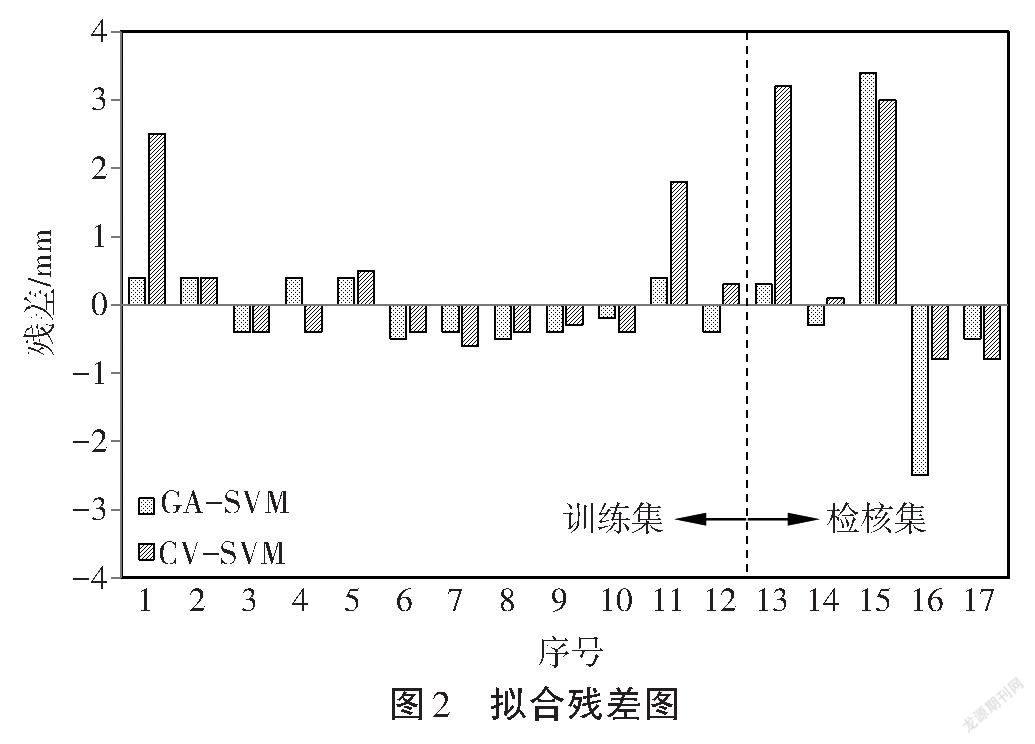
利用表1中的支持向量机参数进行GNSS高程拟合，GA-SVM和CV-SVM两种方法拟合结果的残差如图2所示，横坐标为控制点编号，纵坐標为拟合残差，虚线为训练集和检核集的分界线，虚线左侧为训练集，共12个控制点，虚线右侧为检核集，共5个控制点。

采用公式（8）对训练集和检核集的拟合精度进行内符合精度和外符合精度评定，精度评定结果如表2所示。

式中：[σ内]为内符合精度;[σ外]为外符合精度;vi为拟合残差值;n为训练集中控制点的个数;m为检核集中控制点的个数。

从图2可以看出，对于训练集，GA-SVM模型中的1号点和11号点的拟合残差明显较CV-SVM模型的小，且GA-SVM模型12个点中有7个点的拟合残差小于CV-SVM模型，其余5个点的差别不大，故GA-SVM训练集的精度高于CV-SVM。对于检核集，两种模型的拟合残差有大有小，整体精度在图中不易比较，但由表2可以看出，无论是内符合精度还是外符合精度，GA-SVM模型均优于CV-SVM模型，并且精度提高了一倍。整体试验结果表明，CV-SVM模型和GA-SVM模型在GNSS高程拟合中都能够达到毫米级的精度，GA-SVM模型能够寻找到比CV-SVM模型更优的参数，体现出遗传算法的全局最优解特性。因此，支持向量机是一种较为理想的GNSS高程拟合算法。

5 结论

支持向量机是一种能够解决小样本机器学习的有效算法，其以结构风险最小化的理念在模型的复杂性和学习能力之间寻求平衡，具有很好的训练和泛化能力。遗传算法是一种全局寻优算法，可以得到全局最优解。本研究将遗传算法应用于支持向量机模型的惩罚参数、损失参数和核函数参数的寻优中，建立了基于遗传算法的支持向量机模型，应用于有限控制点数量的GNSS高程拟合中，并与常规的交叉验证法进行比较，得到以下结论。

①交叉验证法和遗传算法支持向量机模型在GNSS高程拟合中都能够达到毫米级精度，说明支持向量机具备很好的训练和泛化能力，适用于GNSS高程拟合工作。

②支持向量机参数决定了模型的性能，遗传算法支持向量机模型能够解决交叉验证算法可能陷入局部最优的问题，能够寻找到更优的参数，拟合精度比交叉验证法提高了一倍。

参考文献：

[1] 朱春宁，王成，唐佑辉，等.GPS高程拟合模型选取及实验分析[J].勘察科学技术，2014（6）：21-23，42.

[2] 丛康林，岳建平.基于SVR的GPS高程拟合模型研究[J].测绘通报，2011（2）：8-11.

[3] 黄磊，张书毕，王亮亮，等.粒子群最小二乘支持向量机在GPS高程拟合中的应用[J].测绘科学，2010（5）：190-192.

[4] 吕亚军，王亚军，鹿先锋，等.GPS高程拟合支持向量机模型[J].全球定位系统，2009（3）：11-13.

[5] 任超，李和旺.最小二乘支持向量机在GPS高程拟合中的应用[J].工程勘察，2012（7）：55-57.

[6] 朱华，赵仲荣，黄张裕，等.最小二乘支持向量机在GPS高程拟合中的应用研究[J].勘察科学技术，2013（6）：47-49.

[7] 刘钰.基于遗传算法的支持向量机在空气质量评價中的应用[D].大连：东北财经大学，2013.

[8] 夏铭泽.基于改进支持向量机的产品质量预测系统的研究[D].北京：机械科学研究总院，2020.

[9] 邓乃扬，田英杰.数据挖掘中的新方法：支持向量机[M].北京：科学出版社，2004