领悟概念本质 巧解难点问题

杨春猛

(云南省玉溪市红塔区教育科学研究所,653100)

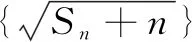
一、解法探究

1.运用等差数列通项公式和前n项和公式

2.运用特殊与一般的数学思想

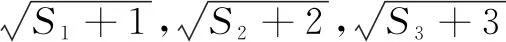
3.利用公差不为0的等差数列是特殊的一次函数的本质特性

二、方法比较

以上三种方法都能解决这一个问题,前两种方法对学生在概念本质上的要求相对较低,对学生的运算求解能力和观察能力要求较高,第三种方法对学生的运算求解能力和观察能力要求相对较低,而对“公差不为0的等差数列是特殊的一次函数”这一本质的理解要求较高．

三、第三种方法的巧用

例2(2021年全国甲卷理科数列问题)已知数列{an}的各项均为正数,记Sn为{an}的前n项和,从下面① ② ③ 中选取两个作为条件,证明另外一个成立.

注:若选择不同的组合分别解答,则按第一个解答计分.

这里只选① ② 作条件证明③,利用“公差不为0的等差数列是特殊的一次函数”这一本质属性解决该问题,不再赘述高考的标准答案和其他的方法．

不难看出,在高考评价体系下,基于学科核心素养的考查要求,对学生“真真正正明白数学概念和命题”提出更高的要求，在解题教学中应多加关注．